AI笔记: 数学基础之方向导数的计算和梯度

方向导数

定理

若函数f(x,y,z)在点P(x,y,z)处可微，沿任意方向l的方向导数
∂f∂l=∂f∂xcosα+∂f∂ycosβ+∂f∂zcosγ\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} cos \alpha + \frac{\partial f}{\partial y} cos \beta + \frac{\partial f}{\partial z} cos \gamma∂l∂f=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ
其中α,β,γ\alpha, \beta, \gammaα,β,γ 为l的方向角
证明
- 由函数f(x,y,z)f(x,y,z)f(x,y,z)在点P可微
- △f=∂f∂x△x+∂f∂y△y+∂f∂z△z+o(ρ)\triangle f = \frac{\partial f}{\partial x} \triangle x + \frac{\partial f}{\partial y} \triangle y + \frac{\partial f}{\partial z} \triangle z + o(\rho)△f=∂x∂f△x+∂y∂f△y+∂z∂f△z+o(ρ)
- =ρ(∂f∂xcosα+∂f∂ycosβ+∂f∂zcosγ)+o(ρ)= \rho(\frac{\partial f}{\partial x} cos \alpha + \frac{\partial f}{\partial y} cos \beta + \frac{\partial f}{\partial z} cos \gamma) + o(\rho)=ρ(∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ)+o(ρ)
- ∂f∂l=lim⁡ρ→0△fρ=∂f∂xcosα+∂f∂ycosβ+∂f∂zcosγ\frac{\partial f}{\partial l} = \lim_{\rho \to 0} \frac{\triangle f}{\rho} = \frac{\partial f}{\partial x} cos \alpha + \frac{\partial f}{\partial y} cos \beta + \frac{\partial f}{\partial z} cos \gamma∂l∂f=limρ→0ρ△f=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ

备注：图片托管于github，请确保网络的可访问性

对于二元函数f(x,y)在点P(x,y)处沿着方向l(方向角为α,β\alpha, \betaα,β)的方向导数为
∂f∂l=lim⁡ρ→0f(x+△x,y+△y)−f(x,y)ρ=fx′(x,y)cosα+fy′(x,y)cosβ\frac{\partial f}{\partial l} = \lim_{\rho \to 0} \frac{f(x+\triangle x, y + \triangle y) - f(x,y)}{\rho} = f_x'(x,y)cos \alpha + f_y'(x,y) cos \beta∂l∂f=limρ→0ρf(x+△x,y+△y)−f(x,y)=fx′(x,y)cosα+fy′(x,y)cosβ
- ρ=(△x)2+(△y)2\rho = \sqrt{(\triangle x)^2 + (\triangle y)^2}ρ=(△x)2+(△y)2
- △x=ρcosα\triangle x = \rho cos \alpha△x=ρcosα
- △y=ρcosβ\triangle y = \rho cos \beta△y=ρcosβ
特别地
- l与x轴同向(α=0,β=π2\alpha = 0, \beta = \frac{\pi}{2}α=0,β=2π)时，有∂f∂l=∂f∂x\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x}∂l∂f=∂x∂f
- l与x轴反向(α=π,β=π2\alpha = \pi, \beta = \frac{\pi}{2}α=π,β=2π)时，有∂f∂l=−∂f∂x\frac{\partial f}{\partial l} = -\frac{\partial f}{\partial x}∂l∂f=−∂x∂f

备注：图片托管于github，请确保网络的可访问性

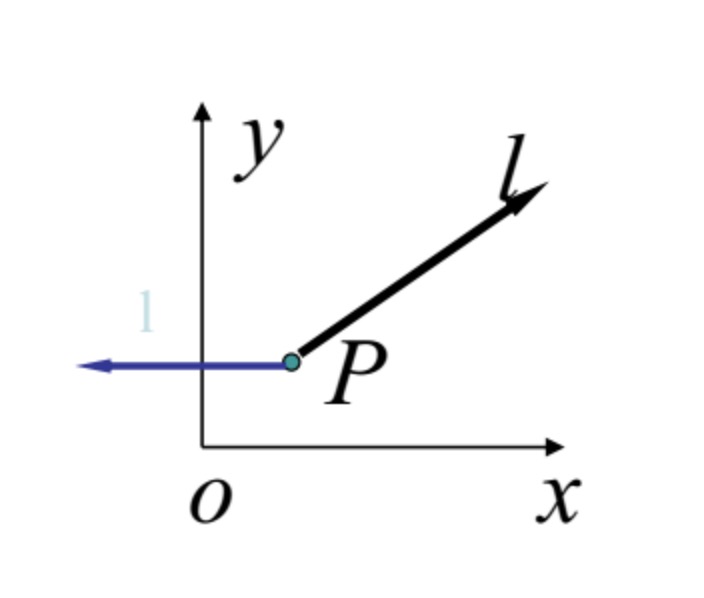
方向导数

方向导数(directional derivative): 有时不仅仅需要知道函数在坐标轴上的变化率(即偏导数)，还需要设法求得函数在其他特定方向上的变化率；
而方向导数就是函数在其他特定方向上的变化率。
如果函数z=f(x,y)z=f(x,y)z=f(x,y)在点P(x,y)是可微分的，那么，函数在该点沿着任意方向L的方向导数都存在
且计算公式为：∂f∂l=∂f∂xcosα+∂f∂ycosβ\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} cos \alpha + \frac{\partial f}{\partial y} cos \beta∂l∂f=∂x∂fcosα+∂y∂fcosβ

备注：图片托管于github，请确保网络的可访问性

例1

求函数u=x2yzu = x^2yzu=x2yz 在点P(1,1,1)沿向量 l⃗=(2,−1,3)\vec{l} = (2, -1, 3)l=(2,−1,3)的方向导数.
∂u∂l=∂u∂xcosα+∂u∂ycosβ+∂u∂zcosγ\frac{\partial u}{\partial l} = \frac{\partial u}{\partial x} cos \alpha + \frac{\partial u}{\partial y} cos \beta + \frac{\partial u}{\partial z} cos \gamma∂l∂u=∂x∂ucosα+∂y∂ucosβ+∂z∂ucosγ
解
- 向量l⃗\vec{l}l的方向余弦为: cosα=214,cos⁡β=−114,cosγ=314cos \alpha = \frac{2}{\sqrt{14}}, \cos \beta = \frac{-1}{\sqrt{14}}, cos \gamma = \frac{3}{\sqrt{14}}cosα=142,cosβ=14−1,cosγ=143
- ∂u∂l∣P=(2xyz∗214)−x2z∗114+x2y∗314∣(1,1,1)=614\left. \frac{\partial u}{\partial l} \right|_P = \left. (2xyz * \frac{2}{\sqrt{14}}) - x^2z * \frac{1}{\sqrt{14}} + x^2y * \frac{3}{\sqrt{14}} \right|_{(1,1,1)} = \frac{6}{\sqrt{14}}∂l∂u∣∣P=(2xyz∗142)−x2z∗141+x2y∗143∣∣∣(1,1,1)=146

例2

求函数z=xe2yz=xe^{2y}z=xe2y在点P(1,0)处沿从点P(1,0)到点Q(2, -1)的方向的方向导数
解
- 方向l即向量PQ=(1,−1)PQ = (1, -1)PQ=(1,−1)的方向，与l同方向的单位向量el=(12,−12).=(cosα,cosβ)e_l = (\frac{1}{\sqrt{2}}, - \frac{1}{\sqrt{2}}). = (cos \alpha, cos \beta)el=(21,−21).=(cosα,cosβ)
- 因函数可微，且∂z∂x∣(1,0)=e2y∣(1,0)=1,∂z∂y∣(1,0)=2xe2y∣(1,0)=2\left. \frac{\partial z}{\partial x} \right|_{(1,0)} = \left. e^{2y} \right|_{(1,0)} = 1, \left. \frac{\partial z}{\partial y} \right|_{(1,0)} = \left. 2xe^{2y} \right|_{(1,0)} = 2∂x∂z∣∣(1,0)=e2y∣∣(1,0)=1,∂y∂z∣∣∣(1,0)=2xe2y∣∣(1,0)=2
- 所以，所求方向导数为：∂z∂l∣(1,0)=1∗12+2∗(−12)=−22\left. \frac{\partial z}{\partial l} \right|_{(1,0)} = 1 * \frac{1}{\sqrt{2}} + 2 * (- \frac{1}{\sqrt{2}}) = - \frac{\sqrt{2}}{2}∂l∂z∣∣(1,0)=1∗21+2∗(−21)=−22

例3

求f(x,y,z)=xy+yz+zxf(x,y,z) = xy + yz + zxf(x,y,z)=xy+yz+zx 在点(1,1,2)沿方向l的方向导数，其中l的方向角分别为：60°, 45°, 60°
解：
- 与l同方向的单位向量 el=(cos60°,cos45°,cos60°)=(12,22,12)e_l = (cos 60°, cos 45°, cos 60°) = (\frac{1}{2}, \frac{\sqrt{2}}{2}, \frac{1}{2})el=(cos60°,cos45°,cos60°)=(21,22,21)
- 因函数可微，且
  - fx′(1,1,2)=(y+z)∣(1,1,2)=3f_x'(1,1,2) = (y + z)|_{(1,1,2)} = 3fx′(1,1,2)=(y+z)∣(1,1,2)=3
  - fy′(1,1,2)=(x+z)∣(1,1,2)=3f_y'(1,1,2) = (x + z)|_{(1,1,2)} = 3fy′(1,1,2)=(x+z)∣(1,1,2)=3
  - fz′(1,1,2)=(y+x)∣(1,1,2)=2f_z'(1,1,2) = (y + x)|_{(1,1,2)} = 2fz′(1,1,2)=(y+x)∣(1,1,2)=2
- 所以∂f∂l∣(1,1,2)=3∗12+3∗22+2∗12=12(5+32)\frac{\partial f}{\partial l} |_{(1,1,2)} = 3*\frac{1}{2} + 3*\frac{\sqrt{2}}{2} + 2*\frac{1}{2} = \frac{1}{2}(5 + 3\sqrt{2})∂l∂f∣(1,1,2)=3∗21+3∗22+2∗21=21(5+32)

梯度

1 ）概念

在空间的每一个点都可以确定无限多个方向，因此，一个多元函数在某个点也必然有无限多个方向导数.
在这无限多个方向导数中，最大的一个(它直接反映了函数在这个点的变化率的数量级)等于多少? 它是沿什么方向达到的?
描述这个最大方向导数及其所沿方向的矢量，就是我们所讨论的梯度.
梯度是场论里的一个基本概念.所谓"场", 它表示空间区域上某种物理量的一种分布
从数学上看，这种分布常常表示为 Ω\OmegaΩ 上的一种数值函数或向量函数
能表示为数值函数u=u(x,y,z)的场，称为数量场，如温度场、密度场等

2 ) 方向导数公式

∂f∂l=∂f∂xcosα+∂f∂ycosβ+∂f∂zcosγ\frac{\partial f}{\partial l} = \frac{\partial f}{\partial x} cos \alpha + \frac{\partial f}{\partial y} cos \beta + \frac{\partial f}{\partial z} cos \gamma∂l∂f=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ
- 令向量 G⃗=(∂f∂x,∂f∂y,∂f∂z)\vec{G} = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z})G=(∂x∂f,∂y∂f,∂z∂f)
- l°⃗=(cosα,cosβ,cosγ)\vec{l°} = (cos \alpha, cos \beta, cos \gamma)l°=(cosα,cosβ,cosγ)
∂f∂l=G⃗⋅l°⃗=∣G⃗∣cos(G⃗,l°⃗)(∣l°⃗∣=1)\frac{\partial f}{\partial l} = \vec{G}·\vec{l°} = |\vec{G}|cos(\vec{G}, \vec{l°}) \ \ \ (|\vec{l°}| = 1)∂l∂f=G⋅l°=∣G∣cos(G,l°) (∣l°∣=1)
当l°⃗\vec{l°}l°与G⃗\vec{G}G方向一致时，方向导数取最大值：max(∂f∂l)=∣G⃗∣max(\frac{\partial f}{\partial l}) = |\vec{G}|max(∂l∂f)=∣G∣
可见：G⃗\vec{G}G
- 方向：f 变化率最大的方向
- 模：f 的最大变化率之值

3 ) 梯度定义

向量G⃗\vec{G}G：称为函数f(P)f(P)f(P)在点P处的梯度(gradient), 记做：grad f
即 gradf=(∂f∂x,∂f∂y,∂f∂z)=∂f∂xi⃗+∂f∂yj⃗+∂f∂zk⃗grad \ f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z}\vec{k}grad f=(∂x∂f,∂y∂f,∂z∂f)=∂x∂fi+∂y∂fj+∂z∂fk
同样可定义二元函数f(x,y)在点P(x,y)处的梯度 gradf=∂f∂xi⃗+∂f∂yj⃗=(∂f∂x,∂f∂y)grad \ f = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})grad f=∂x∂fi+∂y∂fj=(∂x∂f,∂y∂f)
说明：函数的方向导数为梯度在该方向上的投影
∇=(∂∂x,∂∂y)\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y})∇=(∂x∂,∂y∂), 引用记号，称为奈布拉(Nebla)算符，或称为向量微分算子或哈密顿(W.R.Hamilton)算子
则梯度可记为：gradf=(∂f∂x,∂f∂y)∇fgrad \ f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) \nabla fgrad f=(∂x∂f,∂y∂f)∇f
- 函数f沿梯度grad f方向，增加最快(上升)
- 函数f沿负梯度 -grad f方向，减小最快(下降)
gradf(x0,y0)=fx′(x0,y0)i+fy′(x0,y0)j)grad \ f(x_0, y_0) = f_x'(x_0, y_0)i + f_y'(x_0, y_0)j)grad f(x0,y0)=fx′(x0,y0)i+fy′(x0,y0)j)
- 或 ∇f(x0,y0)=fx′(x0,y0)i+fy′(x0,y0)j=fx′(x0,y0),fy′(x0,y0)\nabla f(x_0, y_0) = f_x'(x_0, y_0)i + f_y'(x_0, y_0) j = {f_x'(x_0, y_0), f_y'(x_0, y_0)}∇f(x0,y0)=fx′(x0,y0)i+fy′(x0,y0)j=fx′(x0,y0),fy′(x0,y0)
gradf=(∂f∂x,∂f∂y,∂f∂z)=∂f∂xi⃗+∂f∂yj⃗+∂f∂zk⃗grad \ f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}) = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z}\vec{k}grad f=(∂x∂f,∂y∂f,∂z∂f)=∂x∂fi+∂y∂fj+∂z∂fk
- 或 ∇f(x0,y0,z0)={fx′(x0,y0,z0),fy′(x0,y0,z0),fz′(x0,y0,z0)}=fx′(x0,y0,z0)i+fy′(x0,y0,z0)j+fz′(x0,y0,z0)k\nabla f(x_0, y_0, z_0) = \{f_x'(x_0, y_0, z_0), f_y'(x_0, y_0, z_0), f_z'(x_0, y_0, z_0)\} = f_x'(x_0, y_0, z_0)i + f_y'(x_0, y_0, z_0)j + f_z'(x_0, y_0, z_0)k∇f(x0,y0,z0)={fx′(x0,y0,z0),fy′(x0,y0,z0),fz′(x0,y0,z0)}=fx′(x0,y0,z0)i+fy′(x0,y0,z0)j+fz′(x0,y0,z0)k

说明

以三元函数为例，设u=f(x,y,z)u=f(x,y,z)u=f(x,y,z)在点P(x,y,z)处可微分，则函数在该点的梯度为 gradf=∇f=∂f∂xi⃗+∂f∂yj⃗+∂f∂zk⃗=(∂f∂x,∂f∂y,∂f∂z)=(∂(f)∂(x,y,z))grad \ f = \nabla f = \frac{\partial f}{\partial x} \vec{i} + \frac{\partial f}{\partial y} \vec{j} + \frac{\partial f}{\partial z}\vec{k} = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}) = (\frac{\partial (f)}{\partial(x,y,z)})grad f=∇f=∂x∂fi+∂y∂fj+∂z∂fk=(∂x∂f,∂y∂f,∂z∂f)=(∂(x,y,z)∂(f))
梯度是函数u=f(x,y,z)u=f(x,y,z)u=f(x,y,z)在点P处取得的最大方向导数的方向，最大方向导数为：∣gradf∣=(∂f∂x)2+(∂f∂y)2+(∂f∂z)2|grad \ f| = \sqrt{(\frac{\partial f}{\partial x})^2 + (\frac{\partial f}{\partial y})^2 + (\frac{\partial f}{\partial z})^2}∣grad f∣=(∂x∂f)2+(∂y∂f)2+(∂z∂f)2
函数u=f(x,y,z)u=f(x,y,z)u=f(x,y,z)在点P处沿方向l⃗\vec{l}l的方向导数：∂f∂l⃗=gradf⋅l°⃗=∇f⋅l°⃗\frac{\partial f}{\partial \vec{l}} = grad \ f·\vec{l°} = \nabla f · \vec{l °}∂l∂f=grad f⋅l°=∇f⋅l°

例1

求grad1x2+y2grad \ \frac{1}{\sqrt{x^2 + y^2}}grad x2+y21
解：
- 这里f(x,y)=1x2+y2f(x,y) = \frac{1}{x^2 + y^2}f(x,y)=x2+y21
- 因 ∂f∂x=−2x(x2+y2)2,∂f∂y=−2y(x2+y2)2\frac{\partial f}{\partial x} = - \frac{2x}{(x^2 + y^2)^2}, \frac{\partial f}{\partial y} = - \frac{2y}{(x^2 + y^2)^2}∂x∂f=−(x2+y2)22x,∂y∂f=−(x2+y2)22y
- 所以，grad1x2+y2=−2x(x2+y2)2i⃗−2y(x2+y2)2j⃗grad \ \frac{1}{\sqrt{x^2 + y^2}} = - \frac{2x}{(x^2 + y^2)^2} \vec{i} - \frac{2y}{(x^2 + y^2)^2} \vec{j}grad x2+y21=−(x2+y2)22xi−(x2+y2)22yj

例2

设f(x,y,z)=x3−xy2−zf(x,y,z) = x^3 - xy^2 - zf(x,y,z)=x3−xy2−z, p(1,1,0)p(1,1,0)p(1,1,0).
问f(x,y,z)在p处沿什么方向变化最快，在这方向的变化率是多少?
解
- ∇f=fx′i+fy′j+fz′k=(3x2−y2)i−2xyj−k\nabla f = f_x'i + f_y'j + f_z'k = (3x^2 - y^2)i - 2xyj - k∇f=fx′i+fy′j+fz′k=(3x2−y2)i−2xyj−k
- ∇f(1,1,0)=2i−2j−k\nabla f(1,1,0) = 2i - 2j - k∇f(1,1,0)=2i−2j−k
- 沿 ∇f(1,1,0)\nabla f(1,1,0)∇f(1,1,0) 方向，增加最快(上升)
- 沿 −∇f(1,1,0)- \nabla f(1,1,0)−∇f(1,1,0) 方向，增加最快(下降)
- max{∂f∂l∣p}=∣gradf∣=∣∇f(1,1,0)∣=3max\{\frac{\partial f}{\partial l} |_p\} = |grad \ f| = |\nabla f(1,1,0)| = 3max{∂l∂f∣p}=∣grad f∣=∣∇f(1,1,0)∣=3
- min{∂f∂l∣p}=−∣gradf∣=−∣∇f(1,1,0)∣=−3min\{\frac{\partial f}{\partial l} |_p\} = -|grad \ f| = -|\nabla f(1,1,0)| = -3min{∂l∂f∣p}=−∣grad f∣=−∣∇f(1,1,0)∣=−3

AI笔记: 数学基础之方向导数的计算和梯度相关推荐

AI笔记: 数学基础之矩阵的初等变换计算矩阵的秩
引例求解矩阵方程AX=B, 其中 A = ( 2 1 − 3 1 2 − 2 − 1 3 2 ) , B = ( 1 − 1 2 0 − 2 5 ) A =\left (\begin{array}{ ...
AI笔记: 数学基础之偏导数与方向导数
多元函数偏导数在一个多变量的函数中,偏导数就是关于其中一个变量的导数而保持其他变量恒定不变. 假定二元函数z=f(x,y)z=f(x,y)z=f(x,y), 点(x_0, y_0)是其定义域内的一个 ...
AI笔记: 数学基础之联合概率、条件概率与全概率公式
联合概率表示两个事件共同发生的概率,事件A和事件B的共同概率记为:P(AB).P(A,B)P(AB).P(A,B)P(AB).P(A,B) 或者P(A∩B)P(A \cap B)P(A∩B), 记为 ...
AI笔记: 数学基础之概率与统计
概率 1 )概率与频率概率是一个稳定的数值,也就是某件事发生或不发生的概率是多少. 频率是在一定数量的某件事情上面,发生的数与总数的比值. 假设事件A的概率是0.3,在100次中发生28次,那么它的 ...
AI笔记: 数学基础之矩阵运算与行列式
方阵行列式 1 ) 简单的方阵行列式行列式是数学的一个函数,可以看做是几何空间中,一个线性变换对"面积"或"体积"的影响方阵行列式,n阶方阵A的行列式表示为 ...
AI笔记: 数学基础之数字特征-标准差、协方差、相关系数、中心矩、原点矩、峰度、偏度
标准差标准差(Standard Deviation)是离均值平方的算术平均数的平方根,用符号 σ \sigma σ 表示,其实标准差就是方差的算术平方根标准差和方差都是测量离散趋势的最重要.最常见 ...
AI笔记: 数学基础之函数的导数应用及求导公式
关于导数导数是数学中非常重要的概念,它能反应出速度变化的快慢,尤其在AI的算法分析,优化以及数据挖掘中用到很多导数的引出引例1 变速直线运动的速度 s是距离,t是时间,v是速度设描述指点运动的 ...
AI笔记: 数学基础之数字特征-期望与方差
关于 3 σ 3\sigma 3σ法则备注:图片托管于github,请确保网络的可访问性 3 σ 3\sigma 3σ法则: 3 σ 3\sigma 3σ之外的数据可认为异常数据期望期望(mea ...
AI笔记: 数学基础之二项分布与二项式定理
概率试验 1.投掷一个骰子投掷5次 2.某人射击1次,击中目标的概率是0.8, 他射击10次: 3.一个盒子中装有5个球(3红2白),有放回依次从中抽取5个球 4.生产一种零件,出现次品的概率是0.0 ...
AI笔记: 数学基础之向量组的线性表示与线性相关
向量组向量组:有限个相同维度的行向量或列向量组合成的一个集合就叫做向量组A 如果是行向量,那么表示为:A=(a1⃗a2⃗a3⃗⋮an⃗⋮)A = \left (\begin{array}{cccc} ...

AI笔记: 数学基础之方向导数的计算和梯度

方向导数

方向导数

梯度

AI笔记: 数学基础之方向导数的计算和梯度相关推荐

最新文章

热门文章