AI笔记: 数学基础之数字特征-期望与方差

关于 3 σ 3\sigma 3σ法则

备注：图片托管于github，请确保网络的可访问性

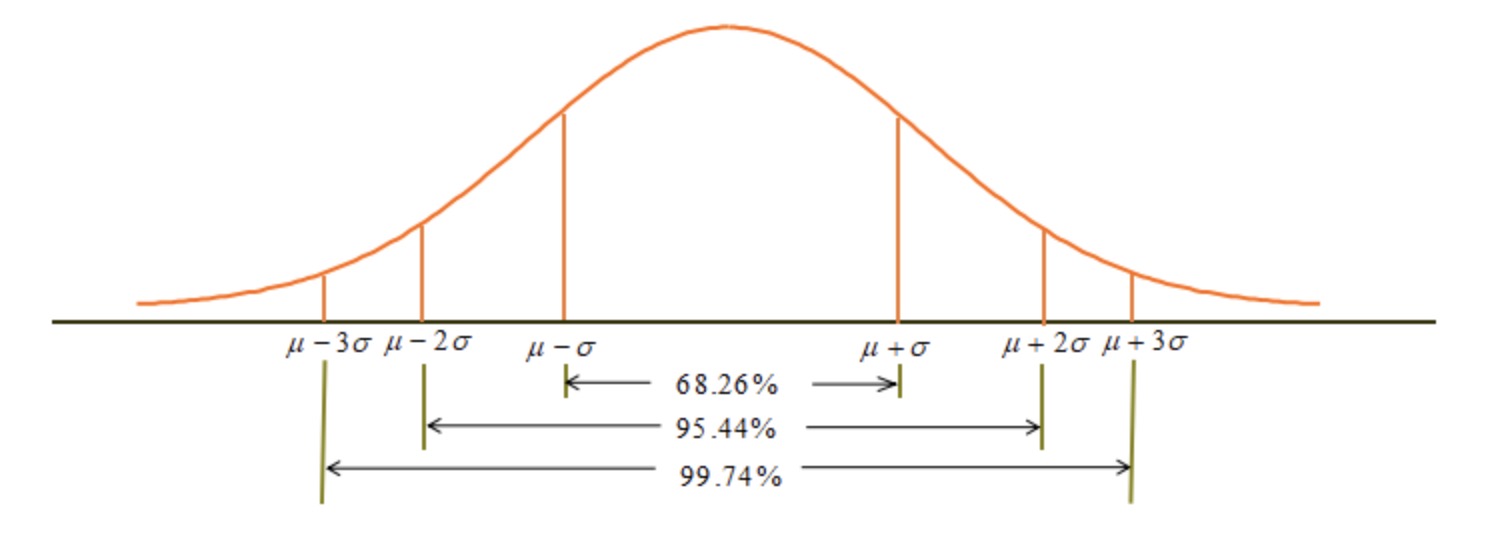
3 σ 3\sigma 3σ法则： 3 σ 3\sigma 3σ之外的数据可认为异常数据

期望

期望(mean): 也就是均值, 是概率加权下的"平均值"，是每次可能结果的概率乘以其结果的总和, 反映的是随机变量平均取值大小, 常用符号 μ \mu μ表示
连续型： E ( X ) = ∫ − ∞ ∞ x f ( x ) d x E(X) = \int_{-\infty}^{\infty} xf(x) dx E(X)=∫−∞∞xf(x)dx
离散型： E ( X ) = ∑ i x i p i E(X) = \sum_i x_i p_i E(X)=∑ixipi

计算期望

每次数据为X,相关发生概率为P(x)，数据如下：
- X: 2， 4， 6， 8， 10
- P(x): 0.2, 0.2, 0.2, 0.2, 0.2
- 则 E ( X ) = ∑ i x i p i = 2 ∗ 0.2 + 4 ∗ 0.2 + 6 ∗ 0.2 + 8 ∗ 0.2 + 10 ∗ 0.2 = 6 E(X) = \sum_i x_i p_i = 2*0.2 + 4*0.2 + 6*0.2 + 8*0.2 + 10*0.2 = 6 E(X)=∑ixipi=2∗0.2+4∗0.2+6∗0.2+8∗0.2+10∗0.2=6

期望性质

假设C为一个常数，X和Y是两个随机变量，那么期望有如下性质
- E© = C
- E(CX) = CE(X)
- E(X+Y) = E(X) + E(Y)
- 如果X和Y相互独立，那么E(XY) = E(X)E(Y)
- 如果E(XY) = E(X)E(Y), 那么X和Y不相关

例1

甲乙两人赌博，假设两人获胜的概率相等，比赛规则是先胜三局者为赢家，可以获得100元的奖励。当比赛进行三局的时候，其中甲剩了2局，乙生了一句，这时候由于一些原因终止了比赛，请问如何分配这100元才比较公平?
分析
- P ( 甲 ) = P ( 乙 ) = 1 2 P(甲) = P(乙) = \frac{1}{2} P(甲)=P(乙)=21
- P ( 甲赢 ) = P ( 赢 4 ) + P ( 赢 5 ，输 4 ) = 1 2 + 1 2 ∗ ( 1 − 1 2 ) = 3 4 P(甲赢) = P(赢4) + P(赢5，输4) = \frac{1}{2} + \frac{1}{2} * (1-\frac{1}{2}) = \frac{3}{4} P(甲赢)=P(赢4)+P(赢5，输4)=21+21∗(1−21)=43
- P ( 乙赢 ) = P ( 赢 5 , 赢 4 ) = 1 2 ∗ 1 2 = 1 4 P(乙赢) = P(赢5, 赢4) = \frac{1}{2} * \frac{1}{2} = \frac{1}{4} P(乙赢)=P(赢5,赢4)=21∗21=41
- E ( 甲 ) = 100 ∗ P ( 甲赢 ) = 100 ∗ 3 4 = 75 E(甲) = 100 * P(甲赢) = 100 * \frac{3}{4} = 75 E(甲)=100∗P(甲赢)=100∗43=75
- E ( 乙 ) = 100 ∗ P ( 乙赢 ) = 100 ∗ 1 4 = 25 E(乙) = 100 * P(乙赢) = 100 * \frac{1}{4} = 25 E(乙)=100∗P(乙赢)=100∗41=25

例2

某城市有10万个家庭，没有孩子的家庭有1000个, 有一个孩子的有9万个，有两个孩子的家庭有6000个, 有三个孩子的家庭有3000个, 问次城市一个家庭平均有小孩多少个?
分析
- X: 0, 1, 2, 3
- P: 0.01, 0.9, 0.06, 0.03
- E ( X ) = ∑ i = 0 3 x i p ( x i ) = 0 ∗ 0.01 + 1 ∗ 0.9 + 2 ∗ 0.06 + 3 ∗ 0.03 = 1.11 E(X) = \sum_{i=0}^3 x_i p(x_i) = 0 * 0.01 + 1 * 0.9 + 2 * 0.06 + 3 * 0.03 = 1.11 E(X)=∑i=03xip(xi)=0∗0.01+1∗0.9+2∗0.06+3∗0.03=1.11

例3

甲乙两人射击，他们的射击水平由下表给出
X:甲击中的环数，Y：乙击中的环数
甲：
- X: 8, 9, 10
- P: 0.1, 0.3, 0.6
乙：
- X: 8, 9, 10
- P: 0.2, 0.5, 0.3
试问哪个人射击的水平较高?
分析
- 甲乙的平均环数为：
  - E X = 8 ∗ 0.1 + 9 ∗ 0.3 + 10 ∗ 0.6 = 9.5 EX = 8*0.1 + 9*0.3 + 10*0.6 = 9.5 EX=8∗0.1+9∗0.3+10∗0.6=9.5
  - E Y = 8 ∗ 0.2 + 9 ∗ 0.5 + 10 ∗ 0.3 = 9.1 EY = 8*0.2 + 9*0.5 + 10*0.3 = 9.1 EY=8∗0.2+9∗0.5+10∗0.3=9.1
- 所以，从平均环数上看，甲的射击水平要比乙的好

方差

方差(variance)是衡量随机变量或一组数据时离散程度的度量，是用来度量随机变量和其数学期望之间的偏离程度。即方差是衡量数据源数据和期望均值相差的度量值。
V a r ( X ) = D ( X ) = σ 2 = ∑ ( X − μ ) 2 N Var(X) = D(X) = \sigma^2 = \frac{\sum (X - \mu)^2}{N} Var(X)=D(X)=σ2=N∑(X−μ)2
D ( X ) = ∑ i = 1 n p i ⋅ ( x i − u ) 2 D(X) = \sum_{i=1}^n p_i · (x_i - u)^2 D(X)=∑i=1npi⋅(xi−u)2
D ( X ) = ∫ a b ( x − μ ) 2 f ( x ) d x D(X) = \int_a^b (x - \mu)^2 f(x) dx D(X)=∫ab(x−μ)2f(x)dx
D ( X ) = E ( ( X − E ( x ) ) 2 ) = E ( X 2 ) − ( E ( X ) ) 2 D(X) = E((X-E(x))^2) = E(X^2) - (E(X))^2 D(X)=E((X−E(x))2)=E(X2)−(E(X))2

计算一组数据的方差

X: 2， 4， 6， 8， 10
P(x): 0.2, 0.2, 0.2, 0.2
分析
- E ( X ) = 6 E(X) = 6 E(X)=6
- E ( X 2 ) = 44 E(X^2) = 44 E(X2)=44
- D ( X ) = E ( X 2 ) − ( E ( X ) ) 2 = 44 − 6 2 = 8 D(X) = E(X^2) - (E(X))^2 = 44 - 6^2 = 8 D(X)=E(X2)−(E(X))2=44−62=8

例1

甲乙两人射击，他们的射击水平由下表给出：
X: 甲击中的环数，Y: 乙击中的环数
甲
- X: 8, 9, 10
- P: 0.3, 0.2, 0.5
乙
- X: 8, 9, 10
- P: 0.2, 0.4, 0.4
试问哪个人的射击水平较高?
分析
- 比较两个人的平均环数
- 甲的平均环数：EX = 80.3 + 90.2 + 10*0.5 = 9.2
- 乙的平均环数：EY = 80.2 + 90.4 + 10*0.4 = 9.2
- 因此，从平均环数来看，甲乙两人的射击水平是一样的，但两人射击环数的方差分别为：
  - D X = ( 8 − 9.2 ) 2 ∗ 0.3 + ( 9 − 9.2 ) 2 ∗ 0.2 + ( 10 − 9.2 ) 2 ∗ 0.5 = 0.76 DX = (8-9.2)^2 * 0.3 + (9-9.2)^2 * 0.2 + (10-9.2)^2 * 0.5 = 0.76 DX=(8−9.2)2∗0.3+(9−9.2)2∗0.2+(10−9.2)2∗0.5=0.76
  - D Y = ( 8 − 9.2 ) 2 ∗ 0.2 + ( 9 − 9.2 ) 2 ∗ 0.4 + ( 10 − 9.2 ) 2 ∗ 0.4 = 0.624 DY = (8-9.2)^2 * 0.2 + (9-9.2)^2 * 0.4 + (10-9.2)^2 * 0.4 = 0.624 DY=(8−9.2)2∗0.2+(9−9.2)2∗0.4+(10−9.2)2∗0.4=0.624
- 由于DY < DX，表明乙的射击水平比甲稳定

方差性质

假设C为一个常数，X和Y两个随机变量，那么方差有以下性质
- D ( C ) = 0 D(C) = 0 D(C)=0
- D ( C X ) = C 2 D ( X ) D(CX) = C^2D(X) D(CX)=C2D(X)
- D ( C + X ) = D ( X ) D(C+X) = D(X) D(C+X)=D(X)
- D ( X ± Y ) = D ( X ) + D ( Y ) ± 2 C o v ( X , Y ) D(X \pm Y) = D(X) + D(Y) \pm 2Cov(X,Y) D(X±Y)=D(X)+D(Y)±2Cov(X,Y)
- 协方差 C o v ( X , Y ) = E { ( X − E ( X ) ) ⋅ ( Y − E ( Y ) ) } Cov(X,Y) = E\{ (X - E(X)) · (Y - E(Y)) \} Cov(X,Y)=E{(X−E(X))⋅(Y−E(Y))}
- 如果X和Y不相关, 那么KaTeX parse error: Undefined control sequence: \pmY at position 4: D(X\̲p̲m̲Y̲) = D(X) + D(Y)

常见分布

备注：图片托管于github，请确保网络的可访问性

AI笔记: 数学基础之数字特征-期望与方差相关推荐

AI笔记: 数学基础之数字特征-标准差、协方差、相关系数、中心矩、原点矩、峰度、偏度
标准差标准差(Standard Deviation)是离均值平方的算术平均数的平方根,用符号 σ \sigma σ 表示,其实标准差就是方差的算术平方根标准差和方差都是测量离散趋势的最重要.最常见 ...
概率 | 【提神醒脑】自用笔记串联二 —— 数字特征、大数定律、统计量
本文总结参考于 kira 2023概率提神醒脑技巧班. 笔记均为自用整理.加油!ヾ(◍°∇°◍)ﾉﾞ第一部分笔记详见概率 | [提神醒脑]自用笔记串联一 -- 事件.随机变量及其分布_西皮呦的博客 ...
机器学习的数学基础（一）—— 期望、方差、协方差与相关系数
0. 期望与方差期望: E[aX+bY]=aE[X]+bE[Y] E[aX+bY]=aE[X]+bE[Y] 方差: D(aX+bY)=D(aX)+D(bY)+2cov(aX,bY)=a2D(X)+b ...
AI笔记: 数学基础之联合概率、条件概率与全概率公式
联合概率表示两个事件共同发生的概率,事件A和事件B的共同概率记为:P(AB).P(A,B)P(AB).P(A,B)P(AB).P(A,B) 或者P(A∩B)P(A \cap B)P(A∩B), 记为 ...
AI笔记: 数学基础之向量组的线性表示与线性相关
向量组向量组:有限个相同维度的行向量或列向量组合成的一个集合就叫做向量组A 如果是行向量,那么表示为:A=(a1⃗a2⃗a3⃗⋮an⃗⋮)A = \left (\begin{array}{cccc} ...
AI笔记: 数学基础之概率与统计
概率 1 )概率与频率概率是一个稳定的数值,也就是某件事发生或不发生的概率是多少. 频率是在一定数量的某件事情上面,发生的数与总数的比值. 假设事件A的概率是0.3,在100次中发生28次,那么它的 ...
AI笔记: 数学基础之函数的导数应用及求导公式
关于导数导数是数学中非常重要的概念,它能反应出速度变化的快慢,尤其在AI的算法分析,优化以及数据挖掘中用到很多导数的引出引例1 变速直线运动的速度 s是距离,t是时间,v是速度设描述指点运动的 ...
AI笔记: 数学基础之二项分布与二项式定理
概率试验 1.投掷一个骰子投掷5次 2.某人射击1次,击中目标的概率是0.8, 他射击10次: 3.一个盒子中装有5个球(3红2白),有放回依次从中抽取5个球 4.生产一种零件,出现次品的概率是0.0 ...
AI笔记: 数学基础之正交矩阵与矩阵的QR分解
正交矩阵若n阶方阵A满足ATA=EA^TA = EATA=E, 则称A为正交矩阵, 简称正交阵 (复数域上称为酉矩阵) A是正交阵的充要条件:A的列(行)向量都是单位向量,且两两正交. 若A为正交矩 ...

AI笔记: 数学基础之数字特征-期望与方差

关于 3 σ 3\sigma 3σ法则

期望

方差

AI笔记: 数学基础之数字特征-期望与方差相关推荐

最新文章

热门文章