博弈论入门——威佐夫博弈

规则： 有两堆石子，两人轮流操作，每次可以从某一堆中取走一些石子，也可以同时从两堆石子中取走相同数量的石子，数量不限，但不能不取。无法操作的人失败。

我们可以通过枚举发现 (0, 0)、(1, 2)、(2, 1)、(3, 5)、(5, 3) 这些状态都属于必败态。但同样的，如果想接着往后枚举推理又变得困难了起来。好在这个游戏只有两堆石子，我们可以将两堆石子数 x, y 映射到平面直角坐标系的点 (x, y) 上，使得游戏的每一个局面都对应坐标中的一个点，这样就可以用平面图来辅助我们进行分析。游戏的两种操作则表示坐标点向左、向下或向左下移动任意距离。

于是我们就可以画出这样的一张图

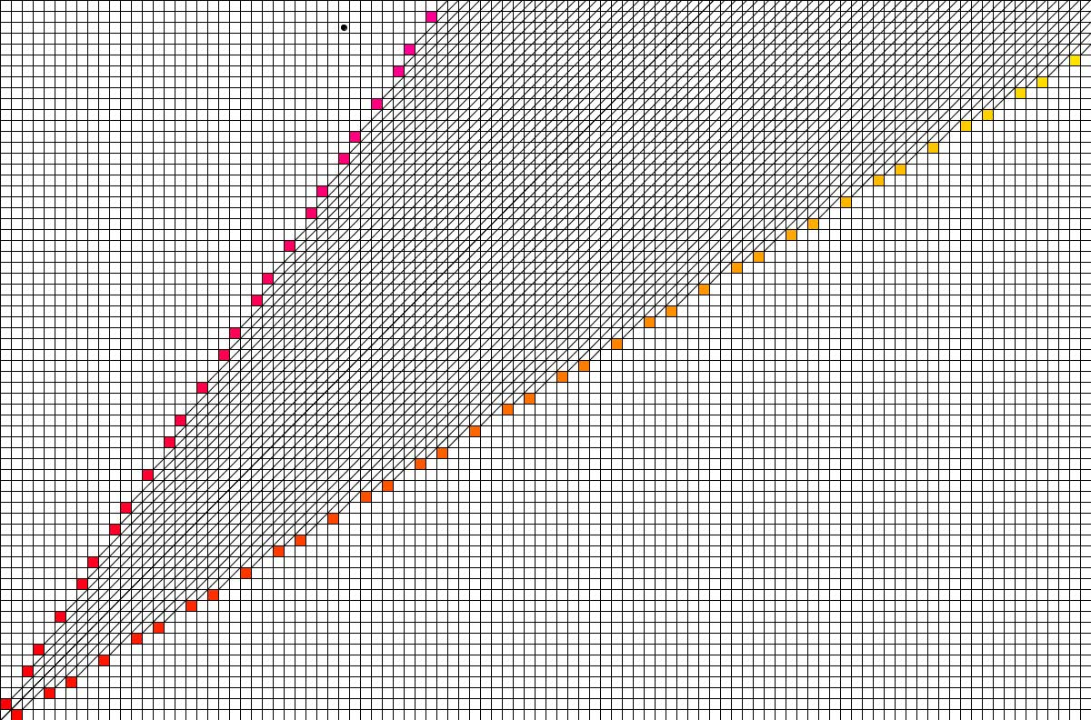
先解释下这张图是如何画出来的，首先 (0, 0) 点一定是必败态，我们把 (0, 0) 点标记为红色。然后将 (0, 0) 点右方、上方以及右上方的所有点都标为绿色。这些点都是必胜态，因为这些点对应的状态都可以直接转移至必败态 (0, 0)。然后我们要找到下一个必败态，才好递推地找出所有必败态和必胜态。回忆一下必败态的性质，必败态只能转移至必胜态。于是不难发现点 (1, 2) 的左侧、下侧以及左下侧的所有点的状态都以已确定了，都为必胜态，即点 (1, 2) 所有可转移的状态都为必胜态，所以该点为必败态。同理，点 (2, 1) 也为必败态。我们将这两点标红，再将它们右侧、上侧以及右上侧的所有点标绿。如此往复，我们就可以递推地找出所有的必胜态和必败态了。

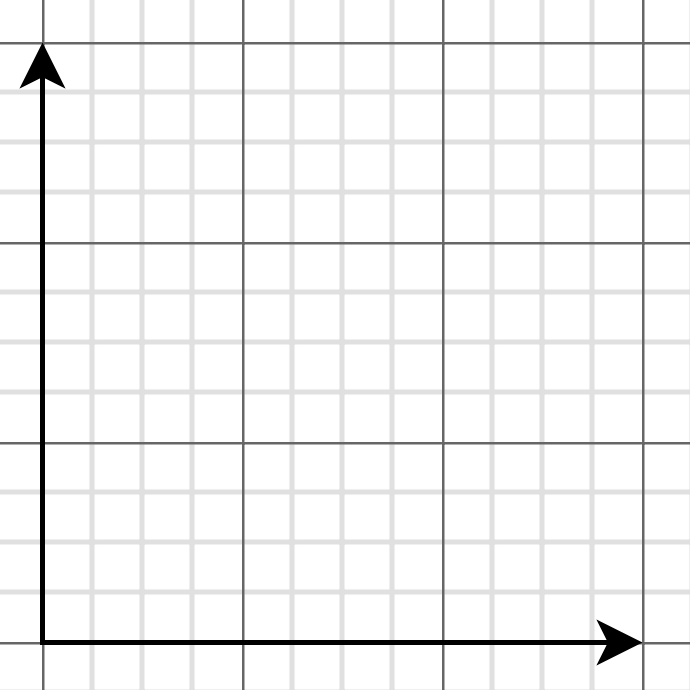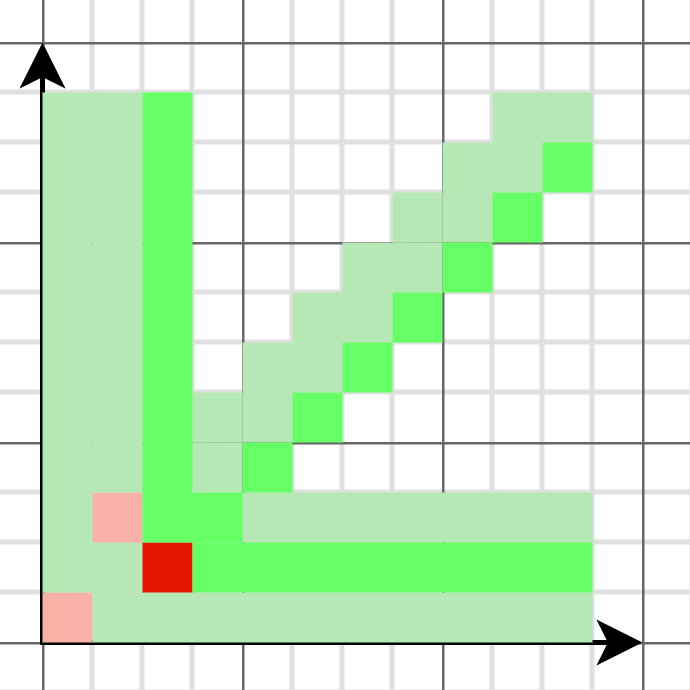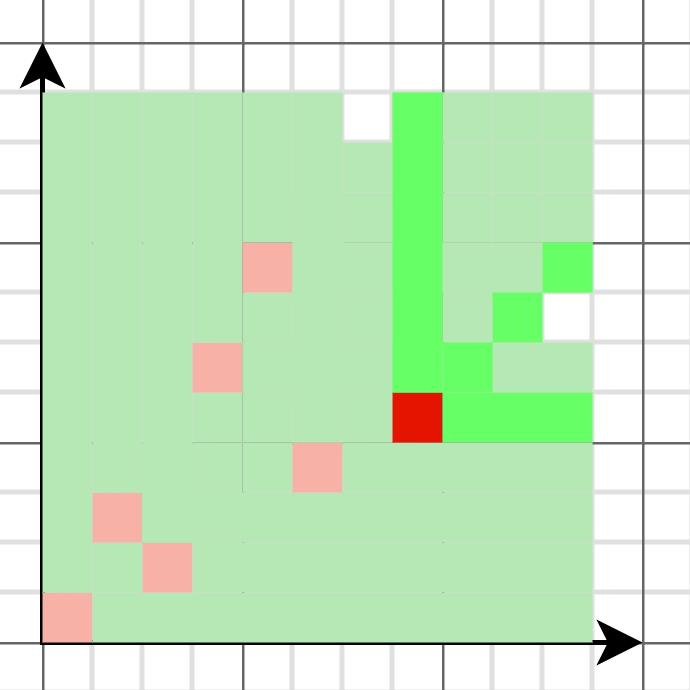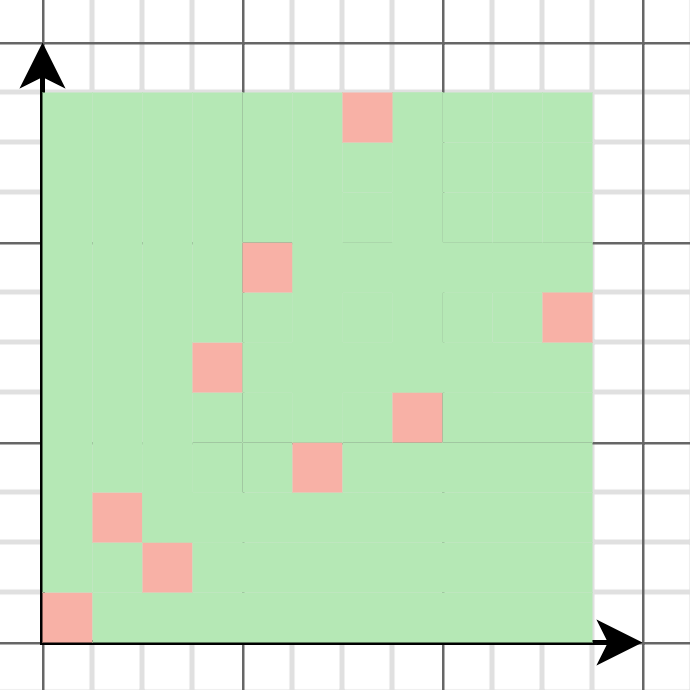
从图中可以看出，这些必败点似乎是线性的，如果描的点足够多，就会发现这些点连成的线的斜率接近黄金比例 1.618，这不是巧合，实际上这些必败点的组成的集合满足

即

直接推出这个结论较为困难，所以这里还是先给出结论再加以证明

证明这个结论是否正确，只需证 W 不重不漏地包括了所有必败点。

点集 W 具有以下性质：

W 中各点的 x 值组成的整数集不重不漏地包含每一个正整数，y 值同理
W 中各点的 x 与 y 的差值不重不漏地包含所有整数，且当 x < y 时，y - x 随着 x 增大而递增，当 x > y 时，x - y 随着 x 增大而递增

性质 1 证明：

这里需要引入 Beatty 定理，若存在两个无理数 a, b，满足

则对于以下两个集合

有

简单证明一下 Beatty 定理，我们先考虑区间 [1, n]，在 A 和 B 在区间中的元素个数分别为

我们知道对于两个正数 a, b，有

于是

又由于

所以

又因为 a, b 为无理数，所以

所以

即

于是集合 A 与集合 B 的元素个数之和正好等于区间 [1, n] 中的正整数个数。又由于在区间 [1, n+1] 上时，A 和 B 的元素个数之和为 n 个，即随着区间右端点地移动，元素个数也随之增加，说明 A 和 B 正好不重复地包含了区间 [1, n] 上的所有整数。

根据 Beatty 定理，由于

所以

由于对称性，某一点的 x 值会与另一点的 y 值相同。

性质 2 证明：

由于黄金比例满足

式子左右同乘 i 于是有

即

由于减号两端均为无理数，相减得到整数说明小数点后的数相等，取整不影响结果

所以

以下通过这两条性质证明 W 不重不漏地包括了所有必败点：

设 (x1, y1), (x2, y2) 为 W 中的两个点：

若 (x1 - k, y1) = (x2, y2) 则有 y1 = y2 与 W 的性质 1 矛盾。同理，不存在 (x1, y1 - k) = (x2, y2 - k)。故无法通过只改变 x 或 y 使得 W 中的一个点变为另一个点。
若 (x1 - k, y1 - k) = (x2, y2) ，则有 y1 - x1 = y2 - x2 与 W 的性质 2 矛盾。故也无法通过同时改变 x 和 y 使得 W 中的一个点变为另一个点。

综上，点集 W 中的任意一个点无法一步变为 W 中的另一个点。

设 (a, b) 为 W 的补集中的一个点 (a < b)：

在点集 W 中寻找一个点 (x0, y0)，使得 a = x0，根据性质 1 可知该点一定存在

若 b > y0 ，则存在 k 使得 (a, b - k) = (x0, y0)，即点 (a, b) 可以一步变为 W 中的点
若 b < y0 ，说明 y0 - x0 > b - a，由 W 的性质 2 可知 W 中存在点 (x1, y1) 满足 y1 - x1 = b - a 且 x1 < x0 = a。故存在 k 使得 (a - k, b - k) = (x1, y1)，即点 (a, b) 可以一步变为 W 中的点

以上仅考虑了 a < b 的情况，由于对称性，当 a > b 时也同理。而当 a = b 时，(a, b) 可直接转移至点 (0, 0)

综上，W 的补集中的任意一个点都可以一步变为 W 中。

所以 W 满足必败态的两个条件，因此原命题得证。

博弈论入门——威佐夫博弈相关推荐

【博弈论】威佐夫博弈
简介威佐夫博弈( W y t h o f f G a m e Wythoff\ Game Wythoff Game):有两堆物品个数是 n n n和 m m m,甲乙两个人轮流从一堆选取 k k k ...
博弈论入门之威佐夫博弈
威佐夫博弈威佐夫博弈是一类经典的博弈问题有两堆石子,两个顶尖聪明的人在玩游戏,每次每个人可以从任意一堆石子中取任意多的石子或者从两堆石子中取同样多的石子,不能取得人输,分析谁会获得胜利博弈分析 ...
【小组专题二：博弈论入门综述（1）】NP状态 | SG函数 | 巴什博奕、威佐夫博弈、斐波那契博弈、Nim游戏、SJ定理
博弈论综述[1] 前言博弈与博弈论博弈树 NP状态 SG函数(Sprague-Grundy) Sprague-Grundy Theorem 巴什博奕 Bash Game 威佐夫博弈扩展威佐夫博弈 ...
博弈论（巴什博奕，威佐夫博弈，尼姆博弈）
巴什博奕(Bash Game): 只有一堆n个物品,两个人轮流从中取物,规定每次最少取一个,最多取m个,最后取光者为胜举一个最简单的例子就是,当n=m+1时,此时不管先手取多少,后手都能把剩下的取完 ...
博弈论（巴什博弈，威佐夫博弈，尼姆博弈）
文章目录一.巴什博弈二.威佐夫博弈三.尼姆博弈一.巴什博弈一堆n个物品,两个人从中轮流取出1~m个,最后取关者胜. 同余定理:n=K*(m+1)+r;先取者拿走r个,那么后者无论拿走(1~m ...
博弈论（巴什博奕，威佐夫博弈，尼姆博弈，斐波那契博弈）
一. 巴什博奕(Bash Game): A和B一块报数,每人每次报最少1个,最多报4个,看谁先报到30.这应该是最古老的关于巴什博奕的游戏了吧. 其实如果知道原理,这游戏一点运气成分都没有,只和先手 ...
博弈论（巴什博弈）（威佐夫博弈）（尼姆博奕）
1.巴什博弈:只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个.最后取光者得胜. 解释:这个理解简单,n%(m+1)==0时,先手定会输.比如n=3,m=2:你先取,你取1 ...
BZOJ3298[USACO 2011Open]cow checkers——威佐夫博弈
题目描述一天,Besssie准备和FJ挑战奶牛跳棋游戏.这个游戏上在一个M*N的棋盘上, 这个棋盘上在(x,y)(0<=x棋盘的左下角是(0,0)坐标,棋盘的右上角是坐标(M-1,N-1). ...
Nim博弈和威佐夫博弈 Return of the Nim
Nim博弈 Nim游戏的概述: 还记得这个游戏吗? 给出n列珍珠,两人轮流取珍珠,每次在某一列中取至少1颗珍珠,但不能在两列中取.最后拿光珍珠的人输. 后来,在一份资料上看到,这种游戏称为" ...
威佐夫博弈算法C++
在看本文章之前给大家说几句如果你是先看了百度上的解释或者是其他文章,觉得很是繁琐,无法理解. 那么恭喜你,看本文会轻松很多.这里没有讲解原理之类的,只是结果.当你理解了之后,有兴趣的话就可以继续去钻 ...

博弈论入门——威佐夫博弈

博弈论入门——威佐夫博弈相关推荐

最新文章

热门文章