方向导数、梯度、等高线、数量场与向量场

转载自：http://blog.csdn.net/lijil168/article/details/69367531

之前用过几次梯度下降算法来求解一些优化问题，但对梯度的具体意义并不是很理解。前一段时间翻了一遍高教的《简明微积分》，对梯度概念总算有了些理解，在这记录一下。

推荐下《简明微积分》这本书，我向来对带有“简明”二字的书抱有极大的好感。偶然的机会在豆瓣上看到有人推荐这本书，作者是龚升先生。龚升先生是中国科技大学教授，师从华罗庚。我个人觉得这本书是我读过的最好的国内的数学教材，结构条理，不拖沓但重点突出，适合快速的回顾微积分课程。

为什么会有方向导数？

在微积分课程中，我们知道函数在某一点的导数（微商）代表了函数在该点的变化率。微分和积分，它们的定义都是建立在极限的基础上。对于单变量函数f(x)，它在x0处导数是：当x趋近于x0时，函数的改变量与自变量的改变量的比值的极限，即微商（导数）等于差商的极限

f′(x0)=limΔx→0f(x0+Δx)−f(x0)Δx

对于单变量函数，自变量只有一个，当x趋近于x0时只能在直线上变动，移动的方向只有左右两方。

然而，对于多变量函数，自变量有多个，表示自变量的点在一个区域内变动，不仅可以移动距离，而且可以按任意的方向来移动同一段距离。因此，函数的变化不仅与移动的距离有关，而且与移动的方向有关。因此，函数的变化率是与方向有关的。这也才有了方向导数的定义，即某一点在某一趋近方向上的导数值。假设给定函数u=u(M)，取一点M0=(x0,y0,z0)，L是由M0出发的任一直线，则u在M0点L的方向导数定义为

(∂u∂L)M0=limM→M0M∈Lu(M)−u(M0)|MM0|

梯度

上面有了方向导数的定义，我们进一步来推导方向导数的表示，命L的方向余弦为(cosα,cosβ,cosγ)，则L上的M可表示为

x=x0+tcosα,y=y0+tcosβ,z=z0+tcosγt=|MM0|

。于是u对L的方向导数为

(∂u∂l)M0=limt→0Δut=limt→0∂u∂xΔx+∂u∂yΔy+∂u∂zΔz+o(t)t=limt→0t(∂u∂xcosα+∂u∂ycosβ+∂u∂zcosγ)+o(t)t=∂u∂xcosα+∂u∂ycosβ+∂u∂zcosγ

注意，在上面的推导中用到了全微分公式。

令向量，L方向可以表示为。因为l是一个单位向量，所以

(∂u∂L)M0=n∗l=|n|cosθ

这表达了L上的方向导数其实是梯度矢量n与单位矢量L的点积。 当L与n同向时， (∂u∂L)M0 便取得最大值|n|，我们称n为u在该点的梯度。可以看到梯度即是某一点最大的方向导数，沿梯度方向函数有最大的变化率（正向增加，逆向减少）。

另外还可以证明，在某一点的梯度方向，就是过该点的等值面的切平面的法线方向。但需要注意的是，这并不是定理，只是等值函数的法向量的表达式与函数的梯度的表达式一致而已，并非两者之间必然的存在关系。因此，在某一点沿着梯度看去，等值面分布最密，即达到临近等值面的距离最小。

我们知道，一般说来二元函数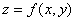在几何上表示一个曲面，这曲面被平面z=c(c是常数)所截得的曲线_{（等高线）}的方程为

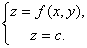
这条曲线在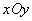面上的投影是一条平面曲线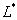（图8―10），它在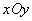平面直角坐标系中的方程为

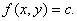
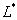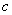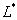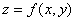对于曲线上的一切点，已给函数的函数值都是，所以我们称平面曲线为函数的等高线.

由于等高线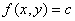上任一点处的法线的斜率为

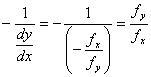所以梯度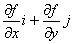

为等高线上点处的法向量，因此我们可得到梯度与等高线的下述关系：函数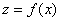在点的梯度的方向与过点的等高线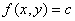在这点的法线的一个方向相同，且从数值较低的等高线指向数值较高的等高线，而梯度的模等于函数在这个法线方向的方向导数.这个法线方向就是方向导数取得最大值的方向.

多变量函数的极值

对于单变量函数，若在某点取得极值，则该点的导数为0。同样对于多变量函数，在某点为极大值或极小值只有当在该点的每个偏导数等于0才有可能，也就是说梯度等于0。因此，在多变量函数中，驻点，也就是导数为0的点，指的是每个偏导数等于0，也就是梯度等于0的点。进而，在求极值时，我们可以先找到梯度为0的驻点，在通过定理（查书呗）判断它是否是极值点，极大值还是极小值。

.数量场与向量场

如果对于空间区域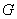内的任一点，都有一个确定的数量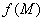，则称在这空间区域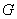内确定了一个数量场（例如温度场、密度场）等.一个数量场可用一个数量函数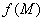来确定.如果与点相对应的是一个向量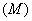，则称在这空间区域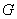内确定了一个向量场（例如力场，速度场等）.一个向量场可用一个向量函数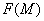来确定，而

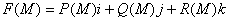其中是点的数量函数.

利用场的概念，我们可以说向量函数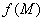确定了一个向量场——梯度场，它是由数量场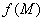产生的.通常称函数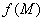为这个向量场的势.而这个向量场又称为势场.必须注意，任意一个向量场不一定是势场，因为它不一定是某个数量函数的梯度场.

方向导数、梯度、等高线、数量场与向量场相关推荐

三度其一——数量场的梯度
数量场的梯度方向导数,分别沿着 l1,l2l_1,l_2l1,l2 方向的变化率沿着这一段的平均变化率 u(P)−u(M)MP→u(P)-u(M) \over {\overrightarrow ...
高数学习日记——矢量场与数量场的概念
用于个人理解概念与记录,一定很不专业. 矢量场与数量场数量场类似于一般见到的 U(x)=f(x,y,z) 这样的函数,就可以描述一个数量场,因为每一个确定的 (x,y,z)坐标,都会有一个确定的函 ...
高等数学：第八章多元函数微分法及其应用（3）方向导数梯度多元函数的极值
§8.7 方向导数与梯度一.方向导数 1.定义设函数在点的某一邻域内有定义,自点引射线,设轴正向到射线的转角为,为邻域内且在上的另一点. 若比值这里,当沿着趋向于时的极限存在,称此极限值为函数 ...
[Machine Learning] 方向导数梯度（Directional Derivative Gradient）
方向导数首先,我们先来讨论一下函数 y = f ( x 1 , x 2 ) y = f(x_1,x_2) y=f(x1,x2)在一点P沿某一方向的变化率问题. 假设函数 y = f ( x 1 ...
数量场的等值面与矢量场的矢量线的一些基本的东西（写得不好）
一个数量场里,等值面有无穷多个. 一个空间可以看作有无穷多个等值面穿套而成. 一个空间里面,任意两个等值面不能相交,如果两个等值面相交,相交处取何值? 工程规定,c2−c1=c3−c2c_2-c_1= ...
全微分/偏导数/方向导数/梯度/全导数
1.偏导数参考 :导数.偏导数.方向导数就是对某一变量求导,把其他变量作为常数 2.方向导数可以认为偏导数是特殊的方向导数,是在自变量方向上的方向导数. 任意方向导数为: 3.梯度参考: 导数 ...
第七节方向导数与梯度
教学目的:掌握方向导数的定义和求法:掌握梯度的定义.求法及其与等高线的关系. 教学重点:方向导数与梯度的求法. 教学难点:方向角的确定. 教学内容: 一.方向导数现在我们来讨论函数在一点沿某一方向的 ...
导数，偏导，方向倒数，梯度
导数: 导数不仅仅表示该点切线的斜率,还反应了函数在该点的变化率. 偏导数: 偏导数仅仅是表示某点在x方向的导数和再y轴方向的导数. 这反应了偏导数的局限性,仅仅是多元函数沿着坐标轴的变化率,但是如上 ...
什么是损失函数？什么是梯度
什么是损失函数? 损失函数就一个具体的样本而言,模型预测的值与真实值之间的差距. 对于一个样本(xi,yi)其中yi为真实值,而f(xi)为我们的预测值.使用损失函数L(f(xi),yi)来表示真实值 ...

方向导数、梯度、等高线、数量场与向量场

方向导数、梯度、等高线、数量场与向量场相关推荐

最新文章

热门文章