导数,偏导,方向倒数,梯度
导数:
导数不仅仅表示该点切线的斜率,还反应了函数在该点的变化率。

偏导数:

偏导数仅仅是表示某点在x方向的导数和再y轴方向的导数。
这反应了偏导数的局限性,仅仅是多元函数沿着坐标轴的变化率,但是如上图,在M0点处存在很多方向的偏导数(并不仅仅x和y方向)。这就引出了方向导数。
方向导数:
我们不仅仅要知道函数在坐标轴方向上的变化率(即偏导数)还需要设法求得函数在其他方向上的变化率。而方向导数就是函数在其他特定方向上的变化率。
方向导数的定义和导数定义类似,只不过是在多个维度上。例如在三维空间中:
设三元函数f在点P0(x0,y0,z0)的某邻域内有定义,l为从点P0出发的射线,P(x,y,z)为l上且含于邻域内的任一点,以ρ(rou)表示P和P0两点间的距离。若极限lim( (f(P)-f(P0)) / ρ )= lim (△l f / ρ)(当ρ→0时)存在,则称此极限为函数f在点P0沿方向l的方向导数
梯度:
由上面的方向导数可知,方向导数是在各个方向上都有,而且每个方向上的变化一般是不一样的,那到底沿哪个方向最大呢?沿哪个方向最小呢?为了研究方便,就有了梯度的定义。
下图是梯度的定义:

梯度是众多方向导数中最大(方向指向数值增长最快的方向,大小为变化率)的那个向量,这个方向就用梯度来表示(grad=ai+bj)这个向量来表示,其中a是函数在x方向上的偏导数,b是函数在y方向上的偏导数,梯度的模就是这个最大方向导数的值。
参考:http://www.matongxue.com/madocs/222.html#/madoc
梯度与导数的关系 (一元导数k,梯度k*i )
梯度可谓是多元函数中一个基本的名词。它的物理意义:方向指向数值增长最快的方向,大小为变化率(学习率)。通过这个性质也说明梯度是有方向和大小的矢量。通过梯度的定义我们发现,梯度的求解其实就是求函数偏导的问题,而我们高中所学的导数在非严格意义上来说也就是一元的“偏导”。通过这一点我们自然而然地想到梯度应该是导数向更高维数的推广。然而一我一直想不明白的是: 梯度是矢量而某点的导数是个常量,两者应该有本质的区别,而导数的正负也反映了函数值的大小变化,而不是一直指向数值增大的方向。
在此我们通过一张图来说明解释一下两者的关系:
其实一元函数肯定也有梯度,我们经常不提及的原因其实很简单:一元函数的梯度方向自变量轴(x)!而导数值的正负号决定了这个方向是正方向还是反方向。如图所示,A点右"领域"的导数为正值,则梯度的方向跟x轴正方向一致,梯度方向指向数值增大的方向;相反在B点右"领域",导数为负值,则梯度的方向为x轴的负方向,梯度方向也是指向数值增大的方向。通过这个例子向多维函数推广,梯度从数值小指向数值大的物理意义也就容易理解了。而一元函数的大小自然也就是导数的绝对值。
方向导数与梯度实例
一、方向导数
现在我们来讨论函数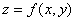 在一点
在一点 沿某一方向的变化率问题.
沿某一方向的变化率问题.
定义 设函数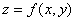 在点
在点
 的某一邻域
的某一邻域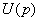 内有定义.自点
内有定义.自点 引射线
引射线 .设
.设 轴正向到射线
轴正向到射线 的转角为
的转角为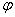 (逆时针方向:
(逆时针方向: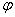
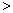 0;顺时针方向:
0;顺时针方向: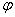
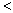 0),并设
0),并设 '(
'( +△
+△ ,
,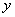 +△
+△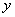 )为
)为 上的另一点且
上的另一点且 '∈
'∈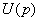 .我们考虑函数的增量
.我们考虑函数的增量 (
( +△
+△ ,
,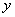 +△
+△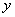 )-
)-
 与
与 、
、 '两点间的距离
'两点间的距离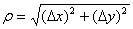 的比值.当
的比值.当 '沿着
'沿着 趋于
趋于 时,如果这个比的极限存在,则称这极限为函数
时,如果这个比的极限存在,则称这极限为函数
 在点
在点 沿方向
沿方向 的方向导数,记作
的方向导数,记作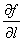 ,即
,即
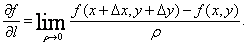 (1)
(1)
从定义可知,当函数
 在点
在点
 的偏导数
的偏导数 x、
x、 y存在时,函数在点
y存在时,函数在点 沿着
沿着 轴正向
轴正向
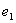 =
=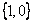 ,
,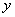 轴正向
轴正向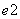 =
=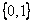 的方向导数存在且其值依次为
的方向导数存在且其值依次为 x、
x、 y,函数
y,函数
 在点
在点 沿
沿 轴负向
轴负向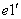 =
=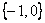 ,
,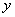 轴负向
轴负向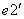 =
=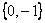 的方向导数也存在且其值依次为-
的方向导数也存在且其值依次为- x、-
x、- y.
y.
关于方向导数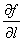 的存在及计算,我们有下面的定理.
的存在及计算,我们有下面的定理.
定理 如果函数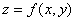 在点
在点
 是可微分的,那末函数在该点沿任一方向的方向导数都存在,且有
是可微分的,那末函数在该点沿任一方向的方向导数都存在,且有
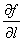
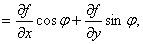 (2)
(2)
其中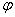 为
为 轴到方向
轴到方向 的转角.[360度] cos(r)=@l/@x
的转角.[360度] cos(r)=@l/@x
证 根据函数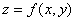 在点
在点
 可微分的假定,函数的增量可以表达为
可微分的假定,函数的增量可以表达为
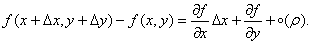
(直接相加不好吧),向量,a--b;ax-by;ay;bx; x,y正交 独立
两边各除以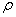 ,得到
,得到
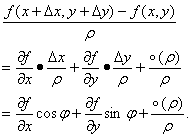
所以 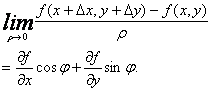
 这就证明了方向导数存在且其值为
这就证明了方向导数存在且其值为
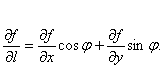
例8-26 求函数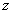 =
=
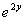 在点
在点
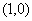 处沿从点
处沿从点
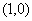 到点
到点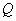
 方向的方向导数.
方向的方向导数.
解 这里方向 即向量
即向量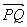 =
=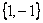 的方向,因此
的方向,因此 轴到方向
轴到方向 的转角
的转角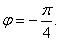 ,
,
因为 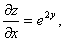

在点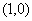 ,
,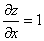 ,
,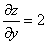 .故所求方向导数
.故所求方向导数
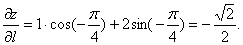
例8-27 设由原点到点 的向径为
的向径为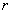 ,
, 轴到
轴到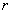 的转角为
的转角为 ,
, 轴到射线
轴到射线 的转角为
的转角为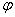 ,求
,求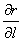 ,其中
,其中 =
=
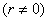 .
.
解 因为 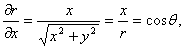
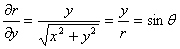 .
.
所以 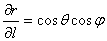

由例8-26可知,当 时,
时,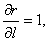 ,即
,即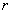 沿着向径本身方向的方向导数为1;而当
沿着向径本身方向的方向导数为1;而当 时,
时, , 即
, 即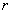 沿着与向径垂直方向的方向导数为零.
沿着与向径垂直方向的方向导数为零.
对于三元函数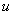 =
=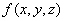 来说,它在空间一点
来说,它在空间一点
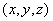 沿着方向
沿着方向 (设方向
(设方向 的方向角为
的方向角为 的方向导数,同样可以定义为
的方向导数,同样可以定义为
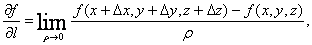 (3)
(3)
其中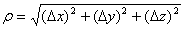 ,△
,△ =
=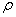
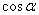 ,△
,△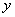 =
=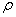
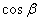 ,△
,△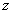 =
=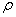
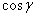 .
.
同样可以证明,如果函数在所考虑的点处可微分,那末函数在该点沿着方向 的方向导数为
的方向导数为

二、 梯度
1.梯度的定义
与方向导数有关联的一个概念是函数的梯度.
定义 设函数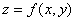 在平面区域
在平面区域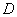 内具有一阶连续偏导数,则对于每一点
内具有一阶连续偏导数,则对于每一点
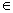
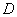 ,都可定出一个向量
,都可定出一个向量
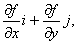
这向量称为函数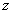 =
= 在点
在点
 的梯度,记作
的梯度,记作

 ,即
,即


 =
= 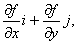
如果设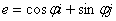 是与方向
是与方向 同方向的单位向量,则由方向导数的计算公式可知
同方向的单位向量,则由方向导数的计算公式可知
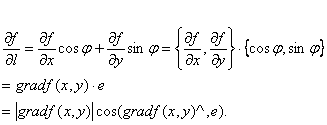
这里,(

 ^,e)表示向量
^,e)表示向量

 与
与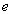 的夹角.由此可以看出,就是梯度在射线
的夹角.由此可以看出,就是梯度在射线 上的投影,当方向
上的投影,当方向 与梯度的方向一致时,有
与梯度的方向一致时,有
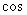 (
(

 ^,
^,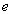 )
) 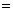 1,
1,
从而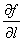 有最大值.所以沿梯度方向的方向导数达到最大值,也就是说,梯度的方向是函数
有最大值.所以沿梯度方向的方向导数达到最大值,也就是说,梯度的方向是函数
 在这点增长最快的方向.因此,我们可以得到如下结论:
在这点增长最快的方向.因此,我们可以得到如下结论:
函数在某点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值.
由梯度的定义可知,梯度的模为
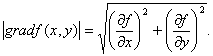
当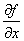 不为零时,那
不为零时,那 轴到梯度的转角的正切为
轴到梯度的转角的正切为
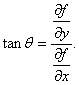
我们知道,一般说来二元函数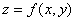 在几何上表示一个曲面,这曲面被平面z=c(c是常数)所截得的曲线
在几何上表示一个曲面,这曲面被平面z=c(c是常数)所截得的曲线 的方程为
的方程为
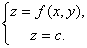
这条曲线 在
在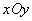 面上的投影是一条平面曲线
面上的投影是一条平面曲线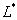 (图8―10),它在
(图8―10),它在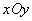 平面直角坐标系中的方程为
平面直角坐标系中的方程为
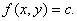
对于曲线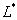 上的一切点,已给函数的函数值都是
上的一切点,已给函数的函数值都是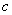 ,所以我们称平面曲线
,所以我们称平面曲线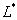 为函数
为函数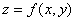 的等高线.
的等高线.
由于等高线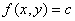 上任一点
上任一点 处的法线的斜率为
处的法线的斜率为
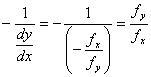 ,
,
所以梯度 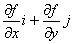
为等高线上点 处的法向量,因此我们可得到梯度与等高线的下述关系:函数
处的法向量,因此我们可得到梯度与等高线的下述关系:函数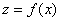 在点
在点
 的梯度的方向与过点
的梯度的方向与过点 的等高线
的等高线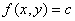 在这点的法线的一个方向相同,且从数值较低的等高线指向数值较高的等高线(图8―10),而梯度的模等于函数在这个法线方向的方向导数.这个法线方向就是方向导数取得最大值的方向.
在这点的法线的一个方向相同,且从数值较低的等高线指向数值较高的等高线(图8―10),而梯度的模等于函数在这个法线方向的方向导数.这个法线方向就是方向导数取得最大值的方向.
例8-28 求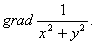
解 这里 
因为 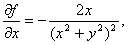

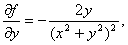
所以 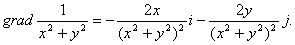
3.数量场与向量场
如果对于空间区域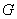 内的任一点
内的任一点 ,都有一个确定的数量
,都有一个确定的数量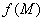 ,则称在这空间区域
,则称在这空间区域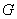 内确定了一个数量场(例如温度场、密度场)等.一个数量场可用一个数量函数
内确定了一个数量场(例如温度场、密度场)等.一个数量场可用一个数量函数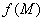 来确定.如果与点
来确定.如果与点 相对应的是一个向量
相对应的是一个向量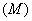 ,则称在这空间区域
,则称在这空间区域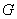 内确定了一个向量场(例如力场,速度场等).一个向量场可用一个向量函数
内确定了一个向量场(例如力场,速度场等).一个向量场可用一个向量函数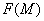 来确定,而
来确定,而
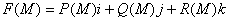 ,
,
其中 是点
是点 的数量函数.
的数量函数.
利用场的概念,我们可以说向量函数
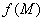 确定了一个向量场——梯度场,它是由数量场
确定了一个向量场——梯度场,它是由数量场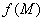 产生的.通常称函数
产生的.通常称函数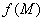 为这个向量场的势.而这个向量场又称为势场.必须注意,任意一个向量场不一定是势场,因为它不一定是某个数量函数的梯度场.
为这个向量场的势.而这个向量场又称为势场.必须注意,任意一个向量场不一定是势场,因为它不一定是某个数量函数的梯度场.
小结:本节主要研究函数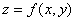 在一点
在一点 沿某一方向的变化率问题,给出方向导数的定义及其相关的梯度的定义,推导出方向导数和梯度的求法,并通过梯度的意义介绍了等高线、等量面、数量场与向量场等概念.
沿某一方向的变化率问题,给出方向导数的定义及其相关的梯度的定义,推导出方向导数和梯度的求法,并通过梯度的意义介绍了等高线、等量面、数量场与向量场等概念.

作业:
1.求函数 在点(1,2)处沿从点(1,2)到点(2,2+
在点(1,2)处沿从点(1,2)到点(2,2+ )的方向的方向导数.
)的方向的方向导数.
2.求函数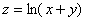 在抛物线
在抛物线 上点(1,2)处,沿着这抛物线在该点处偏向x轴正向的切线方向的方向导数.
上点(1,2)处,沿着这抛物线在该点处偏向x轴正向的切线方向的方向导数.
3.求函数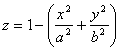 在点
在点 处沿曲线
处沿曲线 在这点的内法线方向的方向导数.
在这点的内法线方向的方向导数.
导数,偏导,方向倒数,梯度相关推荐
- python如何求导数(derivative)、求偏导(partial derivative)?(sympy库symbols()函数、diff()函数、subs()函数)
可以使用Sympy库 SymPy是一个符号计算的Python库.它的目标是成为一个全功能的计算机代数系统,同时保持代码简洁.易于理解和扩展.它完全由Python写成,不依赖于外部库. SymPy支持符 ...
- 导数,微分,偏导,全微分,方向导数,梯度
多元函数与一元函数有一个很大的区别在于定义域的不同:一元函数自变量就在x轴上,因此趋近的方向只有某点的左右两侧,因此,考察一元函数极限的时候,仅考虑左邻域和右邻域即可.但是多变量微分变得复杂,趋向方式 ...
- 二元隐函数求二阶偏导_在线计算专题(03):具体、抽象函数的导数、微分与方向导数的计算...
导数与微分是微积分内容的基础,就计算来说一元函数与多元函数的导数的计算思想一致. 不管是一元函数还是多元函数,导数.偏导数的计算都是将函数视为求导变量的一元函数求导数.微分在描述形式略有区别,但是其计 ...
- 偏导,梯度,Hesse矩阵的一些概念和求函数的极值
偏导 偏导函数..简称为偏导数 可以理解为,固定一个变量,求另一个变量的导数; 三元函数的二阶偏导有9个 梯度 梯度(由偏导数组成的一个向量) 梯度的特点: 1 方向,函数变化率最大的方向;(负梯度方 ...
- 极限和连续+偏导+方向导数+可微+梯度+链式法则+hessian矩阵
文章目录 前言 一.极限和连续 二.偏导数 三.方向导数 四.可微 五.梯度 六.链式法则 七.Hessian矩阵 前言 多元函数 y对某一个变量的导数是偏导数: 偏导数的结果可以推广到任意方向,也就 ...
- 偏导,方向导数以及梯度的理解
最初的疑惑 在梯度的Wiki 上对梯度在三维空间,直角坐标系下的梯度表示为 ∇ = ∂ f ( x , y , z ) ∂ x ∗ i ⃗ + ∂ f ( x , y , z ) ∂ y ∗ j ⃗ ...
- 梯度下降算法_梯度下降算法中的偏导公式推导
前言:最近在跟着吴恩达老师(Andrew Ng)的视频课程学习机器学习,该视频是2014年拍的,虽然有点老,但理论却并不过时,是非常经典的机器学习入门教程,也正是因为这是入门教程,所以视频中的有些数学 ...
- 手动求梯度,二范数的偏导,二范数平方的偏导
单位向量对自身的导数: 在向量方向变化时,导数不为0 在向量方向不变时 (实数空间),导数为0 https://math.stackexchange.com/questions/2983445/uni ...
- Jacobian矩阵 梯度矩阵 矩阵偏导与微分 例子与常见公式
Jacobian矩阵 梯度矩阵 矩阵偏导与微分 常见公式 矩阵求导是机器学习中常见的运算方法,研究对象包括标量矩阵,求导分为标量矩阵求导,矩阵求导. 根据个人理解和经验,机器学习中的优化目标一般是一个 ...
最新文章
- 【青少年编程竞赛交流】03月份微信图文索引
- 用STL给C++充电:第一部分
- 经典排序算法(4)——折半插入排序算法详解
- 数论六之计算几何干货——计算几何模板解释全集 及 模板检验训练场
- 使用Arquillian测试安全的EJB
- MySql 错误 Err [Imp] 1153 - Got a packet bigger than 'max_allowed_packet' bytes
- LaTex插入PDF图片并调整它的宽度
- sqlite 数据量_Sqlite数据库从入门到放弃
- 使用Xamarin在Visual Studio中开发Android应用
- AI学习笔记(十三)CNN之人脸检测
- 我的博客搬家工具开发
- C4D 展UV的那些坑
- 蓝桥杯第四届初赛“模拟智能灌溉系统”设计任务书
- 2022世界杯看球指南
- 法国蓬皮杜中心天猫官方旗舰店开业;洲际集团旗下高端品牌voco全球开业及签约酒店数突破100家 | 美通企业日报...
- java excel 判断组重复_Java判断Excel某列是否有重复值
- matlab如何表示冲激信号,matlab里如何表示冲激信号
- 为什么浏览器会限制ajax并行请求数量,有办法突破限制吗
- 引力产生的原因是什么
- Mac如何安装numpy,pandas,matplotlib,spicy等包,以及下载速度慢遇到read timed out问题如何解决
