在概率论中所说的事件(event)相当于集合论中的集合(set)。

互补事件的概率

　　如果一个不出现，则另一个肯定出现的两个事件成为互补事件(complementary events，或者互余事件或对立事件).按照集合的记号，如果一个事件记为A，那么另一个记为的补集。P(A) + P(A) = 1 ,P(A) = 1 − P(A)。(初中学的吧）

比如西方赌博时常常爱用优势或赔率。如果你赢的概率为0.6，那么就说成是你有6对4的优势会赢，或者4对6的优势会输。

概率的加法

　　如果两个事件不可能同时发生，那么至少其中之一发生的概率为这两个事件的概率和。比如"抛一次骰子得到5或者5点"的概率是"得到5点"的概率与"得到6点"的概率之和，即1/6 + 1/6 = 1/3。但是如果两个事件可能同时发生时这样做就不对了。

　　假设抛骰子时，一个事件A为"得到偶数点"(有可能是2,4,6点)，另一个事件B为"得到大于或等于3点"(有4种可能:3,4,5,6点)，这样事件A的概率显然等于3/6 = 1/2,即P（A) = 1/2,而事件B的概率为P（B）=2/3.但是,"得到大于或等于3点或者偶数点"的事件的概率就不是P(A) + P(B) = 1/2 + 2/3 = 7/6了，概率怎么能够大于1呢？其实这多出来的就是A与B的共同部分的概率。

概率的乘法

　　如果有一个固定电话和一个手机，假定固定电话出毛病的概率为0.01，而手机出问题的概率为0.05，那么两个同时出毛病的概率是多少呢？ 上过初中的都能立马算出是0.01乘以0.05,但这种法则，仅仅在两个事件独立(independent)时才成立。如果事件不独立则需要引进条件概率(conditional probability)。

　　比如三个人抽签，而只有一个人能够抽中，因此每个人抽中的机会是1/3。假定用A1、A2、A3分别代表着三种人抽中的事件，那么，P(A1)=P(A2)=P(A3)=1/3，但是由于一个人抽中，其他人不可能抽中，所以，这三个事件不独立。所以一般地在一个事件B已经发生的情况下，事件A发生的条件概率定位就为：

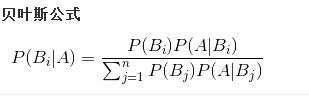
变量的分布

　　随机变量取一切可能值或范围的概率或概率的规律成为概率分布(probability distribution,简称分布).一个概率分布是和某总体(population)也称为样本空间(sampling space)相联系的。

　　在确定了抽样方法后，这个有限总体就可能与概率有关的总体有某种联系了，并且可能对诸如总体比例等进行推断。这里的总体或样本空间为一个抽象的空间，它是由某种试验的所有可能结果点组成的，这些结果的获得都服从某种概率规律。因此，一个总体(样本空间)是由一个取值范围及相连的概率所组成的。

离散随机变量的分布

　　离散随机变量只取离散的值，比如骰子的点数、次品的个数、得病的人数等等。每一种取值都有某种概率，各种取值点的概率总和应该是1.当然离散变量不仅限于取非负整数值。一般来说，某离散随机变量的每一个可能取值x都相当于取该值的概率P(xi).

二项分布

　　比如，每个进入某商场的顾客都有购买或不购买商品的两种可能、每个被调查的人士会支持或不支持某种观点、每一个产妇有生出或不生出男婴或女婴两种可能等等。根据这种简单试验的分布，可以得到基于这个试验的更加复杂事件的概率。

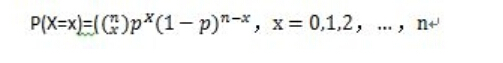
这里

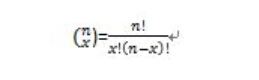
为二项式系数。 这里P(x)为n次试验中成功k次的概率，p为每次试验成功的概率。不过现在很多统计学工具要统计二项分布的都已经直接实现了~

多项分布为二项分布的推广，就好比调查顾客对5个品牌的饮料的选择中，每种品牌都会以一定的概率中选，假定这些概率为p1,p2,p3,p4,p5。每次试验的结果只可能有一个，因此这些概率的和为1，即p1+p2+p3+p4+p5 = 1，在二项分布中，人们关心的是在n次实验中成功k次的概率(有了成功k次的概率，就有了失败n-k次的概率)。但是在多项分布问题中，所关心的就是在n次试验中，选择5个品牌的人数分别为m1,m2,m3,m4,m5的概率，自然，m1+m2+m3+m4+m5=n。

超几何分布

　　超几何分布和有限总体的不放回抽样的实践有密切关系。比如有一批500个产品，而其中有5个次品，质量检查人员随即抽取20个产品进行检查。如果抽到的20个产品中含有2个或更多不合格产品，则整个500个产品都将会退会。那么该批产品退回的概率是多少呢？ 这里就满足了超几何分布。 这是一种不放回的抽样，如果放回的话那么这个物品还可能会被抽上，那么每次抽样时得到次品的概率是一样的，等于次品的比例，这就不是超几何分布而是二项分布了。这里的产品总数为n，其中不合格产品数为k，不放回抽样的数目为N，而样本中有M个不合格的产品的概率就为: