平面上任意椭圆与点的位置关系

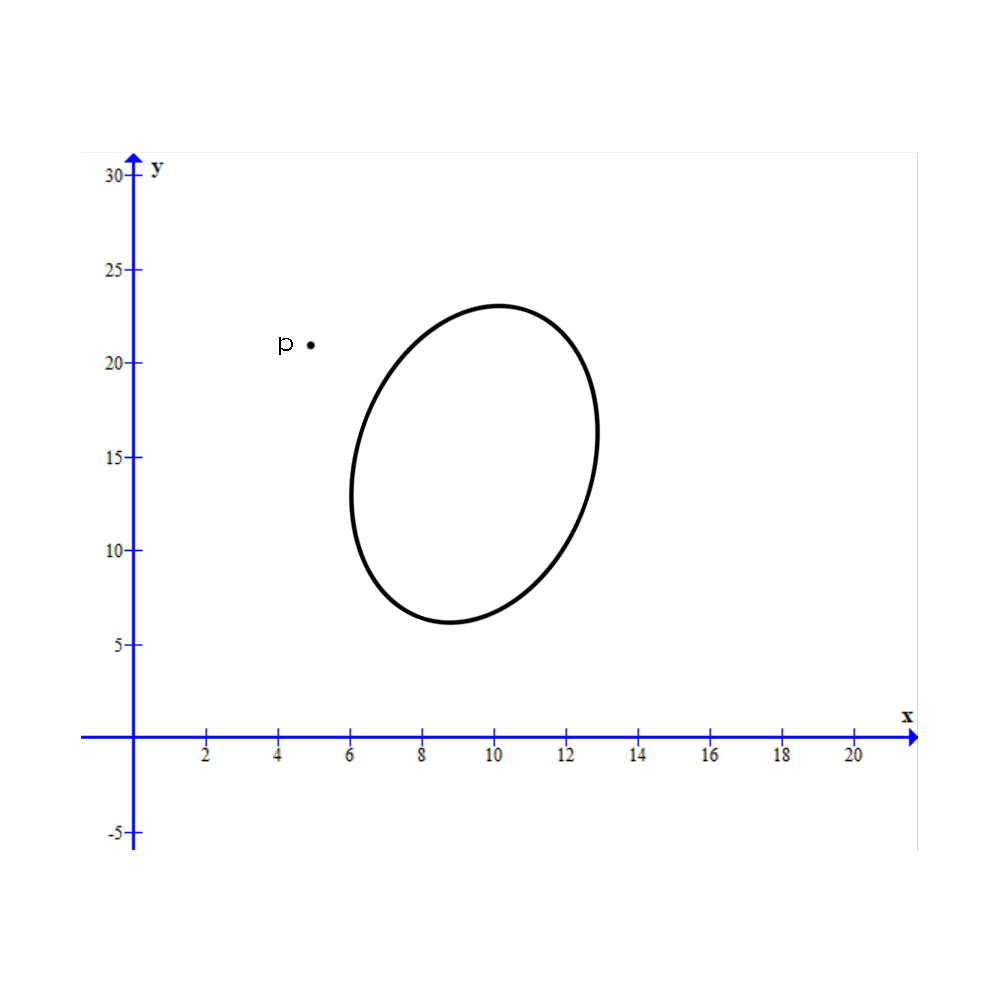
问题描述 : 如上图所示，我们的目的是判断在二维空间中任意一椭圆与任意一点pi(xi,yi)p_i(x_i,y_i)pi(xi,yi)的位置关系，这样的位置关系有三种 : 1 点在椭圆上; 2 点在椭圆中; 3 点在椭圆外。

解决思路 :

从最简单的开始讲起, 在初中时候学到过，对于一个焦点在xxx轴或yyy轴的椭圆来讲有标准方程 :
x2a2+y2b2=1\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1
或者
y2a2+x2b2=1\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1 a2y2+b2x2=1
利用标准方程，判断点与椭圆的位置关系十分容易，以焦点在xxx轴上的椭圆为例,∀p(xi,yi)∈R2\forall p(x_i,y_i)\in R^2∀p(xi,yi)∈R2，这里不加证明的给出位置关系的判别式 :
(1) 若
xi2a2+yi2b2<1\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} < 1 a2xi2+b2yi2<1
点在椭圆内；
(2) 若
xi2a2+yi2b2=1\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} = 1 a2xi2+b2yi2=1
点在椭圆上；
(3) 若
xi2a2+yi2b2>1\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} > 1 a2xi2+b2yi2>1
点在椭圆外。
这一块证明的资料很多，在此就不再赘述了。

现在将问题泛化 : 对于任意的一个椭圆如何求其与点pip_ipi的关系。根据上面的结论我们可以很自然的思考，如果通过一种坐标系的变换，将任意的椭圆都变为焦点在xxx轴，或yyy轴的椭圆，那么其与点pip_ipi位置关系的判断将是十分容易，只需要带入已知公式即可，根据这样的思路，我们建立如下坐标系。

如上图所示，在新的坐标系x′0′y′x'0'y'x′0′y′中，椭圆的焦点处于坐标轴上，可以使用椭圆的标准方程进行求解，唯一的问题是如何将任给一点pip_ipi变换到x′0′y′x'0'y'x′0′y′，证明的方式有很多种，在此选用基变换.
下述方法中,变换后向量的起点0′0'0′的坐标是(x0,y0)(x_0,y_0)(x0,y0)点，为了满足这个条件，首先对pip_ipi进行简单的平移变换，
xi=xi−x0yi=yi−y0x_i = x_i - x_0 \\ y_i = y_i - y_0 xi=xi−x0yi=yi−y0
注 :(x0,y0)(x_0,y_0)(x0,y0) 是椭圆圆心坐标.

求解 :
在原始坐标系x0yx0yx0y中选取一组单位正交基{e1⃗,e2⃗},e1⃗=(1,0),e2⃗=(0,1)\{ \vec{e_1},\vec{e_2} \},\vec{e_1} = (1,0),\vec{e_2} = (0,1){e1,e2},e1=(1,0),e2=(0,1)，显然pi⃗=xie1⃗+yie2⃗\vec{p_i} = x_i \vec{e_1} + y_i \vec{e_2}pi=xie1+yie2.
如上图先将e1⃗,e2⃗\vec{e_1},\vec{e_2}e1,e2旋转θ\thetaθ角，根据向量旋转公式:
(e1′⃗)T=[cos⁡(θ)−sin⁡(θ)sin⁡(θ)cos⁡(θ)]⋅[10](e2′⃗)T=[cos⁡(θ)−sin⁡(θ)sin⁡(θ)cos⁡(θ)]⋅[01](\vec{e_1'})^T = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ (\vec{e_2'})^T = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix} (e1′)T=[cos(θ)sin(θ)−sin(θ)cos(θ)]⋅[10](e2′)T=[cos(θ)sin(θ)−sin(θ)cos(θ)]⋅[01]
综上e1′⃗=(cos⁡θ,sin⁡θ),e2′⃗=(−sinθ,cosθ)\vec{e_1'} = \left ( \cos \theta ,\sin\theta \right ),\vec{e_2'} = (-sin\theta,cos\theta)e1′=(cosθ,sinθ),e2′=(−sinθ,cosθ), 显然其满足这几点 :
(1) e1′⃗,e2′⃗\vec{e_1'},\vec{e_2'}e1′,e2′ 线性无关
(2) e1′⃗⋅e2′⃗=0\vec{e_1'}\cdot\vec{e_2'} = 0e1′⋅e2′=0
(3) ∣e1′⃗∣=∣e2′⃗∣=1\left | \vec{e_1'} \right | = \left | \vec{e_2'} \right | = 1∣∣∣e1′∣∣∣=∣∣∣e2′∣∣∣=1
以上通过旋转矩阵求出了新坐标系下的一组正交基，下面只需要求pi⃗\vec{p_i}pi在新的基下的表示即可,解法有多种，下面展示一种通过求过度矩阵来进行求解的方法 :
将e1′⃗,e2′⃗\vec{e_1'},\vec{e_2'}e1′,e2′通过e2⃗,e2⃗\vec{e_2},\vec{e_2}e2,e2进行表示 :
e1′⃗=cos⁡θ⋅e1⃗+sin⁡θ⋅e2⃗e2′⃗=−sin⁡θ⋅e1⃗+cos⁡θ⋅e2⃗\vec{e_1'} = \cos\theta \cdot \vec{e_1} + \sin\theta \cdot \vec{e_2} \\ \vec{e_2'} = -\sin\theta \cdot \vec{e_1} + \cos\theta \cdot \vec{e_2} \\ e1′=cosθ⋅e1+sinθ⋅e2e2′=−sinθ⋅e1+cosθ⋅e2
由上可以求出过渡矩阵
C=[cos⁡(θ)−sin⁡(θ)sin⁡(θ)cos⁡(θ)]C = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix}C=[cos(θ)sin(θ)−sin(θ)cos(θ)]
所以e1⃗,e2⃗\vec{e_1},\vec{e_2}e1,e2到e1′⃗,e2′⃗\vec{e_1'},\vec{e_2'}e1′,e2′的坐标变换表示为 :
[xi′yi′]=C−1⋅[xiyi]\begin{bmatrix} x_i'\\ y_i' \end{bmatrix} = C^{-1}\cdot \begin{bmatrix} x_i \\ y_i \end{bmatrix} [xi′yi′]=C−1⋅[xiyi]
整理可以得到 :
x′=cos⁡θ⋅x+sin⁡θ⋅yy′=−sin⁡θ⋅x+cos⁡θ⋅yx' = \cos\theta \cdot x + \sin\theta \cdot y \\ y' = -\sin\theta \cdot x + \cos\theta \cdot y x′=cosθ⋅x+sinθ⋅yy′=−sinθ⋅x+cosθ⋅y
上述关系式还可以通过向量间的投影关系得到.

最后将变换后的(xi′,yi′)(x'_i,y'_i)(xi′,yi′)带入判别式，计算即可。