tags: Combinatorics

写在前面

前面铺垫了很多偏序集和格,分配格等的基本知识, 下面开始以这些代数结构为研究对象, 探寻其上的一些性质与关系, 我们先以关联代数的定义开始说起.

关联代数简介

定义

令Int(P)\mathrm{Int}(P)Int(P)表示PPP上所有的区间的集合, (空集不是区间)
令KKK为一个域, 定义f:Int(P)→Kf:{\rm Int}(P)\to Kf:Int(P)→K, 用f(x,y)f(x,y)f(x,y)表示f([x,y])f([x,y])f([x,y]).

PPP在KKK上的关联代数I(P,K)I(P,K)I(P,K)定义为: 由所有的函数f:Int(P)→Kf:{\rm Int}(P)\to Kf:Int(P)→K构成的KKK-代数, 其中乘法(卷积)定义为:

(fg)(x,y)=∑x≤⁣⋅⁣ z≤yf(x,z)g(z,y).(fg)(x,y)=\sum_{x\leq {\Large{}_{\stackrel{\!\,{}_z}{\,\!{}^\cdot}}}\leq y}f(x,z)g(z, y). (fg)(x,y)=x≤⋅z≤y∑f(x,z)g(z,y).

且关联代数I(P,K)I(P,K)I(P,K)有双侧单位元的结合KKK-代数, 单位元记为δ\deltaδ或者111,定义为

δ(x,y)={1,if x=y,0,if x≠y.\delta(x,y)= \begin{cases} 1, & \text{if}\ x=y,\\ 0, & \text{if}\ x\ne y. \end{cases} δ(x,y)={1,0,if x=y,if x=y.

取数域K=CK=\mathbb CK=C即可, 可将I(P,C)I(P,\mathbb C)I(P,C)简记为I(P)I(P)I(P).

另一种表达:

将I(P,K)I(P,K)I(P,K)视为由所有的形式表达式:

f=∑[x,y]∈Int(P)f(x,y)[x,y]f=\sum_{[x,y]\in \mathrm{Int}(P)}f(x,y)[x,y] f=[x,y]∈Int(P)∑f(x,y)[x,y]

组成的, 其中卷积定义如下:

[x,y]⋅[z,w]={[x,w],if y=z,0,if y≠z,[x,y]\cdot[z,w]=\begin{cases} [x,w],&\text{if }y=z,\\[5pt] 0,&\text{if } y\ne z, \end{cases} [x,y]⋅[z,w]=⎩⎨⎧[x,w],0,if y=z,if y=z,

并且通过双线性(允许[x,y][x,y][x,y]的无限线性组合)扩展到所有的I(P,K)I(P,K)I(P,K).

有限情形的例子

如果PPP有限, 其中元素记为x1,⋯,xnx_1,\cdots,x_nx1,⋯,xn, 其中xi<xj⇒i<jx_i<x_j\Rightarrow i<jxi<xj⇒i<j, 于是I(P)I(P)I(P)同构于C\mathbb CC上满足: 若xi≰xjx_i\not\leq x_jxi≤xj则mij=0m_{ij}=0mij=0的上三角矩阵M=(mij),1≤i,j≤nM=(m_{ij}),\ 1\le i,j\le nM=(mij), 1≤i,j≤n构成的代数. (可以从mijm_{ij}mij到f(xi,xj)f(x_i,x_j)f(xi,xj)建立映射关系)

如果PPP由下图给出, 则I(P)I(P)I(P)同构于形式为

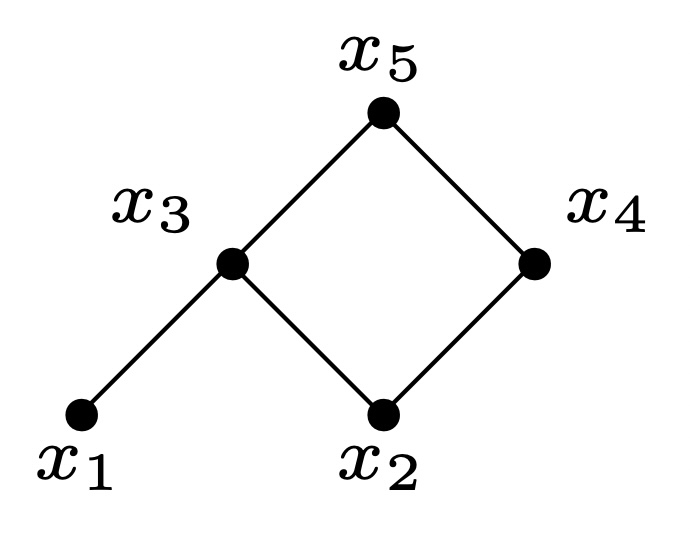$$ \begin{bmatrix} ∗ & 0 & ∗ & 0 & ∗\\ 0 & ∗ & ∗ & ∗ & ∗\\ 0 & 0 & ∗ & 0 & ∗\\ 0 & 0 & 0 & ∗ & ∗\\ 0 & 0 & 0 & 0 & ∗\\ \end{bmatrix} $$ 的矩阵构成的代数.

性质

设f∈I(P)f\in I(P)f∈I(P), 则下面的条件等价:

fff有一个左逆元;
fff有一个右逆元;
fff有一个双侧逆元(必然是唯一的左逆元和右逆元);
f(x,x)≠0,∀x∈Pf(x,x)\ne0,\ \forall x\in Pf(x,x)=0, ∀x∈P成立.

进一步, 如果f−1f^{-1}f−1存在, 则f−1(x,y)f^{-1}(x,y)f−1(x,y)仅取决于偏序集[x,y][x,y][x,y].

证明:

设fg=δfg=\deltafg=δ, 等价于∀x∈P\forall x\in P∀x∈P, 有f(x,x)g(x,x)=1f(x,x)g(x,x)=1f(x,x)g(x,x)=1, ∀x,y∈P\forall x,y\in P∀x,y∈P, 且满足x<yx<yx<y, 有

KaTeX parse error: Limit controls must follow a math operator at position 35: …-1}{\large\sum}\̲l̲i̲m̲i̲t̲s̲_{x<z\le y}f(x,…

于是fff有右逆元g⟺∀x∈P,f(x,x)≠0g\iff \forall x\in P, f(x,x)\ne0g⟺∀x∈P,f(x,x)=0, 并且此时f−1(x,y)f^{-1}(x,y)f−1(x,y)仅取决于[x,y][x,y][x,y].

同理, 设hf=δhf=\deltahf=δ, 即得到fff有右逆元⟺∀x∈P,f(x,x)≠0⟺f\iff\forall x\in P, f(x,x)\ne0\iff f⟺∀x∈P,f(x,x)=0⟺f有右逆元.

另外, 由fg=δ,hf=δfg=\delta,hf=\deltafg=δ,hf=δ, 得到g=hg=hg=h.

关联代数中有用的函数

zeta函数

ζ(x,y)=1,∀x,y∈P,x≤y\zeta(x,y)=1,\forall x,y\in P, x\le yζ(x,y)=1,∀x,y∈P,x≤y. 所以有

ζ2(x,y)=∑x≤z≤y1=card[x,y],ζk(x,y)=∑x=x0≤x1≤⋯≤xk=y1,\begin{aligned} \zeta^2(x,y)&=\sum_{x\le z\le y}1=\text{card}[x,y],\\[5pt] \zeta^k(x,y)&=\sum_{x=x_0\le x_1\le\cdots \le x_k= y}1, \end{aligned} ζ2(x,y)ζk(x,y)=x≤z≤y∑1=card[x,y],=x=x0≤x1≤⋯≤xk=y∑1,

即从xxx到yyy的长度为kkk的可重链的条数. 类似有

(ζ−1)(x,y)={1,x<y,0,x=y.(\zeta-1)(x,y)=\begin{cases} 1,&x<y,\\ 0,&x=y. \end{cases} (ζ−1)(x,y)={1,0,x<y,x=y.

于是(ζ−1)k(x,y)(\zeta-1)^k(x,y)(ζ−1)k(x,y)是从xxx到yyy的长度为kkk的链x=x0<x1<⋯<xk=yx=x_0< x_1<\cdots < x_k= yx=x0<x1<⋯<xk=y的条数.

下面是(2−ζ)(x,y)∈I(P)(2-\zeta)(x,y)\in I(P)(2−ζ)(x,y)∈I(P),

(2−ζ)(x,y)={1,x=y,−1,x<y.(2-\zeta)(x,y)=\begin{cases} 1,&x=y,\\ -1,&x<y. \end{cases} (2−ζ)(x,y)={1,−1,x=y,x<y.

Möbius反演

由上述讨论, 局部有限偏序集PPP的zeta函数ζ\zetaζ可逆, 其逆称为PPP的Möbius函数, 记为μ\muμ(或者μP\mu_PμP). 通过归纳定义, 可得到:

μζ=δ⟺{μ(x,x)=1,∀x∈P,μ(x,y)=−∑x≤z<yμ(x,z),∀x<y∈P,\mu\zeta=\delta\iff\\[5pt] \begin{cases} \mu(x,x)=1,\quad\forall x\in P, \\[5pt] \mu(x,y)=-\sum\limits_{x\le z<y}\mu(x,z),\ \forall x<y\in P, \end{cases} μζ=δ⟺⎩⎨⎧μ(x,x)=1,∀x∈P,μ(x,y)=−x≤z<y∑μ(x,z), ∀x<y∈P,

第二个式子可以直接通过(1)(1)(1)式代入后展开得到.

Möbius反演公式

设PPP为所有主序理想有限的偏序集, 令f,g:P→Cf,g: P\to\mathbb Cf,g:P→C, 有

g(x)=∑y≤xf(y),∀x∈P,(2)g(x)=\sum_{y\le x}f(y),\quad\forall x\in P,\tag2 g(x)=y≤x∑f(y),∀x∈P,(2)

当且仅当

f(x)=∑y≤xg(y)μ(y,x),∀x∈P.f(x)=\sum_{y\le x}g(y)\mu(y,x),\quad \forall x\in P. f(x)=y≤x∑g(y)μ(y,x),∀x∈P.

这个证明看原版英文书中有一个通过平凡计算证明的方法, 感觉要更好理解一些.(子空间作用有点抽象) 假定(2)(2)(2)成立, 则有

∑y≤xg(y)μ(y,x)=∑y≤xμ(y,x)∑z≤yf(z)=∑z≤xf(z)∑z≤y≤xμ(y,x)=∑z≤xf(z)δ(z,x)=f(x)\begin{aligned} \sum_{y\le x}g(y)\mu(y,x)&=\sum_{y\le x}\mu(y,x)\sum_{z\le y}f(z)\\ &=\sum_{z\le x}f(z)\sum_{z\le y \le x}\mu(y,x)\\ &=\sum_{z \le x}f(z)\delta(z,x)=f(x) \end{aligned} y≤x∑g(y)μ(y,x)=y≤x∑μ(y,x)z≤y∑f(z)=z≤x∑f(z)z≤y≤x∑μ(y,x)=z≤x∑f(z)δ(z,x)=f(x)

其中倒数第二个等号成立是因为:

δ(z,x)=(ζμ)(z,x)=∑z≤y≤xζ(z,y)μ(y,x)=∑z≤y≤xμ(y,x)\delta(z,x)=(\zeta\mu)(z,x)=\sum_{z\le y\le x}\zeta(z,y)\mu(y,x)=\sum_{z\le y\le x}\mu(y,x) δ(z,x)=(ζμ)(z,x)=z≤y≤x∑ζ(z,y)μ(y,x)=z≤y≤x∑μ(y,x)

对偶形式

设PPP为一个所有主对偶序理想VxV_xVx均有限的偏序集, 令f,g∈CPf,g\in \mathbb C^Pf,g∈CP, 则有

g(x)=∑y≥xf(y),∀x∈P,g(x)=\sum_{y\ge x}f(y),\quad \forall x\in P, g(x)=y≥x∑f(y),∀x∈P,

当且仅当

f(x)=∑y≥xμ(x,y)g(y),∀x∈P.f(x)=\sum_{y\ge x}\mu(x,y)g(y), \quad \forall x\in P. f(x)=y≥x∑μ(x,y)g(y),∀x∈P.

一个例子: Möbius反演公式的意义

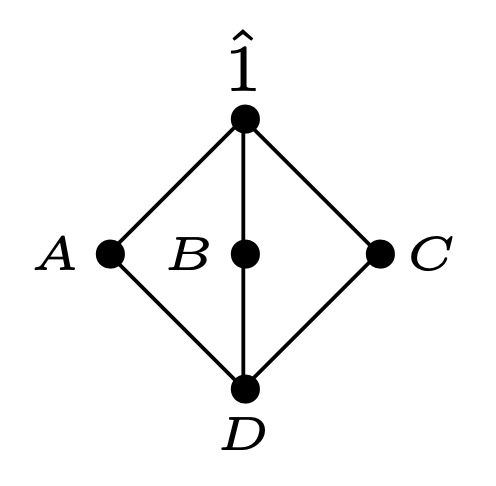
回忆本章开头的一个例子: 有限集合A,B,C,DA,B,C,DA,B,C,D, 满足:

D=A∩B=A∩C=B∩C=A∩B∩C,D=A\cap B=A\cap C=B\cap C=A\cap B\cap C, D=A∩B=A∩C=B∩C=A∩B∩C,

通过容斥原理得到:

∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣=∣A∣+∣B∣+∣C∣−2∣D∣\begin{aligned} |A\cup B\cup C|&=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\\ &=|A|+|B|+|C|-2|D| \end{aligned} ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣=∣A∣+∣B∣+∣C∣−2∣D∣

下面通过Möbius反演解释上述等式:

给定nnn个有限集合S1,...,SnS_1,...,S_nS1,...,Sn, 令PPP为它们所有的交集在包含关系下构成的偏序集, 其中包括空交S1∪⋯∪Sn=1^S_1\cup\cdots\cup S_n=\hat1S1∪⋯∪Sn=1^, 若T∈PT\in PT∈P, 令f(T)f(T)f(T)表示PPP中属于TTT但不属于任何T′<TT'<TT′<T的元素的个数, 令g(T)=∣T∣g(T)=|T|g(T)=∣T∣.

下面通过上述的反演公式找出关于

∣S1∪⋯∪Sn∣=∑T≤1^f(T)=g(1^),|S_1\cup\cdots\cup S_n|=\sum_{T\le \hat1}f(T)=g(\hat1), ∣S1∪⋯∪Sn∣=T≤1^∑f(T)=g(1^),

的表达式, 已知:

g(T)=∑T′≤Tf(T′),g(T)=\sum_{T'\le T}f(T'), g(T)=T′≤T∑f(T′),

由PPP上的Möbius反演得到

0=f(1^)=∑T∈Pg(T)μ(T,1^)=∑T≤1^g(T)μ(T,1^)=g(1^)μ(1^,1^)+∑T<1^∣T∣μ(T,1^)⇒g(1^)=−∑T<1^∣T∣μ(T,1^).\begin{aligned} 0=f(\hat1)&=\sum_{T\in P}g(T)\mu(T,\hat1)\\ &=\sum_{T\le \hat1}g(T)\mu(T,\hat1)\\ &=g(\hat1)\mu(\hat1,\hat1)+\sum_{T< \hat1}|T|\mu(T,\hat1)\\ \Rightarrow g(\hat1)&=-\sum_{T<\hat1}|T|\mu(T,\hat1). \end{aligned} 0=f(1^)⇒g(1^)=T∈P∑g(T)μ(T,1^)=T≤1^∑g(T)μ(T,1^)=g(1^)μ(1^,1^)+T<1^∑∣T∣μ(T,1^)=−T<1^∑∣T∣μ(T,1^).

于是, 上面的例子就可以直接由反演公式给出(Hasse图如下), 其中

0=δ(A,1^)=(μζ)(A,1^)=∑A≤z≤1^μ(A,z)ζ(z,1^)=μ(A,A)ζ(A,1^)+μ(A,1^)ζ(1^,1^)=1+μ(A,1^)⇒μ(A,1^)=μ(B,1^)=μ(C,1^)=−1\begin{aligned} 0&=\delta(A,\hat1)=(\mu\zeta)(A,\hat1)\\ &=\sum_{A\le z\le \hat1}\mu(A,z)\zeta(z,\hat1)\\ &=\mu(A,A)\zeta(A,\hat1)+\mu(A,\hat1)\zeta(\hat1,\hat1)=1+\mu(A,\hat1)\\[5pt] \Rightarrow& \mu(A,\hat1)=\mu(B,\hat1)=\mu(C,\hat1)=-1 \end{aligned} 0⇒=δ(A,1^)=(μζ)(A,1^)=A≤z≤1^∑μ(A,z)ζ(z,1^)=μ(A,A)ζ(A,1^)+μ(A,1^)ζ(1^,1^)=1+μ(A,1^)μ(A,1^)=μ(B,1^)=μ(C,1^)=−1

0=δ(D,1^)=(μζ)(D,1^)=∑D≤z≤1^μ(D,z)ζ(z,1^)=μ(D,D)ζ(D,1^)+μ(D,A)ζ(A,1^)+μ(D,B)ζ(B,1^)+μ(D,C)ζ(C,1^)+μ(D,1^)ζ(1^,1^)=1+(−3)+μ(D,1^)⇒μ(D,1^)=2\begin{aligned} 0&=\delta(D,\hat1)=(\mu\zeta)(D,\hat1)\\ &=\sum_{D\le z\le \hat1}\mu(D,z)\zeta(z,\hat1)\\ &=\mu(D,D)\zeta(D,\hat1)+\mu(D,A)\zeta(A,\hat1)+\mu(D,B)\zeta(B,\hat1)\\ &+\mu(D,C)\zeta(C,\hat1)+\mu(D,\hat1)\zeta(\hat1,\hat1)\\ &=1+(-3)+\mu(D,\hat1)\\[5pt] \Rightarrow& \mu(D,\hat1)=2 \end{aligned} 0⇒=δ(D,1^)=(μζ)(D,1^)=D≤z≤1^∑μ(D,z)ζ(z,1^)=μ(D,D)ζ(D,1^)+μ(D,A)ζ(A,1^)+μ(D,B)ζ(B,1^)+μ(D,C)ζ(C,1^)+μ(D,1^)ζ(1^,1^)=1+(−3)+μ(D,1^)μ(D,1^)=2

组合学笔记(六)局部有限偏序集的关联代数,Möbius反演公式相关推荐

高等组合学笔记(六): 第二类Stirling数,第一类Stirling数以及生成函数
集合的分类定理: nnn元集合NNN的分类μ=(A1,A2,⋯,Am)\mu=(A_1,A_2,\cdots,A_m)μ=(A1,A2,⋯,Am), (∣Ai∣=ai|A_i|=a_i∣Ai ...
组合学笔记(一)偏序集概念与应用
tags: Combinatorics 写在前面最近看论文需要用到偏序集的有关概念, 在这里先梳理一下, 方便以后的使用. 主要参考的书籍是Stanley的经典名著<计数组合学(第一卷)> ...
吴恩达《机器学习》学习笔记六——过拟合与正则化
吴恩达<机器学习>学习笔记六--过拟合与正则化一. 过拟合问题 1.线性回归过拟合问题 2.逻辑回归过拟合问题 3.过拟合的解决二. 正则化后的代价函数 1.正则化思想 2.实际使用的 ...
【K210】K210学习笔记六——MaixHub在线模型训练识别数字
[K210]K210学习笔记六--MaixHub在线模型训练识别数字前言 K210准备工作数据的获取 MaixHub如何在线训练模型训练模型在K210上的测试小结前言本人大四学生,电赛生涯 ...
【组合数学】组合存在性定理 ( 三个组合存在性定理 | 有限偏序集分解定理 | Ramsey 定理 | 相异代表系存在定理 | Ramsey 定理内容概要 )
文章目录一.组合存在性定理二.Ramsey 定理内容概要一.组合存在性定理组合存在性定理主要有三个定理 , 有限偏序集分解定理 , Ramsey 定理 , 相异代表系存在定理 ; 1. 有限 ...
Ethernet/IP 学习笔记六
Ethernet/IP 学习笔记六 EtherNet/IP defines two primary types of communications: explicit and implicit (Ta ...
高等组合学笔记--完结篇
忙忙碌碌一学期, 学完了高等组合学, 虽然课本是一本1974年出版的书, 但是还是能给我很大的启发的(也不知道以后会不会走上这条路). 关于笔记, 其实这之中有很多次想要放弃的, 因为敲公式真的很费时 ...
ROS学习笔记六：理解ROS服务和参数
ROS学习笔记六:理解ROS服务和参数主要介绍ROS服务和参数,同时使用命令行工具rosservice和rosparam. ROS service service是节点之间互相通信的另一种方式,se ...
《MFC游戏开发》笔记六图像双缓冲技术：实现一个流畅的动画
本系列文章由七十一雾央编写,转载请注明出处. http://blog.csdn.net/u011371356/article/details/9334121 作者:七十一雾央新浪微博:http:// ...

组合学笔记(六)局部有限偏序集的关联代数,Möbius反演公式