tags: Combinatorics

写在前面

最近看论文需要用到偏序集的有关概念, 在这里先梳理一下, 方便以后的使用. 主要参考的书籍是Stanley的经典名著《计数组合学(第一卷)》.

下面若不特别指明, 均用PPP代表偏序集.

定义

偏序集(partially-ordered set, poset)PPP是一个集合, 连同一个记为≤\leq≤(≤P\leq_P≤P)的二元关系, 满足下面的三条公理:

对所有的x∈Px\in Px∈P, x≤xx\leq xx≤x(自反性).
如果x≤yx\leq yx≤y 且y≤xy\leq xy≤x, 则x=yx=yx=y(反对称性).
如果x≤yx\leq yx≤y且y≤zy\leq zy≤z, 则x≤zx\leq zx≤z(传递性).

偏序集PPP中的两个元素x,yx,yx,y可比, 如果x≤yx\leq yx≤y或者y≤xy\leq xy≤x, 否则称其为不可比的.
偏序集P,QP,QP,Q同构:
P,QP,QP,Q之间存在一个保持序关系的双射ϕ:P⟶Q\phi:\ P\longrightarrow Qϕ: P⟶Q使得他的逆也保持序关系. 即:
在P中x≤y⟺在Q中ϕ(x)≤ϕ(y).在P中x\leq y\iff 在Q中\phi(x)\leq\phi(y). 在P中x≤y⟺在Q中ϕ(x)≤ϕ(y).

弱子偏序集: 偏序集PPP的子集QQQ连同QQQ上满足"如果在QQQ中有x≤yx\leq yx≤y, 则在PPP中x≤yx\leq yx≤y"的偏序关系, 则QQQ为PPP的弱子偏序集.
加细: 若QQQ是PPP的弱子偏序集, 且作为集合有P=QP=QP=Q, 则称PPP是QQQ的加细.
诱导子偏序集: PPP的子集连同QQQ上的偏序关系:“∀x,y∈Q\forall x,y\in Q∀x,y∈Q, 在QQQ中有x≤y⟺x\leq y\iffx≤y⟺在PPP中有x≤yx\leq yx≤y”.
诱导序: QQQ是PPP的诱导子偏序集, 则QQQ具有诱导序. 有限偏序集PPP恰好有2∣P∣2^{|P|}2∣P∣个诱导子偏序集.
局部有限偏序集: 偏序集PPP的任一区间都是有限的. (可完全由其覆盖关系所确定)
凸子偏序集: 若在偏序集PPP中有x<y<zx<y<zx<y<z且x,z∈Qx,z\in Qx,z∈Q, 就有y∈Qy\in Qy∈Q, 此时区间也是凸的.

yyy覆盖xxx: 设x,y∈Px,y\in Px,y∈P, 若x<yx<yx<y且不存在z∈Pz\in Pz∈P使得x<z<yx<z<yx<z<y. 充要条件:x<yx<yx<y且[x,y]={x,y}[x,y]=\{x,y\}[x,y]={x,y}.
(有限偏序集的)Hasse图: 顶点为PPP中元素, 边为覆盖关系, 并且若x<yx<yx<y则yyy绘制在xxx"上面"的图形.

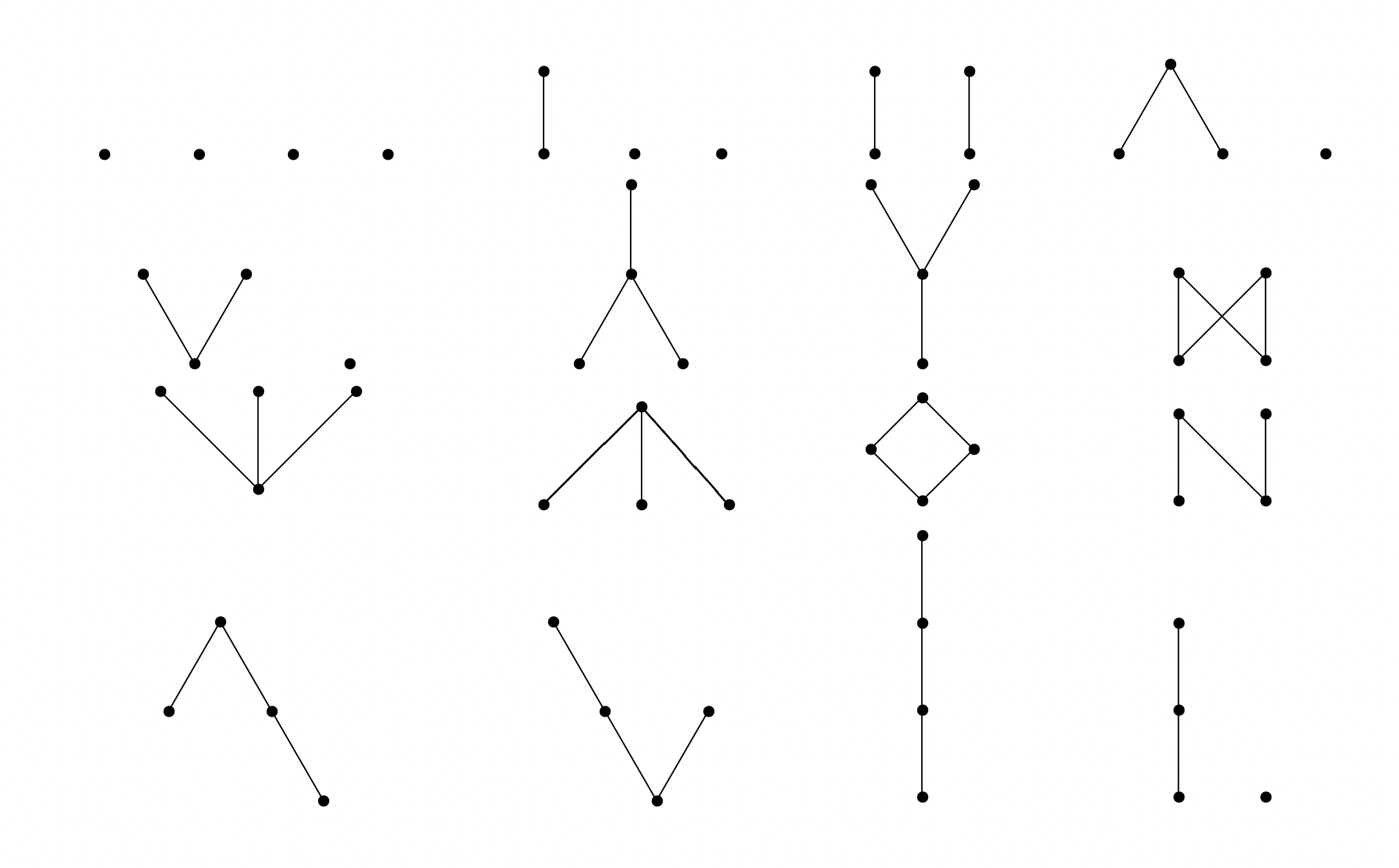
Hasse图的一些例子, 可以参考我的前面的博客. 含有四个元素的偏序集有16个, Hasse图如下图所示

偏序集PPP具有0^\hat 00^: 若存在某个元素0^∈P\hat0\in P0^∈P使得对所有的x∈Px\in Px∈P都有x≥0^x\geq \hat0x≥0^.
偏序集PPP具有1^\hat 11^: 若存在某个元素1^∈P\hat1\in P1^∈P使得对所有的x∈Px\in Px∈P都有x≤1^x\leq \hat1x≤1^.
P^\hat PP^: 表示在PPP中加入0^,1^\hat0,\hat10^,1^得到的偏序集(不管PPP本身是否含有0^\hat00^和1^\hat11^).

若x,y∈Px,y\in Px,y∈P, 那么x,yx,yx,y的上界为满足z≥x,z≥yz\geq x,z\geq yz≥x,z≥y的元素z∈Pz\in Pz∈P.
x,yx,yx,y的最小上界为x,yx,yx,y的上界zzz, 使得对x,yx,yx,y的每一个上界www, 都有w≥zw\geq zw≥z.
若x,yx,yx,y最小上界存在, 则唯一, 记为x∨yx\vee yx∨y, 同理, 最大下界记为x∧yx\wedge yx∧y.
格(lattice): 是一个偏序集LLL, 其中每一对元素的最小上界和最大下界都存在.
格满足的一些性质:
{a.运算∨,∧是结合,交换,幂等的b.x∧(x∨y)=x=x∨(x∧y)c.x∧y=x⟺x∨y=y⟺x≤y\begin{cases}a.运算\vee,\wedge是结合,交换,幂等的\\b. x\wedge(x\vee y)=x=x\vee(x\wedge y)\\c. x\wedge y=x\iff x\vee y=y\iff x\leq y\end{cases} ⎩⎪⎨⎪⎧a.运算∨,∧是结合,交换,幂等的b.x∧(x∨y)=x=x∨(x∧y)c.x∧y=x⟺x∨y=y⟺x≤y

链(chain, 全序集,线性序集)

指任意两个元素都可以比较大小的偏序集. 例如[n]=1,2,...,n[n]={1,2,...,n}[n]=1,2,...,n及其上的普通序关系, 记为n\mathbf {n}n.
偏序集PPP的子集CCC为链, 若CCC 作为PPP的子偏序集的时候是链.
偏序集PPP中的链CCC为饱和的(不可加细的), 如果不存在z∈P−Cz\in P-Cz∈P−C使得对于CCC中某两个元素x,yx,yx,y有x<z<yx<z<yx<z<y, 并且C∪{z}C\cup\{z\}C∪{z}仍然构成链. (有点像上确界的定义, 没办法再塞进去一个元素)
局部有限偏序集中的链x0<x1<⋯<xnx_0<x_1<\cdots<x_nx0<x1<⋯<xn是饱和的, ⟺\iff⟺对1≤i≤n1\leq i\leq n1≤i≤n有xix_ixi覆盖xi−1x_{i-1}xi−1.
有限链的长度ℓ(C):=ℓ(C)=∣C∣−1\ell(C):=\ell(C)=|C|-1ℓ(C):=ℓ(C)=∣C∣−1.
★\bigstar★有限偏序集PPP的长度(秩)定义为ℓ(P):=max⁡{ℓ(C):C为P的链}\ell(P):=\max\{\ell(C):\ C为P的链\}ℓ(P):=max{ℓ(C): C为P的链}.
偏序集的区间[x,y][x,y][x,y]的长度记为ℓ(x,y)\ell(x,y)ℓ(x,y).
★\bigstar★秩为nnn的分次偏序集: 若偏序集PPP的所有极大链都具有相同长度nnn. 此时存在唯一秩函数ρ:P⟶{0,1,...,n}\rho:P\longrightarrow\{0,1,...,n\}ρ:P⟶{0,1,...,n}, 满足:
1. 若xxx是PPP的极小元, 则ρ(x)=0\rho(x)=0ρ(x)=0;
2. 若在PPP中有yyy覆盖xxx, 则ρ(y)=ρ(x)+1\rho(y)=\rho(x)+1ρ(y)=ρ(x)+1.
如果ρ(x)=i\rho(x)=iρ(x)=i, 称元素xxx具有秩iii.
★\bigstar★偏序集的秩生成函数: 对秩为nnn的分次偏序集PPP, 其中有pip_ipi个元素的秩为iii, 则PPP的秩生成函数为:
F(P,q)=∑i=0npiqi.F(P,q)=\sum_{i=0}^np_iq^i. F(P,q)=i=0∑npiqi.
偏序集的可重链: 具有重复元素的链, 即基集为PPP的某个链的可重集合.
反链(Sperner族, 集群): 偏序集PPP的子集AAA, 其中任意两个不同元素不可比较.

序理想

PPP的序理想(半理想, 下集, 下降子集): 满足下列条件的PPP的子集. (有点像左开右闭区间)
若x∈I且y≤x,则y∈I.若x\in I 且 y\leq x, 则y\in I. 若x∈I且y≤x,则y∈I.
对偶序理想(滤子): 满足下列条件的PPP的子集. (有点像左闭右开区间)
若x∈I且y≥x,则y∈I.若x\in I 且 y\geq x, 则y\in I. 若x∈I且y≥x,则y∈I.
偏序集PPP有限时, PPP的反链AAA和序理想III之间存在一一对应.
也就是说, AAA为III的极大元构成的集合, 而
I={x∈P:对某个y∈A有x≤y}.(*)I=\{x\in P:\ 对某个y\in A有x\leq y\}.\tag{*} I={x∈P: 对某个y∈A有x≤y}.(*)
偏序集PPP的所有序理想按照包含关系排序, 构成一个偏序集, 记为J(P)J(P)J(P).
AAA生成III: 若序理想III和极大元所成集合AAA之间满足(∗)(*)(∗)式. 若A={x1,...,xk}A=\{x_1,...,x_k\}A={x1,...,xk}, 记I=⟨x1,...,xk⟩I=\langle x_1,...,x_k\rangleI=⟨x1,...,xk⟩为由AAA生成的序理想.
主序理想: 序理想⟨x⟩\langle x\rangle⟨x⟩为由xxx生成的主序理想, 记为AxA_xAx.
主对偶序理想: Vx={y∈P:y≥x}V_x=\{y\in P:\ y\geq x\}Vx={y∈P: y≥x}表示由xxx生成的主对偶序理想.

偏序集上的运算

直和(不交并): 即定义在P∪QP\cup QP∪Q上的偏序集, 记为P+QP+QP+Q, 指两不相交集合P,QP,QP,Q上定义的偏序集, 使得在P+QP+QP+Q中有x≤yx\leq yx≤y.
- 即在P+QP+QP+Q中, 或者有∀x,y∈P,x≤Py\forall x,y\in P,x\leq_P y∀x,y∈P,x≤Py, 或者有∀x,y∈Q,x≤Qy\forall x,y\in Q,x\leq_Q y∀x,y∈Q,x≤Qy.
- 若一个偏序集不是两个非空偏序集的不交并, 这称之为连通的.
- PPP 和自身的nnn次不交并记为nPnPnP.
- 一个nnn元反链同构于n1n\mathbf{1}n1.
有序和: 即定义在P∪QP\cup QP∪Q上的偏序集记为P⊕QP\oplus QP⊕Q, 使得在P⊕QP\oplus QP⊕Q中x≤yx\leq yx≤y.
- 即在P⊕QP\oplus QP⊕Q中, 或者有∀x,y∈P,x≤Py\forall x,y\in P,x\leq_P y∀x,y∈P,x≤Py, 或者有∀x,y∈Q,x≤Qy\forall x,y\in Q,x\leq_Q y∀x,y∈Q,x≤Qy, 或者有x∈P,y∈Qx\in P,y\in Qx∈P,y∈Q.
- 一条nnn元链由n=1⊕1⊕⋯⊕1⏟n个\bf n=\underbrace{1\oplus1\oplus\cdots\oplus1}_{\mathrm n\text{个}}n=n个1⊕1⊕⋯⊕1给出.
- 串并联偏序集: 在161616个四元偏序集中, 恰有一个是不能由偏序集1\bf11通过直和运算与有序和运算构造出来.
  
  这个偏序集为上图中的第二行的最后一个, 显然他不能够通过直和以及有序和运算生成.
直积(笛卡尔积): 定义在集合{(x,y):x∈P,y∈Q}\{(x,y):\ x\in P,y\in Q\}{(x,y): x∈P,y∈Q}上的偏序集P×QP\times QP×Q, 满足在P×QP\times QP×Q中有(x,y)≤(x′,y′)(x,y)\leq (x',y')(x,y)≤(x′,y′).
- 即∀x,x′∈P,x≤Px′\forall x,x'\in P,x\leq_P x'∀x,x′∈P,x≤Px′, ∀y,y′∈Q,y≤Qy′\forall y,y'\in Q,y\leq_Q y'∀y,y′∈Q,y≤Qy′.
- PPP和它自身的nnn次直积记为PnP^nPn.
- P×Q≅Q×PP\times Q\cong Q\times PP×Q≅Q×P.
- 如果P,QP,QP,Q是分次的且秩生成函数为F(P,q)F(P,q)F(P,q)和F(Q,q)F(Q,q)F(Q,q), 则P×QP\times QP×Q也是分次的且:
  F(P×Q,q)=F(P,q)F(Q,q).F(P\times Q,q)=F(P,q)F(Q,q). F(P×Q,q)=F(P,q)F(Q,q).
有序积: P⊗QP\otimes QP⊗Q, 定义在{(x,y):x∈P,y∈Q}\{(x,y):\ x\in P,y\in Q\}{(x,y): x∈P,y∈Q}上, 满足(x,y)≤(x′,y′)(x,y)\leq (x',y')(x,y)≤(x′,y′), 若x=x′x=x'x=x′且y≤y′y\leq y'y≤y′, 或x<x′x<x'x<x′.
- 如果P,QP,QP,Q是分次的并且QQQ的秩为rrr, 则对于有序积, 有
  F(P⊗Q,q)=F(P,qr+1)F(Q,q).F(P\otimes Q,q)=F(P,q^{r+1})F(Q,q). F(P⊗Q,q)=F(P,qr+1)F(Q,q).
对偶: 记为P∗{P^*}P∗, 是与PPP定义在同一集合上的偏序集P∗P^*P∗, 但在P∗P^*P∗中x≤P∗y⟺y≤Pxx\leq_{P^*} y\iff y\leq_P xx≤P∗y⟺y≤Px.
- 自对偶: P≅P∗P\cong P^*P≅P∗.
  - 下面是所有含四个元素的偏序集中的自对偶图
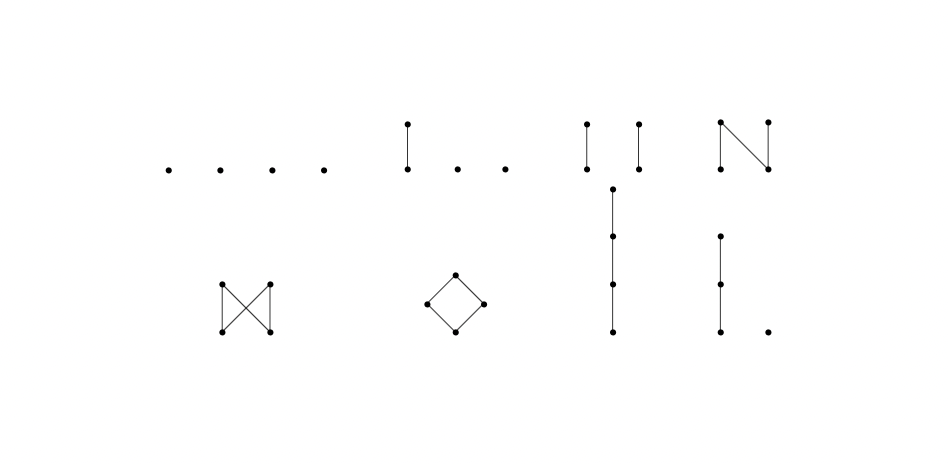
  - 这里是所有含有四个元素的偏序集中的非自对偶偏序集, 共有8个, 显然这些偏序集的对偶都是成对出现的

格(lattice)

格是这样一类偏序集: 其中每一对元素的最小上界和最大下界都存在的偏序集.

子集格

n∈Nn\in \mathbb{N}n∈N, [n][n][n]的所有子集的集合2[n]2^{[n]}2[n]构成偏序集BnB_nBn, 称为子集格.

因子格

n∈Pn\in \mathbb Pn∈P,(P\mathbb PP为正整数) 定义i≤ji\leq ji≤j, 若jjj可以被iii整除, 记为i∣ji\,|\,ji∣j, nnn的所有正整数因子以"自然的"方式成为一个偏序集DnD_nDn.

组合学笔记(一)偏序集概念与应用相关推荐

Docker:学习笔记(1)——基础概念
Docker:学习笔记(1)--基础概念 Docker是什么软件开发后,我们需要在测试电脑.客户电脑.服务器安装运行,用户计算机的环境各不相同,所以需要进行各自的环境配置,耗时耗力.为了解决这个问题 ...
HTML/CSS学习笔记01【概念介绍、基本标签】
w3cschool菜鸟教程.CHM(腾讯微云):https://share.weiyun.com/c1FaX6ZD HTML/CSS学习笔记01[概念介绍.基本标签.表单标签][day01] HTML ...
高等组合学笔记--完结篇
忙忙碌碌一学期, 学完了高等组合学, 虽然课本是一本1974年出版的书, 但是还是能给我很大的启发的(也不知道以后会不会走上这条路). 关于笔记, 其实这之中有很多次想要放弃的, 因为敲公式真的很费时 ...
清华大学邓俊辉-数据结构MOOC笔记-树的概念及逻辑表示
清华大学邓俊辉-数据结构MOOC笔记-树的概念及逻辑表示有关概念: 与图论略有不同,数据结构中的树:1.需要为每一颗树指定一个特殊的顶点,作为"根"(root),对应rooted ...
网络流算法学习笔记——最大流问题基本概念和Ford-Fulkerson方法（标号法C++实现）
屈婉玲<算法设计与分析>第2版第7章网络流算法学习笔记. 基本概念最大流问题,相当于有从s到t的供水系统,每段路径都有限定流量,除了s.t两地外,每个中间点都不能滞留,从s流入多少,就从 ...
程序员面试宝典笔记1-基本概念预处理，const与sizeof
程序员面试宝典笔记1-基本概念&预处理,const与sizeof 基本概念赋值语句: i++: 类型转换运算符问题 a,b交换与比较其他预处理 const sizeof 基本概念赋值 ...
利用计算机技术实现对文本篇章,自然语言处理NLP学习笔记一：概念与模型初探...
前言先来看一些demo,来一些直观的了解. 自然语言处理: 可以做中文分词,词性分析,文本摘要等,为后面的知识图谱做准备. 知识图谱: 还有2个实际应用的例子,加深对NLP的理解九歌机器人: 微软 ...
组合学笔记(六)局部有限偏序集的关联代数,Möbius反演公式
tags: Combinatorics 写在前面前面铺垫了很多偏序集和格,分配格等的基本知识, 下面开始以这些代数结构为研究对象, 探寻其上的一些性质与关系, 我们先以关联代数的定义开始说起. 关联 ...
数据结构-浙大 MOOC 笔记一基本概念
做一些笔记记录自己的学习过程第一节课介绍了数据结构的基本概念,首先没有直接给出相关的定义而是通过思考如何在书架上摆放书籍这样一个简单的类比了解到数据的组织方式的重要性,并通过printN函数的循环实 ...

组合学笔记(一)偏序集概念与应用