好久不见的拉格朗日乘数法

1 引例

我想大多数人对于朗格朗日乘数法的学习已经是好多年前的事情，其中的细节也自然是慢慢模糊了起来，但是对于它的作用我想几乎是不会忘记的，那就是用来求解条件极值。既然大多数人的记忆都停留在这个地方，那么我们就从这个开始重新拾起拉格朗日乘数法。下面就以一个例题来重温一下求解过程：

求解目标函数z=xyz=xyz=xy在约束条件下x+y=1x+y=1x+y=1的条件极值。

解：作拉格朗日函数
F(x,y,λ)=xy+λ(x+y−1)(1)F(x,y,\lambda)=xy+\lambda(x+y-1)\tag 1 F(x,y,λ)=xy+λ(x+y−1)(1)
由式子(1)(1)(1)可得FFF的驻点：
Fx=y+λ=0Fy=x+λ=0Fλ=x+y−1=0(2)\begin{aligned} F_x&=y+\lambda=0\\ F_y&=x+\lambda=0\\ F_{\lambda}&=x+y-1=0 \end{aligned}\tag 2 FxFyFλ=y+λ=0=x+λ=0=x+y−1=0(2)
解方程组(2)(2)(2)便可以求得x,y,λx,y,\lambdax,y,λ：
⟹x=12;y=12;λ=−12\implies x=\frac{1}{2};y=\frac{1}{2};\lambda=-\frac{1}{2} ⟹x=21;y=21;λ=−21
由此我们便可以知道，目标函数z=xyz=xyz=xy在约束条件下x+y=1x+y=1x+y=1的条件极值为z=12∗12=14z=\frac{1}{2}\ast\frac{1}{2}=\frac{1}{4}z=21∗21=41。那为什么可以通过这样的方法来求得条件极值呢？

2 什么是拉格朗日乘数法

在数学优化问题中，拉格朗日乘数法（Lagrange multipliers ）是一种用于求解等式约束条件下局部最小（最大）值的策略。它的基本思想是通过将含约束条件的优化问题转化为无约束条件下的优化问题，以便于得到各个未知变量的梯度，进而求得极值点[1]。因此，一句话就是拉格朗日乘数法是一种用来求解条件极值的工具。那么什么又是条件极值呢?

2.1 条件极值

所谓条件极值是指，在一定约束条件下（通常为方程）目标函数的极值就称为条件极值。

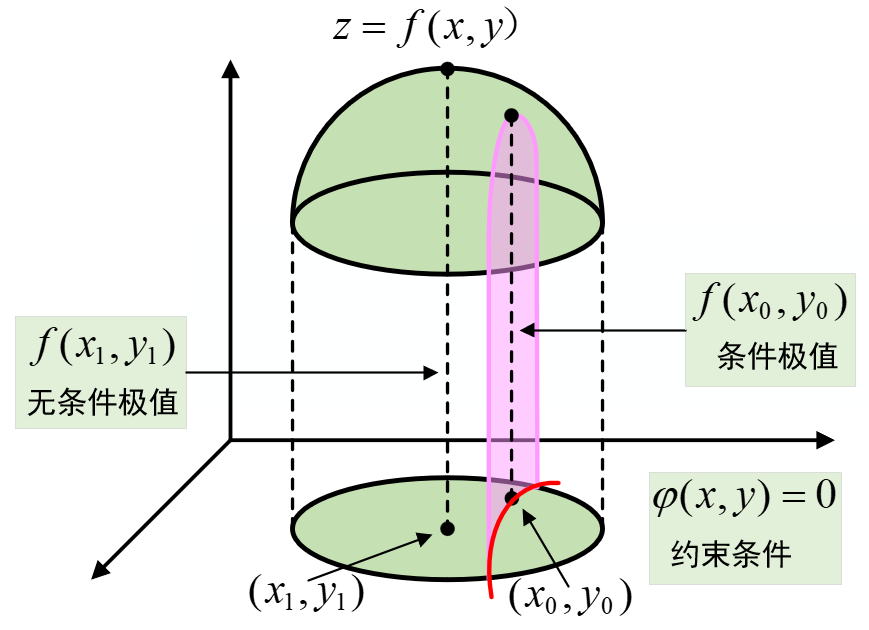
如图所示，函数z=f(x,y)z=f(x,y)z=f(x,y)在其定义域上的极大值（也是最大值）为z=f(x1,y1)z=f(x_1,y_1)z=f(x1,y1)；但如果此时对其施加一个约束条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0，那这就等价的告诉函数z=f(x,y)z=f(x,y)z=f(x,y)极值点同时还要满足约束条件。因此，z=f(x,y)z=f(x,y)z=f(x,y)在约束条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0下的极值点只能在(x0,y0)(x_0,y_0)(x0,y0)处获得（因为此时的φ(x0,y0)=0\varphi(x_0,y_0)=0φ(x0,y0)=0，而φ(x1,y1)≠0\varphi(x_1,y_1)\neq0φ(x1,y1)=0即不满足约束条件）。现在我们已经对条件极值有了一个直观上的理解，那么接下来要探究的就是怎么才能找到这个极值。

2.2 如何求解条件极值

我们知道在一元函数f(x)f(x)f(x)中可以利用极值的必要条件来求解f(x)f(x)f(x)的极值。一元函数极值的必要条件为：若f(x)f(x)f(x)在x=x0x=x_0x=x0处取得极值，且f′(x0)f^{\prime}(x_0)f′(x0)存在，那么立即有f′(x0)=0f^{\prime}(x_0)=0f′(x0)=0。也就是说，我们可以通过令f′(x)=0f^{\prime}(x)=0f′(x)=0来求得极值点x0x_0x0。那如果函数z=f(x,y)z=f(x,y)z=f(x,y)在约束条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0下取得了条件极值f(x0,y0)f(x_0,y_0)f(x0,y0)，那么我们该怎么求解其极值点呢？换句话说条件极值的必要条件是什么呢？

设z0=f(x0,y0)z_0=f(x_0,y_0)z0=f(x0,y0)是z=f(x,y)z=f(x,y)z=f(x,y)在条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0下的条件极值，同时等式φ(x,y)=0\varphi(x,y)=0φ(x,y)=0确定了一个一元隐函数y=y(x)y=y(x)y=y(x)；则此时有一元函数z=f(x,y(x))z=f(x,y(x))z=f(x,y(x))将在x=x0x=x_0x=x0处取得极值。

根据一元函数极值的必要条件有：
dzdx=fx⋅1+fy⋅dydx=0⟹fx(x0,y0)+fy(x0,y0)⋅y′(x0)=0⟹y′(x0)=−fx(x0,y0)fy(x0,y0)(3)\begin{aligned} \frac{dz}{dx}&=f_x\cdot1+f_y\cdot\frac{dy}{dx}=0 \\[1ex] \implies&f_x(x_0,y_0)+f_y(x_0,y_0)\cdot y'(x_0)=0 \\[1ex] \implies &y'(x_0)=-\frac{f_x(x_0,y_0)}{f_y(x_0,y_0)} \end{aligned}\tag 3 dxdz⟹⟹=fx⋅1+fy⋅dxdy=0fx(x0,y0)+fy(x0,y0)⋅y′(x0)=0y′(x0)=−fy(x0,y0)fx(x0,y0)(3)
同时，根据隐函数的求导公式可知：
y′(x0)=−φx(x0,y0)φy(x0,y0)(4)y'(x_0)=-\frac{\varphi_x(x_0,y_0)}{\varphi_y(x_0,y_0)}\tag 4 y′(x0)=−φy(x0,y0)φx(x0,y0)(4)
由式子(3)(4)(3)(4)(3)(4)可得：
fx(x0,y0)fy(x0,y0)=φx(x0,y0)φy(x0,y0)(5)\frac{f_x(x_0,y_0)}{f_y(x_0,y_0)}=\frac{\varphi_x(x_0,y_0)}{\varphi_y(x_0,y_0)}\tag 5 fy(x0,y0)fx(x0,y0)=φy(x0,y0)φx(x0,y0)(5)
由(5)(5)(5)可得：
fx(x0,y0)φx(x0,y0)=fy(x0,y0)φy(x0,y0)(6)\frac{f_x(x_0,y_0)}{\varphi_x(x_0,y_0)}=\frac{f_y(x_0,y_0)}{\varphi_y(x_0,y_0)}\tag 6 φx(x0,y0)fx(x0,y0)=φy(x0,y0)fy(x0,y0)(6)
那么，此时我们便可以理解成{fx(x0,y0),fy(x0,y0)}//{φx(x0,y0),φy(x0,y0)}\{f_x(x_0,y_0),f_y(x_0,y_0)\}//\{\varphi_x( x_0,y_0),\varphi_y( x_0,y_0)\}{fx(x0,y0),fy(x0,y0)}//{φx(x0,y0),φy(x0,y0)}，即目标函数和约束条件在取得条件极值处的梯度平行。由此可知，取得条件极值的必要条件为：Δf(x0,y0)//Δφ(x0,y0)\Delta f(x_0,y_0)//\Delta \varphi(x_0,y_0)Δf(x0,y0)//Δφ(x0,y0)。

由Δf(x0,y0)//Δφ(x0,y0)\Delta f(x_0,y_0)//\Delta \varphi(x_0,y_0)Δf(x0,y0)//Δφ(x0,y0)可知：
∃λ0,使得Δf(x0,y0)=−λ0⋅Δφ(x0,y0)⟹Δf(x0,y0)+λ0⋅Δφ(x0,y0)=0⃗⟹Δ{f(x0,y0)+λ0⋅φ(x0,y0)}=0⃗⟹Δ(f+λ0φ)=0⃗(7)\begin{aligned} \exists \lambda_0,\text{使得}&\Delta f(x_0,y_0)=-\lambda_0\cdot\Delta \varphi(x_0,y_0) \\ \\ \implies&\Delta f(x_0,y_0)+\lambda_0\cdot\Delta \varphi(x_0,y_0) =\vec{0}\\ \\ \implies&\Delta \{f(x_0,y_0)+\lambda_0\cdot\varphi(x_0,y_0)\} =\vec{0}\\ \\ \implies&\Delta(f+\lambda_0\varphi)=\vec{0} \end{aligned}\tag 7 ∃λ0,使得⟹⟹⟹Δf(x0,y0)=−λ0⋅Δφ(x0,y0)Δf(x0,y0)+λ0⋅Δφ(x0,y0)=0Δ{f(x0,y0)+λ0⋅φ(x0,y0)}=0Δ(f+λ0φ)=0(7)
进一步，如果我们令F(x,y,λ)=f(x,y)+λφ(x,y)F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)F(x,y,λ)=f(x,y)+λφ(x,y)，那么由(7)(7)(7)可得ΔF(x0,y0,λ0)=0⃗\Delta F(x_0,y_0,\lambda_0)=\vec{0}ΔF(x0,y0,λ0)=0，即(x0,y0,λ0)(x_0,y_0,\lambda_0)(x0,y0,λ0)是函数F(x,y,λ)F(x,y,\lambda)F(x,y,λ)的驻点。因此，求f(x,y)f(x,y)f(x,y)的条件极值就可以转换为求F(x,y,λ)F(x,y,\lambda)F(x,y,λ)驻点的问题。

同时，我们称F(x,y,λ)=f(x,y)+λφ(x,y)F(x,y,\lambda)=f(x,y)+\lambda\varphi(x,y)F(x,y,λ)=f(x,y)+λφ(x,y)为条件极值的拉格朗日函数，λ\lambdaλ称为拉格朗日乘数。因此，函数f(x,y)f(x,y)f(x,y)在点(x0,y0)(x_0,y_0)(x0,y0)处取得条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0条件下极值的必要条件为：∃λ0\exists\; \lambda_0∃λ0使得(x0,y0,λ0)(x_0,y_0,\lambda_0)(x0,y0,λ0)为拉格朗日函数的F(x,y,λ)F(x,y,\lambda)F(x,y,λ)的驻点。

2.3 拉格朗日乘数法的求解步骤

求多元函数Z=f(x,y,z,...)Z=f(x,y,z,...)Z=f(x,y,z,...)在条件φ(x,y,...)=0,ϕ(x,y,...)=0,...\varphi(x,y,...)=0,\phi(x,y,...)=0,...φ(x,y,...)=0,ϕ(x,y,...)=0,...下的极值：

第一步：作拉格朗日函数
F(x,y,z,...,λ,μ,...)=f(x,y,z,...)+λφ(x,y,...)+μϕ(x,y,...)+...F(x,y,z,...,\lambda,\mu,...)=f(x,y,z,...)+\lambda\varphi(x,y,...)+\mu\phi(x,y,...)+... F(x,y,z,...,λ,μ,...)=f(x,y,z,...)+λφ(x,y,...)+μϕ(x,y,...)+...
第二步：求F(x,y,z,...,λ,μ,...)F(x,y,z,...,\lambda,\mu,...)F(x,y,z,...,λ,μ,...)的驻点(x0,y0,z0,...,λ0,μ0,...)(x_0,y_0,z_0,...,\lambda_0,\mu_0,...)(x0,y0,z0,...,λ0,μ0,...)，即解如下方程组：
{Fx=0Fy=0⋯Fλ=0⋯\begin{aligned} \begin{cases} F_x=0\\ F_y=0\\ \cdots\\ F_\lambda=0\\ \cdots \end{cases} \end{aligned} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧Fx=0Fy=0⋯Fλ=0⋯
第三步：(x0,y0,z0,...,λ0,μ0,...)(x_0,y_0,z_0,...,\lambda_0,\mu_0,...)(x0,y0,z0,...,λ0,μ0,...)便是可能的条件极值点

3 总结

在本篇文章中，笔者首先介绍通过一个引例介绍了如何通过拉格朗日乘数法来求解条件极值；然后通过一元函数极值的必要条件推导出了拉格朗日乘数法的原理；最后再推广得到了如何用拉格朗日乘数法来求解多元函数的条件极值。本次内容就到此结束，感谢阅读！

若有任何疑问与见解，请发邮件至moon-hotel@hotmail.com并附上文章链接，青山不改，绿水长流，月来客栈见！

引用

[1]https://en.wikipedia.org/wiki/Lagrange_multiplier

[2]《高等数学学习手册》徐小湛