Lecture 9 Convex 模型预测控制（MPC）

动机

前面花了两节来讲如何使用各种方法推导LQR问题的解。虽然LQR非常特殊（Cost必须得是二次的，系统方程必须得是线性的），但是即使对于非线性系统（如倒立摆），对于轨迹跟踪任务（对应TVLQR-时变LQR）或稳定任务（对应TILQR-时不变LQR），仍然可以在期望的轨迹处进行线性化，也可以取得不错的控制效果（因为控制率会倾向于让系统一直保持在线性化点附近）。

但是，经典LQR最大的问题就是，无法处理任何在状态 x x x或者输入 u u u上的约束，这会导致：

LQR输出的控制率给到执行器因为执行器饱和无法成功执行，影响系统精度
输出的控制指令太大使系统变得很“大起大落”，不安全
在某些场景中，如四旋翼，当控制指令太大时，如LQR输出一个很大的加速度，则对四旋翼来说意味着需要用一个较大的倾角去达到这个加速度，而简单的四旋翼控制往往是在悬停态线性化的，因此此时会使系统线性化的精度变得很差（离线性化的点太远），LQR输出的控制率不可行。

想要在LQR中加入约束处理的能力，难点有，

在Lecture 8的通过动态规划推导LQR的过程中，得知系统的LQR最优反馈控制率 u u u是由最小化系统的Cost-to-Go函数 V ( x ) V(x) V(x)得到的，这个过程我们实际上是对 V ( x ) V(x) V(x)对 u u u求梯度令其等于0，得到系统的 u u u，因此我们解的是一个不考虑 u u u约束的最小化 V V V的问题来得到 u u u，假如要解一个带 u u u约束的最小化问题，则，此问题无法写出解析解（因为在推导的过程也不知道实际的 u u u会是一个什么约束），也就无法进行下一步的迭代。因此，想要在DP或者Riccati迭代中处理 u u u的约束，是比较困难的（当然可以通过罚函数法或者增广拉格朗日法把约束变成Cost，后文DDP中会讲）。
在DP或者Riccati中，处理 x x x的约束就更难了， x x x在整个推导过程中，不像 u u u那样是直接解最优化方程得到的，而是解出 u u u之后再通过 x 1 x_1 x1前向rollout得到的，因此这个过程很不直接，想要约束 x x x难度更大
但是，假如通过QP来解LQR问题，关于LQR问题中的所有 x u x \ u x u的线性约束都可以转成标准的 C x ≤ d Cx \leq d Cx≤d的标准形式，这样仍然是一个标准的QP问题（虽然要在QP中处理约束了，但是还是有成熟的求解器，我们自己也可以基于增广拉格朗日实现简单的），在求解流程上并无区别。
因此，目前主流的Convex MPC都是通过转化成QP的形式，再利用QP形式KKT系统Hessian矩阵的稀疏性，加速QP过程的求解，也可以做到几千hz

基础概念

凸集（Convex Set）

凸集的定义：集合中任意两个点组成的线段上的点仍然在集合中。常见的凸集有，

线性子空间（ A x = b Ax=b Ax=b）
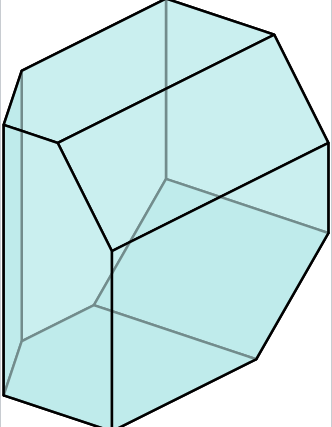
半空间（Half-spaces）、盒子（box）、多面体（Polytopes）（都可以表达成 A x ≤ b Ax \leq b Ax≤b）
椭球( x T P x ≤ 1 x^TPx \leq1 xTPx≤1)
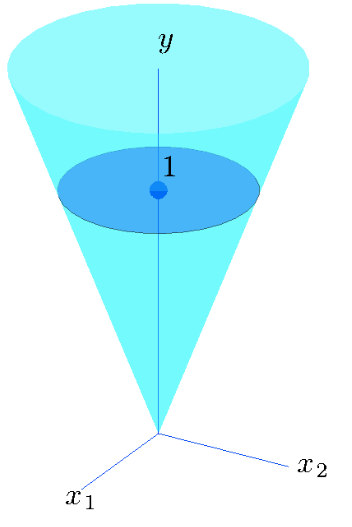
锥体（cone）（ ∣ ∣ x 2 : n ∣ ∣ 2 ≤ x 1 ||x_{2:n}||_2 \leq x_1 ∣∣x2:n∣∣2≤x1，如 x 2 + y 2 < z \sqrt{x^2+y^2}<z x2+y2 <z）。当范数为二范数时，叫做二阶锥体。在机器人应用中，如火箭的推力约束，四足狗的摩擦锥约束，都可以表示成一个二阶锥约束。

Polytopes

cone

注意，对于一个等式约束来说，只有线性的等式约束才是凸集，二次的不是。如将机器人的动力学进行二阶泰勒展开后，则此时的 Δ \Delta Δ系统的等式约束并不是一个凸集。但是工程上可以通过一些trick把二次的等式约束转成不等式约束转化成凸集。

凸函数（Convex Function）

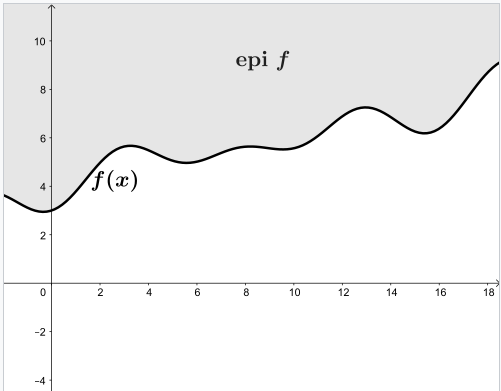
凸函数的定义就是，函数值上面的那一块（epigraph）是凸集。

ps：当我们讨论凸函数时，默认就是个因变量为标量的函数。

常见的凸函数有：

线性函数（ f ( x ) = c T x f(x) = c^T x f(x)=cTx）
二次函数（ f ( x ) = 1 2 x T Q x + q T x , ∋ Q ≥ 0 f(x) = \frac{1}{2} x^T Q x + q^T x, \ni Q \geq 0 f(x)=21xTQx+qTx,∋Q≥0）
范数（ f ( x ) = ∣ x ∣ f(x) = |x| f(x)=∣x∣），所有的范数都是凸函数

凸优化（Convex Optimazation）

凸优化的定义是，在一个凸集中优化一个凸函数。常见的凸优化问题有

线性规划LP（Linear Program）：线性的 f ( x ) f(x) f(x)，线性的 c ( x ) c(x) c(x)
二次规划QP（Quadratic Program）：二次的 f ( x ) f(x) f(x)，线性的 c ( x ) c(x) c(x)
二次约束二次规划QCQP（Quadratic Constraint Quadratic Program）：二次的 f ( x ) f(x) f(x)，二次的 c ( x ) c(x) c(x)
二阶锥规划SOCP（Second-order cone Program）：线性的 f ( x ) f(x) f(x)，二阶锥的 c ( x ) c(x) c(x)

老师说，program is an old school word in optimization.

凸优化的性质：

凸优化没有满足KKT条件的虚假（spurious）局部极小值点，在凸优化中假如找到了满足KKT条件的点，一定是全局最小值点。
在实践中，使用牛顿法可以很可靠和快速地迭代求解出凸优化问题（只要问题不太大，一般5-10次迭代）
凸优化问题可以从理论上保证一个 迭代收敛的时间上界。即，若一个最优控制问题的最终形式是一个凸优化问题，比如可以说，一定最多在50ms内就可以找到一个解，这与通用的非线性优化是不一样的，非线性优化无法bound solution time，可能会一直没有结果。

Convex MPC

再次强调，本节所讲的MPC更多的像是一种LQR，考虑从LQR的角度来加上约束，推导，带约束下的LQR该怎么才能取得一个好的控制率。回顾在DP中，假如通过Backward Pass求出所有无输入约束下的Cost-to-GO V ( x ) V(x) V(x)后，可以通过下式来不断前向rollout得到
u k = arg ⁡ min ⁡ u l ( x k , u ) + V k + 1 ( f ( x k , u ) ) = arg ⁡ min ⁡ u 1 2 u T R k u + 1 2 ( A k x k + B k u ) T P k + 1 ( A k x k + B k u ) (1) \begin{align} u_k &= \arg\min_u l(x_k, u) + V_{k+1}(f(x_k,u)) \\ &= \arg\min_u \frac{1}{2} u^TR_k u + \frac{1}{2} (A_k x_k + B_k u)^TP_{k+1}(A_k x_k + B_k u) \end{align}\tag{1} uk=arguminl(xk,u)+Vk+1(f(xk,u))=argumin21uTRku+21(Akxk+Bku)TPk+1(Akxk+Bku)(1)
那么，很自然地一个想法，可以在前向rollout求解这个最优化问题的过程中加入 u u u的约束，然后我再用QP或者增广拉格朗日法解出满足约束的 u u u，因为这个问题的自变量维度小，也可以很快迭代出结果。但是，这样做效果往往不太好，因为，实际上Backward pass求Cost-to-Go V ( x ) V(x) V(x)时，是没有考虑 u u u约束的，即，这个到终点的Cost函数，是不正确的。

这样做实际上是拿当前点的Cost-to-Go来evaluate控制u，在控制的开始阶段是不合理的（因为开始阶段误差很大，往往 u u u也很大），但是，随着控制的进行，在LQR控制器的作用下（无约束情况），控制的 u u u会越来越小，因此，可以假设，在一段时间之后，随着 u u u的变小， u u u会逐渐满足这种最大值限制，此时由Backward Pass所求得的 V ( x ) V(x) V(x) 会变得准确，我们利用这一点，把带约束的LQR问题写成如下形式，
min ⁡ x 1 : H , u 1 : H − 1 ∑ k = 1 H − 1 1 2 x k Q k x k + 1 2 u k T R k u k + x H T P x H ∋ x k ∈ X u k ∈ U (2) \begin{align} \min_{x_{1:H}, u_{1:H-1}} &\sum_{k=1}^{H-1} \frac{1}{2} x_k Q_k x_k + \frac{1}{2} u_k^T R_k u_k + x_H^T P x_H \\ \ \ni \ x_k &\in X \\ u_k &\in U \end{align}\tag{2} x1:H,u1:H−1min ∋ xkukk=1∑H−121xkQkxk+21ukTRkuk+xHTPxH∈X∈U(2)
这里我们在evaluate控制量 u u u时，我们使用之后 H H H步的 V ( x ) V(x) V(x)，其中 H < N H<N H<N叫做时间窗口（horizon）。

可以看出，当 H = N H=N H=N时，问题变成，用QP直接解带约束的Convex MPC问题，此时计算量较大
当 H = 1 H=1 H=1时，此时问题退化成无约束的LQR，通过这种方式求出的结果是不准的（因为 V n ( x ) = x n T P x n V_n(x)=x_n^TPx_n Vn(x)=xnTPxn不准）
H H H的值是一个由计算量和准确度所取的一个折衷（tradeoff）

平时在使用MPC时，我们更多的不是通过LQR的结果来确定的这个 V ( x ) V(x) V(x)，而是设置一个 Q f i n a l Q_{final} Qfinal，因为问题是使系统状态回到原点，因此，这也算是合理的，即，离原点越远，则Cost-to-Go x T Q f i n a l x x^TQ_{final}x xTQfinalx越大。所以一定要设置一个 Q f i n a l Q_{final} Qfinal，否则问题还是不太准。

案例分析

分析一个平面双旋翼系统，使该双旋翼系统到达特定的状态（如特定的位置）.
m x ¨ = − ( u 1 + u 2 ) sin ⁡ ( θ ) m y ¨ = ( u 1 + u 2 ) cos ⁡ ( θ ) − m g J θ ¨ = 1 2 l ( u 2 − u 1 ) (3) \begin{align} m \ddot x &= -(u_1 + u_2) \sin(\theta) \\ m \ddot y &= (u_1 + u_2) \cos(\theta) - mg \\ J \ddot \theta &= \frac{1}{2} l (u_2 - u_1) \end{align}\tag{3} mx¨my¨Jθ¨=−(u1+u2)sin(θ)=(u1+u2)cos(θ)−mg=21l(u2−u1)(3)
这是个非线性系统（系统动力学存在 u u u与 x x x的耦合），将飞机在悬停状态线性化此时有条件 θ = 0 , u 1 = u 2 = 1 2 m g \theta=0, \ u_1=u_2=\frac{1}{2}mg θ=0, u1=u2=21mg，并假设飞机一直在小角度附近运动，即 θ ≈ 0 \theta \approx 0 θ≈0（在悬停态线性化并不意味着飞机会一直处于这种状态，只是说我们假设飞机一直在悬停态附近运动，飞机仍然可以有 Δ u ， Δ θ \Delta u，\Delta \theta Δu，Δθ 此时线性化的模型是较准的）,对线性化的模型离散化后进行LQR和MPC控制。
KaTeX parse error: Undefined control sequence: \part at position 172: …&\approx \frac{\̲p̲a̲r̲t̲ ̲f_1(x,y,\theta,…

因为系统方程对状态 x , y x,y x,y的导数都为0，在推导中省略了

由于此时问题不再是回到原点，而是到达任意一个状态 x r e f x_{ref} xref，因此式子(2)变为
min ⁡ x 1 : H , u 1 : H − 1 ∑ k = 1 H − 1 [ 1 2 ( x k − x r e f ) T Q k ( x k − x r e f ) + 1 2 u k T R k u k ] + ( x H − x r e f ) T P ( x H − x r e f ) = min ⁡ x 1 : H , u 1 : H − 1 ∑ k = 1 H − 1 [ 1 2 x k T Q k x k + 1 2 u k T R k u k − ( Q k x r e f ) T x k ] + x H T P x H − ( Q H x r e f ) T x H x m i n ≤ x ≤ x m a x u m i n ≤ u ≤ u m a x (5) \begin{align} \min_{x_{1:H}, u_{1:H-1}} &\sum_{k=1}^{H-1} [\frac{1}{2} (x_k-x_{ref})^T Q_k (x_k-x_{ref}) + \frac{1}{2} u_k^T R_k u_k] + (x_H-x_{ref})^T P (x_H-x_{ref}) \\ = \min_{x_{1:H}, u_{1:H-1}} &\sum_{k=1}^{H-1} [\frac{1}{2} x_k^T Q_k x_k + \frac{1}{2} u_k^T R_k u_k - (Q_kx_{ref})^Tx_k] + x_H^T P x_H - (Q_Hx_{ref})^Tx_H \\ &x_{min}\leq x \leq x_{max} \ \ u_{min}\leq u \leq u_{max} \end{align}\tag{5} x1:H,u1:H−1min=x1:H,u1:H−1mink=1∑H−1[21(xk−xref)TQk(xk−xref)+21ukTRkuk]+(xH−xref)TP(xH−xref)k=1∑H−1[21xkTQkxk+21ukTRkuk−(Qkxref)Txk]+xHTPxH−(QHxref)TxHxmin≤x≤xmax umin≤u≤umax(5)
依旧是可以转化成标准的QP问题（这里 Q k = Q R k = R Q_k=Q \ R_k=R Qk=Q Rk=R）。像上一节所做，我们把决策变量堆在一起成 z z z。

在求解问题时，用的是OSQP，取 N = 20 N=20 N=20,因为 d i m ( x ) = 6 d i m ( u ) = 2 dim(x)=6 \ dim(u)=2 dim(x)=6 dim(u)=2（实际上 x x x由 x 2 x_2 x2到 x 21 x_{21} x21是决策变量， u u u由 u 1 u_1 u1到 u 2 0 u_20 u20是决策变量），所以优化变量一共是160维。

由于OSQP只存在不等式约束 l o w e r ≤ D z ≤ u p p e r lower \leq Dz\leq upper lower≤Dz≤upper，因此所有等式约束都要转化成一个不等式约束，其中 l o w e r = u p p e r lower=upper lower=upper。
z = [ u 1 x 2 u 2 . . u 20 x 21 ] ∈ R 160 (5) \begin{align} z = \begin{bmatrix} u_1 \\ x_2 \\ u_2 \\ . \\ . \\ u_{20}\\ x_{21} \end{bmatrix} \in \mathbb R^{160} \end{align}\tag{5} z= u1x2u2..u20x21 ∈R160(5)

H = [ R 0 . . . 0 . 0 0 0 Q . . . 0 . 0 0 . 0 0 . . . Q . 0 0 . . . . . . . . 0 0 0 . . . 0 . R 0 0 0 . . . 0 . 0 P ] ∈ R 160 × 160 (6) \begin{align} H = \begin{bmatrix} R & 0 & ... & 0 & . & 0 & 0\\ 0 & Q & ... & 0 & . & 0& 0\\ \ & \ & . & \ \\ 0 & 0 & ... & Q &. & 0& 0\\ . & . & ... & . &. & . & 0\\ 0 & 0 & ... & 0 &. & R& 0\\ 0 & 0 & ... & 0 &. & 0& P \end{bmatrix} \in \mathbb R^{160 \times 160} \end{align}\tag{6} H= R0 0.000Q 0.00...................00 Q.00......000.R000000P ∈R160×160(6)

其中，约束共有120个状态的等式约束（每条 x k + 1 = A k x k + B u k x_{k+1}=A_kx_k+Bu_k xk+1=Akxk+Buk可以提供 d i m ( x ) dim(x) dim(x)个约束），40个关于输入 u u u的约束（ u u u一共有40个，其中 S u ∈ R 40 × 160 S_u \in \mathbb R^{40 \times 160} Su∈R40×160是选择矩阵，使得 S u z = u S_uz=u Suz=u），20个关于状态 θ \theta θ的约束（其中 S θ ∈ R 20 × 160 S_\theta \in \mathbb R^{20 \times 160} Sθ∈R20×160是选择矩阵，使得 S θ z = θ S_\theta z=\theta Sθz=θ）

在本问题中，轨迹上x(t) 所有点的参考值都是最终的那个目标点，而在作业HW2中，从起点到终点线性插值了一个函数，以插值后的函数用时间索引作为x(t)的参考。并且，问题的规模是一直不变的，一直会从当前时间对应的t往后走N步，就算到了终点也会继续往后，直到收敛。

代码部分：动力学

#Planar Quadrotor Dynamics
function quad_dynamics(x,u) #非线性动力学θ = x[3]ẍ = (1/m)*(u[1] + u[2])*sin(θ)ÿ = (1/m)*(u[1] + u[2])*cos(θ) - gθ̈ = (1/J)*(ℓ/2)*(u[2] - u[1])   # J是转动惯量，l是飞机轴距return [x[4:6]; ẍ; ÿ; θ̈]
end
function quad_dynamics_rk4(x,u)#RK4 integration with zero-order hold on uf1 = quad_dynamics(x, u)f2 = quad_dynamics(x + 0.5*h*f1, u)f3 = quad_dynamics(x + 0.5*h*f2, u)f4 = quad_dynamics(x + h*f3, u)return x + (h/6.0)*(f1 + 2*f2 + 2*f3 + f4)
end
x_hover = zeros(6) #状态包括x y θ以及它们的导数 线性化的点是全0点，所以lb=ub=-A(x-x_linear)=-Ax
u_hover = [0.5*m*g; 0.5*m*g]   #悬停态条件
A = ForwardDiff.jacobian(x->quad_dynamics_rk4(x,u_hover),x_hover);  #代码中投了懒，用自动微分代替了我们手算
B = ForwardDiff.jacobian(u->quad_dynamics_rk4(x_hover,u),u_hover);  #而且它是离散化后再做的线性化
quad_dynamics_rk4(x_hover, u_hover)

控制器代码

#Build QP matrices for OSQP
Nh = 20 #one second horizon at 20Hz horizon决定QP子问题的维度
Nx = 6  #状态维度   #
Nu = 2  #输入维度   #
U = kron(Diagonal(I,Nh), [I zeros(Nu,Nx)])  #选择矩阵S_u 40*160
Θ = kron(Diagonal(I,Nh), [0 0 0 0 1 0 0 0]) #选择矩阵S_θ 20*160
H = sparse([kron(Diagonal(I,Nh-1),[R zeros(Nu,Nx); zeros(Nx,Nu) Q]) zeros((Nx+Nu)*(Nh-1), Nx+Nu); zeros(Nx+Nu,(Nx+Nu)*(Nh-1)) [R zeros(Nu,Nx); zeros(Nx,Nu) P]])
b = zeros(Nh*(Nx+Nu))   #闭环部分会置为-Qx_ref。对应QP中的线性Cost
C = sparse([[B -I zeros(Nx,(Nh-1)*(Nu+Nx))]; zeros(Nx*(Nh-1),Nu) [kron(Diagonal(I,Nh-1), [A B]) zeros((Nh-1)*Nx,Nx)] + [zeros((Nh-1)*Nx,Nx) kron(Diagonal(I,Nh-1),[zeros(Nx,Nu) Diagonal(-I,Nx)])]])
# C矩阵对应公式中D的上半部分，表示系统方程约束
#Dynamics + Thrust limit constraints
D = [C; U]  # D大矩阵，表示所有的等式与不等式约束
lb = [zeros(Nx*Nh); kron(ones(Nh),umin-u_hover)]    #前面120维是系统等式约束，上下界一样
ub = [zeros(Nx*Nh); kron(ones(Nh),umax-u_hover)]    #后面40维是系统输入约束，有上下界#Dynamics + thrust limit + bound constraint on θ to keep the system within small-angle approximation
#D = [C; U; Θ]
#lb = [zeros(Nx*Nh); kron(ones(Nh),umin-u_hover); -0.2*ones(Nh)]
#ub = [zeros(Nx*Nh); kron(ones(Nh),umax-u_hover); 0.2*ones(Nh)]prob = OSQP.Model()
OSQP.setup!(prob; P=H, q=b, A=D, l=lb, u=ub, verbose=false, eps_abs=1e-8, eps_rel=1e-8, polish=1);#MPC Controller
function mpc_controller(t,x,xref)#Update QP problemlb[1:6] .= -A*x #每一次都把QP的初始状态给更新到当前状态ub[1:6] .= -A*x   #因为线性化点是全0点，所以减不减是一样的for j = 1:(Nh-1)b[(Nu+(j-1)*(Nx+Nu)).+(1:Nx)] .= -Q*xref   #更新QP中的线性项endb[(Nu+(Nh-1)*(Nx+Nu)).+(1:Nx)] .= -P*xref  # 轨迹上所有点的目标都是最终的那个位置OSQP.update!(prob, q=b, l=lb, u=ub)#Solve QPresults = OSQP.solve!(prob)Δu = results.x[1:Nu]    #只取第一个u作为系统控制的u，下一次u重新算return u_hover + Δu
end#闭环MPC控制器
function closed_loop(x0,controller,N)xhist = zeros(length(x0),N)u0 = controller(1,x0)uhist = zeros(length(u0),N-1)uhist[:,1] .= u0xhist[:,1] .= x0for k = 1:(N-1)uk = controller(k,xhist[:,k])uhist[:,k] = max.(min.(umax, uk), umin) #enforce control limitsxhist[:,k+1] .= quad_dynamics_rk4(xhist[:,k],uhist[:,k])endreturn xhist, uhist
end

结果：

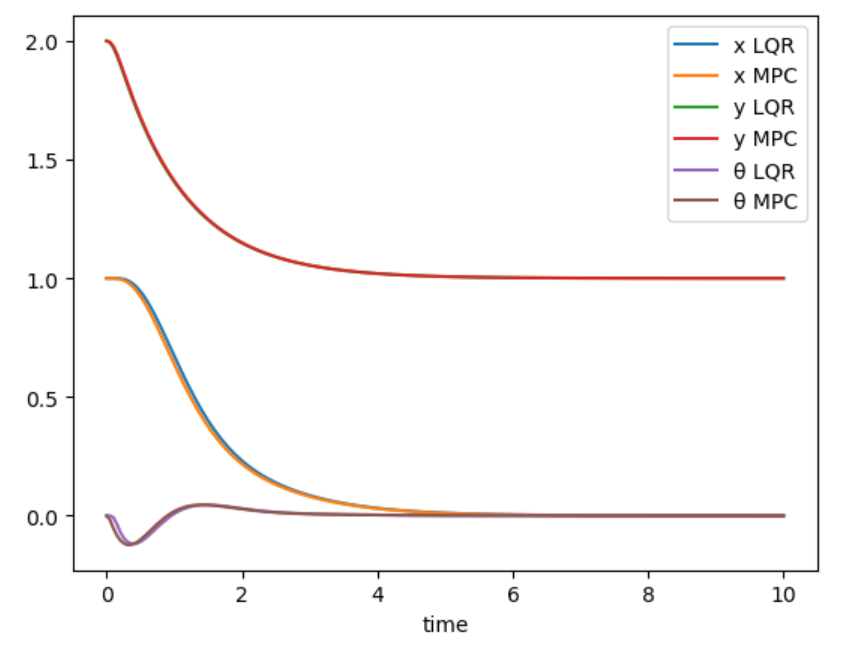
终止状态我们固定为[0.0; 1.0; 0; 0; 0; 0]，分别选取其初始状态[2.0,1.0,0,0,0,0]和[5,2,0,0,0,0]，对该无人机进行LQR和MPC的期望状态跟踪，仿真结果如下。

可以看出，在位置近时，由于LQR和MPC本身不会产生太大的输入 u u u不会违反约束，因此系统都能够很好地跟踪，但是当初始位置离期望位置远地时候，LQR的跟踪结果是发散的，从动图可以看出，因为在使用了LQR输出了一个非常大的u（虽然我们在代码中限制chop了 u u ud的最大和最小值），因为Chop之后造成控制器输出与实际执行不服合，系统发散，而使用MPC则可以很好地解决这个问题。

并且，在给MPC加了倾角 θ \theta θ的最大约束后，可以看出，整个位置跟踪过程飞机可以很好地保持在限制的角度内，虽然速度较慢，但是此时系统离悬停态更近，我们的线性化模型更准，更安全。

初始位置近时状态轨迹

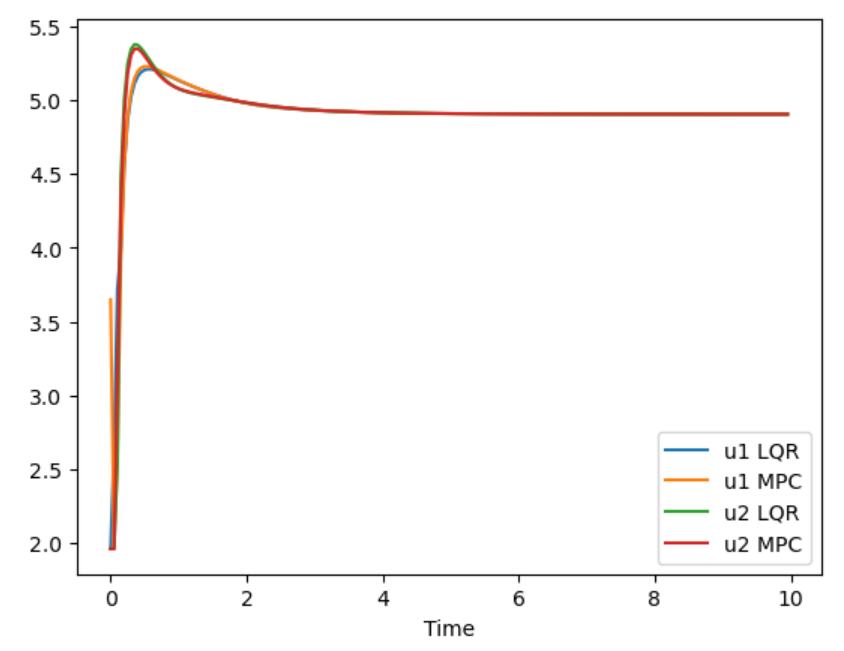初始位置近时输入轨迹

初始位置远时状态轨迹

初始位置远时输入轨迹

初始位置近时仿真	初始位置远时LQR
初始位置远时MPC	初始位置远，状态约束MPC

lecture09 Convex 模型预测控制（MPC）相关推荐

Apollo代码学习(六)—模型预测控制(MPC)_follow轻尘的博客-CSDN博客_mpc代码
Apollo代码学习(六)-模型预测控制(MPC)_follow轻尘的博客-CSDN博客_mpc代码
模型预测控制_模型预测控制(MPC)算法之一MAC算法
引言随着自动驾驶技术以及机器人控制技术的不断发展及逐渐火热,模型预测控制(MPC)算法作为一种先进的控制算法,其应用范围与领域得到了进一步拓展与延伸.目前提出的模型预测控制算法主要有基于非参数模型的 ...
基于模型预测控制(MPC)的悬架系统仿真分析
目录前言 1.悬架系统 2.基于MPC的悬架系统仿真分析 2.1 simulink模型 2.2仿真结果 2.2.1 随机C级路面 2.2.2 正弦路面 2.3 结论 3 总结前言模型预测控制是无 ...
基于扩展卡尔曼滤波EKF和模型预测控制MPC，自动泊车场景建模开发
基于扩展卡尔曼滤波EKF和模型预测控制MPC,自动泊车场景建模开发,文复现. MATLAB 基于扩展卡尔曼滤波EKF和模型预测控制MPC,自动泊车场景建模开发,文复现. MATLAB(工程项目线上支持 ...
无人车系统（十一）：轨迹跟踪模型预测控制(MPC)原理与python实现【40行代码】
前面介绍的PID,pure pursuit方法,Stanley方法都只是利用当前的系统误差来设计控制器.人们对这些控制器的设计过程中都利用了构建模型对无人车未来状态的估计(或者说利用模型估计未来的运动 ...
【控制control】机器人运动控制器----基于模型预测控制MPC方法
系列文章目录提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理文章目录系列文章目录前言一.模型预测控制(MPC)的介绍及构成 1.介绍 2.构成二.模型 ...
【附C++源代码】模型预测控制(MPC)公式推导以及算法实现，Model Predictive control介绍
2022年的第一篇博客,首先祝大家新年快乐! 提示:本篇博客主要集中在对MPC的理解以及应用.这篇博客可以作为你对MPC控制器深入研究的一个开始,起到抛砖引玉,带你快速了解其原理的作用. 这篇博客将介 ...
差分轮移动机器人模型预测控制MPC
模型预测控制(MPC)与PID.纯追踪法相比有更好的路径跟踪效果,在自动驾驶领域有广泛应用.本文将以运动学为基础详细推导差分轮移动机器人模型预测控制(MPC) 运动学模型根据移动机器人的运动学结构可 ...
基于模型预测控制MPC的光伏并网系统设计|太阳能发电|模型预测控制
本课题提出一种基于最大功率点跟踪与有限集模型预测控制结合的光伏并网逆变策略,首先,针对模型预测控制算法在电网模型预测与控制时域中实时性不足等问题,引用快速求解MATMPC工具箱,降低MPC算法的单轮运 ...

lecture09 Convex 模型预测控制（MPC）