神奇的分形艺术（四）：Julia集和Mandelbrot集

考虑函数f(z)=z^2-0.75。固定z0的值后，我们可以通过不断地迭代算出一系列的z值：z1=f(z0), z2=f(z1), z3=f(z2), ...。比如，当z0 = 1时，我们可以依次迭代出：
z1 = f(1.0) = 1.0^2 - 0.75 = 0.25
z2 = f(0.25) = 0.25^2 - 0.75 = -0.6875
z3 = f(-0.6875) = (-0.6875)^2 - 0.75 = -0.2773
z4 = f(-0.2773) = (-0.2773)^2 - 0.75 = -0.6731
z5 = f(-0.6731) = (-0.6731)^2 - 0.75 = -0.2970
...
    可以看出，z值始终在某一范围内，并将最终收敛到某一个值上。
    但当z0=2时，情况就不一样了。几次迭代后我们将立即发现z值最终会趋于无穷大：
z1 = f(2.0) = (2.0)^2 - 0.75 = 3.25
z2 = f(3.25) = (3.25)^2 - 0.75 = 9.8125
z3 = f(9.8125) = (9.8125)^2 - 0.75 = 95.535
z4 = f(95.535) = (95.535)^2 - 0.75 = 9126.2
z5 = f(9126.2) = (9126.2)^2 - 0.75 = 83287819.2
...
    经过计算，我们可以得到如下结论：当z0属于[-1.5, 1.5]时，z值始终不会超出某个范围；而当z0小于-1.5或大于1.5后，z值最终将趋于无穷。
    现在，我们把这个函数扩展到整个复数范围。对于复数z0=x+iy，取不同的x值和y值，函数迭代的结果不一样：对于有些z0，函数值约束在某一范围内；而对于另一些z0，函数值则发散到无穷。由于复数对应平面上的点，因此我们可以用一个平面图形来表示，对于哪些z0函数值最终趋于无穷，对于哪些z0函数值最终不会趋于无穷。我们用深灰色表示不会使函数值趋于无穷的z0；对于其它的z0，我们用不同的颜色来区别不同的发散速度。由于当某个时候|z|>2时，函数值一定发散，因此这里定义发散速度为：使|z|大于2的迭代次数越少，则发散速度越快。这个图形可以编程画出。和上次一样，我用Pascal语言，因为我不会C的图形操作。某个MM要过生日了，我把这个自己编程画的图片送给她^_^

{$ASSERTIONS+}

uses graph;

type complex=record re:real; im:real; end;

operator * (a:complex; b:complex) c:complex; begin c.re := a.re*b.re - a.im*b.im; c.im := a.im*b.re + a.re*b.im; end;

operator + (a:complex; b:complex) c:complex; begin c.re := a.re + b.re; c.im := a.im + b.im; end;

var z,c:complex; gd,gm,i,j,k:integer; begin gd:=D8bit; gm:=m640x480; InitGraph(gd,gm,''); Assert(graphResult=grOk);

c.re:=-0.75; c.im:=0; for i:=-300 to 300 do for j:=-200 to 200 do begin z.re:=i/200; z.im:=j/200; for k:=0 to 200 do begin if sqrt(z.re*z.re + z.im*z.im) >2 then break else z:=(z*z)+c; end; PutPixel(i+300,j+200,k) end;

readln; CloseGraph; end.

代码在Windows XP SP2，FPC 2.0下通过编译，麻烦大家帮忙报告一下程序运行是否正常（上次有人告诉我说我写的绘图程序不能编译）。在我这里，程序运行的结果如下：

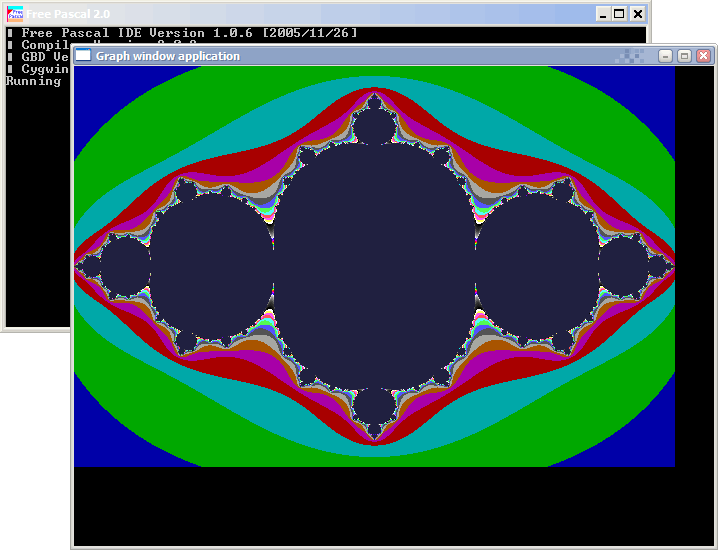
这个美丽的分形图形表现的就是f(z)=z^2-0.75时的Julia集。考虑复数函数f(z)=z^2+c，不同的复数c对应着不同的Julia集。也就是说，每取一个不同的c你都能得到一个不同的Julia集分形图形，并且令人吃惊的是每一个分形图形都是那么美丽。下面的六幅图片是取不同的c值得到的分形图形。你可能不相信这样一个简单的构造法则可以生成这么美丽的图形，这没什么，你可以改变上面程序代码中c变量的值来亲自验证。

c = 0.45, -0.1428

c = 0.285, 0.01

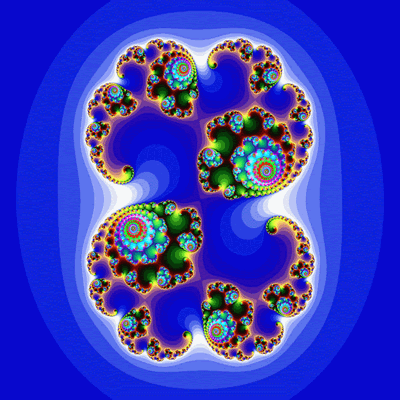
c = 0.285, 0

c = -0.8, 0.156

c = -0.835, -0.2321

c = -0.70176, -0.3842

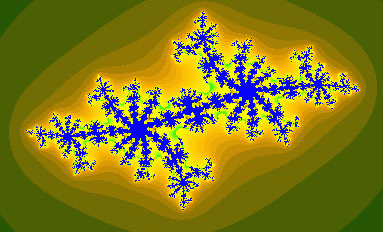
类似地，我们固定z0=0，那么对于不同的复数c，函数的迭代结果也不同。由于复数c对应平面上的点，因此我们可以用一个平面图形来表示，对于某个复数c，函数f(z)=z^2+c从z0=0开始迭代是否会发散到无穷。我们同样用不同颜色来表示不同的发散速度，最后得出的就是Mandelbrot集分形图形：

前面说过，分形图形是可以无限递归下去的，它的复杂度不随尺度减小而消失。Mandelbrot集的神奇之处就在于，你可以对这个分形图形不断放大，不同的尺度下你所看到的景象可能完全不同。放大到一定时候，你可以看到更小规模的Mandelbrot集，这证明Mandelbrot集是自相似的。下面的15幅图演示了Mandelbrot集的一个放大过程，你可以在这个过程中看到不同样式的分形图形。

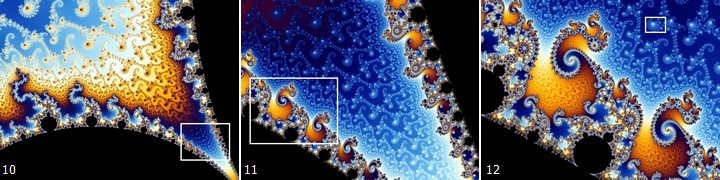
网上可以找到很多小程序实现Mandelbrot集的放大过程。把上面给出的代码改一改，你也可以写出一个这样的程序来。
做人要厚道，转贴请注明出处

神奇的分形艺术（四）：Julia集和Mandelbrot集相关推荐

数学之美之分形——C++及OpenCV实现Julia集和Mandelbrot集绘制
搞了一天,终于全部搞定了,久久惊叹于分形的美而不能自拔-- 先来简单介绍下Julia集和Mandelbrot集:(来自这里) 曼德勃罗特(Mandelbrot)集是人类有史以来做出的最奇异,最瑰丽的几 ...
分形之Julia集和Mandelbrot集及浅谈分形理论的应用
首先要show一把这俩个集合的图片 [img]http://upload.wikimedia.org/wikipedia/commons/a/a4/Mandelbrot_sequence_new.gi ...
python分形几何_使用 Python 绘制分形: Koch 曲线、Julia 集、Mandelbrot 集
目录 1. Koch曲线瑞典数学家Helge von Koch,在1904年发表的"从初等几何构造的一条没有切线的连续曲线"的论文中提出Korch曲线.它的描述如下:指定一条线段 ...
新人如何学分形艺术（第二版）
曾经写过这样一篇文章,以下是链接分形其实很简单[新手如何学分形?] 这是前年网站刚开放不久我尽全力写下来的那时的我同现在的你们一样刚刚学分形懂的也很少但时间如梭一年半过去了这期间我也成长 ...
分形几何python代码_Python, Cython绘制美妙绝伦的Mandelbrot集, 曼德博集分形图案
上世纪60-70年代,美籍数学家曼德博 - Benoit B. Mandelbrot几乎单枪匹马的创立了一个新的数学分支,即分形几何学 - fractal geometry.这个新的数学分支有助于人类 ...
《分形艺术，宇宙之笔，时光之诗！》作者：林晨风达
宇宙之笔,时光之诗! --走进分形艺术作者:林晨风达发表于:中国艺术报向日葵与斐波那契数列图案也许您在哪见过这类图形,它们有着令人惊讶的形状,结构精美,富有哲理,蕴含着神秘的美感.挺吸引眼 ...
另类分形图形赏：2007年分形艺术大赛获奖作品
从2007年分形艺术大赛(Benoit Mandelbrot Fractal Art Contest)中选了几个自己感觉不错的图与大家分享. 图片按以下三个原则来选取: 1. 严格符合分形图形的定义 ...
Python, Cython绘制美妙绝伦的Mandelbrot集, 曼德博集分形图案
上世纪60-70年代,美籍数学家曼德博 - Benoit B. Mandelbrot几乎单枪匹马的创立了一个新的数学分支,即分形几何学 - fractal geometry.这个新的数学分支有助于人类 ...
大自然创作的分形艺术
来源:http://blog.sciencenet.cn/blog-420554-363521.html 数学上的分形 (Fractal) 是指"一个粗糙或零碎的几何形状,可以分成数个部分, ...

神奇的分形艺术（四）：Julia集和Mandelbrot集

神奇的分形艺术（四）：Julia集和Mandelbrot集相关推荐

最新文章

热门文章