一. 简介

离散傅里叶变换（Discrete Fourier Transform, DFT）是数字信号处理最重要的基石之一，也是对信号进行分析和处理时最常用的工具之一。在200多年前法国数学家、物理学家傅里叶提出后来以他名字命名的傅里叶级数之后，用DFT这个工具来分析信号就已经为人们所知。但在很长时间内，这种分析方法并没有引起更多的重视，最主要的原因在于这种方法运算量比较大。

快速傅里叶变换（Fast Fourier Transform, FFT）是1965年由库利（T.W.Cooley）和图基（J.W.Tukey）共同提出的一种快速计算DFT的方法。这种方法充分利用了DFT运算中的对称性和周期性，从而将DFT运算量从N2减少到N*log2N。当N比较小时，FFT优势并不明显。但当N大于32开始，点数越大，FFT对运算量的改善越明显。比如当N为1024时，FFT的运算效率比DFT提高了100倍。

在库利和图基提出的FFT算法中，其基本原理是先将一个N点时域序列的DFT分解为N个1点序列的DFT，然后将这样计算出来的N个1点序列DFT的结果进行组合，得到最初的N点时域序列的DFT值。实际上，这种基本的思想很早就由德国伟大的数学家高斯（1777年4月30日－1855年2月23日）提出过，只是由于当时尚欠东风——计算机还没发明。在20世纪60年代，伴随着计算机的发展和成熟，库利和图基的成果掀起了数字信号处理的革命，因而FFT发明者的桂冠才落在他们头上。

库利和图基的FFT算法的最基本运算为蝶形运算，每个蝶形运算包括两个输入点，因而也称为基-2算法。在这之后，又有一些新的算法，进一步提高了FFT的运算效率，比如基-4算法、分裂基算法等。这些新算法对FFT运算效率的提高一般在50%以内，远远不如FFT对DFT运算的提高幅度。从这个意义上说，FFT算法是里程碑式的。可以说，正是计算机技术的发展和FFT的出现，才使得数字信号处理迎来了一个崭新的时代。

只有周期信号可以通过傅里叶变换分解，随机信号、无规则信号是不能分解的。

二. FFT（Matlab角度分析）

现举例：

假设我们有一个信号（如图一所示），它是一个与时间无关的常数。

它含有

①2V的直流分量（注：信号的直流分量就是信号的平均值），

②频率为50Hz、相位为-30度、幅度为3V的交流信号，

以及一个

③频率为75Hz、相位为90度、幅度为1.5V的交流信号。

用数学表达式就是如下：

式中cos参数的单位为弧度，所以-30度和90度要分别换算成弧度，即各除以180。换算后，是：

拓展：

傅里叶级数的物理意义很明确：把一个周期信号表示为一系列不同频率的复指数信号的线性组合。上公示：

注意，这个公式的最小组成单位是复指数（复数指数）信号，也就是这个：

（

拓展：欧拉公式，对任意实数x，都存在

其中e是自然对数的底数，i是虚数单位，而cos和sin则是余弦、正弦对应的三角函数，参数x则以弧度为单位。

）

我们知道，复指数信号不是实信号，它在现实中是不存在的，因为它带有虚部i。

那如何用复指数信号合成实信号呢？

答案很简单：只要两个复数共轭就好，实部相加，虚部相抵。也就是欧拉公式：

所以我们在用傅里叶级数分析信号的时候，频谱绝对是对称的，用很多对指数相反的复指数信号，就可以合成实信号，也就是说：有k，则必然有-k，否则无法合成实信号。

综上，出现负频率的根本原因就是傅里叶级数（变换）的最小单位是复指数信号，如果用傅里叶级数的另一种形式，把信号表示为一系列正余弦信号的组合，就不存在负频率了。

至于形象的理解，可以看那个帖子的第一页，有图很容易理解。

倍频？
这个解释起来比较简单，采样的过程其实就是周期采样信号乘以模拟信号。

时域的乘积等于频域的卷积，就是下面这个样子：

最终采样之后的信号的频谱就是这样，形成了频谱的延拓，这就是题主说的倍频吧。

例子：

图一

式中cos参数为弧度，所以-30度和90度要分别换算成弧度。我们以256Hz的采样（频）率对这个信号进行采样，总共采样256点。按照我们上面的分析，Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是1Hz，第n个点的频率就是n-1。我们的信号有3个频率：0Hz、50Hz、75Hz，应该分别在第1个点、第51个点、第76个点上出现峰值，其它各点应该接近0。实际情况如何呢？我们来看看FFT的结果的模值如图所示。

图二 FFT结果

从图中我们可以看到，在第1个采样点、第51个采样点、和第76个采样点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看：

1点： 512+0i

2点： -2.6195E-14 - 1.4162E-13i 
3点： -2.8586E-14 - 1.1898E-13i

50点：-6.2076E-13 - 2.1713E-12i
51点：332.55 - 192i
52点：-1.6707E-12 - 1.5241E-12i

75点：-2.2199E-13 -1.0076E-12i
76点：3.4315E-12 + 192i
77点：-3.0263E-14 +7.5609E-13i
 
很明显，1点、51点、76点的值都比较大，它附近的点值都很小，可以认为是0，即在那些频率点上的信号幅度为0。接着，我们来计算各点的幅度值。分别计算这三个点的模值，结果如下：
1点： 512
51点：384
76点：192

按照公式，可以计算出：

直流分量为：512/N=512/256=2；

50Hz信号的幅度为：384/(N/2)=384/(256/2)=3；

75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。

可见，从频谱分析出来的幅度是正确的。

然后再来计算相位信息。直流信号没有相位可言，不用管它。先计算50Hz信号的相位，atan2(-192, 332.55)=-0.5236,结果是弧度，换算为角度就是180*-0.5236)/pi=-30.0001。再计算75Hz信号的相位，atan2(192, 3.4315E-12)=1.5708弧度，换算成角度就是180*1.5708/pi=90.0002。可见，相位也是对的。根据FFT结果以及上面的分析计算，我们就可以写出信号的表达式了，它就是我们开始提供的信号。

总结：假设采样频率为Fs，采样点数为N，做FFT之后，某一点n（n从1开始）表示的频率为：Fn=(n-1)*Fs/N；该点的模值除以N/2就是对应该频率下的信号的幅度（对于直流信号是除以N）；该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值，范围从-pi到pi。要精确到xHz，则需要采样长度为1/x秒的信号，并做FFT。要提高频率分辨率，就需要增加采样点数，这在一些实际的应用中是不现实的，需要在较短的时间内完成分析。解决这个问题的方法有频率细分法，比较简单的方法是采样比较短时间的信号，然后在后面补充一定数量的0，使其长度达到需要的点数，再做FFT，这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。

[附录：本测试数据使用的matlab程序]

close all;       % 先关闭所有图片
Adc=2;           % 直流分量幅度
A1=3;            % 频率F1信号的幅度
A2=1.5;          % 频率F2信号的幅度
F1=50;           % 信号1频率(Hz)
F2=75;           % 信号2频率(Hz)
Fs=256;          % 采样频率(Hz)
P1=-30;          % 信号1相位(度)
P2=90;           % 信号2相位(度)
N=256;           % 采样点数
t=[0:1/Fs:N/Fs]; % 采样时刻% 信号
S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);
% 显示原始信号
plot(S);
title('原始信号');figure;
Y = fft(S,N);                % 做FFT变换
Ayy = (abs(Y));              % 取模
plot(Ayy(1:N));              % 显示原始的FFT模值结果
title('FFT 模值');figure;
Ayy=Ayy/(N/2);               % 换算成实际的幅度
Ayy(1)=Ayy(1)/2;
F=([1:N]-1)*Fs/N;            % 换算成实际的频率值
plot(F(1:N/2),Ayy(1:N/2));   % 显示换算后的FFT模值结果
title('幅度-频率曲线图');figure;
Pyy=[1:N/2];
for i=[1:N/2]
Pyy(i)=phase(Y(i));          % 计算相位
Pyy(i)=Pyy(i)*180/pi;        % 换算为角度
end;
plot(F(1:N/2),Pyy(1:N/2));   % 显示相位图
title('相位-频率曲线图');

Matlab的实验结果如下：

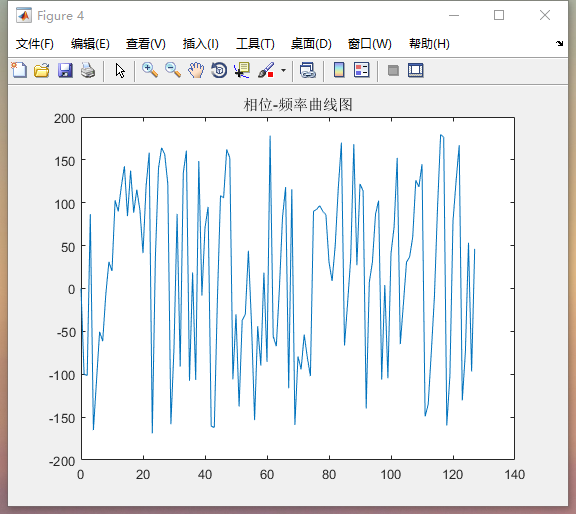
看完这个你就明白谐波分析了。

三. FFT（数学角度分析）

FFT的具体计算过程可以通过蝶形图可视化：

第一次分解：

第二次分解：

第三次分解：

FFT与DFT的性能比较：

除了运算效率的大幅度提高外，FFT还大大降低了DFT运算带来的累计量化误差，这点常为人们所忽略。