骨牌覆盖问题总结!hihoCoder/ NYOJ-1273宣传墙1151
本想着做一下第九届河南省省赛题,结果被这个类似骨牌覆盖的题卡住了,队友然我去hihoCoder上老老实实把骨牌覆盖一、二、三做完,这题就没什么问题了。虽然很不情愿,但还是去见识了一下。
#1143 : 骨牌覆盖问题·一
提示:骨牌覆盖
我们考虑在已经放置了部分骨牌(灰色)的情况下,下一步可以如何放置新的骨牌(蓝色):
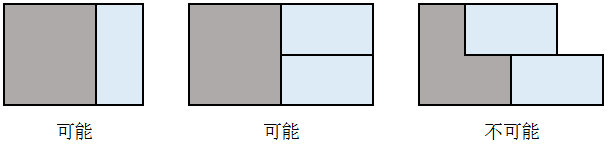
最右边的一种情况是不可能发生的,否则会始终多一个格子没有办法放置骨牌。或者说灰色部分的格子数为奇数,不可能通过1x2个骨牌放置出来。
那么通过对上面的观察,我们可以发现:
在任何一个放置方案最后,一定满足前面两种情况。而灰色的部分又正好对应了长度为N-1和N-2时的放置方案。由此,我们可以得到递推公式:
f[n] = f[n-1] + f[n-2];
这个公式是不是看上去很眼熟?没错,这正是我们的费波拉契数列。
f[0]=1,f[1]=1,f[2]=2,...
由于本题N很大,所以利用矩阵快速幂来优化。
提示:如何快速计算结果
当N很小的时候,我们直接通过递推公式便可以计算。当N很大的时候,只要我们的电脑足够好,我们仍然可以直接通过递推公式来计算。
但是我们学算法的,总是这样直接枚举不是显得很Low么,所以我们要用一个好的算法来加速(装X)。
事实上,对于这种线性递推式,我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列,我们希望找到一个2x2的矩阵M,使得(a, b) x M = (b, a+b),其中(a, b)和(b, a+b)都是1x2的矩阵。
显然,只需要取M = [0, 1; 1, 1]就可以了:
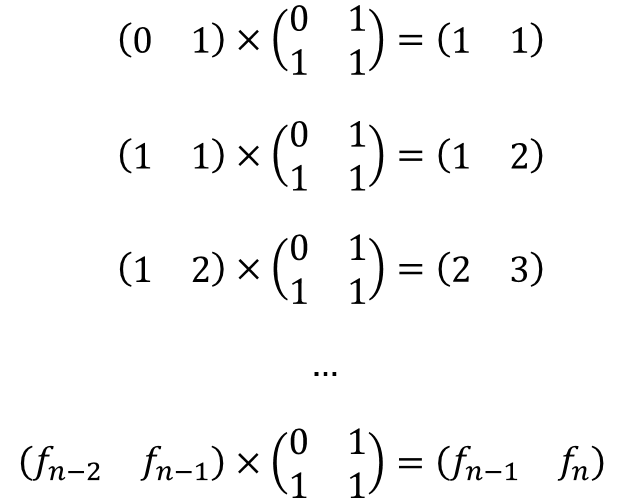
进一步得到:

那么接下来的问题是,能不能快速的计算出M^n?我们先来分析一下幂运算。由于乘法是满足结合律的,所以我们有:
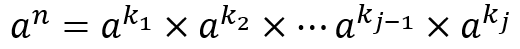
不妨将k[1]..k[j]划分的更好一点?
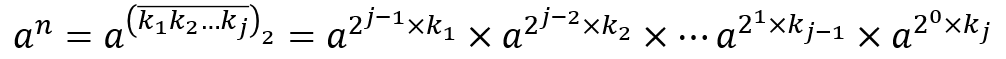
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质:
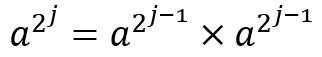
结合这两者我们可以得到一个算法:
1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)},因为该数列满足递推公式,时间复杂度为O(logN)
2. 将指数n二进制化,再利用公式将对应的a^j相乘计算出a^n,时间复杂度仍然为O(logN)
则总的时间复杂度为O(logN)
这种算法因为能够在很短时间内求出幂,我们称之为“快速幂”算法。
#1151 : 骨牌覆盖问题·二
对于3xN的棋盘,使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢?很显然N为奇数是不可能的。
提示:3xN骨牌覆盖
在2xN的骨牌覆盖问题中,我们有递推式子 (0,1)xM^n=(f[n-1],f[n])。
我们考虑能否在3xN的情况下找到同样的式子。
但在实际的推导过程可以发现,对于3xN的覆盖,对应的f数值公式比2xN复杂太多。我们需要换个角度来思考推导公式。
在我们放置骨牌的过程中,一定是放好一行之后再放置下一行。根据摆放的方式,可能会产生很多种不同的形状,而这些形状之间是否具有某些递推关系呢?
如果他们存在一定的递推关系,则我们可以根据第i行的方案数来推导第i+1行的方案数。这样一行一行推导,直到第N行时不就得到了我们要求的方案数了么?
那么来研究一下是否存在这样的推导公式吧
假设我们已经放好了一些骨牌,对于当前最后一列(第i列)骨牌,可能有8种情况:
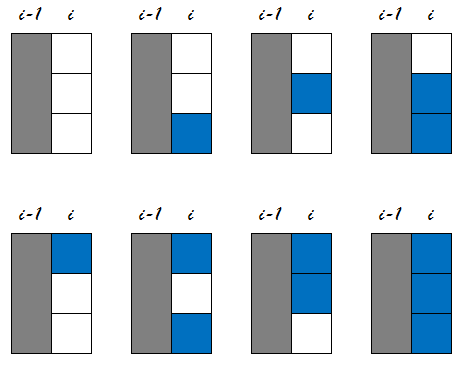
对于上面这8种状态,我们用数字来标记它们。以有放置骨牌的格子为1,未放置为0,转化为2进制数
以最下面一行作为1,则有:
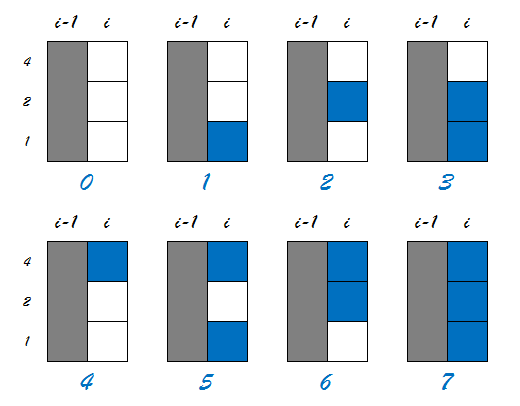
接下来考虑如何放置骨牌,我们先将棋盘旋转一下。假设我们正在放置第i行的骨牌,那么会有下面3种方式:
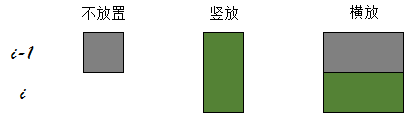
灰色表示已经有的骨牌,绿色表示新放置的骨牌。
每一种放置方法解释如下,假设当第i行的状态为x,第i-1行的状态为y:
第i行不放置,则前一行必须有放置的骨牌。x对应二进制位为0,y对应二进制位为1。第i行竖放骨牌,则前一行必须为空。x对应二进制位为1,y对应二进制位为0。第i行横向骨牌,则前一行必须两个位置均有骨牌,否则会产生空位。x对应二进制位为1,y对应二进制位为1。
举个例子:
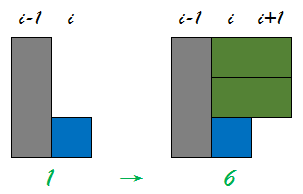
对于第i行状态1,我们在第i+1行竖放两块骨牌之后便能到达状态6。
但是在这之中需要注意会出现下面这种情况:
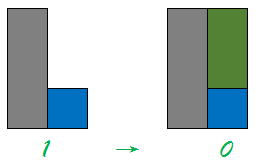
这种情况看似是从状态1变成了状态0,其实是不对的。它不满足我们约定的放置方法,本质是第i行的状态1变成了第i行的状态7,而实际上我们应该放置的是第i+1行。
所以在枚举递推关系的时候一定要注意。
通过枚举8种状态到8种状态的转移,我们可以得到一个8x8的矩阵M(空白的地方均为0):
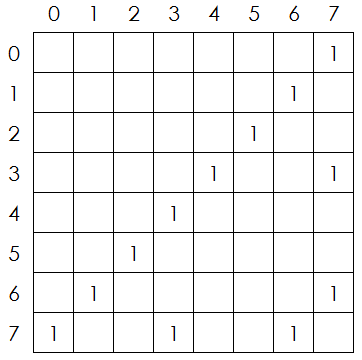
m[i][j]表示从状态i变成状态j的方案数。
现在我们有了M矩阵,接下来考虑边界情况。
在2xN的骨牌覆盖中,有(0, 1)作为初始向量A,那么在3xN中初始向量A是如何呢?
让我们先想想A向量所代表的含义。M矩阵表示状态到状态的转移,则A向量所表示的应该就是第0行各状态的方案数。
同理,对于A * M^n所求出的结果则应该表示为第n行各种状态的方案数。
那么A向量应该是多少呢?很显然,第0行在我们递推的过程中必须看作状态7才合理。故A向量表示为:
{0, 0, 0, 0, 0, 0, 0, 1}
而对于我们寻求的答案,自然也是第n行放置为状态7的方案数了。
struct martix
{ll a[9][9];
};
int n;
martix mul(martix A,martix B)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<8; i++)for(int j=0; j<8; j++)for(int k=0; k<8; k++)res.a[i][j]=(res.a[i][j]+A.a[i][k]*B.a[k][j])%MOD;return res;
}
martix fast(martix tmp,int num)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<8; i++) res.a[i][i]=1;while(num){if(num&1) res=mul(res,tmp);tmp=mul(tmp,tmp);num>>=1;}return res;
}
void solve()
{martix res,ans;memset(res.a,0,sizeof(res.a));memset(ans.a,0,sizeof(res.a));for(int i=0; i<8; i++) res.a[7-i][i]=1;res.a[3][7]=res.a[6][7]=res.a[7][3]=res.a[7][6]=1;ans.a[0][7]=1;res=fast(res,n);ans=mul(ans,res);printf("%lld\n",ans.a[0][7]);
}
int main()
{while(~scanf("%d",&n)){solve();}return 0;
}#1162 : 骨牌覆盖问题·三
对于给定的K和N,我们需要去求KxN棋盘的覆盖方案数。棋盘宽度为k,长度为N。2≤K≤7,1≤N≤100,000,000
提示:KxN骨牌覆盖
在2xN的骨牌问题中,我们有答案的递推序列。f[n] = f[n-1]+f[n-2]。
事实上在处理3xN的问题中,也有部分选手推导出了答案的递推序列。
那么对于4xN,5xN,是否也存在答案的递推序列呢?有兴趣的选手不妨尝试推导一下。
在上一期,也就是3xN问题中,我们介绍了根据状态来递推的方法。这种方法显然是通用性最好的,可以用来解决任何K值的覆盖。
对于任意一个K值,我们每一行拥有的状态数量为2^K种。
在K=3时,我们是通过手动来枚举的8种状态之间的递推关系。
当K=4或者更大的时候,再通过手动枚举就显得不那么科学了,此时我们需要考虑如何用程序生成我们所需要的状态转移矩阵。
让我们再回头看看我们上一期提示里面放置骨牌的约定:
假设我们正在放置第i行的骨牌,那么会有下面3种方式:
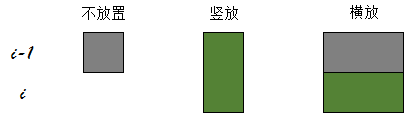
灰色表示已经有的骨牌,绿色表示新放置的骨牌。
每一种放置方法解释如下,假设当第i行的状态为x,第i-1行的状态为y:
第i行不放置,则前一行必须有放置的骨牌。x对应二进制位为0,y对应二进制位为1。第i行竖放骨牌,则前一行必须为空。x对应二进制位为1,y对应二进制位为0。第i行横向骨牌,则前一行必须两个位置均有骨牌,否则会产生空位。x对应二进制位为1,y对应二进制位为1。
既然有对应的二进制描述,那么上面三种方法就可以用程序语言解释为:第i行不放置:new_x = x << 1, new_y = (y << 1) + 1; 列数+1第i行竖放骨牌:new_x = (x << 1) + 1, new_y = y << 1; 列数+1第i行横向骨牌:new x = (x << 2) + 3, new_y = (y << 2) + 3; 列数+2
通过迭代去枚举3种放置方法,当总的列数等于K时,此时的x便可由y转移过来。那么我们可以得到枚举放置的伪代码:
DFS(x, y, col):If col == Kd[y][x] = 1Return ;EndDFS(x << 1, (y << 1) + 1, col + 1);DFS((x << 1) + 1, y << 1, col + 1);If col + 2 <= KDFS( (x << 2) + 3, (y << 2) + 3, col + 2 )End
当我们得到对应的矩阵之后,剩下需要做的也就和上一期相同了。
在某些题目中有可能会出现,N很小,K很大的情况。比如N=20,K=14这样的情况。
考虑到N很小,我们可以不使用矩阵乘法,而直接采用f[i-1]到f[i]行的递推。时间复杂度也就转化为2^(2k)*N。
但是状态数量为2^14,也就是16384种。若采用转移矩阵,肯定是无法储存的。而实际情况是在转移矩阵中1的数量并不多,所以我们可以考虑存储为(y,x)这样的二元组。在转移过程中只枚举合法的转移即可。
若K再更大一点,比如K=20,产生的状态有可能连开数组存储都很吃力。这个时候我们也可以考虑在计算每一行时,直接通过dfs来进行转移,不储存转移关系。用时间来换取空间。
struct martix
{ll a[150][150];
};
int k,n;
martix mul(martix A,martix B)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<130; i++)for(int j=0; j<130; j++)for(int k=0; k<130; k++)res.a[i][j]=(res.a[i][j]+A.a[i][k]*B.a[k][j])%MOD;return res;
}
martix fast(martix tmp,int num)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<130; i++) res.a[i][i]=1;while(num){if(num&1) res=mul(res,tmp);tmp=mul(tmp,tmp);num>>=1;}return res;
}
void dfs(int x,int y,int num,martix &res)
{if(num==k){res.a[y][x]=1;return ;}dfs(x<<1,(y<<1)+1,num+1,res);//加减比左移优先级高dfs((x<<1)+1,y<<1,num+1,res);if(num+2<=k) dfs((x<<2)+3,(y<<2)+3,num+2,res);
}
void solve()
{martix res;memset(res.a,0,sizeof(res.a));dfs(0,0,0,res);res=fast(res,n);printf("%lld\n",res.a[(1<<k)-1][(1<<k)-1]);
}
int main()
{while(~scanf("%d%d",&k,&n)){solve();}return 0;
}
有了上面的基础,如何来解决第九届河南省省赛的那道类似骨牌覆盖问题呢。
基于数据较小,队友是强行dp过去的,但对于我这种dp弱渣还是老老实实用矩阵快速幂来的更快些。
宣传墙
一条4*N道路被分为左右两个矩形,然后用1*2的骨牌去覆盖,求各有多少种方法。很明显左边矩形是4*(M-1),右边矩形是4*(N-M-K+1)。其实根据骨牌覆盖三我们很容易得到k为4的系数矩阵。只需在上面的代码将k改为4即可。
struct martix
{ll a[150][150];
};
int k,n,m,kk;
martix mul(martix A,martix B)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<16; i++)for(int j=0; j<16; j++)for(int k=0; k<16; k++)res.a[i][j]=(res.a[i][j]+A.a[i][k]*B.a[k][j])%MOD;return res;
}
martix fast(martix tmp,int num)
{martix res;memset(res.a,0,sizeof(res.a));for(int i=0; i<16; i++) res.a[i][i]=1;while(num){if(num&1) res=mul(res,tmp);tmp=mul(tmp,tmp);num>>=1;}return res;
}
void dfs(int x,int y,int num,martix &res,martix &ans)
{if(num==k){res.a[y][x]=1;ans.a[y][x]=1;return ;}dfs(x<<1,(y<<1)+1,num+1,res,ans);//加减比左移优先级高dfs((x<<1)+1,y<<1,num+1,res,ans);if(num+2<=k) dfs((x<<2)+3,(y<<2)+3,num+2,res,ans);
}
void solve()
{k=4;martix res,ans;memset(res.a,0,sizeof(res.a));memset(ans.a,0,sizeof(ans.a));dfs(0,0,0,res,ans);res=fast(res,m-1);int ans1=res.a[15][15];ans=fast(ans,n-m-kk+1);int ans2=ans.a[15][15];printf("%d %d\n",ans1,ans2);
}
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d%d%d",&n,&m,&kk);solve();}return 0;
}本想着和队友探讨一下如果单位矩阵不是1*2的,而是2*3或者其它的怎么做,然而队友推翻了我这种想法,也许出题人不会这样出题。有兴趣可以一(不)起(惜)探(赐)讨(教)
转载于:https://www.cnblogs.com/nyist-TC-LYQ/p/7208063.html
骨牌覆盖问题总结!hihoCoder/ NYOJ-1273宣传墙1151相关推荐
- nyoj 1273 宣传墙
题目链接:点击打开链接 题意:给你一个4*n的矩阵,你有1*2的砖头若干,让你进行铺砖,在中间m ---- m+k的部分你不用铺.问左边和右边的方法数各位多少. 题解:因为数据偏大,需要滚动数组来优化 ...
- hihoCoder #1143 : 骨牌覆盖问题·一
#1143 : 骨牌覆盖问题·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具.今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形棋盘, ...
- 编程之美 --1 : 骨牌覆盖问题·一
题目1 : 骨牌覆盖问题·一 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 骨牌,一种古老的玩具.今天我们要研究的是骨牌的覆盖问题: 我们有一个2xN的长条形棋盘,然后 ...
- 随便玩玩系列之一:SPOJ-RNG+51nod 算法马拉松17F+51nod 1034 骨牌覆盖v3
先说说前面的SPOJ-RNG吧,题意就是给n个数,x1,x2,...,xn 每次可以生成[-x1,x1]范围的浮点数,把n次这种操作生成的数之和加起来,为s,求s在[A,B]内的概率 连续形的概率 假 ...
- 骨牌覆盖问题 KxM
前面我们说了一些简单的骨牌覆盖问题,有了上面的经验,我们可以尝试解决K*M的 思路和上一篇文章所提到的3*N的 很类似: 依然是矩阵快速幂.我们需要把一个小的边固定下来作为的已知边,然后进行矩阵快速幂 ...
- 51Nod-1031 骨牌覆盖【递推】
1031 骨牌覆盖 基准时间限制:1 秒 空间限制:131072 KB 分值: 10 难度:2级算法题 在2*N的一个长方形方格中,用一个1*2的骨牌排满方格. 问有多少种不同的排列方法. 例如:2 ...
- nyoj-1273 宣传墙
题目1273 题目信息 运行结果 本题排行 讨论区 宣传墙 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描述 ALPHA 小镇风景美丽,道路整齐,干净,到此旅游的游客特别多 ...
- nyoj1273 河南省第九届省赛_宣传墙、状压DP+矩阵幂加速
宣传墙 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描述 ALPHA 小镇风景美丽,道路整齐,干净,到此旅游的游客特别多.CBA 镇长准备在一条道路南 面 4*N 的墙上做 ...
- NYOJ_1273_宣传墙
/* 宣传墙 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描述 ALPHA 小镇风景美丽,道路整齐,干净,到此旅游的游客特别多.CBA 镇长准备在一条道路南 面 4*N 的 ...
最新文章
- hue 添加jar_在hue下配置jdbc驱动
- windows2003配置
- 大话 JavaScript 动画
- 实现销售榜单下载功能
- RHEL 8 - 用podman/buildah/skopeo构建systemd级别运行容器
- Spring AOP配置
- js 字符串编码与解码
- [转] 面试必问的16个经典问题的回答思路
- C# action 返回值_C#知识点讲解之C#delegate、event、Action、EventHandler的使用和区别
- python ai 源码_2018年撩课学院-Python+人工智能/JavaEE/Web全栈/全学科下载_Python教程...
- 耿楠《LaTeX 中文教程》随堂学习记录
- CPK的概念及其算法
- 从零开始实现一个颜色选择器(原生JavaScript实现)
- xmapp启动之路径错误
- 开发公链社群币种钱包系统软件
- oss 视频 转码_oss视频转码----比阿里云文档更详细
- 有没有测试牙齿需不需要修正的软件,测一测,你的牙齿需要矫正吗?
- VMware安装CentOS8简单教程
- 【excel】定位列内差异/定位行内容差异单元格
- 查看树莓派3 WiFi连接速度
