监督学习 | 线性回归 之正则线性模型原理及Sklearn实现
文章目录
- 1. 正则线性模型
- 1.1 Ridge Regression（L2）
- 1.1.1 Sklearn 实现
- 1.1.2 Ridge + SDG
- 1.1.2.1 Sklearn 实现
- 1.2 Lasso Regression（L1）
- 1.2.1 Sklearn 实现
- 1.2.2 Lasso + SGD
- 1.2.2.1 Sklearn 实现
- 1.3 Elastic Net（L1&L2）
- 1.3.1 Sklearn 实现
- 1.4 正则线性模型选择
- 参考资料
相关文章：
机器学习 | 目录
机器学习 | 回归评估指标
机器学习 | 梯度下降原理及Python实现
监督学习 | 线性回归 之多元线性回归原理及Sklearn实现
监督学习 | 非线性回归 之多项式回归原理及Sklearn实现
监督学习 | 线性分类 之Logistic回归原理及Sklearn实现
1. 正则线性模型
在介绍正则线性模型（Regularized Linear Models）前，我们先来看一下一个例子，假设对于以下数据，我们分别使用多元线性回归和多项式回归进行拟合分类如下：
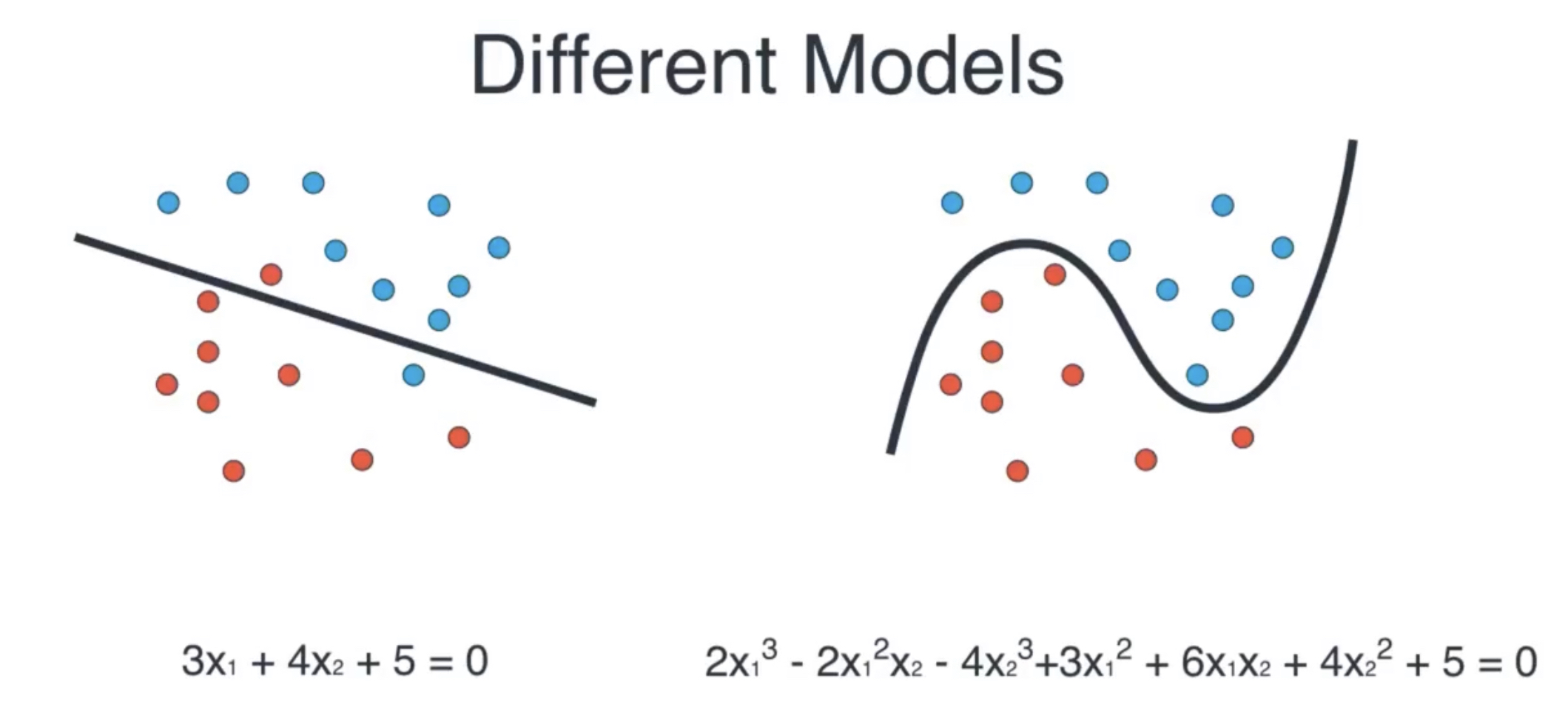图1 不同模型对数据的拟合
可以看到此时线性模型的错误分类点数为2，而多项式回归模型的误差为0，因此此时计算机将会选择第二个模型。但是这个模型有一个缺点，那就是过拟合了，但如何让计算机避免过拟合呢，一个常见的方法就是对模型正则化，它拥有的自由度越低，就越不容易过度拟合。比如，将多项式模型正则化的简单方法就是降低多项式的阶数。
对线性模型来说，正则化通常通过约束模型的权重来实现。如刚才的例子，如果我们为模型的成本函数添加一个模型复杂度的话，就可以在挑选模型的时候考虑到模型的复杂度。
按照对模型复杂度的惩罚不同，我们有三种方法：岭回归、套索回归和弹性网络，分别对应三种正则化策略：L2 正则化、L1 正则化和 L1&L2 正则化。
p-范数：如果 X=[x1,x2,..,xn]X=[x_1,x_2,..,x_n]X=[x1,x2,..,xn] 那么向量 x 的 p-范数就是：∣∣x∣∣p=(∣x1∣p+∣x2∣p+⋯+∣xn∣p)1p||x||_p=(|x_1|^p+|x_2|^p+\cdots+|x_n|^p)^{\frac{1}{p}}∣∣x∣∣p=(∣x1∣p+∣x2∣p+⋯+∣xn∣p)p1 ，用得最多的还是 L1,L2L_1,L_2L1,L2 范数：
L1L_1L1 范数：∣∣x∣∣1=(∣x1∣+∣x2∣+⋯+∣xn∣)||x||_1=(|x_1|+|x_2|+\cdots+|x_n|)∣∣x∣∣1=(∣x1∣+∣x2∣+⋯+∣xn∣) ，即绝对值之和
L2L_2L2 范数：∣∣x∣∣2=(∣x1∣2+∣x2∣2+⋯+∣xn∣2)12||x||_2=(|x_1|^2+|x_2|^2+\cdots+|x_n|^2)^{\frac{1}{2}}∣∣x∣∣2=(∣x1∣2+∣x2∣2+⋯+∣xn∣2)21 ，即通常意义上的模
1.1 Ridge Regression（L2）
岭回归（Ridge Regression，也叫作吉洪诺夫正则化）是线性回归的正则化版：在成本函数中添加一个等于 α∑i=1nθi2\alpha\sum_{i=1}^n\theta_i^2α∑i=1nθi2 的正则项。这使得学习中的算法不仅需要拟合数据，同时还要让模型权重保持最小。
岭回归模型成本函数：
(1)J(θ)=MSE(θ)+α12∑i=1nθi2J(\theta)=MSE(\theta)+\alpha\frac{1}{2}\sum_{i=1}^n\theta_i^2 \tag{1}J(θ)=MSE(θ)+α21i=1∑nθi2(1)
注意，正则项只能在训练的时候添加到成本函数中，一旦训练完成，就需要使用未经正则化的性能指标来评估模型性能。
超参数 α\alphaα 控制的是对模型进行正则化的程度，如果 α=0\alpha=0α=0 ，则岭回归就是线性模型。如果 α\alphaα 非常大，那么所有的权重都非常接近于零，结果是一条穿过数据平均值的水平线。
注意，这里偏置项 θ0\theta_0θ0 没有正则化。如果我们将 www 定义为特征权重的向量（θ1\theta_1θ1 到 θn\theta_nθn），那么正则项即正与 12(∣∣w∣∣2)2\frac{1}{2}(||w||_2)^221(∣∣w∣∣2)2，其中 ∣∣w∣∣2||w||_2∣∣w∣∣2 为权重向量的 L2L_2L2 范数。而对于梯度下降，只需要在 MSEMSEMSE 梯度向量上添加 αw\alpha wαw 即可。
在执行岭回归之前，必须对数据进行缩放（例如使用 StandardScaler），因为它对输入特征的大小非常敏感。大多数正则化模型都是如此。
与线性回归一样，我们也可以在计算闭式方程或者执行梯度下降时，执行岭回归。
闭式解的岭回归：
(2)θ^=(XT⋅X+αA)−1⋅XT⋅y\hat{\theta}=(X^T\cdot X+\alpha A)^{-1}\cdot X^T \cdot y \tag{2}θ^=(XT⋅X+αA)−1⋅XT⋅y(2)
其中 AAA 是一个 n×nn \times nn×n 的单位矩阵，除了左上单元格为0，其他与偏置项对应。
下面是使用不同 α\alphaα 值对某个线性数据进行训练的几种岭回归模型，左边直接对线性模型使用岭回归（即对多元线性模型的成本函数添加模型复杂度），导致预测是线性的。而右边，首先使用 PolynomialFeatures(degree=10) 对数据进行扩展（多项式回归），然后用 StandardScaler() 进行缩放，最后将岭回归模型用于结果特征：
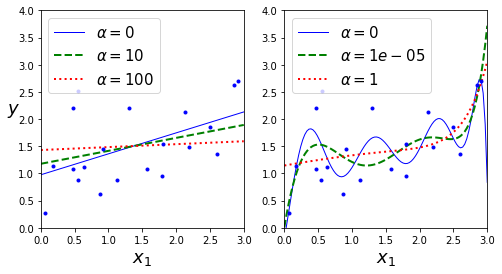图2 不同 alpha 下的 岭回归 与 多项式岭回归
α\alphaα 使得预测更加平坦，这降低了模型的方差，但是也提升了偏差。
代码如下：
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
import matplotlib.pyplot as pltnp.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)def plot_model(model_class, polynomial, alphas, **model_kargs):for alpha, style in zip(alphas, ("b-", "g--", "r:")):# 岭回归如果alpha为0，就变成了线性回归model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression() # 多项式岭回归if polynomial:model = Pipeline([("poly_features", PolynomialFeatures(degree=10, include_bias=False)),("std_scaler", StandardScaler()),("regul_reg", model),])model.fit(X, y)y_new_regul = model.predict(X_new)lw = 2 if alpha > 0 else 1plt.plot(X_new, y_new_regul, style, linewidth=lw, label=r"$\alpha = {}$".format(alpha))plt.plot(X, y, "b.", linewidth=3)plt.legend(loc="upper left", fontsize=15)plt.xlabel("$x_1$", fontsize=18)plt.axis([0, 3, 0, 4])plt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Ridge, polynomial=True, alphas=(0, 10**-5, 1), random_state=42)plt.show()
1.1.1 Sklearn 实现
sklearn.linear_model.Ridge:
from sklearn.linear_model import Ridgeridge_reg = Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)ridge_reg.fit(X, y)
ridge_reg.predict([[X_pred]])
from sklearn.linear_model import Ridgenp.random.seed(42)
m = 20
X = 3 * np.random.rand(m, 1)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5ridge_reg = Ridge(alpha=1, solver="cholesky", random_state=42)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])
array([[1.55071465]])
ridge_reg.intercept_, ridge_reg.coef_
(array([1.00650911]), array([[0.36280369]]))
与原回归模型 y=1+0.5×X+εy = 1 + 0.5 \times X + \varepsilony=1+0.5×X+ε 很接近。
1.1.2 Ridge + SDG
利用随机梯度下降来求解岭回归。
1.1.2.1 Sklearn 实现
from sklearn.linear_model import SGDRegressorridge_sgd_reg = SGDRegressor(max_iter=50, tol=-np.infty, penalty="l2", random_state=42)
ridge_sgd_reg.fit(X, y.ravel())
ridge_sgd_reg.predict([[1.5]])
array([1.49905184])
ridge_sgd_reg.intercept_, ridge_sgd_reg.coef_
(array([0.63725132]), array([0.57453367]))
1.2 Lasso Regression（L1）
线性回归的另一种正则化，叫作最小绝对收缩和选择算子回归（Least Absolute Shrinkage and Selection Operator Regression，简称Lasso 回归，或套索回归）。与岭回归一样，它也是像成本函数添加一个正则项，但是它增加的是权重向量的 L1L_1L1 范数，而不是 L2L_2L2 范数的平方的一半。
Lasso 回归成本函数：
(3)J(θ)=MSE(θ)+α∑i=1n∣θi∣J(\theta)=MSE(\theta)+\alpha\sum_{i=1}^n|\theta_i| \tag{3}J(θ)=MSE(θ)+αi=1∑n∣θi∣(3)
图 3 显示内容与图 2 相同，但是岭回归模型换成了 Lasso 回归模型，同时 α\alphaα 值较小。
Lasso 回归的一个重要特点是它倾向于完全消除掉最不重要特征的权重（也就是将它们设置为零）。例如，在图 3 中右图中的虚线（α=10−7\alpha=10^{-7}α=10−7）看起来像是二次的，快要接近于线性；因为所有高阶多项式的特征权重的等于零。换句话说，Lasso 会回会自动执行特征选择并输出一个系数模型（即只有很少的特征有非零权重）。
图3 不同 alpha 下的 Lasso 回归 与 多项式 Lasso 回归
代码如下：
from sklearn.linear_model import Lassoplt.figure(figsize=(8,4))
plt.subplot(121)
plot_model(Lasso, polynomial=False, alphas=(0, 0.1, 1), random_state=42)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.subplot(122)
plot_model(Lasso, polynomial=True, alphas=(0, 10**-7, 1), tol=1, random_state=42)plt.show()
[外链图片转存失败(img-rtHntb2V-1566830619833)(output_18_0.png)]
1.2.1 Sklearn 实现
sklearn.linear_model.Lasso:
from sklearn.linear_model import Lassolasso_reg = Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')
lasso_reg.fit(X, y)
lasso_reg.predict([[X_pred]])
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])
array([1.53788174])
lasso_reg.intercept_, lasso_reg.coef_
(array([1.14537356]), array([0.26167212]))
1.2.2 Lasso + SGD
利用随机梯度下降来求解 Lasso 回归，当 θi=0(i=1,2,⋯ ,n)\theta_i=0(i=1,2,\cdots,n)θi=0(i=1,2,⋯,n) ，Lasso 成本函数是不可微的。但是，当任意 θi=0\theta_i=0θi=0 时，可以使用次梯度向量 ggg 作为替代，依旧可以让梯度下降正常运转。
LassoLassoLasso 回归次梯度向量：
(4)g(θ,J)=∇θMSE(θ)+α(sign(θ1)sign(θ2)⋮sign(θn))当sign(θ1)={−1(θi<0)0(θi=0)+1(θi>0)g(\theta, J)=\nabla_{\theta} \operatorname{MSE}(\theta)+\alpha\left(\begin{array}{c}{\operatorname{sign}\left(\theta_{1}\right)} \\ {\operatorname{sign}\left(\theta_{2}\right)} \\ {\vdots} \\ {\operatorname{sign}\left(\theta_{n}\right)}\end{array}\right) 当sign(\theta_1)=\left\{ \begin{aligned} -1 \quad (\theta_i<0) \\ 0 \quad (\theta_i=0) \\ +1 \quad (\theta_i>0) \\ \end{aligned} \right.\tag{4} g(θ,J)=∇θMSE(θ)+α⎝⎜⎜⎜⎛sign(θ1)sign(θ2)⋮sign(θn)⎠⎟⎟⎟⎞当sign(θ1)=⎩⎪⎨⎪⎧−1(θi<0)0(θi=0)+1(θi>0)(4)
1.2.2.1 Sklearn 实现
from sklearn.linear_model import SGDRegressorlasso_sgd_reg = SGDRegressor(max_iter=50, tol=-np.infty, penalty="l1", random_state=42)
lasso_sgd_reg.fit(X, y.ravel())
lasso_sgd_reg.predict([[1.5]])
array([1.49903849])
lasso_sgd_reg.intercept_, lasso_sgd_reg.coef_
(array([0.63727982]), array([0.57450578]))
1.3 Elastic Net（L1&L2）
弹性网络是岭回归与 Lasso 回归之间的中间地带。其正则项就是岭回归和 Lasso 回归的正则项的混合混合比例通过 rrr (L1_ratio)来控制。当 r=0r=0r=0 时，弹性网络即等同于岭回归，而当 r=1r=1r=1 时，即相当于 Lasso 回归。
弹性网络成本函数：
(5)J(θ)=MSE(θ)+rα∑i=1n∣θi∣+1−r2α∑i=1nθinJ(\theta)=MSE(\theta)+r\alpha \sum_{i=1}^n|\theta_i|+\frac{1-r}{2}\alpha\sum_{i=1}^n \theta_i^n \tag{5}J(θ)=MSE(θ)+rαi=1∑n∣θi∣+21−rαi=1∑nθin(5)
1.3.1 Sklearn 实现
sklearn.linear_model.ElasticNet:
from sklearn.linear_model import ElasticNetelastic_net = ElasticNet(alpha=1.0, l1_ratio=0.5, fit_intercept=True, normalize=False, precompute=False, max_iter=1000, copy_X=True, tol=0.0001, warm_start=False, positive=False, random_state=None, selection='cyclic')[source]elastic_net.fit(X, y)
elastic_net.predict([[X_pred]])
from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5, random_state=42)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])
array([1.54333232])
elastic_net.intercept_, elastic_net.coef_
(array([1.08639303]), array([0.30462619]))
1.4 正则线性模型选择
应该如何选择线性、岭回归、Lasso 回归和弹性网络呢？通常来说，有正则化——哪怕是很小，总是比没有更可取一些。所以大多数情况下，应该避免使用纯线性回归。
岭回归是个不错的默认选择，但是如果觉得实际用到的特征只有少数几个，那就应该更倾向于 Lasso 回归或是弹性网络，因为它们会将无用特征的权重降为零。
一般而言，弹性网络优于 Lasso 回归，因为当特征数量超过训练实例数量，又或者是几个特征强相关时，Lasso 回归的表现可能非常不稳定。[1]
参考资料
[1] Aurelien Geron, 王静源, 贾玮, 边蕤, 邱俊涛. 机器学习实战：基于 Scikit-Learn 和 TensorFlow[M]. 北京: 机械工业出版社, 2018: 121-127.
监督学习 | 线性回归 之正则线性模型原理及Sklearn实现相关推荐
- 无监督学习 | GMM 高斯混合聚类原理及Sklearn实现
文章目录 1. 高斯混合聚类 1.1 高斯混合分布 1.2 参数求解 1.3 EM 算法 2. Sklearn 实现 参考文献 相关文章: 机器学习 | 目录 机器学习 | 聚类评估指标 机器学习 | ...
- 监督学习 | 线性回归 之多元线性回归原理及Sklearn实现
文章目录 1. 线性回归 1.1 基本形式 1.2 成本函数 2. w 的计算方式 2.1 标准方程法 2.1.1 普通形式 2.1.2 向量形式 2.1.3 Python 实现 2.1.4 计算复杂 ...
- 监督学习 | 线性分类 之Logistic回归原理及Sklearn实现
文章目录 1. Logistic 回归 1.1 Logistic 函数 1.2 Logistic 回归模型 1.2.1 模型参数估计 2. Sklearn 实现 参考资料 相关文章: 机器学习 | 目 ...
- 监督学习 | 非线性回归 之多项式回归原理及Sklearn实现
文章目录 1. 多项式回归 2. Sklearn 实现 参考资料 相关文章: 机器学习 | 目录 机器学习 | 回归评估指标 监督学习 | 线性回归 之多元线性回归原理及Sklearn实现 监督学习 ...
- 无监督学习 | 层次聚类 之凝聚聚类原理及Sklearn实现
文章目录 1. 层次聚类 1.1 凝聚聚类 1.2 层次图 1.3 不同凝聚算法比较 2. Sklearn 实现 2.1 层次图可视化 参考文献 相关文章: 机器学习 | 目录 机器学习 | 聚类评估 ...
- 无监督学习 | DBSCAN 原理及Sklearn实现
文章目录 1. 密度聚类 2. DBSCAN 2.1 算法原理 3. DBSCAN 优缺点 3.1 优点 3.2 缺点 3.3 与 KMeans 比较 4. SKlearn 实现 5. 在线可视化 D ...
- 监督学习 | SVM 之非线性支持向量机原理
文章目录 1. 非线性支持向量机 1.1 核技巧 1.2 核函数 1.2.1 核函数选择 1.2.2 RBF 函数 参考资料 相关文章: 机器学习 | 目录 机器学习 | 网络搜索及可视化 监督学习 ...
- 监督学习 | SVM 之线性支持向量机原理
文章目录 支持向量机 1. 线性可分支持向量机 1.1 间隔计算公式推导 1.2 硬间隔最大化 1.2.1 原始问题 1.2.2 对偶算法 1.3 支持向量 2. 线性支持向量机 2.1 软间隔最大化 ...
- 线性回归之正则化线性模型
线性回归之正则化线性模型 Ridge Regression 岭回归 Lasso 回归 Elastic Net 弹性网络 Early stopping 1 Ridge Regression (岭回归,又 ...
最新文章
- 游戏编程性能优化--------------------------------------------------------------------------------------...
- GraphQL支持层级结构的query
- 《C++ Primer》7.3.1节练习
- 回文数、括号匹配（栈操作）
- python中合并列表_关于python：如何将两个列表合并到一个列表中？
- SizeOf相关代码
- The example program of C on point
- IPython notebook安装指导
- 如何利用matlab显示图像的方向矢量图
- Android统计图控件之圆饼图
- 掉队于云计算市场是甲骨文裁员的最大原因
- GMT、UTC、DST、CST时区
- RFS实例登录126邮箱/利用cookie登陆百度
- Android对抗反编译，非科班程序员求职经历分享
- 计算机专业试讲10分钟教案,幼儿园10分钟试讲教案
- 完美安装运行Xcelsius 2008 SP3解决方案
- 图形学基础|球谐光照（Spherical Harmonics Lighting）
- tungsten-replicator安装
- Java的LockSupport.park()实现分析（转载）
- FPGA控制W5500完成UDP环回测试