【博弈】 各种博弈的搬运整理
这两天认识了几个组合游戏的基础模型,希望自己能更新下去。。
Ferguson游戏
Description
- Initial
有两个盒子,一个装有 m 颗糖,一个装有 n 颗糖,表示为 (m, n) .
- Step
每次清空一个盒子,将另一个盒子里的糖转移一些过来,并保证两个盒子至少各有一颗糖。
- Win
最后进行转移糖者胜,无法转移糖者败。
Solve
m, n 都为奇数,先手败;m, n 至少一个为偶数,先手胜。
Proof
显然,初始状态为(1, 1),先手必败;
设 max(m, n) = 2,即初始状态为 (1, 2),(2, 1) 或 (2, 2),对于 (1, 2),(2, 1) 先手可以把 1 清空,然后将 2 分为 (1, 1) ,先手胜;对于 (2, 2) ,先手可以把其中一个 2 清空,然后将另一个 2 分为 (1, 1) ,先手胜。符合结论。
设 max(m, n) < k 均符合结论,当 max(m, n) = k :
设 m 与 n 至少一个为偶数(假设m是偶数),则将 n 清空,把 m 分为两个奇数 (a, b) ,由于max(a, b) < k ,因此(a, b) 必败,(m, n) 必胜(利用规则2);
设 m 与 n 均为奇数,则只能把其中一个数分为一个奇数 a ,一个偶数 b ,由于max(a, b) < k ,因此对于任何的方式分解出的(a, b) 均必胜,(m, n) 必败(利用规则1);
故 max(m, n) = k 符合结论。
故对于任意 (m, n) 结论成立。
chomp!游戏
Description
- Initial
有一个 m * n 的棋盘,棋盘的每一个格子用(x, y)表示,最左下角是(1, 1),最右上角是(m, n) ;
- Step
每次可以拿走一个方格,并拿走该方格右边与上边的所有方格。
- Win
谁拿到(1, 1)谁败。
Solve
当 m = n = 1,先手败;除此之外,先手均有必胜策略(先手胜)。
Proof
反证法:
假设后手能取得胜利,那么先手可以第一步拿走(m, n),若后续回合内后手通过拿走(x, y)达到了必胜状态,先手均可以第一步就拿走(x, y)来达到必胜状态。
故不存在后手必胜状态。
由于无法给出构造性证明,所以只能证明先手必胜,而不能给出广义的必胜策略。
约数游戏
Description
- Initial
桌上有 n 个数字:1~n。
- Step
两人轮流在选择一个桌上的数 x ,然后将 x 与 x 的约数都拿走。
- Win
拿去最后一个数的人胜出(无法选择数字的人失败)。
Solve
先手有必胜策略。(先手胜)
Proof
这个游戏是 chomp! 的思想的应用。
假设后手能取得胜利,那么先手可以第一步拿走 1,若后续回合内后手通过拿走 x 达到了必胜状态,先手均可以第一步就拿走 x 来达到必胜状态。
Bash Game(巴什博弈)
Description
- Initial
n 个物品堆成一堆。
- Step
两个人轮流从这堆物品中取物,规定每次至少取一个,最多取 m 个。
- Win
最后取光者得胜。(无法取者败)
Solve
如果 n % (m+1)≠0,则先手必胜。
Proof
如果 n=m+1 , 显然,先手无论取多少,后手均可以将剩余物品一次全取走,所以先手败。
如果 n=k∗(m+1),我们从后手的角度来考虑,设先手第一次取走 x 个物品,那么后手只要再取走 m+1−x 个,此时剩余物品数量变为 (k−1)(m+1) 个,一直重复这个步骤,就可以回到先手面临 n=m+1 的局面,所以还是先手败。相当于进行了k次 n=m+1 的游戏。
如果 n=k∗(m+1)+s,先手一开始取走 s 个物品,那么后手就会面临 n=k∗(m+1) 的局面,所以先手胜。
结论得证。
例题
有一个游戏,在一个n*m的矩阵中起始位置是(1, m),走到终止位置(n, 1);游戏规则是只能向左,下,左下方向移动一步,先走到终点的为获胜者。(HDU 2147,总共有 n + m 的距离要移动,一次最多移动 2 的距离,故判断 (n + m)%2 是否为 0 即可)。
bash博弈变形1——减法博弈:
两个人轮流报数,每次至少报一个,最多报十个,谁能报到100者胜。(先手必胜,第一次报1,类似:HDU 2149)
有一个由n个石子组成的石子堆,两名玩家轮流从中拿走石子,每次拿走石子的个数只能是集合S中的数。拿走最后一枚石子的玩家获胜。(状态转移即可)bash博弈变形2:初始状态下有石子n个,除最后一次外其他每次取物品个数必须在[p,q]之间,最后一次取硬币的人输。(HDU 2897)
这题状态稍微复杂一些,并且胜负条件与之前相反,一般bash博弈里每次取个数可以看作在[1,m]之间,胜负手判断为 n % (1+m),因此我们可以猜想每次取[p,q]的胜负手判断为 n % (p+q),通过验证猜想我们可以发现如下策略:- n=k∗(p+q) 时,先手第一次取 q 个,随后的回合若后手取 x 个,先手再取 p+q−x 个,那么最后就会留给后手 p 个,先手胜。
- n=k∗(p+q)+s 时,则要分情况考虑:
- 若 s 在[1,p]之间,先手取 x,后手可以取 p+q−x ,最后留给先手 s 个,后手胜;
- 若 s 在(p,p+q)之间,先手任取 x 个 (1≤s−x<p),后手取 y 个,先手可以再取 p+q−y ,最后留给后手 s - x 个,先手胜;
//HDU 2897
#include<bits/stdc++.h>
using namespace std;int main()
{int n , p , q ;while ( cin >> n >> p >> q ) {if ( n % ( p + q ) <= p && n % ( p + q ) ) puts( "LOST" ) ;elseputs( "WIN" ) ;}return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Wythoff’s Game(威佐夫博弈)
Description
- Initial
有两堆石子,一堆有 m 个,另一堆有 n 个。
- Step
双方轮流取走一些石子,合法的取法有如下两种:
1. 在一堆石子中取走任意多颗;
2. 在两堆石子中取走相同多的任意颗.
- Win
取走最后一颗石子的人为赢家。
Solve
(1,2)(1,2)(1,2) 与 (2,1)(2,1)(2,1) 视为同一状态,
第 k 个必败状态是 (\lfloor\frac{\sqrt 5 +1}{2}*k \rfloor+k,\lfloor\frac{\sqrt 5 + 1}{2}*k \rfloor)(⌊5√+12∗k⌋+k,⌊5√+12∗k⌋)(⌊5√+12∗k⌋+k,⌊5√+12∗k⌋)。
拓展性质:
令(m(k),n(k))=(\lfloor\frac{\sqrt 5 + 1}{2}*k \rfloor+k,\lfloor\frac{\sqrt 5 + 1}{2}*k \rfloor)(m(k),n(k))=(⌊5√+12∗k⌋+k,⌊5√+12∗k⌋)(m(k),n(k))=(⌊5√+12∗k⌋+k,⌊5√+12∗k⌋),则 m(k) 也表示前 k 个必败状态中没出现的自然数。
每个自然数都会出现在必败状态中且仅会出现一次。
//HDU 1527 模板题
#include<bits/stdc++.h>
using namespace std;int main()
{int a , b ;while ( cin >> a >> b ) {if ( a < b ) swap( a, b ) ;int k = a - b ;int n = (int)( k * ( sqrt(5.0) + 1.0 ) / 2 ) ;bool win = ( n != b ) ;cout << win << endl ;}return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Proof
还是打表吧。。
const int N = 50 ;
bool win[100][100] ;
void init()
{memset( win , false , sizeof win ) ;for ( int i = 1 ; i <= n ; i++ ) win[i][i] = true ;for ( int i = 1 ; i <= n ; i++ ) {for ( int j = i+1 ; j <= n ; j++ ) {if ( !win[i][j] ) {for ( int k = j + 1 ; k <= n ; k++ )win[i][k] = win[k][i] = true ;for ( int k = i + 1 ; k <= n ; k++ )win[k][j] = win[j][k] = true ;for ( int k = 1 ; k <= n ; k++ )win[i+k][j+k] = win[j+k][i+k] = true ;}}}for ( int i = 1 ; i <= n ; i++ )for ( int j = i ; j <= n ; j++ ) {if ( !win[i][j] ) cout << i << ' ' << j << endl ;}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
Fibonacci’s Game (斐波那契博弈)
Description
- Initial
有一堆个数为 n >= 2 的石子。
- Step
双方轮流取石子,满足以下条件:
1. 先手不能在第一次把所有的石子取完;
2. 之后每次可以取的石子数介于 1 到对手刚取的石子数的 2 倍之间(包含 1 和对手刚取的石子数的 2 倍)。
- Win
取走最后一个石子的人为赢家。
Solve
如果 n 是斐波那契数,则后手胜;反之,先手胜。
\\HDU 2516 模板题
#include<bits/stdc++.h>
using namespace std;const string win[2] = { "Second win" , "First win" } ;
long long fib[100] ;
int init()
{fib[0] = 1 ; fib[1] = 1 ;for ( int i = 2 ; i < 100 ; i++ ) {fib[i] = fib[i-1] + fib[i-2] ;if ( fib[i] > ( 1LL << 35 ) ) return i ;}return 100 ;
}
int main()
{int n ; int len = init() ;while ( cin >> n && n ) {int ok = 1 ;for ( int i = 0 ; i <= len ; i++ ) {if ( fib[i] == n ) {ok = 0 ;break ;}}cout << win[ok] << endl ;}return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
Proof
Zeckendorf定理:任何正整数可以表示为若干个不连续的 Fibonacci 数之和。
先手必须从 <= n / 3 的数量开始取(例如第一次取的数量 > n/3,那么后手可以直接取完所有剩下石子)
于是。。。太绕了!
还是请看Acdream大神的吧。。http://blog.csdn.net/acdreamers/article/details/8586135
Nim游戏(待施工)
Description
有三堆各若干个物品,两个人轮流从某一堆取任意多的
物品,规定每次至少取一个,多者不限,最后取光者得胜。
Solve
介绍这个游戏的太多了。。偷个懒
具体解法就是异或异或!
以下内容来自转载:
博弈问题简介
所讨论的博弈问题满足以下条件:
- 玩家只有两个人,轮流做出决策
- 游戏的状态集有限,保证游戏在有限步后结束,这样必然会产生不能操作者,其输
- 对任何一种局面,胜负只决定于局面本身,而与轮到哪位选手无关
一般称满足以上条件的游戏称为ICG,比如我们将要讨论的Nim游戏。作为一个对比,我们平时玩的象棋就不属于ICG,因为它不满足第三条。
ICG具有两个状态,我们称为必胜态和必败态,他们的关系:
后继状态能达到必败的状态为必胜态
所有后继状态都不为必败态,则其为必败态
第二条也可以换一种说法:后继状态都是必胜态,则其为必败态。 所以我们可以看出一个状态不是必胜态,就是必败态。
取石子游戏NIM
取石子游戏是一个古老的博弈游戏,发源于中国,它是组合数学领域的一个经典问题。它有许多不同的玩法,基本上是两个玩家,玩的形式是轮流抓石子,胜利的标准是抓走了最后的石子。
玩家设定: 先取石子的是玩家A,后取石子的是玩家B。
经典的三种玩法
一、巴什博奕(Bash Game),有1堆含n个石子,两个人轮流从这堆物品中取物,规定每次至少取1个,最多取m个。取走最后石子的人获胜。
二、尼姆博奕(Nimm Game),有k堆各n个石子,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限。取走最后石子的人获胜。
三、威佐夫博奕(Wythoff Game),有2堆各n个石子,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取1个,多者不限。取走最后石子的人获胜。POJ1067
平衡状态的概念:
引入一个概念,平衡状态,又称作奇异局势。当面对这个局势时则会失败。任意非平衡态经过一次操作可以变为平衡态。每个玩家都会努力使自己抓完石子之后的局势为平衡,将这个平衡局势留给对方。因此,玩家A能够在初始为非平衡的游戏中取胜,玩家B能够在初始为平衡的游戏中取胜。
http://blog.csdn.net/pipisorry/article/details/39249337
取石子游戏不同玩法的解决方案
玩法一(1堆n个石子每次最多取m个)
即,若n=k*(m+1),则后取着胜,反之,存在先取者获胜的取法。n%(m+1)==0. 先取者必败。
一般的奇异局势是n=(m+1)*i,其中i为自然数,即n%(m+1)=0,面对这种情况无论我怎么取,对方总可以将其恢复为n%(m+1)=0,一直到n=(m+1)局势。
就是把当前面对的非奇异局势变为奇异局势留给对方。如果当前的石子个数为(m+1)*i+s,那么就将s个石子取走,使其达到奇异局势。
两个人轮流报数,每次至少报一个,最多报十个,谁能报到100者胜。(<=>从一堆100个石子中取石子,最后取完的胜)
最后一个奇异局势是n=(0)。一种奇异局势是,n=(m+1),那么无论我取走多少个,对方都能够一次取走剩余所有的物品取胜。
http://blog.csdn.net/pipisorry/article/details/39249337
玩法二(k堆石子每次只从1堆取)
简化问题:有三堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
拓展
任给N堆石子,两人轮流从任一堆中任取(每次只能取自一堆),取最后一颗石子的人获胜,问先取的人如何获胜?
根据上面所述,N个数异或即可。如果开始的时候T=0,那么先取者必败,如果开始的时候T>0,那么只要每次取出石子使得T=0,即先取者有获胜的方法。
最后一个奇异局势是(0,0...,0)。另一个奇异局势是(n,n,0...0),只要对手总是和我拿走一样多的物品,最后会面对(0,0...,0)。
http://blog.csdn.net/pipisorry/article/details/39249337
玩法三(2堆石子每次从一或两堆取一样数目的石子)
前几个奇异局势是:(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。。。
Ak = [k*(1+sqrt(5.0)/2]
Bk = Ak + k
其中k=0,1,2,...,n ,方括号表示int取整函数。
有了这个通项式子,逆向的,对于某一个局势,只需要判断其A是否是黄金分割数的某个k的倍数,然后再确认B是否等于A+k即可。
奇妙的是其中出现了黄金分割数(1+√5)/2 = 1.618...,因此,由ak,bk组成的矩形近似为黄金矩形,由于2/(1+√5)=(√5-1)/2,可以先求出j=[a(√5-1)/2],若a=[j(1+√5)/2],那么a = aj,bj = aj + j,若不等于,那么a = aj+1,bj+1 = aj+1+ j + 1,若都不是,那么就不是奇异局势。然后再按照上述法则进行,一定会遇到奇异局势。
我们会发现这个序列的规律,设序列第k个奇异局势元素为(Ak,Bk),k为自然数。那么,初始条件k=0时是,A0=B0=0,递推关系为下一个奇异局势的Ak是未在前面出现过的最小自然数,且Ak = Bk + k。
变种玩法
“皇后登山”游戏,在空的围棋棋盘上放一个棋子,该棋子每次只能向上或向右或沿对角线向右上方向移动(相似国际象棋),可以移动任意格,但不能不移动,两人轮流移动棋子,先将棋子移动到右上角者赢,问先移棋者的必胜策略。《智力游戏中的数学方法》。code:

- /****************************************************************************/
- /* 编程之美 - NIM捡石子问题 皮皮 2014-9-10 */
- /****************************************************************************/
- #include <assert.h>
- #include <stdio.h>
- #include <math.h>
- /* 黄金分割数最优算法 */
- static int nim(int x, int y){
- double a = (sqrt(5.0) + 1) / 2; //goldenNum 1.618...
- int n = abs(x - y); //bn - an
- x = x < y? x : y; //取小者
- return ( x != int(a * n) );
- }
- int main(){
- int x, y;
- while(scanf("%d%d", &x, &y) == 2)
- printf("%d\n", nim(x, y));
- return 0;
- }

http://blog.csdn.net/pipisorry/article/details/39249337
尼姆博奕的分解解释
有一堆石子,两个人轮流从石子堆中拿走任意数量的石子,但不能不拿。谁不能拿谁为输。
显然,这个游戏中只要先手把所有石子都拿完,那么后手就一定输了。因为此时没有石子,后手无法进行合法的操作。
有两堆石子,分别为a,b个石子,每个玩家只能选一堆,然后拿走任意正整数个石子,谁不能拿谁输。
我们先讨论一个特殊情况,即:a=b时,此时后手是必胜的。此时不管先手怎么操作,我们只要选择与先手不同的那堆,然后进行与先手相同的操作即可。
这里a=b即为我们所说的必败态。而当a≠b时,我们肯定可以拿比较多的那堆,使之和少的那堆数量相等,此时我们就必胜了,所以此时就为必胜态。
当有三堆,数量分别为a,b,c时,我们就比较不好分析了。当然我们可以直接搜索得到最后结果,但是当我们拓展到n堆时(相当于二、尼姆博奕),此时我们搜索也变得不可行了。
sg函数
由于只能更改一堆的状态,无论哪一位的1被改变,那么原来那位上1的奇偶个数一定会改变,所以就会变为必胜态。
拓展:?
综合一、三
任给N堆石子,两人轮流从任一堆中任取(每次只能取自一堆),规定每方每次最多取K颗,取最后一颗石子的一方获胜.问先取的人如何获胜?
与上面的问题比,这个更复杂一些,我们可以这样做
令Bi=Ai mod(K+1)
定义T‘=B1 xor B2 xor ... xor Bn
如果T‘=0 那么没有获胜可能,先取者必败
如果T’>0 那么必然存在取的方法,使得T‘=0,先取者有获胜的方法
假设对方取了在Ai中取了r<=K个
如果Ai中剩下的石子多于K 那么就在Ai中取走K+1-r个则Bi不变 T‘还是0
如果Ai<=K 那么我们需要重新计算Bi和T‘ 按照上面的方法来做就可以了
固定多个数目取石子
Alice和Bob在玩一个取石子游戏,规则如下:
1,Alice先手,两人轮流取,每次可以取1/2/4颗。
2,取走最后一颗石子的人胜出。
问题:
1,共有16颗石子时,谁将胜出?
2,共有n (n>=1) 颗石子时,谁将胜出?
分析:
Alice的必胜态:
当Alice取完本轮石子后,剩下的石子为3的倍数(3*n),那么无论Bob怎么取,Alice都会赢。
简单解释如下:
①n = 1时,即Alice取完后只剩下3颗,那么无论Bob怎么取,Alice下次取都会取到最后一颗,会赢。
②n >1时,即Alice取完后剩下3*n颗,当Bob取完后,剩下的石子数量总可以表示为:
3*k+1 或 3*k + 2(k >= 0),那么此时Alice可以将剩下的石子数重新变为3的倍数,如此递推下去。
...
最终剩下石子数量变为3。也就是说,只要Alice取完后,剩下的石子数是3的倍数,那么Alice肯定会赢。
即n%3==0时Alice输,否则赢(都按最优策略取石子)
简化约数博弈
两个人轮流在黑板上写一个不大于10的正整数。规定不准把已经写过的数的约数再写出来。谁最后没写的了谁就输了。问是先写的人必胜还是后写的人必胜,必胜策略是什么。
分析:先写者有必胜策略。他可以先写下数字6,现在就只剩下4、5、7、8、9、10可以写了。把剩下的6个数分成三对,分别是(4,5)、(7,9)、(8,10),每一对里的两个数都不成倍数关系,且它们各自的倍数(如果出现过)必然是同时出现。因此不管你写什么数,我就写它所在的数对里的另一个数,这样可以保证我总有写的。
[小学奥赛的经典题目]
约数博弈
甲乙两个人玩一个博弈游戏。游戏初始状态包含1-n, 这n个正整数。
甲乙两个人轮流玩这个游戏。每轮游戏中,游戏者任意选择一个还存在的数,然后删掉它和它所有的约数。
谁最后没有数可删,谁就输掉了。
问题:他们都足够聪明,甲先开始,请分析谁有必胜策略?
分析:先手有必胜策略。这个证明不是构造性的,也就是说没有给出先手怎么下才能赢。反证法:假设后手B有必胜策略,而先手A第一次取数1,B取了一个数x是必胜策略,然而A完全可以第一次取x(同时也必取了1)是必胜策略。故B必没有必胜策略。
不过lz有一种比较暴力的策略不知对否:将所有数据分成数对(除数1外每个数对都不是约数),对手取完一个数后,如果剩下的是奇数,则取一个合适的数让剩下的数可以重新分对,如果剩下的是偶数,则取一个合适的数(这个数的约数有奇数个),剩下的数仍可以重新分对。这样对手不管取哪个数,总有一个与对手取的数不是约数的数可以给你取。
Note:整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。一个数的约数必然包括1及其本身。任何正整数都是0的约数。
变型:考虑一个新的规则“不准写数字1”。如果加上这个新规则后先写者有必胜策略,那么这个策略对于原游戏同样适用(因为1是所有数的约数,本来就不能写);如果在新规则下后写者必胜,则原游戏中的先写者写下数字1,然后他就变成了新规则下的后写者。于是不管怎么样,先写者总是有必胜策略。
只要是双方共用状态(合法的决策完全相同)的对弈游戏,其中一方肯定有必胜策略。棋局的任一状态只有两种,面对这个棋局的人要么必胜要么必败。考虑这样的一个递推关系:如果一个状态是必胜态,那至少有一种走法能走成一个必败态留给对方;如果一个状态是必败态,那它怎么走都只能走到必胜态。运用这样的关系,我们可以自底向上推出初始状态是必胜还是必败。
这种分析方法有一种很形象的名字叫做Strategy-stealing,它的另一个经典例子是Chomp游戏。上面所举的例子都是双方共用状态的游戏(ICG游戏),因此至少有一方存在必胜策略。对于其它一些非ICG游戏,我们也可以用类似的方法证明后手不可能有必胜策略(但在这里并不能说明先手一定必胜)。比如对于井字棋游戏,假设后手有必胜策略,那先手就随便走一步,以后就装成是后手来应对。如果在哪一步需要先手在已经下过子的地方落子,他就再随便走一步就是了。这种证明方法成立的前提就是,多走一步肯定不是坏事。事实上,对于所有这种“多走一步肯定不是坏事”的且决策对称的游戏,我们都可以证明后手是没有必胜策略的。
[博弈问题入门]
Chomp!博弈(巧克力游戏)
有一个n*m的棋盘,每次可以取走一个方格并拿掉它右边和上面的所有方格。拿到左下角的格子(1,1)者输,如下图是8*3的
棋盘中拿掉(6,2)和(2,3)后的状态。

结论:答案是除了1*1的棋盘,对于其他大小的棋盘,先手总能赢。
分析:有一个很巧妙的证明可以保证先手存在必胜策略,可惜这个证明不是构造性的,也就是说没有给出先手怎么下才能赢。
证明如下:如果后手能赢,也就是说后手有必胜策略,使得无论先手第一次取哪个石子,后手都能获得最后的胜利。那么现在假设先手
取最右上角的石子(n,m),接下来后手通过某种取法使得自己进入必胜的局面。但事实上,先手在第一次取的时候就可以和
后手这次取的一样,进入必胜局面了,与假设矛盾。
约数和倍数博弈
给定的一些自然数,如 2,3,4,5,6,。。。,两人依次拿数,连同该数的约数和倍数一起拿掉,如拿2要连4,6一起拿掉;拿6要连带2,3一起拿掉。最后总有一人没法拿了(因为数都拿光了),就算输。
举例:
2,3,4
先拿者不管怎样拿都是输。先出2题:
题1:初始数据 2,3,4,5,6,7,8,9,10 共9个数字。
题2:初始数据 2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 共17个数字。
问:先拿者赢还是输,如果赢的话,第一步怎样拿?
[智能博弈题]
其它类似题型
POJ1740A New Stone Game
MIPT 100 Nim Game -- who is the winner?
POJ 1704 Georgia and Bob
楼梯Nim:就是把楼梯上的棋子两两绑定,他们之间的距离看成是一堆石子,于是就等同于我们之前讨论的经典Nim游戏了。
Moore’s Nimk:广义的Nim游戏。有n堆石子,每次最少选一堆,最多选m堆,每堆都可以拿任意正整数个石子。我们把每堆石子都写成二进制的形式,然后从低位到高位求每一位1的和。如果每一位1的和sum%(m+1)=0此时为必败态。显然,当m=1时就变成了我们最开始所讨论的最基础的Nim游戏了。
翻硬币游戏:这类题目比较复杂,一般打表找规律。
图的删边游戏
http://blog.csdn.net/pipisorry/article/details/39249337
附录
有两堆石子,不妨先认为一堆有10,另一堆有15个,双方轮流取走一些石子,合法的取法有如下两种:
1)在一堆石子中取走任意多颗;
2)在两堆石子中取走相同多的任意颗;
约定取走最后一颗石子的人为赢家,求必败态(必胜策略)。
这个可以说是MR.Wythoff(于1907年提出此游戏)一生全部的贡献。不知道高斯取整函数与Beatty定理,所做的只能是找规律而已。可以先在http://www.cut-the-knot.org/pythagoras/withoff.shtml玩几局。
简单分析一下,容易知道两堆石头地位是一样的,我们用余下的石子数(a,b)来表示状态,并画在平面直角坐标系上。
用定理: 有限个结点的无回路有向图有唯一的核 中所述的方法寻找必败态。先标出(0,0),然后划去所有(0,k),(k,0),(k,k)的格点;然后找y=x上方未被划去的格点,标出(1,2),然后划去(1,k),(k,2),(1+k,2+k),同时标出对称点(2,1),划去(2,k),(1,k),(2+k,1+k);然后在未被划去的点中在y=x上方再找出(3,5)。。。按照这样的方法做下去,如果只列出a<=b的必败态的话,前面的一些是(0,0),(1,2),(3,5),(4,7),(6,10),…
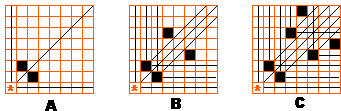
接下来就是找规律的过程了,忽略(0,0),记第n组必败态为(a[n],b[n])
命题一:a[n+1]=前n组必败态中未出现过的最小正整数
[分析]:如果a[n+1]不是未出现的数中最小的,那么可以从a[n+1]的状态走到一个使a[n+1]更小的状态,和我们的寻找方法矛盾。
命题二:b[n]=a[n]+n
[分析]:归纳法:若前k个必败态分别为 ,下证:第k+1个必败态为
从该第k+1个必败态出发,一共可能走向三类状态,从左边堆拿走一些,从右边堆拿走一些,或者从两堆中拿走一些.下面证明这三类都是胜态.
情况一:由命题一,任意一个比a[k+1]小的数都在之前的必败态中出现过,一旦把左边堆拿少了,我们只要再拿成那个数相应的必败态即可。
情况二(从右边堆拿走不太多):这使得两堆之间的差变小了,比如拿成了 ,则可再拿成
;
情况二(从右边堆拿走很多):使得右边一堆比左边一堆更少,这时类似于情况一,比如拿成了 (其中a[m] ;
情况三:比如拿成 ,则可再拿成
.
综上所述,任何从 出发走向的状态都可以走回核中.故原命题成立.
以上两个命题对于确定(a[n],b[n])是完备的了,给定(0,0)然后按照这两个命题,就可以写出(1,2),(3,5),(4,7),…
这样我们得到了这个数列的递推式,以下我们把这两个命题当成是(a[n],b[n])的定义。
先证明两个性质:
性质一:核中的a[n],b[n]遍历所有正整数。
[分析]:由命题一,二可得a[n],b[n]是递增的,且由a[n]的定义显然。
性质二:A={a[n]:n=1,2,3,…},B={b[n]:n=1,2,3,…},则集合A,B不交。
[分析]:由核是内固集,显然。
实际上a[n]和b[n]就是一个Beatty序列。
(Betty 定理)
如果存在正无理数 A, B 满足 1/A + 1/B = 1,那么集合 P = { [A*t], t ∈ Z+}、Q = { [B*t], t ∈ Z+} 恰为集合 Z+ 的一个划分,即:P ∪ Q = Z+,P ∩ Q = ø。证明见附录2。
考虑到Betty定理中“恰为Z+的划分”这一说,这意味着,Z+中的每个数都恰好出现一次,与上述矩阵的性质十分吻合。
于是我们猜想每一行第一列的数满足 [Φi] 的形式,得到每一行第二列的数为 [Φi] + i = [Φi + i] = [(Φ + 1)i]
我们的目的是要让 Z+ 中每个数都在这个矩阵中出现,于是考虑到 Betty 定理的条件,Φ 和 (Φ + 1) 应满足 1/Φ + 1/(Φ + 1) = 1。解这个方程,我们得到 Φ = (sqrt(5) + 1) / 2,于是 Φ + 1 = (sqrt(5) + 3) / 2。 ,到此,我们找到了该必败态的通项公式。
实际上这组Beatty序列还有一些别的性质,比如当一个数是Fibonacci数的时候,另一个数也是Fibonacci数;而且两者的比值也越来越接近黄金比,这些性质在得到通项公式之后不难证明。
启示:首先用定理所说的方法找核,然后给出核的规律(递推,或是通项)并且证明。
附上一张对应的必败态图

2.Betti theorem:
设a、b是正无理数且1/a+1/b=1。记P={[na]|n为任意的正整数},Q={[nb]|n为任意的正整数},([x]'指的是取x的整数部分)则P与Q是Z+的一个划分,即P∩Q为空集且P∪Q为正整数集合Z+。
证明:
因为a、b为正且1/a+1/b=1,则a、b>1,所以对于不同的整数n,[na]各不相同,类似对b有相同的结果。因此任一个整数至多在集合P或Q中出现一次。
* 现证明P∩Q为空集(反证法):假设k为P∩Q的一个整数,则存在正整数m、n使得[ma]=[nb]=k。即k < ma、nb<k+1,等价地改写不等式为
m/(k+1)< 1/a < m/k及n/(k+1)< 1/b < n/k。相加起来得 (m+n)/(k+1) < 1 < (m+n)/k,即 k < m+n < k+1。这与m、n为整数有矛盾,所以P∩Q为空集。
*现证明Z+=P∪Q:已知P∪Q是Z+的子集,剩下来只要证明Z+是P∪Q的子集。(反证法)假设Z+\(P∪Q)有一个元素k,则存在正整数m、n使得[ma]< k <[(m+1)a]、[nb]< k <[(n+1)b]。 由此得ma < k ≦[ (m+1)a]-1<(m+1)a -1(因为a是无理数),类似地有nb < k ≦[ (n+1)b]-1<(n+1)b -1。等价地改写为 m/k < 1/a < (m+1)/(k+1)及n/k < 1/b < (n+1)/(k+1)。两式加起来,得
(m+n)/k < 1 < (m+n+2)/(k+1),即m+n < k < k+1 < m+n+2。这与m, n, k皆为正整数矛盾。
所以Z+=P∪Q。[贝蒂定理]
from:http://blog.csdn.net/pipisorry/article/details/39249337
ref:http://www.cnblogs.com/celia01/archive/2011/11/15/2250171.html
http://blog.csdn.NET/ojshilu/article/details/16812173
http://yjq24.blogbus.com/logs/42826226.html
POJ 1067 取石子游戏
1.13 NIM(3)两堆石头的游戏
状态作为结点可以画一张有向图
编程之美读书笔记_1.13 NIM(3)两堆石头的游戏
编程之美1.13——NIM(3)两堆石头的游戏
尼姆博奕(Nimm Game)
博弈算法入门小节 1536 1517 1907
转自: http://blog.csdn.net/qq_33765907/article/details/51174524http://blog.csdn.net/qq_15714857/article/details/49691585
【博弈】 各种博弈的搬运整理相关推荐
- 读书笔记: 博弈论导论 - 16 - 不完整信息的动态博弈 信号传递博弈
读书笔记: 博弈论导论 - 16 - 不完整信息的动态博弈 信号传递博弈 信号传递博弈(Signaling Games) 本文是Game Theory An Introduction (by Stev ...
- 博弈——通过博弈思想解决的问题(hdu1847,2147)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=1847 题目描述: 1. 总共n张牌: 2. 双方轮流抓牌: 3. 每人每次抓牌的个数只能是2的 ...
- 博弈——Nim博弈(hdu2176,1850,1851,1907,1849)
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=2176 http://acm.hdu.edu.cn/showproblem.php?pid=1850 ...
- java博弈,人机博弈小游戏(Java)
人机博弈小游戏 实现功能 电脑随机出拳 玩家任意出拳 五局三胜制 可判断最终赢家 下面展示 代码. // A code block var foo = 'bar'; // An highlighted ...
- bzoj 4131: 并行博弈(博弈)
4131: 并行博弈 Time Limit: 10 Sec Memory Limit: 256 MB Submit: 42 Solved: 29 [Submit][Status][Discuss] ...
- 博弈论学习之巴什博弈,尼姆博弈, sg博弈
博弈论真是一个神奇的东西,感觉和博弈论厉害的人玩游戏绝对会输. 这个博客讲的很好很全面 此类问题一般有如下特点: 1.博弈模型为两人轮流决策的非合作博弈.即两人轮流进行决策,并且两人都使用最优策略来获 ...
- 博弈基础与例题分析(巴什博弈威佐夫博弈尼姆博奕 斐波那契博弈SG博弈)
文章目录 巴什博弈Bash Game 威佐夫博弈Wythoff Game 尼姆博奕 斐波那契博弈:算法如其名 SG博弈 图 mex(minimal excludant)运算 获得sg表 应用 A Br ...
- 模式识别 计算机博弈,计算机博弈新题材
计算机博弈新题材 中国象棋这一古老的游戏在计算机技术的带领下,我们可以从容的在网上与千里之外的任何人对奕,也可以和象棋软件进行人机对战. 我们知道首先需要把中国象棋编好程序建立一个游戏网站,在这个游戏 ...
- 投资博弈(协调博弈)
投资博弈: 情景:现在每人有10元,两种方式 一种选择不选择投资,收益为0,不损失,不获利 一种选择投资,如果投资人数超过总投资人数的90%,那么投资的每个人会获利 5元,否则失去全部 ...
最新文章
- python123数字形式转换_【Python系统学习02】数据类型与类型转换
- 数据结构源码笔记(C语言):栈的基本操作
- JavaScript实现LongestIncreasingSubsequence最长递增子序列算法(附完整源码)
- C语言merge sort归并排序算法(附完整源码)
- c语言十佳运动员有奖评选系统_2019年沃德十佳内饰解读
- 分布式系统的唯一ID
- oracle函数总结
- Ubuntu学习 mkdir
- 2020腾讯软件测试实习面经
- editormd文件上传
- 知道路径,如何下载服务器端的.frx文件
- lwj_C#_homework get set 属性
- 今天把中国建设银行APP4.2.1版iOS客户端里所有的功能都点了一遍
- python自由落体_pymunk教程_自由落体小球_Pymunk滑动和铰接演示教程
- 【医疗图像分割】Deep neural networks for the detection and segmentation of the retinal fluid in OCT images.
- Go语言泛型工具go2go
- 【个人学年总结】大一——“蛰伏”的一年
- java微服务开发(基础环境篇)
- 太阳能板最大面积js
- JS函数的参数(arguments)的使用
热门文章
- 推荐BMS锂电池管理使用KT6368A蓝牙模块芯片
- 关于电路的竞争与冒险问题详解
- 胡策day 10.26 T2 人、镜子与墙
- 计算机cap怎么学,6大学计算机大学计算机CAP.pdf
- vscode用tensorboard报错 We failed to start a TensorBoard session due to the following error: Command fa
- python项目源代码-python项目源码
- 如何快速在一段字符串中提取想要的字符
- C++实现人员工资管理系统
- 监督学习和无监督学习(概念)
- 手机吃鸡语音服务器异常是怎么回事,《绝地求生》新版本里实用功能介绍 卡语音怎么解决...
