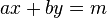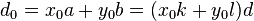poj 1061 (扩展欧几里德算法)
首先先抛出一个例题:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 89761 | Accepted: 16131 |
Description
我们把这两只青蛙分别叫做青蛙A和青蛙B,并且规定纬度线上东经0度处为原点,由东往西为正方向,单位长度1米,这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是x,青蛙B的出发点坐标是y。青蛙A一次能跳m米,青蛙B一次能跳n米,两只青蛙跳一次所花费的时间相同。纬度线总长L米。现在要你求出它们跳了几次以后才会碰面。
Input
Output
Sample Input
1 2 3 4 5
Sample Output
4
涉及知识点:ext_gcd
代码如下:
#include<stdio.h>
#include<math.h>
#define LL long longLL extend_gcd(LL a, LL b, LL &x, LL &y)
{if(b==0){x = 1;y = 0;return a;}LL d = extend_gcd(b, a%b, x, y);LL t = x;x = y;y = t-a/b*y;return d;
}int main()
{LL x, y, n, m, L;LL a,b,c,d;while(~scanf("%lld%lld%lld%lld%lld", &x, &y, &m, &n, &L)){LL p,q;a=n-m, b=L, c = x-y;d = extend_gcd(a, b, p, q);if(c%d!=0) printf("Impossible\n");else{p = p*(c/d);p = (p%b + b)%b;printf("%lld\n", p);}}return 0;注意:
ext_gcd模板求得的只是 当 ax + by = gcd(a,b)时,x 和 y 的值。 但是当ax ' + b y' = c 如果有解,则应满足以下情况:,c能够整除gcd(a, b),也就是c = k *(gcd(a, b)) 其中k为整数。那么此时的 x' 就等于kx, y' 就等于 ky,即 x' = kx, y = ky',对应文中代码部分为: p = p*(c/d);。如果想求最小正整数解的话,就要加上 p = (p%b + b)%b 了。
—————————————————————————————————————————————————————————————————————————————
今天看了一下gcd算法,本来学的教材上有这个,但不知道还叫欧几里德算法,于是又重新看了一边,搜的时候没想到还有新的收获,又看到了拓展欧几里德算法。
先说一下gcd吧,也叫辗转相除法。给定两个数 a,b , 求两个数中的最大公约数。
int gcd(int n, int m) // n>m
{
if(n%m == 0)
return m;
else
return (m, n%m);
}
思路比较简单,两个数(a, b,其中a>b)的最大公约数就等于其中较小数(b)和(a%b)这两个数的最大公约数。
最小公倍数等于 两个数的乘积除以两个数的最大公约数。
—————————————————————————————————————————————————————————————————————————————
再说一下extend_gcd( 拓展欧几里得算法),ext_gcd 算法由裴蜀定理中得出:
知识点: 在数论中,裴蜀等式或裴蜀定理是一个关于最大公约数(或最大公约式)的定理。裴蜀定理得名于法国数学家艾蒂安·裴蜀,说明了对任何整数 、
、 和它们的最大公约数
和它们的最大公约数 ,关于未知数
,关于未知数 和
和 的线性丢番图方程(称为裴蜀等式):
的线性丢番图方程(称为裴蜀等式):
有整数解时当且仅当m是d 的倍数。裴蜀等式有解时必然有无穷多个整数解,每组解 、
、 都称为裴蜀数,可用扩展欧几里得算法求得。
都称为裴蜀数,可用扩展欧几里得算法求得。
例如,12和42的最大公约数是6,则方程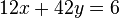 有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。
有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。
特别来说,方程  有整数解当且仅当整数a和b互素。
有整数解当且仅当整数a和b互素。
裴蜀等式也可以用来给最大公约数定义: 其实就是最小的可以写成
其实就是最小的可以写成 形式的正整数。这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。
形式的正整数。这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。
历史:历史上首先证明关于整数的裴蜀定理的并不是裴蜀,而是17世纪初的法国数学家克劳德-加斯帕·巴歇·德·梅齐里亚克(Claude-Gaspard Bachet de Méziriac)。他在于1624年发表的著作《有关整数的令人快乐与惬意的问题集》(Problèmes plaisans et délectables qui se font par les nombres)第二版中给出了问题的描述和证明[1]。
然而,裴蜀推广了梅齐里亚克的结论,特别是探讨了多项式中的裴蜀等式,并给出了相应的定理和证明[2]。
证明过程如下:
整数中的裴蜀定理
对任意两个整数 、
、 ,设
,设 是它们的最大公约数。那么关于未知数
是它们的最大公约数。那么关于未知数 和
和 的线性丢番图方程(称为裴蜀等式):
的线性丢番图方程(称为裴蜀等式):
有整数解(x,y) 当且仅当m 是d 的倍数。裴蜀等式有解时必然有无穷多个解。
如果  和
和 中有一个是0,比如
中有一个是0,比如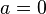 ,那么它们两个的最大公约数是
,那么它们两个的最大公约数是 。这时裴蜀等式变成
。这时裴蜀等式变成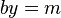 ,它有整数解(x,y) 当且仅当m 是d 的倍数,而且有解时必然有无穷多个解,因为
,它有整数解(x,y) 当且仅当m 是d 的倍数,而且有解时必然有无穷多个解,因为 可以是任何整数。定理成立。
可以是任何整数。定理成立。
以下设  和
和 都不为0。
都不为0。
设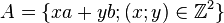 ,下面证明
,下面证明 中的最小正元素是
中的最小正元素是 与
与 的最大公约数。
的最大公约数。
首先,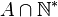 不是空集(至少包含
不是空集(至少包含 和
和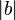 ),因此由于自然数集合是良序的,
),因此由于自然数集合是良序的, 中存在最小正元素
中存在最小正元素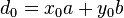 。考虑A中任意一个正元素p(
。考虑A中任意一个正元素p(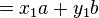 )对
)对 的带余除法:设
的带余除法:设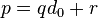 ,其中q 为正整数,
,其中q 为正整数,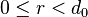 。但是
。但是
因此 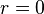 ,
,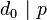 。也就是说,A中任意一个正元素p都是
。也就是说,A中任意一个正元素p都是 的倍数,特别地:
的倍数,特别地: 、
、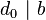 。因此
。因此 是
是 和
和 的公约数。
的公约数。
另一方面,对  和
和 的任意正公约数
的任意正公约数 ,设
,设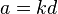 、
、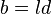 ,那么
,那么
因此 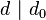 。所以
。所以 是
是 和
和 的最大公约数。
的最大公约数。
在方程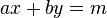 中,如果
中,如果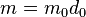 ,那么方程显然有无穷多个解:
,那么方程显然有无穷多个解:
-
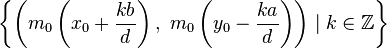 。
。
相反的,如果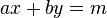 有整数解,那么
有整数解,那么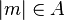 ,于是由前可知
,于是由前可知 (即
(即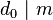 )。
)。
m=1时,方程有解当且仅当a、b互质。方程有解时,解的集合是
-
 。其中
。其中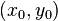 是方程
是方程 的一个解,可由辗转相除法得到。
的一个解,可由辗转相除法得到。
所有解中,有且仅有一个解(x,y) 满足 ,
,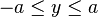 。
。
拓展欧几里德算法:见链接 http://zh.wikipedia.org/wiki/%E6%89%A9%E5%B1%95%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%AE%97%E6%B3%95
转载于:https://www.cnblogs.com/6bing/p/3931241.html
poj 1061 (扩展欧几里德算法)相关推荐
- 青蛙的约会(POJ 1061 扩展欧几里德算法)
POJ 1061 青蛙的约会 扩展欧几里德算法简单介绍及应用 题目大意: 两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面.它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳, ...
- 集训笔记---扩展欧几里德算法(POJ NO.1061 青蛙的约会 有点烦人小跳蛙gcd)
又在搬砖,本来以为这是一个追及问题,后来发现数据好像并不是那么个意思,后来把方程列出来,经过一个去模的操作,我们其实可以找到一点线索,那就是,一个经过变形的二元一次方程,那么在这种情况下,就可以利用扩 ...
- poj 2115 C Looooops(扩展欧几里德算法)
题意: 对于for(i=A ; i!=B ;i+=C)循环语句,问在k位存储系统中循环几次才会结束. 比如:当k=4时,存储的数 i 在0-15之间循环.(本题默认为无符号) 若在有限次内结束,则输出 ...
- 欧几里德算法 扩展欧几里德算法
欧几里德算法 欧几里德算法又称辗转相除法,是指用于计算两个正整数a,b的最大公约数. 计算公式:gcd(a,b) = gcd(b,a mod b). 算法实现: public static int g ...
- 扩展欧几里德算法详解
转自:http://blog.csdn.net/zhjchengfeng5/article/details/7786595 扩展欧几里德算法 谁是欧几里德?自己百度去 先介绍什么叫做欧几里德算法 有两 ...
- 欧几里德与扩展欧几里德算法——密码学笔记(五)
一.欧几里德算法 又称辗转相除法,用于计算两个整数a,b的最大公约数. 基本算法:设a=qb+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd(b,a% ...
- 欧几里德算法与扩展欧几里德算法
欧几里德算法 欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数. 基本算法:设a=qb+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd( ...
- (扩展欧几里德算法)zzuoj 10402: C.机器人
10402: C.机器人 Description Dr. Kong 设计的机器人卡尔非常活泼,既能原地蹦,又能跳远.由于受软硬件设计所限,机器人卡尔只能定点跳远.若机器人站在(X,Y)位置,它可以原地 ...
- Bailian2793 孙子问题【扩展欧几里德算法+中国剩余定理】
2793:孙子问题 总时间限制: 15000ms 内存限制: 65536kB 描述 我国古代<孙子算经>中,记有如下算题:"今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩 ...
- 欧几里德算法 扩展欧几里德算法 求解丢番图方程
欧几里德算法 即辗转相除法,计算整数A, B最大公约数. 基本算法:设 a = kb + r,其中a,b,k,r都是整数,则 gcd(a,b) = gcd(b,r),即 gcd(a,b) = gcd( ...
最新文章
- 兼容性—IE6/7下带有overflow:hidden属性的父级元素包不住带有position:relative属性的子元素...
- 笔记:Tensor RPCA: Exact recovery of corrupted low-rank tensors via convex optimization
- Excel列数和列字母的转换(column number 和 column letters 互转)
- C#操作HttpClient工具类库
- C语言,C#语言求100-999内的水仙花数源程序
- DP专练1( [NOIP 2003]加分二叉树 + 太空梯 )
- HDU - 6383 百度之星2018初赛B 1004 p1m2(二分答案)
- VDI序曲二十七 IE7,IE8,IE9应用程序虚拟化
- C/C++中关于qsort的使用
- How to show only next line after the matched one?
- 云服务器部署项目:vue-cli 部署服务配置
- java认证考试试卷_java认证考试试题及答案
- 怎么用虚拟机搭建云服务器,利用虚拟机搭建云服务器
- 文件或目录损坏且无法读取
- xp系统工作组计算机没有权限访问权限,XP系统工作组计算机没有法访问如何处理?...
- 大师速写作品及理论,有你喜欢的知识
- java.net.MalformedURLException: unknown protocol: jrt 异常解决方法
- 【C++】VAL树的旋转(左单旋、右单旋、双旋)
- python-turtle(海龟绘图)圣诞树
- PTA python 求分数序列前N项和