拉格朗日乘数法和KKT条件的直观解释

标签（空格分隔）：机器学习

linbin 2018-05-10

Abstract

在SVM的推导中，最优化问题是其中的核心，这里我们简单介绍下最优化问题，特别是带有约束的最优化问题，并且引入拉格朗日乘数法和广义拉格朗日乘数法，介绍并且直观解释了KKT条件，用于解决带约束的最优化问题。

最优化问题

我们在高中，包括在高数中都会经常遇到求解一个函数的最小值，最大值之类的问题，这类问题就是属于最优化问题。比如给出下列一个不带有约束的最优化问题：
(1.1)
其中的

3x2+4x+5 3 x 2 + 4 x + 5

3{x^2}+4x+5我们称为目标函数(objective function)。这样的问题，直接利用罗尔定理（Rolle’s theorem）求出其鞍点，又因为其为凸函数而且可行域是整个R，求出的鞍点便是最值点，这个是对于无约束最优化问题的解题套路。
如果问题带有约束条件，那么就变得不一样了，如：
(1.2)

因为此时的约束条件是仿射函数（affine function），所以可以利用换元法将x表示为y的函数，从而将目标函数变为无约束的形式，然后利用罗尔定理便可以求出最值点了。
然而如果约束条件一般化为g(x,y)=c，那么x就不一定可以用其他变量表示出来了，这个时候就要利用拉格朗日乘数法(Lagrange multipliers )了。

拉格朗日乘数法(Lagrange multipliers)

我们先一般化一个二元最优化问题为(2.1)形式：

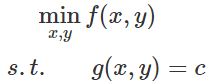(2.1)

将目标函数f(x,y)和等式约束条件g(x,y)=c画出来就如下图所示：

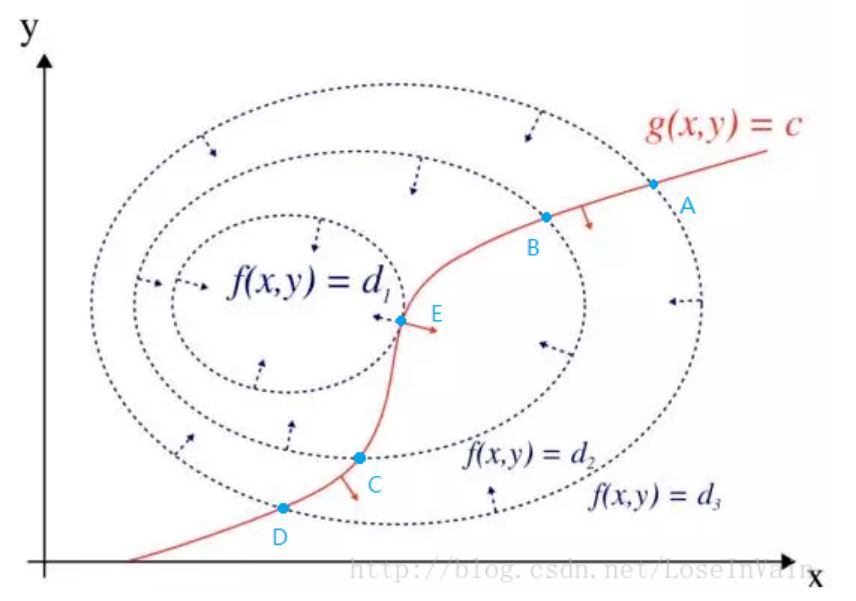
其中的f(x,y)虚线为等高线，而红线为g(x,y)=c这个约束函数曲线与f(x,y)的交点的连线在x−y平面的映射。其中，假设有d₃>d₂>d₁， d1点为最小值点（最优值点）。从直观上可以发现，在g(x,y)=c与f(x,y)的非最优化交点A,B,C,D上，其f(x,y)和g(x,y)的法线方向并不是共线的，注意，这个相当关键，因为如果不是共线的，说明g(x,y)=c与f(x,y)的交点中，还存在可以取得更小值的点存在。对于A点来说，B点就是更为小的存在。因此，我们从直觉上推论出只有当g(x,y)=c与f(x,y)的法线共线时，才是最小值点的候选点（鞍点）。推论到多元变量的问题的时候，法线便用梯度表示。于是，我们有原问题取得最优值的必要条件：

(2.2)其中的λ表示两个梯度共线。
可以简单的变形为

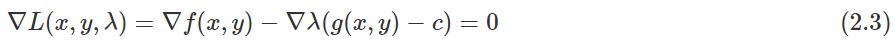
让我们去掉梯度算子，得出

这个时候λ取个负号也是不影响的，所以式子(2.4)通常写作：

看！我们得出了我们高数中经常见到的等式约束下的拉格朗日乘数函数的表示方法。

多约束的拉格朗日乘数法

以上，我们讨论的都是单约束的拉格朗日乘数法，当存在多个等式约束时（其实不等式约束也是一样的），我们进行一些推广。先一般化一个二元多约束最小化问题：

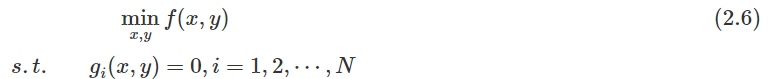
对于每个目标函数和约束配对，我们有:

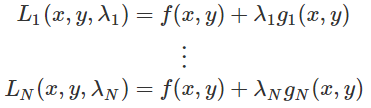
将上式相加有：

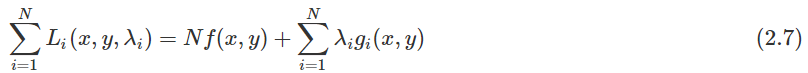
定义多约束的拉格朗日函数为：

因为λ_i是常数，表示共线的含义而已，所以乘上一个常数

1N 1 N

\frac 1N也不会有任何影响，我们仍然用λ _i表示，因此式子(2.8)变成：

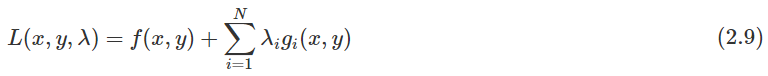
这就是多约束拉格朗日乘数法的函数表达形式。

一个计算例子

让我们举一个单约束的拉格朗日乘数法的计算例子，例子来源于引用3。
给出一个最大化任务：

图像如：

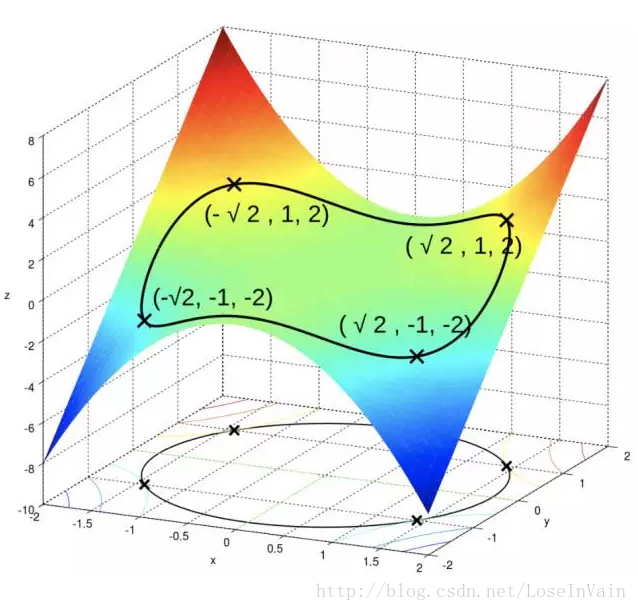
广义拉格朗日乘数法(Generalized Lagrange multipliers)

为了接下来的讨论方便，我们将N设为3，并且去掉等式约束，这样我们的最小化问题的广义拉格朗日函数就变成了：

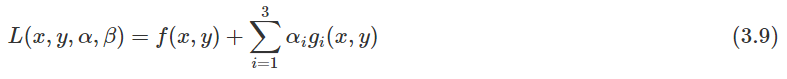
绘制出来的示意图如下所示：

引用

拉格朗日乘子法如何理解？知乎
《统计学习方法》豆瓣
《【直观详解】拉格朗日乘法和KKT条件》微信公众号
《解密SVM系列（一）：关于拉格朗日乘子法和KKT条件》 CSDN
Karush–Kuhn–Tucker conditions wikipedia
拉格朗日乘数法和KKT条件的直观解释