本人的LeetCode账号：魔术师的徒弟，欢迎关注获取每日一题题解，快来一起刷题呀~
本人Gitee账号：路由器，欢迎关注获取博客内容源码。
文章目录
- 一、知识框架
- 二、质数
- - 1、质数的判定—试除法
  - 2、分解质因数—试除法
  - 3、筛质数
  - - 1 朴素筛法
    - 2 优化1—埃氏筛法
    - 3 优化2—线性筛法
    - 4 leetcode204. 计数质数
- 三、约数
- - 1、试除法求约数
  - 2、约数个数与约数之和
  - 3、最大公约数—欧几里得算法
- 四、欧拉函数
- - 1 公式法求欧拉函数
  - 2 筛法求欧拉函数
  - 3 Acwing201.可见的点
  - 4 数论中的欧拉定理
- 五、快速幂算法
- - 1 模板题
  - 2 快速幂求模n(n是质数)意义下的逆元
- 六、扩展欧几里得算法
- - 1 裴蜀定理
  - 2 求解线性同余方程
- 七、中国剩余定理
- - 1 中国剩余定理
  - 2 模板题

一、知识框架

数论
组合计数
高斯消元
简单博弈论

本篇有关内容是数论有关的内容。

二、质数

质数是针对所有大于1的自然数定义的，如果它的约数只有1和它本身，那么这个数就是一个质数（素数）。

1、质数的判定—试除法

原始版本：

bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i < x; ++i){if (x % i == 0) return false;}return true;
}

这是一个O(n)的算法，我们可以这样优化，定义d | n表示d能整除n(如3能整除12)，有如下性质：
d∣n−>nd∣nd | n->\frac{n}{d} | n d∣n−>dn∣n
因为n的所有约数都是成对出现的，所以我们只要枚举所有小的数，就会通过这个转化枚举完大的数，即d <= n / d的数即可。

bool is_prime(int x)
{if (x < 2) return false;for (int i = 2; i <= x / i; ++i)// 不推荐 i <= sqrt(x) sqrt比较慢// 不推荐 i * i <= x i * i存在溢出风险// 推荐写法 i <= x / i{if (x % i == 0) return false;}return true;
}

时间复杂度：O(sqrt(n))。

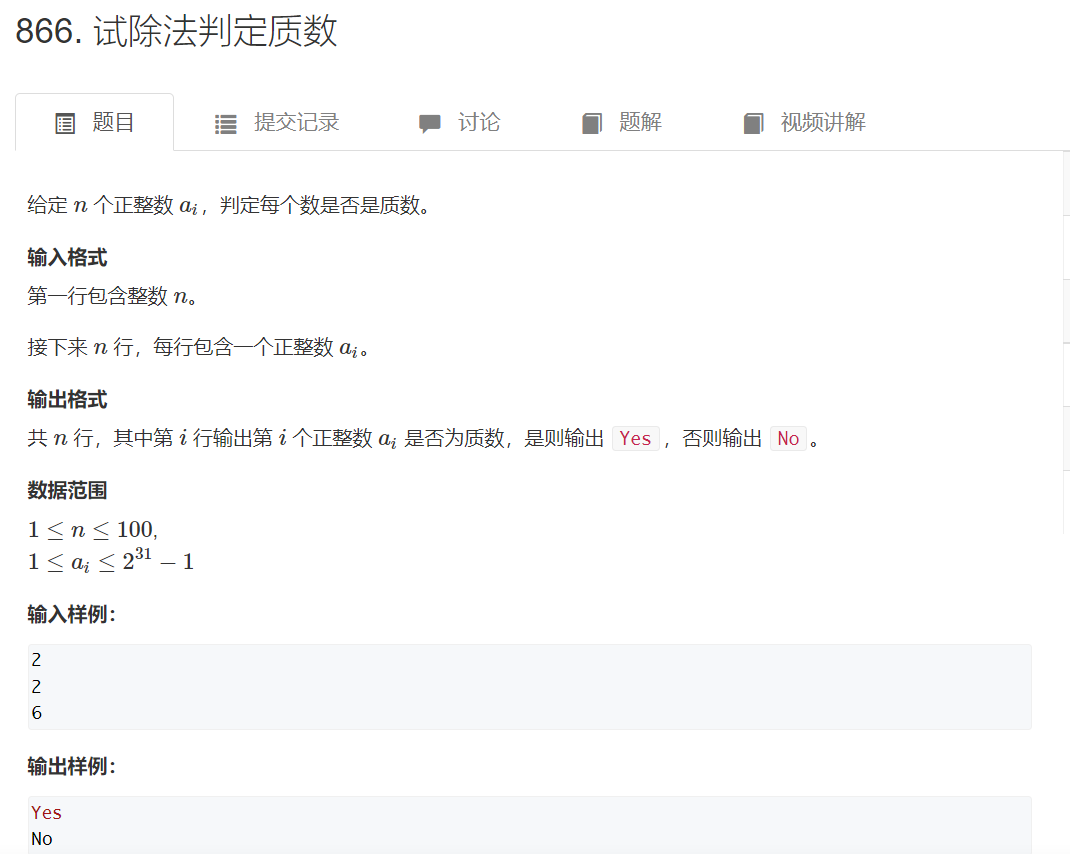
题解：

#include <iostream>
using namespace std;bool isPrime(int n)
{if (n < 2) return false;for (int i = 2; i <= n / i; ++i){if (n % i == 0) return false;}return true;
}int main()
{int n, x;cin >> n;while (n--){cin >> x;if (isPrime(x)) puts("Yes");else puts("No");}return 0;
}

2、分解质因数—试除法

n=p1k1∗...∗pmkmn = p_{1}^{k_{1}}*...*p_{m}^{k_m} n=p1k1∗...∗pmkm

基本思路：从小到达枚举n的所有数i，如果i | n，则定义s = 0，然后让n去把其次数除尽。

void divide(int n)
{for (int i = 2; i <= n; ++i){// 因为 n /= i，所以当我们枚举到i时，// 已经把所有2 ~ i - 1的质因子都除干净了// n中不包含任何2 ~ i - 1的质因子了// 而 n % i == 0 因此i也不包含任何 2 ~ i - 1的质因子。// 因此此时i一定是质数。if (n % i == 0){int s = 0;while (n % i == 0){s++;n /= i;}// 打印这个因子的次数printf("%d %d\n", i, s);}}
}

现在我们的时间复杂度是O(n)，对应n是质数的情况。

优化：注意到一个性质：n中最多只有一个大于sqrt(n)的质因子，证明就是考虑如果有两个大于sqrt(n)的质因子，那么它们乘在一起一定会大于n。

所以我们可以先把小于sqrt(n)的质因子枚举出来：i <= n / i。如果最后n还大于1，那么这是的n就是剩下的那个大于sqrt(n)的质因子，单独提出即可if (n > 1) printf("%d %d\n", n, 1);。

#include <iostream>
using namespace std;void divide(int n)
{for (int i = 2; i <= n / i; ++i){if (n % i == 0){int cnt = 0;while (n % i == 0){++cnt;n /= i;}printf("%d %d\n", i, cnt);}}// 如果n > 1 那么它就是剩下的那个大于sqrt(n)的质因子if (n > 1) printf("%d %d\n", n, 1);
}int main()
{int n;cin >> n;int x;while (n--){cin >> x;divide(x);cout << endl;}return 0;
}

时间复杂度：O(sqrt(n))。

3、筛质数

1 朴素筛法

朴素做法的原理就是把从2开始，把所有自己的倍数都筛掉，从头往后晒，最后剩下的数就是质数。

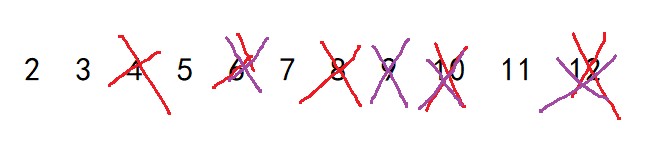
它的原理如下：p没被筛掉，说明2_{p-1的任何一个数都没有把p筛掉，即2}p-1的任何一个数都不是p的因子，所以p是素数。

int getprime(int n)
{for (int i = 2; i <= n; ++i){// 如果没被筛过 它就是素数if (!st[i]) prime[sz++] = i;// 然后把它的倍数筛掉for (int j = i; j <= n; j += i) st[j] = true;}return sz;
}

时间复杂度分析：
2循环次数为n2,3循环次数为n3,...,总循环次数为n(12+13+...)n−>∞时，调和级数等于ln(n)+c,c是欧拉常数所以时间复杂度大概是nln(n)，又ln(n)<log2n,所以时间复杂度可以记为nlogn2循环次数为\frac{n}{2},3循环次数为\frac{n}{3},...,\\ 总循环次数为n(\frac{1}{2} + \frac{1}{3}+...)\\ n->∞时，调和级数等于ln(n) + c,c是欧拉常数\\ 所以时间复杂度大概是nln(n)，又ln(n) < log_2n,所以时间复杂度可以记为nlogn 2循环次数为2n,3循环次数为3n,...,总循环次数为n(21+31+...)n−>∞时，调和级数等于ln(n)+c,c是欧拉常数所以时间复杂度大概是nln(n)，又ln(n)<log2n,所以时间复杂度可以记为nlogn

2 优化1—埃氏筛法

一点点优化，我们其实没必要判断2~p - 1的所有数是否为p的因子，因为质数的性质，我们只要看看2~p - 1的所有质因子是否为p的因子就行了。

int getprime(int n)
{for (int i = 2; i <= n; ++i){// 如果没被筛过 它就是素数if (!st[i]) {// 把质数的倍数都删掉prime[sz++] = i;for (int j = i; j <= n; j += i) st[j] = true;}}return sz;
}

速度确实有提升。

时间复杂度分析：

我们现在只让让质数的倍数被筛掉了，所以这里调和级数就变成了质数为分子，根据质数定理，1~n大概有n / ln(n)个质数，所以本来我们要求和n个数，现在只需要求n / ln(n)个数，原时间复杂度nln(n),现在变成nln(n) / ln(n)，时间复杂度大概变成O(n)，但这只是一个估计，真实的时间复杂度是O(nloglogn)，调和级数中只算质数的话，求和大概是loglogn，这数很小，和O(n)大概是1个级别的。

3 优化2—线性筛法

思路也是把每个合数用它的质因子筛掉，但是想让每个合数只被筛一次。

它的核心是对任何一个合数n，它只会被它的最小质因子筛掉。

我们先上代码，再做讲解：

void getprime(int n)
{for (int i = 2; i <= n; ++i){if (!st[i]) Prime[sz++] = i;for (int j = 0; Prime[j] <= n / i; ++j){st[Prime[j] * i] = true;if (i % Prime[j] == 0) break;}}
}

1.当i%Pj==0时,Pj一定是i的最小质因数，那么它也一定是i∗Pj的最小质因子2.当i%Pj!=0时，Pj小于i的所有质因子，所以Pj也是Pj∗i的最小质因子综上，不论什么情况,Pj一定是Pj∗i的最小质因子对于一个合数x，假设Pj是x的最小质因子，当i枚举到x/Pj时，x就会被st[Pj∗i]给筛掉所以任何合数都会被它的最小质因子筛掉又因为每个数只有一个最小质因子，所以该算法时间复杂度是线性的。1.当i\%Pj==0时,Pj一定是i的最小质因数，那么它也一定是i * Pj的最小质因子\\ 2.当i\%Pj !=0时，Pj小于i的所有质因子，所以Pj也是Pj*i的最小质因子\\ 综上，不论什么情况,Pj一定是Pj*i的最小质因子\\ 对于一个合数x，假设Pj是x的最小质因子，当i枚举到x/Pj时，x就会被st[Pj * i]给筛掉\\ 所以任何合数都会被它的最小质因子筛掉\\ 又因为每个数只有一个最小质因子，所以该算法时间复杂度是线性的。 1.当i%Pj==0时,Pj一定是i的最小质因数，那么它也一定是i∗Pj的最小质因子2.当i%Pj!=0时，Pj小于i的所有质因子，所以Pj也是Pj∗i的最小质因子综上，不论什么情况,Pj一定是Pj∗i的最小质因子对于一个合数x，假设Pj是x的最小质因子，当i枚举到x/Pj时，x就会被st[Pj∗i]给筛掉所以任何合数都会被它的最小质因子筛掉又因为每个数只有一个最小质因子，所以该算法时间复杂度是线性的。

4 leetcode204. 计数质数

原题链接204. 计数质数

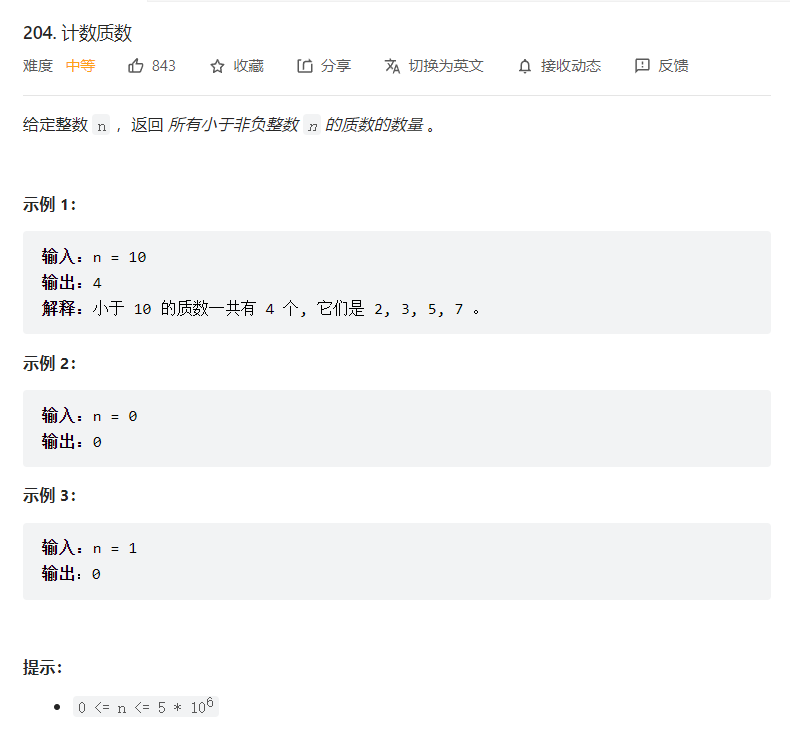
// 朴素筛法
class Solution {public:int countPrimes(int n) {int sz = 0;const int N = 5e6 + 10;int prime[N];vector<bool> st(n, false);for (int i = 2; i < n; ++i){if (!st[i]){prime[sz++] = i;}for (int j = i; j < n; j += i) st[j] = true;}return sz;}
};// 埃氏筛法
class Solution {public:int countPrimes(int n) {int sz = 0;const int N = 5e6 + 10;int prime[N];vector<bool> st(n, false);for (int i = 2; i < n; ++i){if (!st[i]){prime[sz++] = i;for (int j = i; j < n; j += i) st[j] = true;}}return sz;}
};//线性筛法
class Solution {public:int countPrimes(int n) {const int N = 5e6 + 10;bool st[N] = {0};int prime[N];int sz = 0;for (int i = 2; i < n; ++i){if (!st[i]) prime[sz++] = i;for (int j = 0; j < sz && prime[j] <= n / i; ++j){st[prime[j] * i] = true;if (i % prime[j] == 0) break;}}return sz;}
};

可以看出速度还是有所区别的。

三、约数

1、试除法求约数

一个数的约数也是成对出现的，所以求约数只要枚举比较小的约数就行了，另一个可以n / i自行求出。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;vector<int> get_divisors(int n)
{vector<int> res;for (int i = 1; i <= n / i; ++i){if (n % i == 0){res.push_back(i);// 防止重复if (n / i != i) res.push_back(n / i);}}sort(res.begin(), res.end());return res;
}int main()
{int cnt;cin >> cnt;int x;while (cnt--){cin >> x;vector<int> a = get_divisors(x);for (int t : a) cout << t << ' ';cout << endl;}return 0;
}

2、约数个数与约数之和

约数个数
根据算术基本定理:任何一个正整数N都可以表示为:N=p1a1∗....∗pkakN的任何一个约数d都可以表示为:d=N=p1b1∗....∗pkbk所以约数的个数可以根据乘法定理，个数为:(a1+1)(a2+1)∗...∗(ak+1)根据算术基本定理:\\ 任何一个正整数N都可以表示为:N=p_1^{a_{1}} * ....*p_k^{a_{k}}\\ N的任何一个约数d都可以表示为: d = N=p_1^{b_{1}} * ....*p_k^{b_{k}}\\ 所以约数的个数可以根据乘法定理，个数为:(a_1 + 1)(a_2 + 1)*...*(a_k + 1) 根据算术基本定理:任何一个正整数N都可以表示为:N=p1a1∗....∗pkakN的任何一个约数d都可以表示为:d=N=p1b1∗....∗pkbk所以约数的个数可以根据乘法定理，个数为:(a1+1)(a2+1)∗...∗(ak+1)
我们这样就把

int范围内，约数个数最多的一个数它的约数个数为1500个。

约数之和：

有了刚刚的分解，约数的和就是：
(p10+p11+...+p1a1)∗...∗(pk0+pk1+...+pkak)(p_1^0 + p_1^1 + ...+p_1^{a_1}) *...*(p_k^0 +p_k^1+ ...+p_k^{a_k}) (p10+p11+...+p1a1)∗...∗(pk0+pk1+...+pkak)
验证用乘法分配律展开即可。

思路就是分解乘积的质因数等于分解每个因子的质因数，然后累记一下，然后套公式就行了。

#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 1e9 + 7;
typedef unsigned long long ULL;int main()
{unordered_map<int, int> hash;// <pj, ai>int n;int x;cin >> n;while (n--){cin >> x;// 分解x的质因数for (int i = 2; i <= x / i; ++i){if (x % i == 0){while (x % i == 0){++hash[i];x /= i;}}}if (x > 1) ++hash[x];}ULL res = 1;for (auto p : hash) res = (res * (p.second + 1)) % N;cout << res << endl;return 0;
}

思路同上，分解每个因子的质因数后，套入约数之和的公式即可。

#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 1e9 + 7;
typedef unsigned long long ULL;int main()
{unordered_map<int, int> hash;// <pj, ai>int n;int x;cin >> n;while (n--){cin >> x;// 分解x的质因数for (int i = 2; i <= x / i; ++i){if (x % i == 0){while (x % i == 0){++hash[i];x /= i;}}}if (x > 1) ++hash[x];}ULL res = 1;for (auto p : hash){ULL sum = 0;ULL base = 1;for (int i = 0; i <= p.second; ++i){sum = (sum + base) % N;base = (base * p.first) % N;}res = (res * sum) % N;}cout << res << endl;return 0;
}

3、最大公约数—欧几里得算法

根本原理就是(a, b) = (b, a mod b)，证明来说就是左边的公约数集合等于右边的公约数集合。

#include <iostream>
using namespace std;int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}int main()
{int n;cin >> n;int a, b;while (n--){cin >> a >> b;cout << gcd(a, b) << endl;}return 0;
}

时间复杂度:O(logn)。

四、欧拉函数

什么是欧拉函数呢？
φ(n):1−n中与n互质的数的个数。φ(n):1-n中与n互质的数的个数。 φ(n):1−n中与n互质的数的个数。
互质指的是公约数只有1的一对自然数。

1 公式法求欧拉函数

关于欧拉函数，有如下定理：

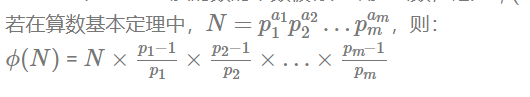
证明：

为了得到1~N中和N互质的数的个数，

先从1~N中去掉p1,p2,...pk的所有倍数，他们的个数是N/pi：

N−Np1−NP2−...−NpkN - \frac{N}{p_1} - \frac{N}{P_2}-...-\frac{N}{p_k} N−p1N−P2N−...−pkN

有的数既是pi的倍数，又是pj的倍数，这样被减了两次，再加回来：

N−Np1−NP2−...−Npk+Np1p2+Np1p3+...N - \frac{N}{p_1} - \frac{N}{P_2}-...-\frac{N}{p_k}+\frac{N}{p_1p_2} + \frac{N}{p_1p_3}+... N−p1N−P2N−...−pkN+p1p2N+p1p3N+...

有的数既是pi的倍数，又是pj的倍数，还是pk的倍数，它们会在上上一轮被减三次，在上一轮被加三次，但是实际上我们是要减去它们的，因此再减去所有pi*pj*pk的倍数：

N−Np1−NP2−...−Npk+Np1p2+Np1p3+...−Np1p2p3−....N - \frac{N}{p_1} - \frac{N}{P_2}-...-\frac{N}{p_k}+\frac{N}{p_1p_2} + \frac{N}{p_1p_3}+...-\frac{N}{p_1p_2p_3}-.... N−p1N−P2N−...−pkN+p1p2N+p1p3N+...−p1p2p3N−....

这样就找到了一个规律，后面再加上所有四个素数相乘，再减去所有五个素数相乘…。

发现把式子：
N(1−1p1)(1−1p2)....(1−1pk)N(1-\frac{1}{p_1})(1-\frac{1}{p_2})....(1-\frac{1}{p_k}) N(1−p11)(1−p21)....(1−pk1)
展开即为答案。

首先我们要获得每个数的质因数，前面一节学习过了，时间复杂度是sqrt(n)，然后套公式就可以获得每个数的欧拉函数。

#include <iostream>
using namespace std;int main()
{int n;cin >> n;int x;while (n--){cin >> x;int res = x;// 分解质因数的同时套用欧拉函数 // 为了不出现小数 每一项改为a / p * (p - 1)for (int i = 2; i <= x / i; ++i){if (x % i == 0){res = res / i * (i - 1);while (x % i == 0){x /= i;}}}if (x > 1) res = res / x * (x - 1);cout << res << endl;}return 0;
}

2 筛法求欧拉函数

我们在某些情况下需要求1-n每个数的欧拉函数，如果我们对每个数套一遍公式，那么时间复杂度会是O(n*sqrt(n))非常的慢，我们可以用筛法来获得欧拉函数，它的时间复杂度可以降低到O(n).

LL get_Eulers(int n)
{Euler[1] = 1;// 和1互质的数只有它自己 就1个for (int i = 2; i <= n; ++i){if (!st[i]){// 走到这里 i是质数 质数的欧拉函数就是i - 1// 1 ~ i - 1都是和它互质的数Euler[i] = i - 1;}for (int j = 0; primes[j] <= n / i; ++j){// 线性筛法中证明了 不论哪种情况 prime[j]是i * prime[j]的最小质因子st[primes[j] * i] = true;if (i % primes[j] == 0){// 走到这里 primes[j] * i的质因子和i的质因子一样// 那么他们的欧拉函数的差别就是一个primes[j]Euler[i * primes[j]] = Euler[i] * primes[j];break;}// 否则i中没有primes[j]这个质因子 差一个(primes[j] - 1) / primes[j] * primes[j]Euler[primes[j] * i] = Euler[i] * (primes[j] - 1);}}
}

模板题：

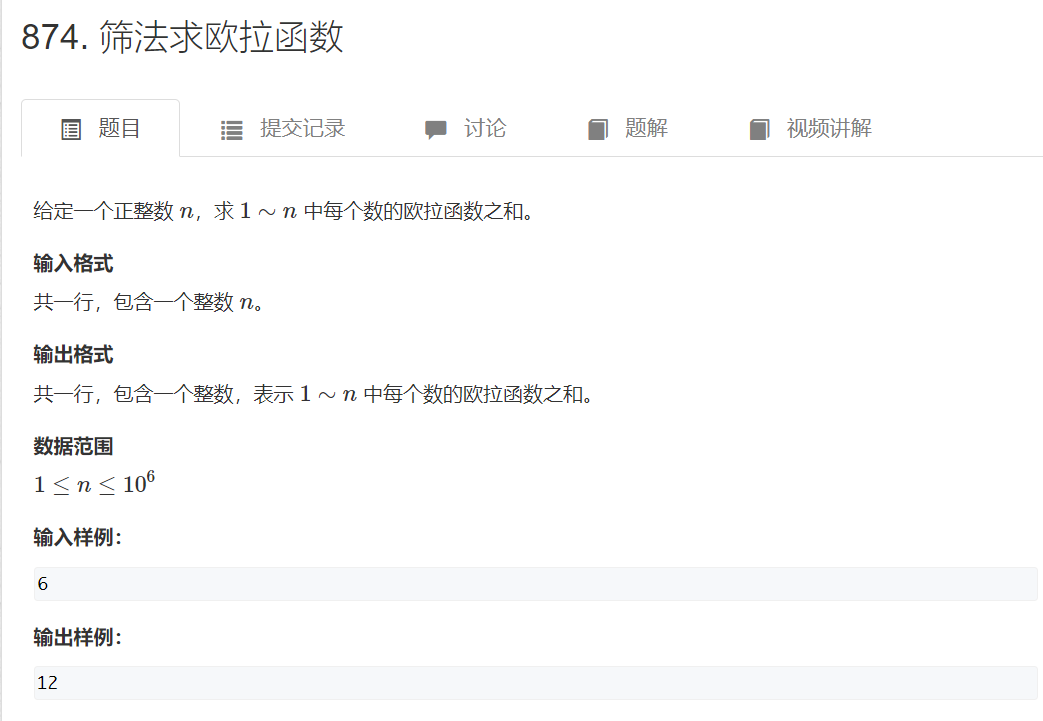
#include <iostream>
#include <numeric>
using namespace std;typedef long long LL;
const int N = 1e6 + 10;bool st[N];
int primes[N];
int sz = 0;
int Euler[N];LL get_Euler(int n)
{Euler[1] = 1;// 与1互质的数只有它自己// 走一个线性筛法for (int i = 2; i <= n; ++i){if (!st[i]){// 记录素数primes[sz++] = i;// i 是素数 它的欧拉函数等于i - 1Euler[i] = i - 1;}for (int j = 0; primes[j] <= n / i; ++j){st[primes[j] * i] = true;if (i % primes[j] == 0){// 到这里 首先primes[j]是i * primes[j]的最小质因数// 并且i中有primes[j]这个因子 // 所以primes[j] * i的欧拉函数仅仅比i的欧拉函数多一个primes[j]Euler[primes[j] * i] = Euler[i] * primes[j];break;}// 到这里 i中没有primes[j]的因子 但是primes[j]是i * primes[j]的最小质因子// 所以他俩的欧拉函数差了一个 primes[j] * (primes[j] - 1) / primes[j] = primes[j] - 1Euler[primes[j] * i] = Euler[i] * (primes[j] - 1);}}LL res = accumulate(Euler + 1, Euler + n + 1, (LL)0);return res;
}int main()
{int n;cin >> n;cout << get_Euler(n) << endl;return 0;
}

3 Acwing201.可见的点

意识到如果x和y都不等于0时，可见点的x和y一定是互质的，并且一对互质的(x, y)可以对应出两个点(对角线除外)，所以对每个数i : [1, n]，我们可以求出来1~i中所有与它互质的点的个数Euler(i)，这就相当于在第一象限的一半位置的某个x上计算可视的点，然后把他们求和再乘2，这里因为(1, 1)这个点在对角线上，所以它乘二后相当于除了计算了自己补上了一个坐标轴上的1个可视点，然后再+1就可以在补上另一个坐标轴上的可视点，这样就够了。

#include <iostream>
#include <numeric>
using namespace std;
typedef unsigned long long ULL;
const int N = 1010;
int primes[N];
int sz = 0;
bool st[N];
int Euler[N];void get_Euler(int n)
{Euler[1] = 1;for (int i = 2; i <= n; ++i){if (!st[i]){Euler[i] = i - 1;primes[sz++] = i;}for (int j = 0; primes[j] <= n / i; ++j){st[i * primes[j]] = true;if (i % primes[j] == 0){Euler[i * primes[j]] = Euler[i] * primes[j];break;}Euler[i * primes[j]] = Euler[i] * (primes[j] - 1);}}
}int main()
{get_Euler(N - 1);int cnt, n;cin >> cnt;for (int i = 1; i <= cnt; ++i){cin >> n;ULL res = accumulate(Euler + 1, Euler + n + 1, (ULL)0) * 2 + 1;printf("%d %d %llu\n", i, n, res);}return 0;
}

4 数论中的欧拉定理

若a与n互质，则
aφ(n)(mod)n==1a^{φ(n)}(mod)n == 1 aφ(n)(mod)n==1
证明：
假设1−n中，与n互质的数有：a1,a2,...,aφ(n)那么又因为a与n互质，所以a∗a1,a∗a2,...,a∗aφ(n)都与n互质有因为a与n互质，所以a∗a1,a∗a2,...,a∗aφ(n)在modn的意义下同余于a1,a2,...,aφ(n)左边就是aφ(n)∗a1∗a2∗...∗aφ(n)==a1∗a2∗...∗aφ(n)(mod..n)又因为a1∗a2∗...∗aφ(n)与n互质，所以左右两边消掉有：aφ(n)==1(mod..n)即aφ(n)(mod)n=1假设1-n中，与n互质的数有：a_1,a_2,...,a_{φ(n)}\\ 那么又因为a与n互质，所以a*a_1,a*a_2,...,a*a_{φ(n)}都与n互质\\ 有因为a与n互质，所以a*a_1,a*a_2,...,a*a_{φ(n)}在modn的意义下同余于a_1,a_2,...,a_{φ(n)}\\ 左边就是a^{φ(n)}*a_1*a_2*...*a_{φ(n)} == a_1*a_2*...*a_{φ(n)}(mod..n)\\ 又因为a_1*a_2*...*a_{φ(n)}与n互质，所以左右两边消掉有：\\ a^{φ(n)}==1(mod..n)\\ 即a^{φ(n)}(mod)n = 1 假设1−n中，与n互质的数有：a1,a2,...,aφ(n)那么又因为a与n互质，所以a∗a1,a∗a2,...,a∗aφ(n)都与n互质有因为a与n互质，所以a∗a1,a∗a2,...,a∗aφ(n)在modn的意义下同余于a1,a2,...,aφ(n)左边就是aφ(n)∗a1∗a2∗...∗aφ(n)==a1∗a2∗...∗aφ(n)(mod..n)又因为a1∗a2∗...∗aφ(n)与n互质，所以左右两边消掉有：aφ(n)==1(mod..n)即aφ(n)(mod)n=1
推论：若p是质数，且a和p互质，则
ap−1(mod)p=1a^{p - 1}(mod)p=1 ap−1(mod)p=1
此推论被称为费马小定理。

五、快速幂算法

1 模板题

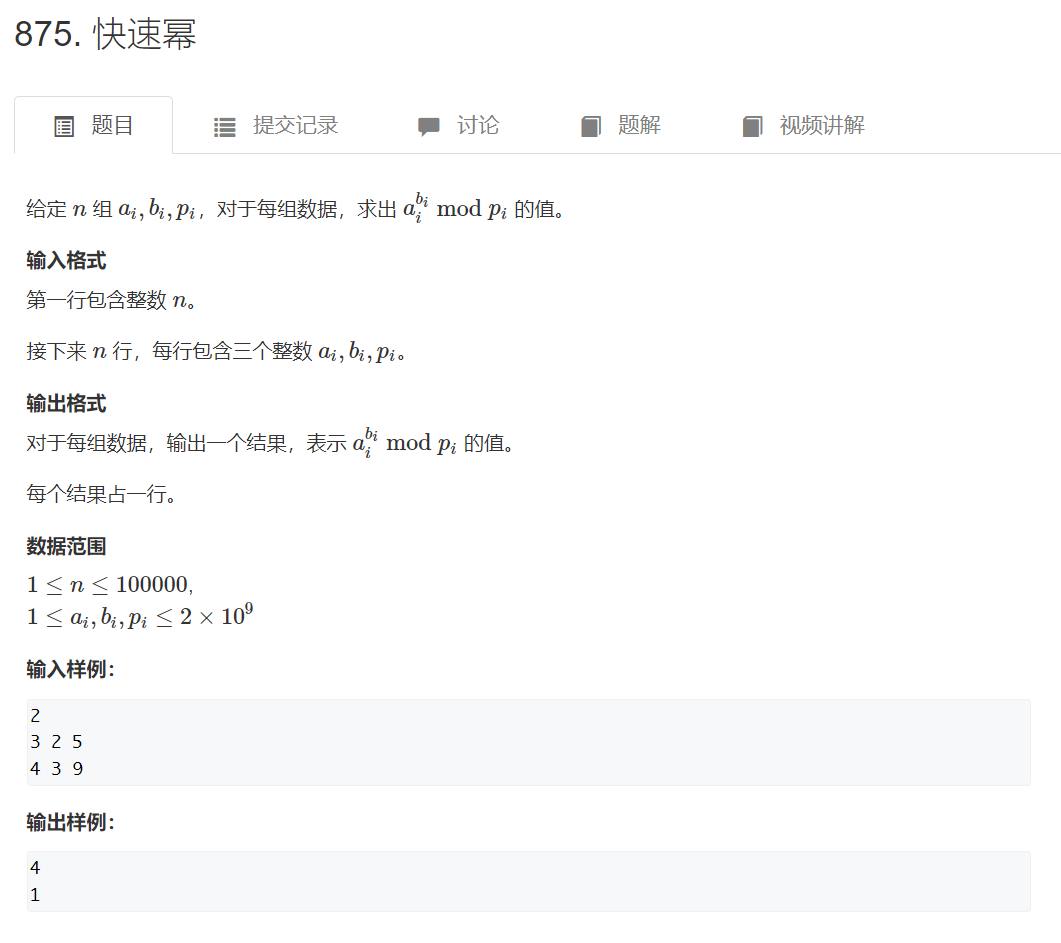
快速幂算法是快速的求出来a^k % p的结果，时间复杂度为O(logk),数据范围为1 <= a,p,k <= 1e9.

思路就是先预处理出一下内容，然后进行二进制位组合：

一个例子：

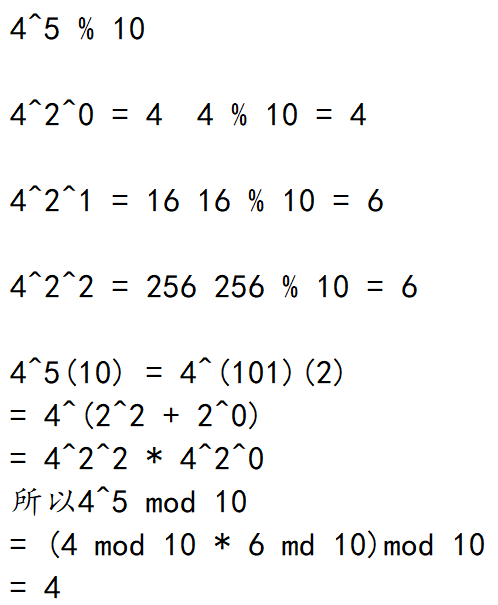
#include <iostream>
using namespace std;
typedef long long LL;int quick_power(int a, int b, int p)
{int res = 1;// 本质就是要求b的二进制表示while (b != 0){// 如果当前b的最低位为1 则让res和a乘一下 记得由于会爆int强转一下if (b & 1) res = (LL)res * a % p;b >>= 1;// a自己乘2 表示走到下一位a = (LL)a * a % p;}return res;
}int main()
{int n;scanf("%d", &n);int a, b, p;while (n--){scanf("%d%d%d", &a, &b, &p);int res = quick_power(a, b, p);printf("%d\n", res);}return 0;
}

之前我学习快速幂写出的方法：

#include <iostream>
using namespace std;
typedef unsigned long long LL;
int main()
{int n;scanf("%d", &n);LL base, power, p;while (n--){scanf("%ld%ld%ld", &base, &power, &p);LL res = 1;while (power > 0){if (power & 1){res = (res * base) % p;power--;}power >>= 1;base = (base * base) % p;}printf("%ld\n", res);}return 0;
}

测试来看，好像会更快一些：

2 快速幂求模n(n是质数)意义下的逆元

题目描述比较绕，实际上就是
假设b∣a,b与n互质a/b因为除法的运算比较麻烦，我们希望转而计算乘法做到(a/b)%n=(a∗x)%n找到这个xa/b==a∗b−1(mod(n))假设b|a,b与n互质\\ a/b因为除法的运算比较麻烦，我们希望转而计算乘法\\ 做到(a/b)\%n = (a * x) \%n\\ 找到这个x\\ a / b == a * b^{-1}(mod(n)) 假设b∣a,b与n互质a/b因为除法的运算比较麻烦，我们希望转而计算乘法做到(a/b)%n=(a∗x)%n找到这个xa/b==a∗b−1(mod(n))
性质：(两边同乘b就可以得证)
b∗b−1%n=1b*b^{-1}\%n = 1 b∗b−1%n=1
题目中假设了n = p是个质数，由费马小定理：
bp−1==1(mod(p))b∗bp−2==1(mod(p))b^{p - 1} ==1(mod(p))\\ b * b^{p - 2} == 1(mod(p)) bp−1==1(mod(p))b∗bp−2==1(mod(p))
所以逆元就是b^{p - 2}。

所以本题就是考察的a^{p - 2} % p，考察的就是一个快速幂算法。

一个例子a = 3，p = 5.
ap−2=33=27,27%5=2a−1=2(mod5)a ^ {p - 2} = 3 ^ 3 = 27,27\%5 = 2\\ a^{-1} = 2(mod5) ap−2=33=27,27%5=2a−1=2(mod5)
注意，当a和p不互质时，因为p是质数，所以a % p == 0时，对任何数x，a * x == 0(mod p)，所以肯定不存在逆元。注意检查边界即可。

#include <iostream>
using namespace std;typedef long long LL;int quick_power(int a, int b, int p)
{int res = 1;while (b > 0){if (b & 1){res = (LL)res * a % p;--b;}b >>= 1;a = (LL)a * a % p;}return res;
}int main()
{int n;scanf("%d", &n);int a, p;while (n--){scanf("%d%d", &a, &p);if (a % p) printf("%d\n", quick_power(a, p - 2, p));else puts("impossible");}return 0;
}

六、扩展欧几里得算法

1 裴蜀定理

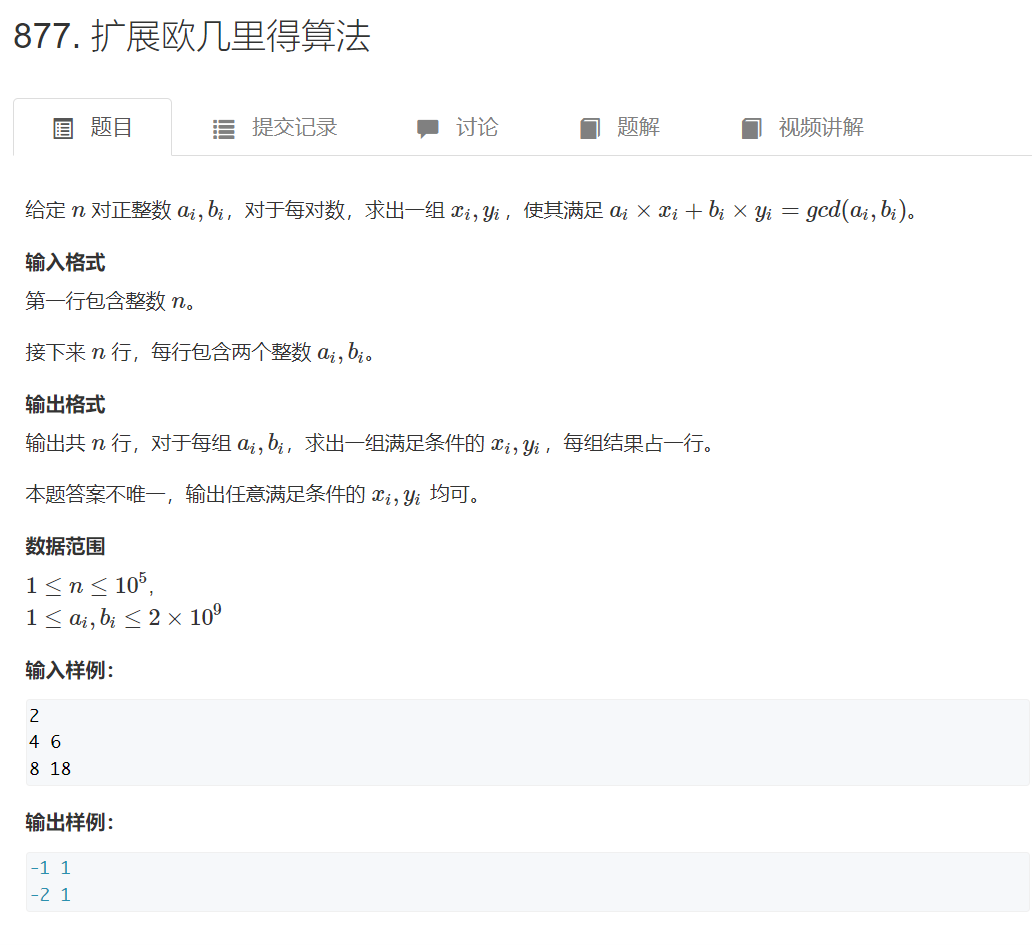
有一对正整数a，b，那么一定存在非0整数x，y，使得
ax+by=gcd(a,b)ax+by=gcd(a,b) ax+by=gcd(a,b)
证明：因为a是gcd(a, b)的倍数，b是gcd(a, b)的倍数，所以ax + by组合出来的数一定是gcd(a, b)的倍数。

只要证明出gcd(a, b)一定能被组合出来就行，这个组合构造的方法就是扩展欧几里得算法。

#include <iostream>
using namespace std;int exgcd(int a, int b, int& x, int& y)
{if (b == 0){x = 1, y = 0;return a;}// 递归时求得是b和a%b的系数 分别是y和x// 那么本来的系数x和y就可以整理得到：// by + (a%b)x = gcd(a, b)// by + (a - a / b * b)x = gcd(a, b)// ax + b(y - a / b * x) = gcd(a, b)//所以本来的x = x，y = y - a / b * xint d = exgcd(b, a % b, y, x);// x系数不变 y系数减少a / b * xy -= a / b * x;return d;
}int main()
{int n, a, b, x, y;scanf("%d", &n);while (n--){scanf("%d%d", &a, &b);exgcd(a, b, x, y);printf("%d %d\n", x, y);}return 0;
}

注意本解是不唯一的，当我们求出一组x0和y0时，就可以如下再构造出全部解：
a(x0−k∗bgcd(a,b))+b(y0+k∗agcd(a,b))=gcd(a,b),k属于Za(x_0 - k*\frac{b}{gcd(a, b)}) + b(y_0 + k*\frac{a}{gcd(a,b)}) = gcd(a, b),k属于Z a(x0−k∗gcd(a,b)b)+b(y0+k∗gcd(a,b)a)=gcd(a,b),k属于Z
全部解的证明思路如下：我们已经获得了特解，根据线性方程组的理论，接下来我们只要求出ax + by = 0的通解，就能得到原方程的通解。
ax+by=0的通解是x=−baK,y=K,K为任意整数为了让x和y一定是整数,令K=agcd(a,b)k则得到x=−bgcd(a,b)k,y=agcd(a,b)k所以原方程通解为：x=x0−k∗bgcd(a,b),y=y0+k∗agcd(a,b)ax+by=0的通解是\\ x = -\frac{b}{a}K,y = K,K为任意整数\\ 为了让x和y一定是整数,令K=\frac{a}{gcd(a, b)}k\\ 则得到x = -\frac{b}{gcd(a, b)}k,y=\frac{a}{gcd(a, b)}k\\ 所以原方程通解为：x = x_0 - k*\frac{b}{gcd(a, b)}, y = y_0 + k*\frac{a}{gcd(a,b)} ax+by=0的通解是x=−abK,y=K,K为任意整数为了让x和y一定是整数,令K=gcd(a,b)ak则得到x=−gcd(a,b)bk,y=gcd(a,b)ak所以原方程通解为：x=x0−k∗gcd(a,b)b,y=y0+k∗gcd(a,b)a

2 求解线性同余方程

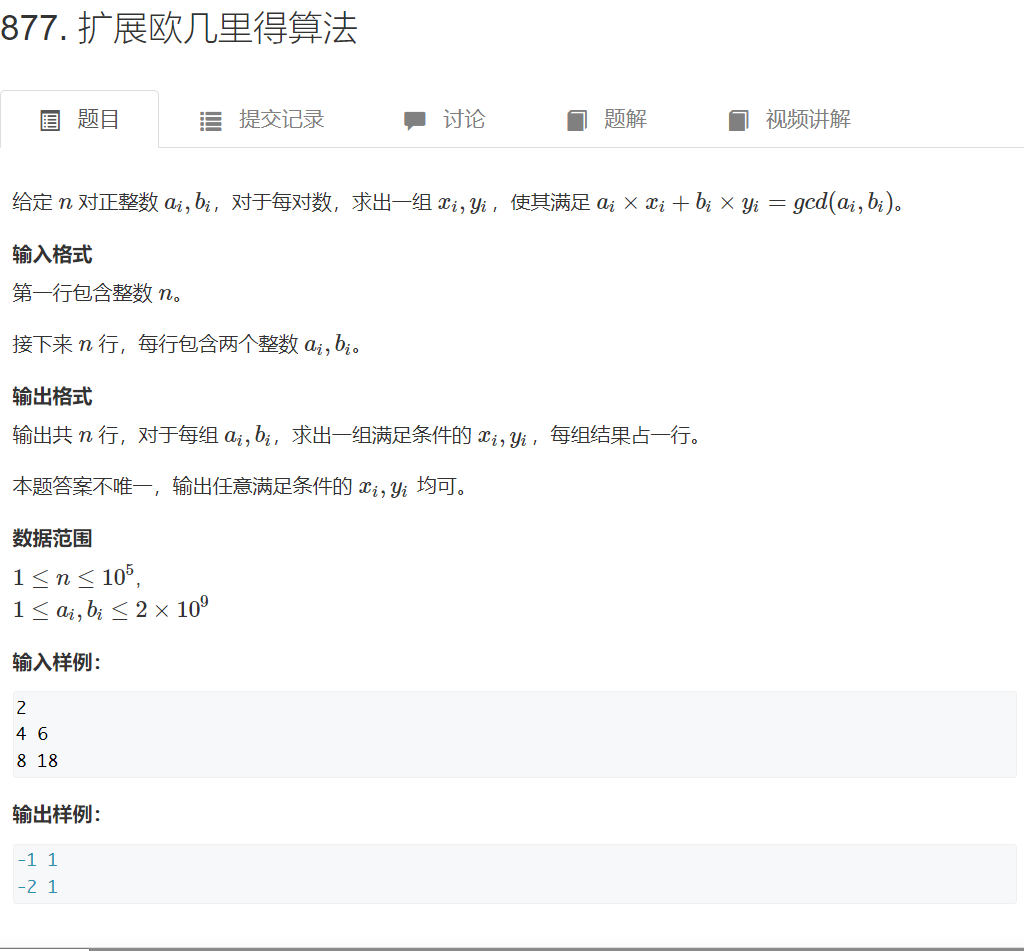
思路：

#include <iostream>
using namespace std;
typedef long long LL;int exgcd(int a, int b, int& x, int& y)
{if (b == 0){x = 1, y = 0;return a;}int d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}int main()
{int n, a, b, m, d, x, y;scanf("%d", &n);while (n--){scanf("%d%d%d", &a, &b, &m);d = exgcd(a, m, x, y);if (b % d == 0) printf("%d\n", (LL)x * b / d % m);else puts("impossible");}return 0;
}

七、中国剩余定理

1 中国剩余定理

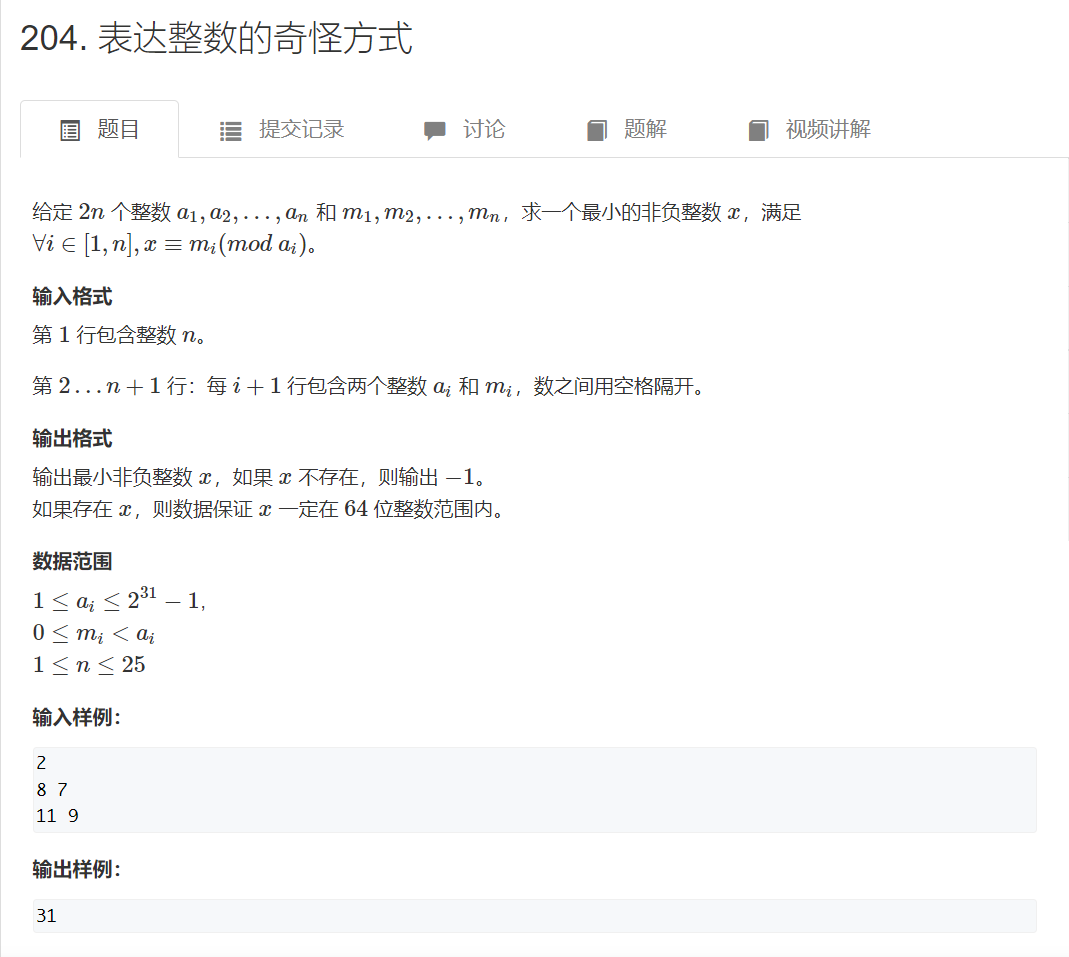
中国剩余定理的表述如下：

证明：

2 模板题

观察同余方程组中的两个方程:x%a1=m1x%a2=m2转化为:x=k1a1+m1x=k2a2+m2联立有:k1a1−k2a2=m2−m1它有解等价于m2−m1%gcd(a1,a2)==0假设得到了一组解k10,k20全部通解就是:k10+K∗a2gcd(a1,a2),k20+K∗a1gcd(a1,a2)代入原方程，得到x=k10a1+K∗[a1,a2]+m1=(m1+k10a1)+K∗[a1,a2]=x0+Ka这样就把两个方程化成了一个方程，这样n−1次就能把方程变成1个方程,在转化回同余方程:x==x0(mod(a)),就是求x0%a的正的余数就行.观察同余方程组中的两个方程:\\ x\%a_1=m_1\\ x\%a_2=m_2\\ 转化为:\\ x = k_1a_1 + m_1\\ x = k_2a_2 + m_2\\ 联立有:\\ k_1a_1-k_2a_2=m_2-m_1\\ 它有解等价于m_2 - m_1 \% gcd(a_1, a_2) == 0\\ 假设得到了一组解k_{10},k_{20}\\ 全部通解就是:k_{10} + K*\frac{a_2}{gcd(a_1,a_2)}, k_{20} + K*\frac{a_1}{gcd(a_1,a_2)}\\ 代入原方程，得到x=k_{10}a_1+K*[a_1,a_2]+m_1 = (m_1+k_{10}a_1) + K*[a_1,a_2]\\ =x_0+Ka\\ 这样就把两个方程化成了一个方程，这样n-1次就能把方程变成1个方程,在转化回同余方程:\\ x == x_0 (mod(a)),就是求x_0\%a的正的余数就行.\\ 观察同余方程组中的两个方程:x%a1=m1x%a2=m2转化为:x=k1a1+m1x=k2a2+m2联立有:k1a1−k2a2=m2−m1它有解等价于m2−m1%gcd(a1,a2)==0假设得到了一组解k10,k20全部通解就是:k10+K∗gcd(a1,a2)a2,k20+K∗gcd(a1,a2)a1代入原方程，得到x=k10a1+K∗[a1,a2]+m1=(m1+k10a1)+K∗[a1,a2]=x0+Ka这样就把两个方程化成了一个方程，这样n−1次就能把方程变成1个方程,在转化回同余方程:x==x0(mod(a)),就是求x0%a的正的余数就行.

#include <iostream>
using namespace std;
typedef long long LL;LL exgcd(LL a, LL b, LL& x, LL& y)
{if (b == 0){x = 1, y = 0;return a;}LL d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}int main()
{int n;cin >> n;LL a1, m1;// 先读入第一个方程的两个参数cin >> a1 >> m1;bool has_answer = true;for (int i = 0; i < n - 1; ++i){LL a2, m2;cin >> a2 >> m2;// 对方程 k1a1 - k2a2 = m2 - m1进行欧几里得算法LL k1, k2;LL d = exgcd(a1, a2, k1, k2);if ((m2 - m1) % d){has_answer = false;break;}//得到乘倍数得到解k1k1 *= (m2 - m1) / d;// 为了防止溢出 先把k1变到最小LL t = a2 / d;k1 = (k1 % t + t) % t;// 得到新方程的m1m1 = m1 + k1 * a1;// 得到新方程的a1 a1变成a1和a2的最小公倍数a1 = abs(a1 / d * a2);}if (has_answer){// 解一个方程x % a1 = m1的最小整数解 m1 % a1的整数解即可printf("%lld\n", (m1 % a1 + a1) % a1);}else puts("-1");return 0;
}

算法中的基础数学知识(一)—初等数论相关推荐

论文研读-多因子进化算法中的自适应知识迁移MFEA-AKT
论文研读-多因子进化算法中的自适应知识迁移MFEA-AKT Toward Adaptive Knowledge Transfer in Multifactorial Evolutionary Comp ...
VSLAM算法中的数学基础知识详细了解
学习SLAM经验告诉我,入门SLAM一般只需要两种两个方面的条件,一是要有扎实的数学基础,二是要有强大的动手编程能力,但是这两个条件对于刚入门的同学来说,极具挑战性. 学习SLAM的心里历程:本来先研 ...
算法中的数学基础知识
在开始讲算法前,先说说数学知识,数学是基础. 可以理解成计算机是数学的一个发展应用方向.闲话少说咱们开始. 1.求和公式及性质前n项和 a1+a2+a3+a4+-+an用下面方式表示初中学过前n项 ...
机器学习算法_机器学习算法中分类知识总结！
↑↑↑关注后"星标"Datawhale每日干货 & 每月组队学习,不错过Datawhale干货译者:张峰,Datawhale成员本文将介绍机器学习算法中非常重要的知识- ...
【机器学习基础】机器学习算法中分类知识总结！
译者:张峰,Datawhale成员本文将介绍机器学习算法中非常重要的知识-分类(classification),即找一个函数判断输入数据所属的类别,可以是二类别问题(是/不是),也可以是多类别问题( ...
数学/物理知识在软件/算法中应用(1)，数学知识应用
> 数学知识 1.拉普拉斯算子可以给图像锐化:2.傅里叶变化可以给图像去燥啊,压缩啊,提取特征那些吧. 3.高斯模糊:4.RSA,大数难分解:5.了解矩阵,Android开发之图像处理那点事-- ...
在遗传算法中出现等式约束_排序算法中的稳定性-等式的处理
在遗传算法中出现等式约束 by Onel Harrison 通过Onel Harrison 排序算法中的稳定性-等式的处理 (Stability in Sorting Algorithms - A T ...
std中稳定排序算法_敏哥：深挖亚马逊A9算法中的广告搜索排序
大家好,我是敏哥.最近国外疫情肆虐,牵动着所有跨境电商人的心.今天美国的确诊人数已经突破了33万人,每天以3万左右的确诊数量在增加,就连老虎也未能幸免. 国外疫情肆虐,对于跨境电商人而言并不是一个很好 ...
STL算法中函数对象和谓词
算法中函数对象和谓词函数对象和谓词定义函数对象谓词一元函数对象案例一元谓词案例二元函数对象案例二元谓词案例预定义函数对象和函数适配器使用预定义函数对象算术函数对象关系函数对象逻 ...

算法中的基础数学知识(一)—初等数论

文章目录