【数学与算法】牛顿法的两种应用：求根和最优化

原文链接：点击

平时总看到牛顿法怎样怎样，一直不得要领，今天下午查了一下维基百科，写写我的认识，很多地方是直观理解，并没有严谨的证明。在我看来，牛顿法至少有两个应用方向，1、求方程的根，2、最优化。牛顿法涉及到方程求导，下面的讨论均是在连续可微的前提下讨论。

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0x_0x0处展开，且展开到一阶，即:f(x)=f(x0)+(x－x0)f′(x0)f(x) = f(x_0)+(x－x_0)f'(x_0)f(x)=f(x0)+(x－x0)f′(x0)
求解方程f(x)=0f(x)=0f(x)=0，即f(x0)+(x−x0)∗f′(x0)=0f(x_0)+(x-x_0)*f'(x_0)=0f(x0)+(x−x0)∗f′(x0)=0 求解上式得到
x=x1=x0－f(x0)f′(x0)x =x_1=x_0－\frac{f(x_0)}{f'(x_0)}x=x1=x0－f′(x0)f(x0)
可以令x=x1x=x_1x=x1(这是为了我们使用迭代法求解)，得到
x1=x0－f(x0)f′(x0)\color{blue}x_1=x_0－\frac{f(x_0)}{f'(x_0)}x1=x0－f′(x0)f(x0)
因为这是利用泰勒公式的一阶展开，f(x)=f(x0)+(x－x0)f′(x0)f(x) = f(x_0)+(x－x_0)f'(x_0)f(x)=f(x0)+(x－x0)f′(x0)和原始的f(x)f(x)f(x)并不是完全相等，而是近似相等，这里求得的x1x_1x1并不能让f(x)=0f(x)=0f(x)=0，只能说f(x1)f(x_1)f(x1)的值比f(x0)f(x_0)f(x0)更接近f(x)=0f(x)=0f(x)=0。
于是乎，迭代求解的想法就很自然了，进而推出第n+1次迭代公式：
xn+1=xn－f(xn)f′(xn)\color{blue}x_{n+1}=x_n－\frac{f(x_n)}{f'(x_n)}xn+1=xn－f′(xn)f(xn)
通过迭代，这个式子必然在f(x∗)=0f(x^*)=0f(x∗)=0的时候收敛。

整个过程如下图：

2、牛顿法用于最优化

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

这个式子是成立的，当且仅当 Δx 无线趋近于0。此时上式等价与：

求解：

得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

其中H是hessian矩阵，定义为：

高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

1、牛顿法应用范围

牛顿法主要有两个应用方向：1、目标函数最优化求解。例：已知 f(x)的表达形式， $g(x)=\min\left\|{f(x)}\right\|$ ，求 $ming(x)$ ，及g(x)取最小值时的 x ?，即

由于||f(x)||通常为误差的二范数，此时这个模型也称为最小二乘模型，即 $\min\{{f^2}(x)\}$ 。

2、方程的求解（根）。例：求方程的解：g(x) = 0，求 x ？

这两个应用方面都主要是针对g(x)为非线性函数的情况。2中，如果g(x)为线性情况下的求解通常使用最小二乘法求解。

牛顿法的核心思想是对函数进行泰勒展开。

           2、牛顿法用于方程求解

对f(x)进行一阶泰勒公式展开：

$g(x){\approx}g({x_k})+g'({x_k})(x-{x_k})$    $(1)$

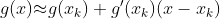
此时，将非线性方程 g(x) = 0 近似为线性方程：

$g({x_k})+g'({x_k})(x-{x_k})=0$    $(2)$

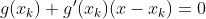
若 f’(x) != 0，则下一次迭代解为：

${x_{k+1}}={x_k}-\frac{1}{{g'({x_k})}}g({x_k})$       $(3)$

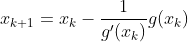
牛顿迭代示意图（因此Newton迭代法也称为切线法）：

3、牛顿法用于函数最优化求解

对f(x)进行二阶泰勒公式展开：

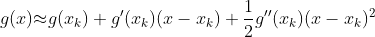
$g(x){\approx}g({x_k})+g'({x_k})(x-{x_k})+\frac{1}{2}g''({x_k}){(x-{x_k})^2}$     $(4)$

此时，将非线性优化问题 min f(x) 近似为为二次函数的最优化求解问题：

$\min\{g({x_k})+g'({x_k})(x-{x_k})+\frac{1}{2}g''({x_k}){(x-{x_k})^2}\}$     $(5)$

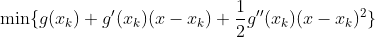
对于（5）式的求解，即二次函数（抛物线函数）求最小值，对（5）式中的函数求导：

$g'({x_k})+g''({x_k})(x-{x_k})=0$     $(6)$

$\Rightarrow{x_{k+1}}={x_k}-\frac{1}{{g''({x_k})}}g'({x_k})$    $(7)$

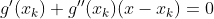
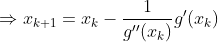
从本质上来讲，最优化求解问题的迭代形式都是： ${x_{k+1}}={x_k}-kg'({x_k})$ ，

其中k为系数， $g'({x_k})$ 为函数的梯度（即函数值上升的方向），那么 $-g'({x_k})$ 为下降的方向，

最优化问题的标准形式是：求目标函数最小值，只要每次迭代沿着下降的方向迭代那么将逐渐达到最优，

而牛顿将每次迭代的步长定为： $1/g''({x_k})$ 。

4、补充

a、严格来讲，在“3、牛顿法用于函数最优化求解”中对函数二阶泰勒公式展开求最优值的方法称为：Newton法，

而在“2、牛顿法用于方程求解”中对函数一阶泰勒展开求零点的方法称为：Guass-Newton（高斯牛顿）法。

b、在上面的陈述中，如果x是一个向量，那么公式中：

$g'({x_k})(x-{x_k})$ 应该写成： $g'{({x_k})^T}(x-{x_k})$ ， $g'({x_k})$ 为Jacobi(雅克比)矩阵。

$g''({x_k})(x-{x_k})$ 应该写成： ${(x-{x_k})^T}g''({x_k})(x-{x_k})$ ， $g''(x-{x_k})$ 为Hessian（海森）矩阵。

c、牛顿法的优点是收敛速度快，缺点是在用牛顿法进行最优化求解的时候需要求解Hessian矩阵。

因此，如果在目标函数的梯度和Hessian矩阵比较好求的时候应使用Newton法。

牛顿法在进行编程实现的时候有可能会失败，具体原因及解决方法见《最优化方法》-张薇东北大学出版社第155页。

5、Newton法与Guass-Newton法之间的联系

                        对于优化问题 $\min\left\|{f(x)}\right\|$ ，即 $\min\{{f^2}(x)\}$ ，当理论最优值为0时候，这个优化问题就变为了函数求解问题：

                                                              $\min\{{f^2}(x)\}{\Rightarrow}{f^2}(x)=0{\Rightarrow}f(x)=0$

                          结论：当最优化问题的理论最小值为0时，Newton法求解就可变为Guass-Newton法求解。

另外：对f(x)进行二阶泰勒展开：

f(x)=f(xk)+Jxk+0.5xk′Hxkf(x)=f({x_k})+J{x_k}+0.5{x_k'}H{x_k}f(x)=f(xk)+Jxk+0.5xk′Hxk

f(x)乘以f(x)的转置并忽略二次以上的项：

fT(x)f(x)={fT(xk)+(Jxk)T+(0.5xk′Hxk)T{f^T}(x)f(x)=\{{f^T}({x_k})+{(J{x_k})^T}+{(0.5{x_k'}H{x_k})^T}fT(x)f(x)={fT(xk)+(Jxk)T+(0.5xk′Hxk)T

∗{f(xk)+Jxk+0.5xk′Hxk}*\{f({x_k})+J{x_k}+0.5{x_k'}H{x_k}\}∗{f(xk)+Jxk+0.5xk′Hxk}

${\rm{=}}{f^T}({x_k})f({x_k})+2f({x_k})J{x_k}+x_k^T{J^T}J{x_k}+f({x_k})x_k^TH{x_k}$

$={f^T}({x_k})f({x_k})+2f({x_k})J{x_k}+x_k^T({J^T}J+f({x_k})H){x_k}$

因此，当xkx_kxk在最优解附近时，即满足f(xk)f(x_k)f(xk)，此时可认为：H=JTJH=J^TJH=JTJ

6、扩展阅读

a、修正牛顿(Newton)法

b、共轭方向法与共轭梯度法

c、拟牛顿法（避免求解Hessian矩阵）：DFP算法、BFGS算法

【数学与算法】牛顿法的两种应用：求根和最优化相关推荐

水平集方法引入主动轮廓模型算法中的两种方法
水平集方法引入主动轮廓模型算法中的两种方法 1.传统的基于主动轮廓模型和水平集理论的方法 2.变分水平集方法在讲解水平集理论在主动轮廓模型中的应用前,我们先用流程图说明一下常见的处理主动轮廓模型的流 ...
Java练习：两种方式求1+1/2!+1/3!+1/4!+...前20项的和、用for,while,do-while分别实现1+1/2!+1/3!+1/4!+...前20项的和
Java两种方式求 1+1/2!+1/3!+1/4!+... 前20项的和: 感叹号 !是阶乘的意思,如 2! .3! .4! 分别是:1*2 . 1*2*3 .1*2*3*4 第一种算法,如下代码 ...
Python两种方式求多个数的最大公因数（HCF）和最小公倍数（LCM）
Python两种方式求多个数的最大公因数(HCF)和最小公倍数(LCM) 最大公因数 1. 列表排序 2. 将列表分为两部分 3. 求最大公因数的质因子 4. 得到结果 5. 完整程序最小公倍数另 ...
数学-矩阵计算（4）两种布局
之前会发现在有的求导上最后结果需要转置,而有的不需要,很困惑,然后才发现了这个维基上面的解释(这才是写该博文的主要价值,注意到不同的布局问题,其他部分只是为了完整性而写的),而且下面也有很多很不错的参 ...
sum 去重_总结leetcode上【排列问题】【组合问题】【子集问题】回溯算法去重的两种写法！...
本周小结!(回溯算法系列三)续集在本周小结!(回溯算法系列三) 中一位录友对整颗树的本层和同一节点的本层有疑问,也让我重新思考了一下,发现这里确实有问题,所以专门写一篇来纠正,感谢录友们的积极交 ...
【CV/Matlab系列】基于Matlab的白平衡算法实现（两种方法）
DATE: 2020.11.22 文章目录 1.前言 2.白平衡算法 2.1 原始图像 2.2 灰色世界法 2.3 完美反射算法 1.前言在之前大学毕设时,设计了一种基于Matlab的白平衡算法,采 ...
PCA（2）：PCA算法实现的两种方式
因为样本个数和特征维度的是不相等de,所以组成的矩阵不是方阵. 第一种方式:特征分解思路(特征值分解要求分解的矩阵是方阵) 基于样本特征维度,先求协方差矩阵---->再特征分解(因为协方差矩阵是 ...
经典算法之基数排序两种实现
/************************ author's email:wardseptember@gmail.com date:2017.12.7 基数排序两种实现方法 ********* ...
417，BFS和DFS两种方式求岛屿的最大面积
想了解更多数据结构以及算法题,可以关注微信公众号"数据结构和算法",每天一题为你精彩解答.也可以扫描下面的二维码关注给定一个包含了一些0和1的非空二维数组grid . 一个岛屿是 ...
牛客 Tree(最小深度总和)（两种方法求重心）难度⭐⭐⭐
题目链接牛妹有一张连通图,由n个点和n-1条边构成,也就是说这是一棵树,牛妹可以任意选择一个点为根,根的深度deprootdep_{root}deproot为0,对于任意一个非根的点,我们将他到 ...

【数学与算法】牛顿法的两种应用：求根和最优化

【数学与算法】牛顿法的两种应用：求根和最优化相关推荐

最新文章

热门文章