3D数学 ---- 矩阵和线性变换

包含平移的线性变换称作仿射变换，3D中的仿射变换不能用 3 x 3 矩阵表达，必须使用4 x 4矩阵。

一般来说，变换物体相当于以相反的量变换描述这个物体的坐标系。当有多个变换时，则需要以相反的顺序变换相反的量。例如，将物体顺时针旋转20度，扩大200%，等价于将坐标系缩小200%，再逆时针旋转20度。

2D中的旋转

在2D环境中，物体只能绕某个点旋转，因为现在暂不考虑平移。这里我们进一步限制物体，使其只绕原点旋转。2D中绕原点的旋转只有一个参数，角度θ，它描述了旋转量。逆时针旋转经常（不是必须）被认为是正方向，顺时针方向是负方向。图8.5展示了基向量p，q绕原点旋转，得到新的基向量p'，q'。

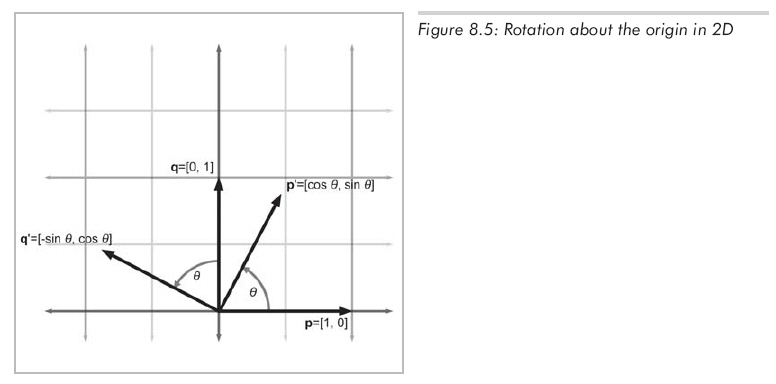
现在我们知道了旋转后基向量的值，就可以以公式8.1的形式构造矩阵如下：

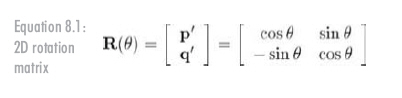
3D中绕坐标轴的旋转

在3D场景中，绕轴旋转而不是点（此时轴指的是旋转所绕的直线，不一定是笛卡尔坐标轴x，y，z）。再次声明，这里暂不考虑平移，所以只讨论旋转轴穿过原点的情况。

绕轴旋转角度θ时，必须知道哪个方向被认为“正”，哪个方向被认为“负”，左手坐标系中定义此方向的规则为左手法则。首先，要明确旋转轴指向哪个方向。当然，旋转轴在理论上是无限延伸的，但我们还是要认为它有正端点和负端点。与笛卡尔坐标轴定义坐标系相同，左手法则是这样的:伸出左手，大拇指向上，其余手指弯曲。大拇指指向旋转轴的正方向，此时，四指弯曲的方向就是旋转的正方向。如图8.6所示。

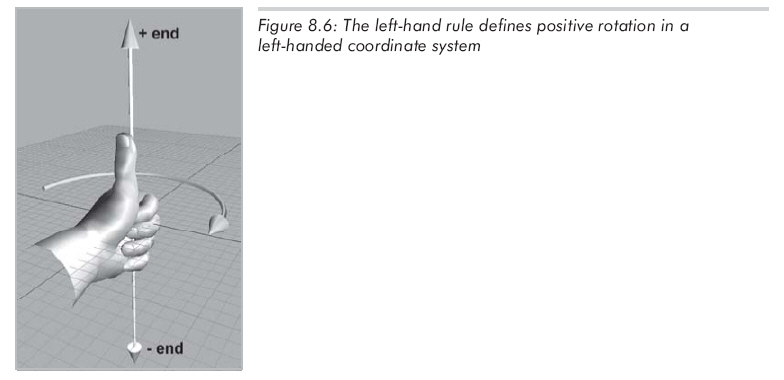
如果用的是右手坐标系，也有类似的法则，不过是用右手代替左手，如图8.7所示：

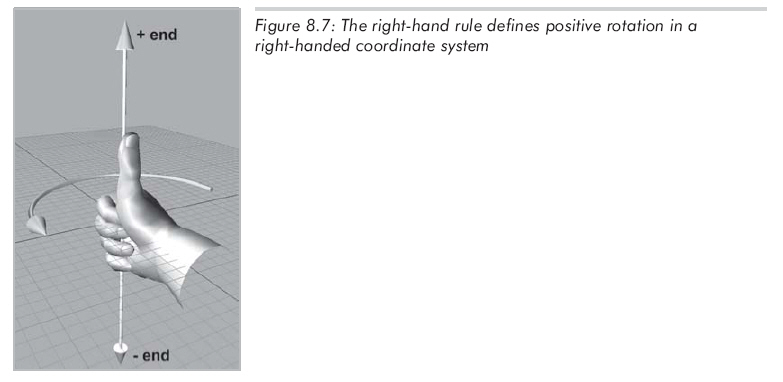
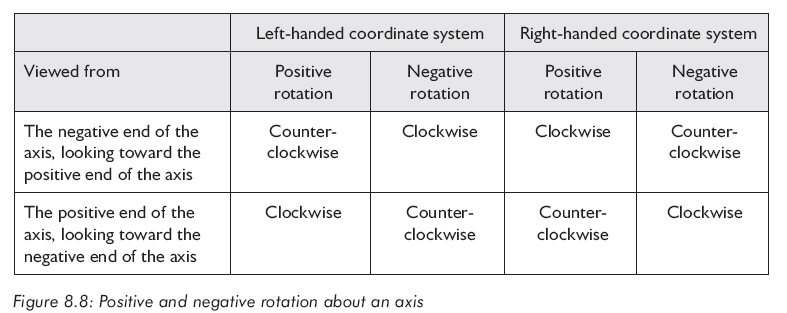
图8.8显示了另一种正方向的定义：

最为常见的旋转是绕某坐标轴的简单旋转，让我们从绕x轴旋转开始，如图8.9所示：

求出旋转后的基向量，可以得到矩阵，见公式8.2。

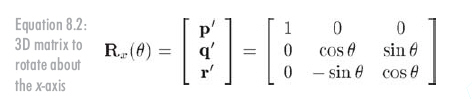
Rotation about the y-axis is similar:

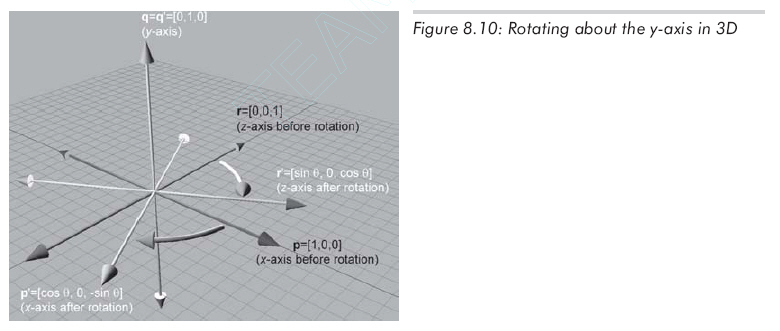
The matrix to rotate about the y-axis:

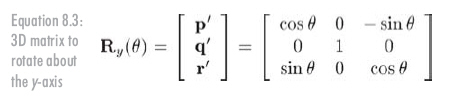
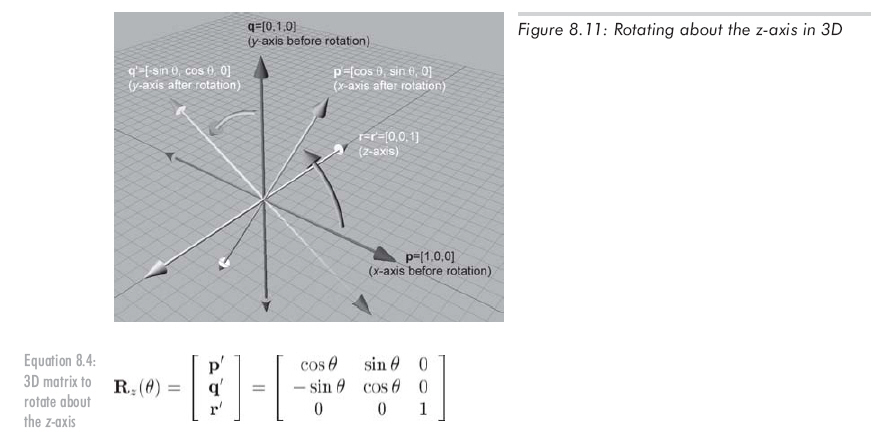
Finally, rotating about the z-axis:

3D中绕任意轴的旋转

当然也能绕3D中的任意轴旋转。因为这里不考虑平移，可以假设旋转轴通过原点，这种旋转比绕坐标轴的旋转更复杂也更少见。用单位向量n描述旋转轴，和前面一样用θ描述旋转量。

让我们导出绕轴n旋转角度θ的矩阵，也就是说，我们想得到满足下面条件的矩阵 R(n, θ)：

vR(n, θ) = v'

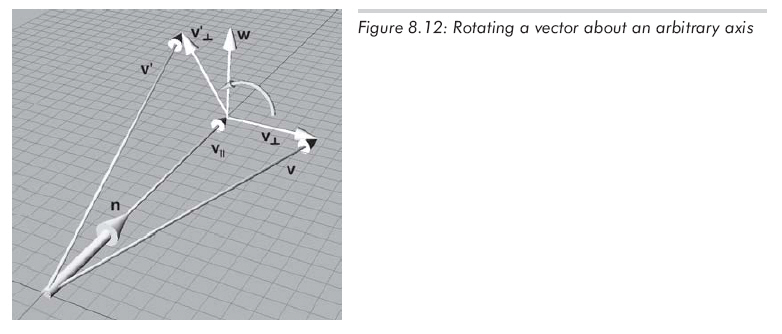
v'是向量v绕轴n旋转后的向量。让我们看看能否用v，n和θ表示v'。我们的想法是在垂直于n的平面中解决这个问题，那么这就转换为了一个简单的2D问题。为了做到这一点，将v分解为两个分量：v||和v⊥，分别平行于n和垂直于n，并有v = v|| + v⊥。因为v||平行于n，所以绕n旋转不会影响它。故只要计算出v⊥绕n旋转后的 v⊥'，就能得到 v' =v|| + v⊥'。为了计算v⊥'，我们构造向量v|| ，v⊥和临时向量w，如图8.12所示：

’

上图展示了以下向量：

（1）v|| 是v平行于n的分量，另一种说法就是v|| 是v在n上的投影，用（v.n）n计算。

（2）v⊥是v垂直于n的分量，因为 v = v|| + v⊥，所以 v⊥ = v - v||。v⊥是v投影到垂直于n的平面上的结果。

（3）w是同时垂直于v||和v⊥的向量，它的长度和v⊥的相同。w和v⊥同在垂直于n的平面中，w是v⊥绕n旋转90度的结果，由n x v⊥可以得到。

现在，v'垂直于n的分量可以表示为：

3D数学 ---- 矩阵和线性变换相关推荐

【3D数学】03 - 线性变换
1. 线性变换线性变换不等同于矩阵,矩阵只是某种线性变换的一种显示的数学表达方式,而且某种确定的线性变换在不同的坐标系中,描述该线性变换的矩阵也不相同. 实际上,如果不在源空间(source) 和 ...
3D图形:矩阵的行列式,矩阵的逆、正交矩阵、齐次矩阵
前言在前面我们说到关于矩阵的一些计算知识,相信大家已经觉得进入了水深火热之中了,那么为了让大家感到更加刺激的视觉体验和感官体验,这一篇博客,我将对矩阵的行列式,矩阵的逆,正交矩阵,齐次矩阵进行探讨研 ...
3D数学读书笔记——矩阵基础番外篇之线性变换
本系列文章由birdlove1987编写.转载请注明出处. 文章链接:http://blog.csdn.net/zhurui_idea/article/details/25102425 前面有一篇文章 ...
Unity中的3D数学—02向量与矩阵
1.向量 1.1 向量的运算运算公式矢量和标量的乘/除法 k v = ( k v x , k v y , k v z ) k\mathbf{v}=(kv_x,kv_y,kv_z) kv=(kvx ...
3D数学-裁剪空间与透视投影矩阵的推导
3D数学-裁剪空间与透视投影矩阵的推导透视投影矩阵的变换本质,是将视锥体变换到裁剪空间中视锥体的具有六个面,近裁剪面,远裁剪面,左裁剪面,右裁剪面,上裁剪面,下裁剪面所有超出视锥体的都会被舍弃, ...
Unity3D for VR 学习(6): 再次温故知新-3D数学
一年前,系统学习过3D数学,并记录了一篇博客<C#程序员整理的Unity 3D笔记(十):Unity3D的位移.旋转的3D数学模型>. 一年后,再次温习之. 坐标系:Unity3D使用左手 ...
线性代数-向量，矩阵，线性变换
一.向量向量要求具有两个条件: 长度(大小) 方向二维: 三维: 计算机中,向量可看做列表: 图中第一个列表有两行我们说它是二维向量,第二个列表有四行,我们说他是四维向量向量的运算向量加法: ...
3D数学系列之——从“蒙的挺准”到“蒙的真准”解密蒙特卡洛积分！
目录 1.前言 2.积分概念简单回顾 3.积分在程序计算上的困难 4.蒙特卡洛积分 5.一些扩展应用 1.前言在学习3D数学的过程中,或者说在学习游戏开发.引擎开发.渲染器开发.Shader开发 ...
matlab 矩阵旋转变换矩阵,matlab 矩阵与线性变换与计算.ppt
matlab 矩阵与线性变换与计算第五章:矩阵与线性变换 1 有限维空间的线性变换是简单而常用的数学变换,其实现可以归结为矩阵运算 y=Ax 刚体的运动,物体的线性变形,光线的反射等,都可以归结为线 ...

3D数学 ---- 矩阵和线性变换

3D数学 ---- 矩阵和线性变换相关推荐

最新文章

热门文章