Dirichlet Tree Distribution(狄利克雷树分布)

标签：#Dirichlet##分布##统计基础#

时间：2017/02/06 21:17:00

作者：小木

这篇博客的主要内容来自于Tom Minka的笔记——[The Dirichlet-tree distribution](https://tminka.github.io/papers/dirichlet/minka-dirtree.pdf "The Dirichlet-tree distribution")

####简介

Dirichlet分布作为多项式分布的先验已经很流行了，但是狄利克雷分布还有两个主要的限制：

1)每一个变量有自己的均值，但是它们却共享一个变量参数

2)除了限制它们的和为1外，变量之间必须相互独立。

这里介绍的Dirichlet-tree分布可以克服上述缺点但保留计算上的简洁。新的分布也可以作为多项式分布的先验。在这里，我们不再把多项式分布的样本看作是一个K面的筛子结果，我们把它看作是一个有限的随机过程的结果。如图1中的(a)所示，一个叶子节点的概率是每个树枝所有的概率乘积。图1中的b图是更一般形式的树。在Dirichlet分布中，参数是叶子节点的概率，即$[p_1 \ldots p_K]$，所以某个样本x的概率为(**注意：这里右上角$\delta(x-k)$是delta函数，又叫Dirac delta function。其值在任意范围内都是0，除了在0位置。因而这里的delta函数就表示当x取k的时候，$\delta(x-k)=1$，否则就是0，那么下式的含义就是某个点的概率就是对应的pk**):

```math

p(x|\textbf{p})=\prod_{k=1}^{K}p_{k}^{\delta(x-k)}

```

在树结构的参数下，这个概率就变成了：

```math

p(x|\textbf{B},T)=\prod_{\text{nodes} \space j}\prod_{\text{branches} \space c}b_{jc}^{\delta_{jc}(x)}

```

```math

\delta_{jc}(x)=

\begin{cases}

1 \space\space \text{if branches jc leads to x} \\

0 \space\space \text{otherwise}

\end{cases}

```

到达内部任意一个节点的概率也可以使用这样的概率表示。这个参数的共轭先验也就不再是一个Dirichlet密度而是一群Dirichlet密度的乘积，每个节点的概率为：

```math

p(\textbf{B}|\alpha) = \prod_{(\text{nodes}\space j)}p(b_j|\alpha)

```

```math

p(b_{j}|\alpha) \sim \mathscr{D}(\alpha_{jc})

```

这里的意思就是每个节点的概率就等于和它直接相连的枝branch c与这个枝上的节点j的概率乘积，如图2中的(b)所示，红色节点的概率就是等于和它直接相连的枝(概率是0.4)和那个蓝色的节点(概率是0.7)的乘积，也就是0.28。而每一个枝都是来自一个Dirichlet先验分布。因此，这里的参数是来自很多歌Dirichlet先验的乘积，而不是原来的一个Dirichlet分布了。这就体现出Dirichlet树分布的优势了，也就是每个子树都可以是用不同的先验控制。



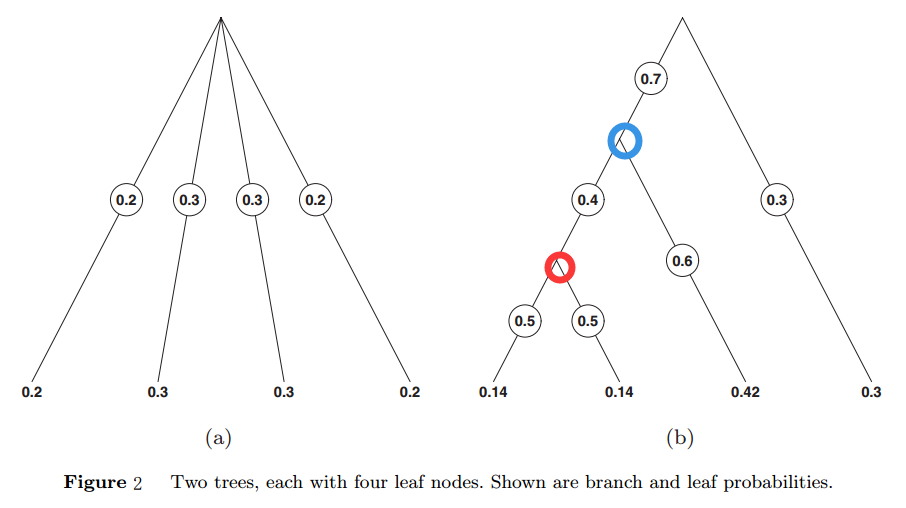
Dirichlet树分布是一个关于叶子概率$[p\_1,...,p\_K]$的分布，这个分布是关于树结构T和$\alpha$的函数。每个节点的概率可以通过如下的公式计算：

```math

b_{jc} = \frac{\sum_{k} \delta_{jc}(k)p_{k}}{\sum_{kc'}\delta_{jc'}(k)p_{k}}

```

也就是说$b\_{jc}$与其子树的概率质量成正比。最终我们可以得到：

```math

p(\textbf{p}|\alpha,T) = \prod_{k} p_{k}^{\alpha_{\text{parent}(k)-1}} \prod_{j} \frac{\Gamma(\sum_{c}\alpha_{jc})}{\prod_{c}\Gamma(\alpha_{jc})} (\sum_{kc}\delta_{jc}(k)p_{k})^{\beta_{j}}

```

```math

\beta_j = \alpha_{\text{parent}(j)}-\sum_{c}\alpha_{jc}

```

当j是根节点时候，$\beta\_{j}$就是0了。每个节点的Dirichlet分布既可以是尖的也可以是宽的，从而使得Dirichlet树分布控制每个$p_k$的形状。