第1章绪论

1.1 计算机与算法

算法需要具备的要素

输入、输出
正确性
确定性
可行性
有穷性

有穷性反例：Hailstone Sequence

Hailstone(n)={{1},if n equal 1{n}∪Hailstone (n/2),if nis even {n}∪Hailstone (3n+1),if is odd Hailstone (n)=\left\{\begin{array}{ll}\{1\}, & \text { if n equal } 1 \\ \{n\} \cup \text { Hailstone }(n / 2), & \text { if } \mathrm{n} \text { is even } \\ \{n\} \cup \text { Hailstone }(3 n+1), & \text { if is odd }\end{array}\right. Hailstone(n)=⎩⎨⎧{1},{n}∪ Hailstone (n/2),{n}∪ Hailstone (3n+1), if n equal 1 if n is even if is odd

因为至今尚不确定该序列是否具有有穷性，所以下面计算该序列长度的程序还不能被称之为算法。

int hailstone(int n)
{int length = 1;while(n > 1){n % 2 ? n = 3 * n + 1 : n /= 2;length++;}return length;
}

符合有穷性的算法示例：Bubble Sort

将n个整数按照通常的大小次序排成一个非降序列，以下是一种排列算法Bubble Sort

void bubbleSort(int A[], int n)
{bool sorted = false; //整体排序标志，初始化为未排序while (!sorted)      // 无法确定完成排序，则逐趟扫描{sorted = true;for (int i = 1; i < n; i++){if (A[i - 1] > A[i]) // 如果有两个相邻的数构成逆序{swap(A[i - 1], A[i]); //交换sorted = false;       // 无法确定完成排序}}n--; // 每扫描一趟必有扫描范围内的最大值来到序列尾，扫描范围减1}
}

我们发现，每次扫描必然会将扫描范围内最大的数放置到扫描范围的尾部，所以排序的过程一定是有穷的。

排序过程中，所有元素朝各自最终位置亦步亦趋的移动过程如同气泡在水中浮动，这个算法也因此得名。

1.2 复杂度度量

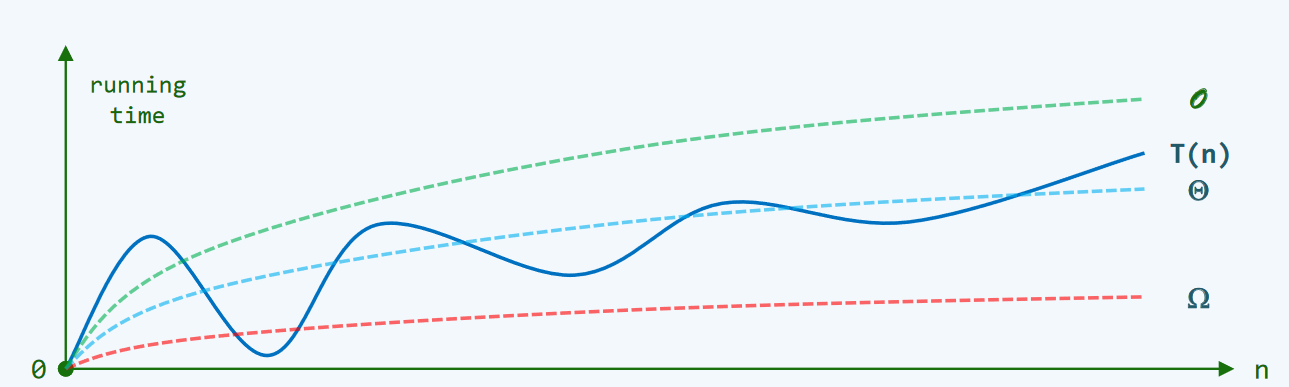
三条虚线由上到下分别表示：最坏情况下的复杂度（最基本最常用）、较为准确的复杂度（始终与程序运行时间同阶）、最好情况下的复杂度

1.3 复杂度分析

1.3.1 常数O(1)

运算时间可表示为T(n) = O(1)的算法，统称作常数时间复杂度算法，是最为理想的算法，一般仅含一次或常数次基本操作，通常不含循环、分支、子程序调用等，但是不能根据形式一概而论。

1.3.2 对数O(logn)

示例算法：统计某非负整数二进制展开后数位1的总数

int countOnes(unsigned int n)
{int ones = 0; // 负责计数while (n > 0){ones += (1 & n); //最低位若为1则计数n >>= 1;         //右移一位}
}

复杂度分析

n的二进制展开总位数是(log₂n) +1, 那么循环次数自然也是((log₂n) +1，而无论在循环体之内还是之外，均只有常数次操作，因此该算法的执行时间主要由循环次数决定，又
∀a,b>1,log⁡an=log⁡ab⋅log⁡bn=Θ(log⁡bn)\forall a, b>1, \log _{a} n=\log _{a} b \cdot \log _{b} n=\Theta\left(\log _{b} n\right) ∀a,b>1,logan=logab⋅logbn=Θ(logbn)
可知，常底数的具体取值无所谓，故不再标出而记作logn，此类算法称作具有对数复杂度
∀c>0,log⁡nc=c⋅log⁡n=Θ(log⁡n)\forall c>0, \log n^{c}=c \cdot \log n=\Theta(\log n) ∀c>0,lognc=c⋅logn=Θ(logn)
可知，常数次幂的具体取值也无所谓
123⋅log⁡321n+log⁡205(7⋅n2−15⋅n+31)=Θ(log⁡321n)123 \cdot \log ^{321} n+\log ^{205}\left(7 \cdot n^{2}-15 \cdot n+31\right)=\Theta\left(\log ^{321} n\right) 123⋅log321n+log205(7⋅n2−15⋅n+31)=Θ(log321n)

O(log⁡cn)O\left(\log ^{c} n\right) O(logcn)

更一般地，复杂度如上式的算法，均可称作对数多项式复杂度（O(logn)是c=1的特殊情况），这种算法的效率不如常数O(1)但无限接近与它。

1.3.3 线性O(n)

示例算法：计算n个整数的和

int sumI(int A[], int n)
{int sum = 0;  //O(1)for (int i = 0; i < n; i++) //O(n)sum += A[i];    //O(1)return sum;   //O(1)
}

复杂度分析

O(1) + O(n) * O(1) + O(1) = O(n + 2) = O(n)

运算时间可表示为T(n) = O(n)的算法，统称作线性时间复杂度算法

1.3.4 多项式O( polynomial ( n ) )

示例算法：Bubble Sort

void bubbleSort(int A[], int n)
{bool sorted = false; //整体排序标志，初始化为未排序while (!sorted)      // 无法确定完成排序，则逐趟扫描 O(n-1){sorted = true;for (int i = 1; i < n; i++) // O(n-1){if (A[i - 1] > A[i]) // 如果有两个相邻的数构成逆序  {swap(A[i - 1], A[i]); //交换 O(1)sorted = false;       // 无法确定完成排序}}n--; // 每扫描一趟必有扫描范围内的最大值来到序列尾，扫描范围减1}
}

复杂度分析

该算法由内外两层循环构成

内循环依次比较个相邻元素（n - 1次），如有必要则进行交换（至多n - 1 次），一轮内循环至多需要执行2 * (n - 1)次基本操作
前面分析过，外循环至多执行(n - 1)轮，则总共执行的基本操作至多 2 * (n - 1)²次
进一步简化整理可得：T(n) = O(n²)

若运行时间可以表示和度量为T(n) = O( f(n) )的形式，而且f(x)为多项式，则对应算法的称为多项式时间复杂度算法，理论上，复杂度为O(n²⁰²⁰)和O(n¹)均属于该类（线性时间复杂度是多项式时间复杂度的特例）

1.3.5 指数O(2ⁿ)

从O(n^c)到O(2ⁿ)往往被视为有效算法到无效算法的分水岭

示例算法：对任意非负数n，计算幂2ⁿ（蛮力迭代版）

_int64 power2BF(int n)
{_int64 pow = 1; //初始化累积器O(1)while (n--)     // 循环 O(n) 递减 O(1)pow <<= 1;  // ×2 O(1)return pow;     // O(1)
}

复杂度分析

O(1) + O(n) * 2O(1) + O(1) = O(n)，以n本身作为输入规模，运行时间为O(n)

如果按照输入指数n的二进制位数r = 1 + log₂n作为输入规模，则运行时间为O(2^r)

对算法复杂度的界定，都是相对于问题输入规模而言的，输入规模可定义为用以描述输入所需的空间规模，因此，对于该算法，n的二进制展开的宽度r作为输入规模更加合理，countOnes算法也是如此，以输入参数本身的数值作为基准得到的复杂度称作伪××复杂度

一般地，凡运行时间可以表示和度量为T(n) = O(aⁿ) 形式的算法(a>1)，均属于指数时间复杂度算法。

1.3.6 复杂度层次

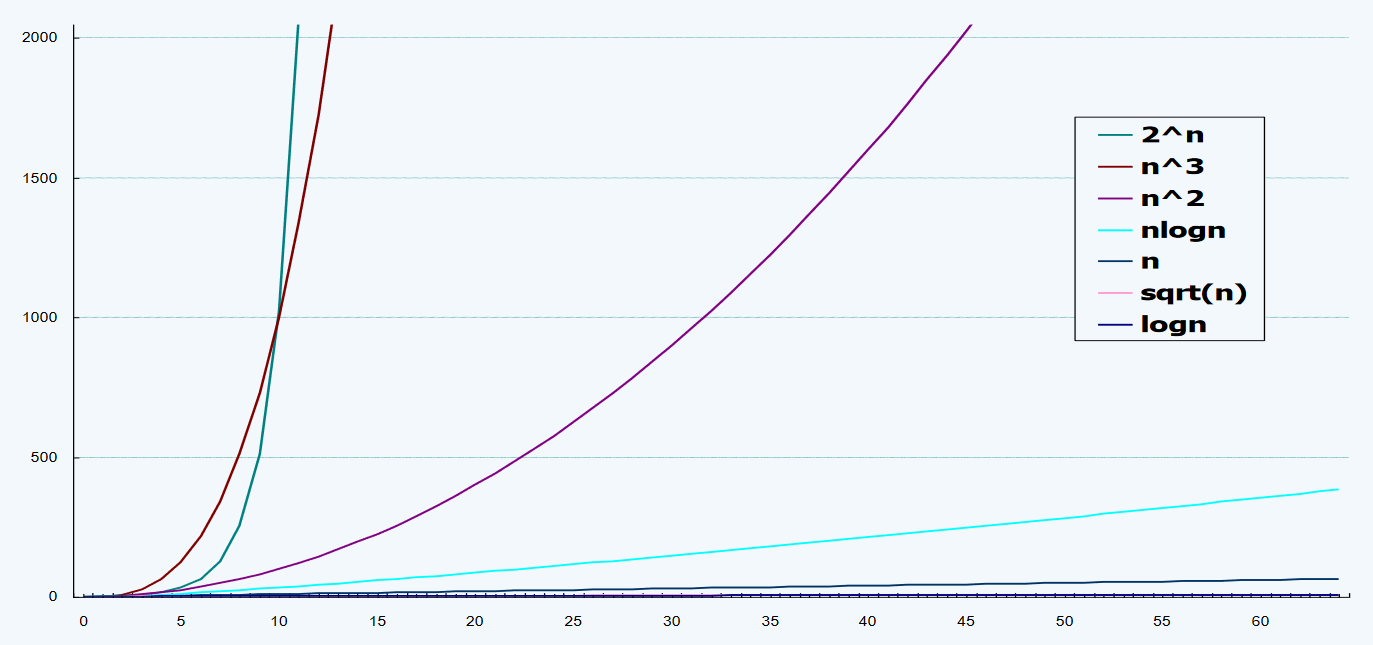
补充：级数

算术级数：与末项平方同阶

T(n)=1+2+…+n=(n+12)=n(n+1)2=O(n2)T(n)=1+2+\ldots+n=\left(\begin{array}{c} n+1 \\ 2 \end{array}\right)=\frac{n(n+1)}{2}=\mathcal{O}\left(n^{2}\right) T(n)=1+2+…+n=(n+12)=2n(n+1)=O(n2)

幂方级数：比幂次高出一阶

∑k=0nkd≈∫0nxddx=xd+1d+1∣0n=nd+1d+1=O(nd+1)\sum_{k=0}^{n} k^{d} \approx \int_{0}^{n} x^{d} d x=\left.\frac{x^{d+1}}{d+1}\right|_{0} ^{n}=\frac{n^{d+1}}{d+1}=\mathcal{O}\left(n^{d+1}\right) k=0∑nkd≈∫0nxddx=d+1xd+1∣∣∣∣0n=d+1nd+1=O(nd+1)

例如：
T3(n)=∑k=1nk3=13+23+33+…+n3=n2(n+1)2/4=O(n4)T_{3}(n)=\sum_{k=1}^{n} k^{3}=1^{3}+2^{3}+3^{3}+\ldots+n^{3}=n^{2}(n+1)^{2} / 4=\mathcal{O}\left(n^{4}\right) T3(n)=k=1∑nk3=13+23+33+…+n3=n2(n+1)2/4=O(n4)

几何级数：与末项同阶

Ta(n)=∑k=0nak=a0+a1+a2+a3+…+an=an+1−1a−1=O(an),1<aT_{a}(n)=\sum_{k=0}^{n} a^{k}=a^{0}+a^{1}+a^{2}+a^{3}+\ldots+a^{n}=\frac{a^{n+1}-1}{a-1}=\mathcal{O}\left(a^{n}\right), \quad 1<a Ta(n)=k=0∑nak=a0+a1+a2+a3+…+an=a−1an+1−1=O(an),1<a

收敛级数：全部为O(1)

不收敛但有限:

调和级数：
h(n)=∑k=1n1k=1+12+13+14+…+1n=ln⁡n+γ+O(12n)=Θ(log⁡n)h(n)=\sum_{k=1}^{n} \frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\ldots+\frac{1}{n}=\ln n+\gamma+\mathcal{O}\left(\frac{1}{2 n}\right)=\Theta(\log n) h(n)=k=1∑nk1=1+21+31+41+…+n1=lnn+γ+O(2n1)=Θ(logn)
对数级数：
∑k=1nln⁡k=ln⁡∏k=1nk=ln⁡n!≈(n+0.5)⋅ln⁡n−n=Θ(n⋅log⁡n)\sum_{k=1}^{n} \ln k=\ln \prod_{k=1}^{n} k=\ln n ! \approx(n+0.5) \cdot \ln n-n=\Theta(n \cdot \log n) k=1∑nlnk=lnk=1∏nk=lnn!≈(n+0.5)⋅lnn−n=Θ(n⋅logn)

1.4 递归

1.4.2 两种递归分析方法

递归跟踪(recursion trace)

一种直观且可视的方法，按照下面的规则将递归算法的执行过程整理为图的形式：

算法的每一递归实例都表示为一个方框，其中注明了该实例调用的参数
若实例M调用实例N，则在M与N对应的方框之间添加一条有向联线

递推方程(recursion equation)

通过对递归模式的数学归纳，导出复杂度定界函数的递推方程（组）及其边界条件（分析递归基），从而将复杂度的分析，转化为递归方程（组）的求解。

算法分析1：数组求和

1. Decrease-and-conquer

线性递归的模式往往对于减而治之的算法策略，递归每深入一层，待求解问题的规模都缩减一个常数，直至最终蜕化为平凡的小（简单）问题。

int sum(int A[], int n)
{if (n < 1) // 平凡情况，递归基   判断O(1)return 0;else // 一般情况return sum(A, n - 1) + A[n - 1];    // 相加O(1),返回O(1)
}

递归跟踪：

由此可见，递归深度（即任一时刻的活跃递归实例的总数）最大为n+1，T(n) = (n+1)*O(n) = O(n)，而且空间复杂度线性正比于递归深度，亦为O(n)

递推方程：

解决问题sum(A, n) = 解决问题sum(A, n - 1) + A[n - 1] = …

可以得到一般性递推关系：T(n) =T(n - 1) + O(1) =T(n - 1) + c₁ = … = T(0) + nO(1)，其中c₁为常数

另一方面，当递归过程抵达递归基时，求解平凡问题sum(A, 0)只需（用于直接返回0的）常数时间。如此，即可获得如下边界条件：

T(0) = O(1) = c₂，其中c₂为常数

由上述两个方程可以得到T(n) = c₁n + c₂ = O(n)

2. Divide-and-conquer

为了求解大规模问题，可以将其划分为若干个子问题（通常为大小相同的两个）分别求解子问题，然后合并子问题的解得到原问题的解，这就是分而治之的策略。

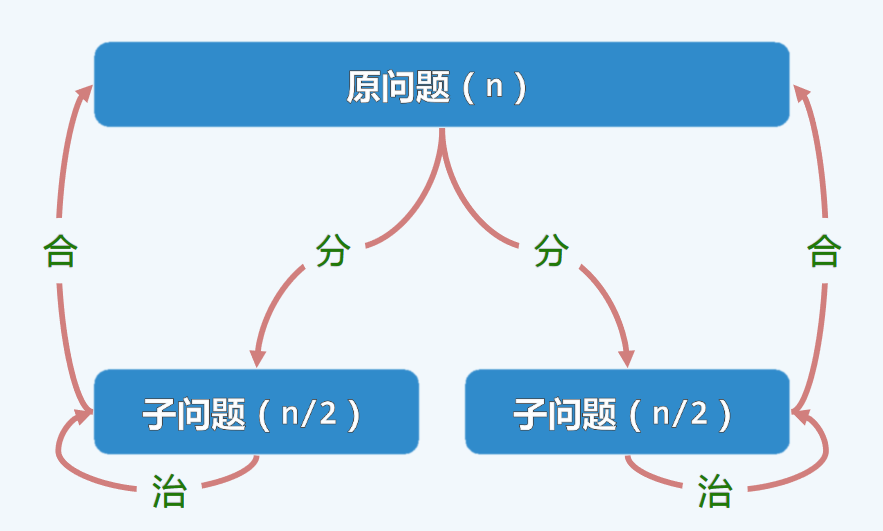
int sum(int A[], int lo, int hi) //区间范围是[lo,hi)
{if (hi - lo < 2)    //O(1)return A[lo];int mi = (lo + hi) >> 1;                //以屁中单元为界，将原匙间一分为二    O(1)return sum(A, lo, mi) + sum(A, mi, hi); //递归对各子数组求和，然后合计 2*O(n/2)
}

递归跟踪：

T(n) = 各层递归实例所需时间之和 = O(1) * (2⁰ + 2¹ + 2² + … + 2^log₂n)

这符合我们前面所说的几何级数，故T(n) = O(n)

相对于前面线性递归算法，二分递归算法的递归深度不会超过log₂n+1，即空间复杂度为O(logn)，小于线性递归的O(n).

递推公式：

T(1) = O(1)

T(n) = 2 * T(n/2) + O(1) = 4 * T(n/4) + O(3) = … = n * T(1) + O(n - 1) = O(2n - 1) = O(n)

算法分析2：Fibonacci Sequence

fib(n)={n(n≤1)fib(n−1)+fib(n−2)(n≥2)f i b(n)=\left\{\begin{array}{ll} n & \left( n \leq 1\right) \\ f i b(n-1)+f i b(n-2) & \left( n \geq 2\right) \end{array}\right. fib(n)={nfib(n−1)+fib(n−2)(n≤1)(n≥2)

1. Divide-and-conquer

_int64 fib1(int n)
{return (n < 2) ? n : fib1(n - 1) + fib1(n - 2);    //O(n-1)+O(n-2)+O(1)
}

递归跟踪：

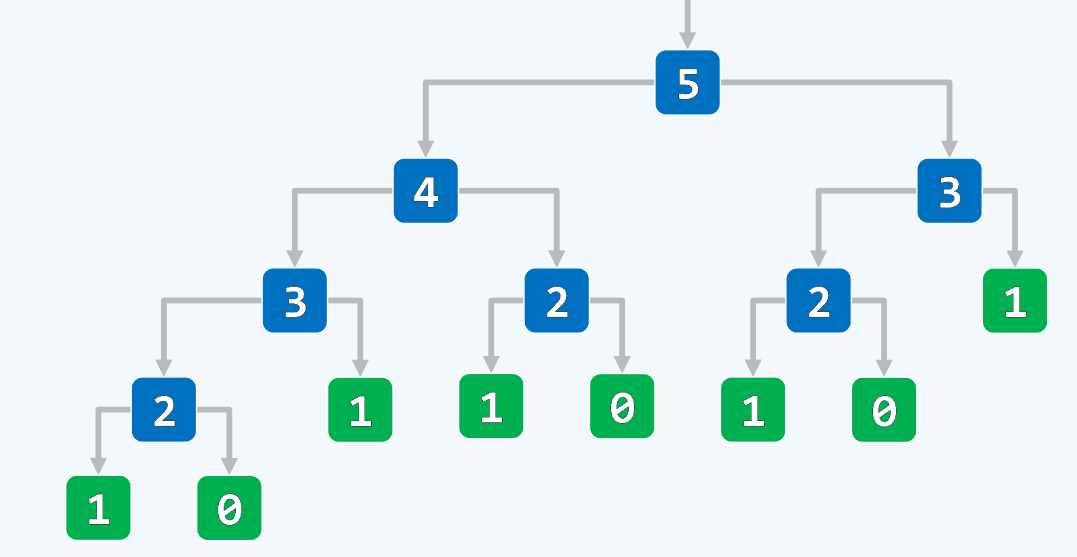
T(n) = 各层递归实例所需时间之和 = O(1) * (2⁰ + 2¹ + 2² + … + 2ⁿ)

故，T(n) = 2ⁿ，这个时间复杂度让人无法接受，原因在于：计算过程中所出现的递归实例重复度极高，同一个Fibonacci数计算了多次，使得效率很低

递推公式：

见习题解析P13，教材P24

2. 优化策略之记忆：Decrease-and-conquer

为了消除递归算法中重复的递归实例，一种自然而然的思路可以概括为：

借助一定量的辅助空间，在各子问题求解之后，及时记录下其对应的解答

其中，和分而治之一样自顶向下，但每次遇到一个子问题都先查验它是否已经计算过，以期通过直接调阅记录获得解答，从而避免重新计算，称之为制表或记忆策略

//prev = fib(n-1)   prevPrev = fib(n-2)
//令fib(-1) = 1,有fib(1) = fib(-1) + fib(0) = 1之意
_int64 fib2(int n, _int64 &prev)
{if (n == 0) //若到达了递归基即fib(0){prev = 1;  //fib(-1) = 1return 0; //fib(0) = 0}else{_int64 prevPrev;prev = fib2(n - 1, prevPrev); //递归计算前两项return prev + prevPrev;       //其和即位正解}
}

这里将二分递归中的fib(n-2)省略，而是通过变量prevPrev（被记忆）调阅此前记录来直接获得（个人想法：递归由下至上返回时，下一层的prev传递到上一层作为prevPrev，下一层的返回值在上一层中赋给prev，这里所说的上一层的返回值就是prev + prevPrev。每返回至一个上层递归，都用下层的prev更新上层的prevPrev，用下层的返回值更新上层的prev）

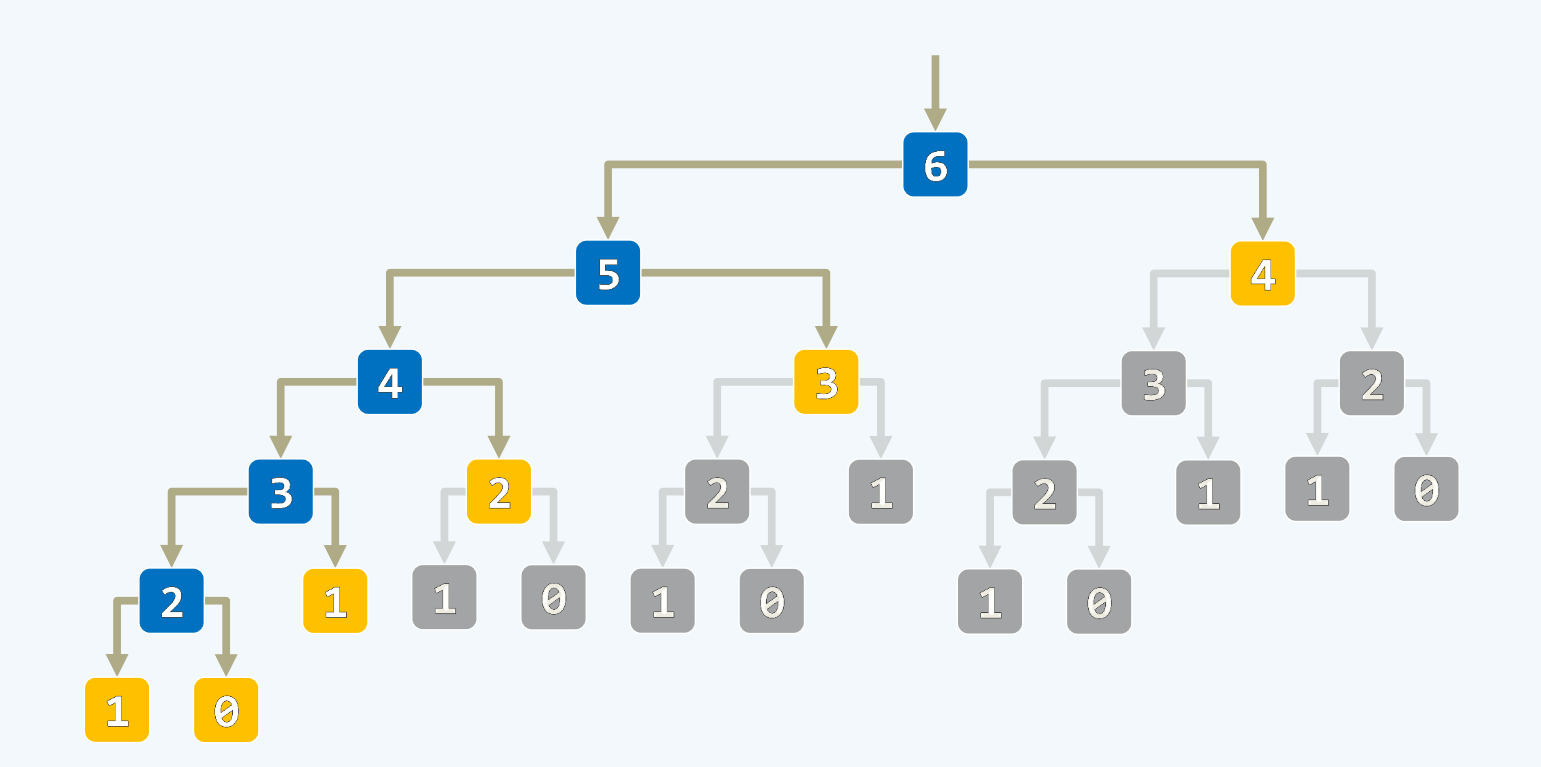
**该算法呈线性递归模式，递归的深度线性正比于输入n，前后共计仅出现O(n)个递归实例，累计耗时不超过O(n)。**遗憾的是，该算法共需使用O(n)规模的附加空间，下面的动态规划策略可以更好解决这个问题。

3. 优化策略之动态规划：迭代

从递归基出发，自底而上递推地得出各子问题的解，直至最终原问题的解，为动态规划策略。

_int64 fib3(int n)
{_int64 f = 0, g = 1; //fib(0) = 0   fib(1) = 1if (n == 0)return 0;while (n-- > 0) //O(n){g = g + f;f = g - f;}return g;
}

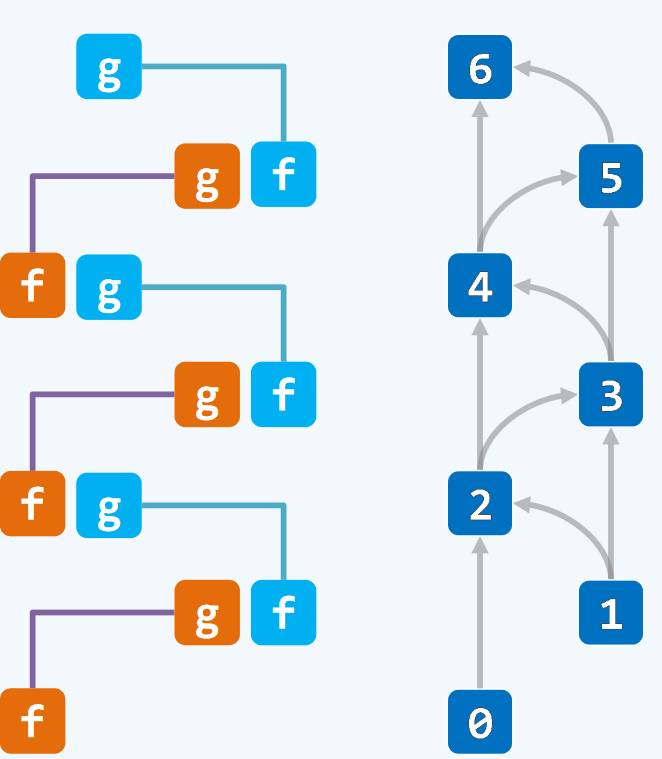
T(n) = O(n) 且仅需O(1)的空间

算法分析3：最长公共子序列(LCS)

怎样解决问题：递归

对于序列A[0, n)和B[0, m)，LCS(n , m)有以下三种情况：

若n =-1或m = -1，则取空序列("") 递归基
若A[n] = ‘X’ = B[m]，则取作：LCS(n - 1 , m -1) + ‘X’ Decrease-and-conquer
若A[n] != B[m], 则考虑两种情况，LCS(n, m - 1)与LCS(n - 1, m)，然后在这两者中取更长者 Divide-and-conquer

**个人对上图的理解：**从右下角开始，遇到分而治之的情况（即比较的两个字符不相等），就向←和↑衍生出两个新的递归实例；遇到减而治之的情况（两个字符相等），就沿左上方对角线，衍生出一个递归实例，直到递归到左上角的递归基。

到达递归基后开始返回调用，具有返回调用关系的递归实例之间相连，遇到一个对角线（即两字符相等）则LCS长度加一（对角线左上方数字加一得到右下方），对于分治情况，需要从该递归实例的上方和左边选择长度更大（即数字更大）的返回。按上述规则对各递归实例进行连接后得到上图，而这些连线形成的每个单调通路就对应该问题的一个解。

分析复杂度：

选取一个局部递归过程观察，图中大量递归实例发生雷同（同时被两个箭头所指）

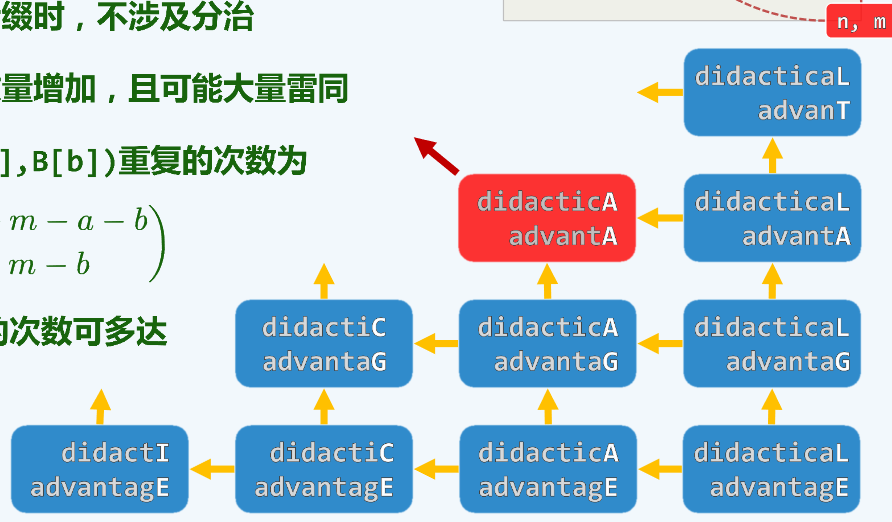
由(n,m)唤醒(a,b)的数量等于(n,m)到(a,b)通路的数量，特别地，当(a,b)取(0,0)，n=m时，LCS(0,0)的次数可达O(2ⁿ)

怎样提高效率：动态规划

去除重复的大量递归实例后，我们发现，所有子问题不过O(n * m)个，我们可以采用动态规划，颠倒顺序，从左上角开始，花费O(n * m)时间，计算出所有子问题。计算的规则是：碰到两个字母相同的情况（减而治之），则对应位置的数字为它的左上角数字加1；碰到两个字母不相同的情况（分而治之），则对应位置的数字为它的上方和左边的数字的最大者。得到下图：

其中通过加1得到的1，2，3，4任意一种组合即为LCS的一个解。

1.5 ADT

在数据结构的具体实现与实际应用之间，ADT就分工和接口制定了统一标准。

其中的

实现：高效兑现数据结构的ADT接口操作
应用：便捷地通过操作接口使用数据结构

Chapter 1 复杂度分析和递归分析相关推荐

【每日一学】复杂度分析
文章目录目标什么是数据结构复杂度分析目标建立时间复杂度.空间复杂度意识,写出高质量的代码能够设计基础架构提高编程技能训练逻辑思维什么是数据结构广义:一组数据的存储结构 | 操作数据 ...
卷积神经网络的复杂度分析
点击上方"视学算法",选择加"星标"或"置顶" 重磅干货,第一时间送达作者 | Michael Yuan@知乎(已授权) 来源 | htt ...
QIIME 2教程. 08差异丰度分析gneiss(2021.2)
QIIME 2用户文档. 8差异丰度分析gneiss Differential abundance analysis with gneiss 原文地址:https://docs.qiime2.org/ ...
QIIME 2用户文档. 7差异丰度分析gneiss(2018.11)
文章目录前情提要 QIIME 2用户文档. 7差异丰度分析gneiss 创建`balances` 选项1:相关性聚类选项2:梯度聚类用平衡建立线性模型 Reference 译者简介猜你喜欢写 ...
QIIME 2教程. 08差异丰度分析gneiss(2020.11)
文章目录 QIIME 2用户文档. 8差异丰度分析gneiss 创建`balances` 方法1:相关性聚类选项2:梯度聚类 Reference 译者简介猜你喜欢写在后面 QIIME 2用户文档 ...
快速谱峭度matlab,一种基于快速谱峭度分析的泵潜在空化故障检测方法与流程
本发明属于信号处理领域,尤其涉及一种基于快速谱峭度分析泵的实时状态并且检测其潜在空化故障的方法. 背景技术: 高性能离心泵在当今社会上广泛应用和需求巨大.由于工作在高压高速等复杂条件下,离心泵的空化故 ...
python jieba 文本相似度_文本相似度分析（基于jieba和gensim）
##基础概念本文在进行文本相似度分析过程分为以下几个部分进行, 文本分词语料库制作算法训练结果预测分析过程主要用两个包来实现jieba,gensim jieba:主要实现分词过程 gensi ...
算法录之复杂度分析。
一个算法的复杂度可以说也就是一个算法的效率,一般来说分为时间复杂度和空间复杂度... 注意接下来说的均是比较YY的,适用与ACM等不需严格分析只需要大致范围的地方,至于严格的算法复杂度分析的那些数学证 ...
算法之如何进行算法复杂度分析
一.什么是复杂度分析? 1.数据结构和算法解决是"如何让计算机更快时间.更省空间的解决问题". 2.因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能. 3.分别用时间复 ...

Chapter 1 复杂度分析和递归分析

第1章 绪论

1.1 计算机与算法

算法需要具备的要素

有穷性反例：Hailstone Sequence

符合有穷性的算法示例：Bubble Sort

1.2 复杂度度量

1.3 复杂度分析

1.3.1 常数O(1)

1.3.2 对数O(logn)

示例算法：统计某非负整数二进制展开后数位1的总数

复杂度分析

1.3.3 线性O(n)

示例算法：计算n个整数的和

复杂度分析

1.3.4 多项式O( polynomial ( n ) )

示例算法：Bubble Sort

复杂度分析

1.3.5 指数O(2n)

示例算法：对任意非负数n，计算幂2n（蛮力迭代版）

复杂度分析

1.3.6 复杂度层次

补充：级数

算术级数：与末项平方同阶

幂方级数：比幂次高出一阶

几何级数：与末项同阶

收敛级数：全部为O(1)

不收敛但有限:

1.4 递归

1.4.2 两种递归分析方法

递归跟踪(recursion trace)

递推方程(recursion equation)

算法分析1： 数组求和

1. Decrease-and-conquer

2. Divide-and-conquer

算法分析2：Fibonacci Sequence

1. Divide-and-conquer

2. 优化策略之记忆：Decrease-and-conquer

3. 优化策略之动态规划：迭代

算法分析3：最长公共子序列(LCS)

怎样解决问题：递归

怎样提高效率：动态规划

1.5 ADT

Chapter 1 复杂度分析和递归分析相关推荐

最新文章

热门文章

第1章绪论

1.3.5 指数O(2ⁿ)

示例算法：对任意非负数n，计算幂2ⁿ（蛮力迭代版）

算法分析1：数组求和