支持向量机专题——线性可分支持向量机

原文

支持向量机(support vector machine, SVM)是一种经典的分类器，其主要思想是学习一个在特征空间上使间隔最大的分类器。支持向量机的学习可以看成是一个求解凸二次规划问题的过程，同时也等价于正则化的合页损失函数的最小化问题。

支持向量机可以分为：线性可分支持向量机、线性支持向量机、非线性支持向量机三种。当训练数据线性可分时，可通过硬间隔最大化，学习一个线性可分支持向量机（也称为硬间隔支持向量机）；当训练数据近似线性可分时，可以通过软间隔最大化，学习一个线性支持向量机（也称为软间隔支持向量机）；当训练数据线性不可分时，需要使用核技巧，学习非线性支持向量机。

线性可分支持向量机

问题抽象

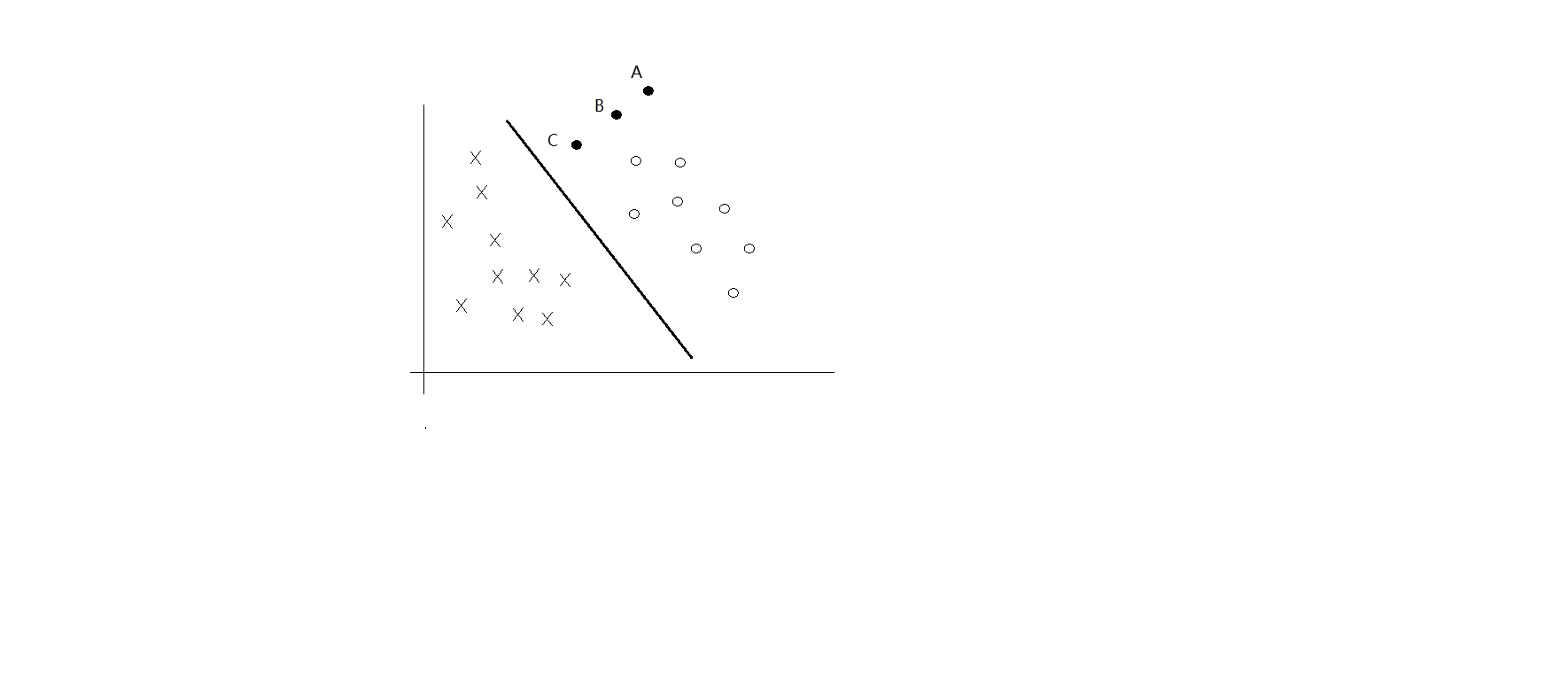
一般来说，一个点距离超平面的距离可以表示分类预测的确信程度，如图所示，点C、B、A分类的确信程度依次递增。 |ω⋅x+b| |\omega\cdot x+b| 可以表示点 x x距离超平面的远近。这个“远近”有个名字叫函数间隔。

γ^i=yi(ω⋅xi+b)

\hat \gamma_i=y_i(\omega\cdot x_i+b)

令

γ^=mini=1...Ny^i

\hat \gamma = \min_{i=1...N}\hat y_i

线性可分支持向量机的目的就是找到使 γ^ \hat \gamma最小的超平面。

函数间隔不足以表示分类预测的确信度，因为如果成倍的增加 ω \omega和 b b的值，超平面并没有改变，但是函数间隔却也同样成倍增加，这显然是不合理的。因此不妨引入几何间隔 ，使间隔是确定的

γi=ω||ω||⋅xi+b||ω||

\gamma_i = \frac{\omega}{||\omega||}\cdot x_i + \frac{b}{||\omega||}
显然，函数间隔和几何间隔存在以下关系

γi=γ^i||ω||

\gamma_i=\frac{\hat \gamma_i}{||\omega||}
支持向量机学习的基本想法是求解能正确划分训练数据集并且几何间隔最大的分离超平面，对线性可分的数据集而言，这个超平面是唯一的。

求解最大间隔分离超平面的问题可以表示为下面的约束最优化问题：

maxω,bγ

\max_{\omega,b}\qquad\gamma

s.t.yi(ω||ω||⋅xi+b||ω||)≥γ

s.t.\qquad y_i(\frac{\omega}{||\omega||}\cdot x_i+\frac{b}{||\omega||})\ge\gamma

意思就是要让最小间隔最大化

根据几何间隔和函数间隔的关系，该问题可以改写为

maxω,bγ^||ω||

\max_{\omega,b}\qquad\frac{{\hat \gamma}}{||\omega||}

s.t.yi(ω⋅xi+b)≥γ^

s.t. \qquad y_i(\omega\cdot x_i+b)\ge\hat\gamma

由于将 ω \omega和 b b等比例缩放λ\lambda倍，函数间隔变成 λγ^ \lambda \hat \gamma ，因此， γ^ \hat\gamma的取值对最优化问题的解无影响，因此不妨设 γ^ \hat\gamma的值为,于是等价于以下最优化问题的解

maxω,b1||ω||

\max_{\omega,b}\qquad\frac{1}{||\omega||}

s.t.yi(ω⋅xi+b)≥1

s.t.\qquad y_i(\omega\cdot x_i+b)\ge1

等价于

minω,b12||ω||2

\min_{\omega,b}\qquad\frac{1}{2}||\omega||^2

s.t.yi(ω⋅xi+b)−1≥0

s.t.\qquad y_i(\omega\cdot x_i+b)-1\ge0

这是一个凸二次规划问题,要求 ω∗ \omega^*和 b∗ b^* ，使其满足上式，从而得出最大间隔分离超平面。

最优化问题求解

对于上述抽象问题，可以通过求解原始问题的对偶问题得到最优解，使用这种方式的原因是对偶问题更加容易求解,并且可以自然地引入核函数，从而推广到非线性分类问题

首先构建拉格朗日函数:

L(ω,b,α)=12||ω||2−∑i=1Nαiyi(ω⋅xi+b)+∑i=1Nαi

L(\omega,b,\alpha)=\frac{1}{2}{||\omega||}^2-\sum_{i=1}^N\alpha_iy_i(\omega\cdot x_i+b)+\sum_{i=1}^N \alpha_i

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题

maxαminω,bL(ω,b,α)

\max_{\alpha}\min_{\omega,b}L(\omega,b,\alpha)

因此，需要先求 L(ω,b,α) L(\omega,b,\alpha)对 ω,b \omega,b的极小，再对 α \alpha求极大

求 minω,bL(ω,b,α) \min_{\omega,b}L(\omega,b,\alpha)

将拉格朗日函数对 ω,b \omega,b偏导并令其等于0

ΔωL(ω,b,α)=ω−∑i=1Nαiyixi=0

\Delta_{\omega}L(\omega,b,\alpha) = \omega-\sum_{i=1}^{N}\alpha_iy_ix_i=0

ΔbL(ω,b,α)=∑i=1Nαiyi=0

\Delta_bL(\omega,b,\alpha)=\sum_{i=1}^{N}\alpha_iy_i = 0

得

ω=∑i=1Nαiyixi

\omega = \sum_{i=1}^{N}\alpha_iy_ix_i

∑i=1Nαiyi=0

\sum_{i=1}^{N}\alpha_iy_i=0

将上式代入拉格朗日函数，即得

L(ω,b,α)==12∑i=1N∑j=1Nαiαjyiyj−∑i=1Nαiyi((∑j=1Nαjyjxj)⋅xi+b)+∑i=1Nαi−12∑i=1N∑j=1Nαiαjyiyj∗(xi⋅xj)+∑i=1Nαi

\begin{eqnarray*} L(\omega,b,\alpha) &=& \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j-\sum_{i=1}^{N}\alpha_iy_i((\sum_{j=1}^{N}\alpha_jy_jx_j)\cdot x_i+b)+\sum_{i=1}^{N}\alpha_i \\ &=&-\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j*(x_i\cdot x_j)+\sum_{i=1}^{N}\alpha_i\end{eqnarray*}

接下来要求 L(ω,b,α) L(\omega,b,\alpha)对 α \alpha的极大，即

maxα−12∑i=1N∑j=1Nαiαjyiyj∗(xi⋅xj)+∑i=1Nαi

\max_{\alpha}\, -\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j*(x_i\cdot x_j)+\sum_{i=1}^{N}{\alpha_i}

s.t.∑i=1Nαiαiyi=0≥0,i=1,2,...,N

\begin{eqnarray*}s.t.\quad &\sum_{i=1}^{N}&\alpha_iy_i=0\\&\alpha_i&\ge0\,,\qquad i=1,2,...,N\end{eqnarray*}

该问题可以转化为以下求极小问题

minα12∑i=1N∑j=1Nαiαjyiyj∗(xi⋅xj)+∑i=1Nαi

\min_{\alpha}\, \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j*(x_i\cdot x_j)+\sum_{i=1}^{N}{\alpha_i}

s.t.∑i=1Nαiαiyi=0≥0,i=1,2,...,N

\begin{eqnarray*}s.t.\quad &\sum_{i=1}^{N}&\alpha_iy_i=0\\&\alpha_i&\ge0\,,\qquad i=1,2,...,N\end{eqnarray*}

因此，只需找出满足条件的 α \alpha便能得到该问题最优解

ω∗=∑i=1mα∗iyixib∗=yj−∑i=1Nα∗iyi(xi⋅xj)

\begin{eqnarray*}\omega^*=\sum_{i=1}^{m}\alpha_{i}^{*}y_ix_i\end{eqnarray*}\\b^* = y_j-\sum_{i=1}^{N}\alpha_i^*y_i(x_i\cdot x_j)

其中j使得 α∗j>0 \alpha_j^*>0

这样，就得到线性可分的支持向量机。