【图解例说机器学习】模型选择:偏差与方差 (Bias vs. Variance)
目录
- 一个例子:多项式回归中的阶数选择
- 防止过拟合
- 增加训练数据
- 正则化
- 偏差与方差
- 理论推导
- 偏差与方差的折中关系
- 附录
机器学习的过程大致分为三步:1)模型假设,比如我们假设模型是线性回归,还是多项式回归,以及其阶数的选择;2)误差函数定义,比如我们假设误差函数是均方误差,还是交叉熵;3)参数求解,比如使用正规方程,还是梯度下降等。
这篇文章主要讨论模型的选择问题,下面以多项式回归为例进行说明
一个例子:多项式回归中的阶数选择
在前面的文章【图解例说机器学习】线性回归中,我们定义了广义的线性回归模型,其表达式为:
y ^ = ω 0 + ∑ j = 1 M ω j ϕ j ( x ) = ω 0 + w T ϕ ( x ) (1) \hat y=\omega_0+\sum\limits_{j=1}^{M}\omega_j\phi_j(\mathrm x)=\omega_0+\mathrm w^{\mathrm T}\phi(\mathrm x)\tag{1} y^=ω0+j=1∑Mωjϕj(x)=ω0+wTϕ(x)(1)
当 D = 1 , ϕ j ( x ) = x j D=1,\phi_j(\mathrm x)=x^j D=1,ϕj(x)=xj时,公式(1)可以表示为:
y ^ = ω 0 + ω 1 x + ω 2 x 2 + ⋯ + ω M x M (2) \hat y=\omega_0+\omega_1x+\omega_2x^2+\cdots+\omega_Mx^M\tag{2} y^=ω0+ω1x+ω2x2+⋯+ωMxM(2)
此时,线性回归就变成了 M M M阶多项式回归。
当 M M M及误差函数给定时,我们就可以通过梯度下降法求解得到 w \mathrm w w。但是, M M M的选择对预测的结果影响较大。从公式可以看出 M M M越大,模型越复杂,其函数表达式集合包含了 M M M取值较小的情况。从这种角度来看, M M M取值越大越好。但是,一般来说训练数据较少,当 M M M取值较大时,复杂的模型会过度学习训练数据间的关系,导致其泛化能力较差。
这里我们通过一个实例来形象化 M M M对算法的影响。这里我们假设实际的函数表达式为
y = sin ( 2 π x ) + ϵ (3) y=\sin(2\pi x)+\epsilon\tag{3} y=sin(2πx)+ϵ(3)
其中, ϵ \epsilon ϵ是一个高斯误差值。通过公式(3)我们产生10个样例点 ( x i , y i ) (x_i,y_i) (xi,yi)。在给定不同 M M M值时,我们使用正规方程法或梯度下降法可以得到最佳的函数表达式。在这里,我们采用正规方程法 (见【图解例说机器学习】线性回归中公式(12)),得到最优参数:
w ˉ = [ ϕ ˉ T ( X ) ϕ ˉ ( X ) ] − 1 ϕ ˉ T ( X ) y (4) \mathrm{\bar w}=[\bar\phi^{\mathrm T}(\mathrm X)\bar\phi(\mathrm X)]^{-1}\bar\phi^{\mathrm T}(\mathrm X)\mathrm y\tag{4} wˉ=[ϕˉT(X)ϕˉ(X)]−1ϕˉT(X)y(4)
其中,这里的 ϕ ˉ T ( X ) \bar{\phi}^{\mathrm T}(\mathrm X) ϕˉT(X)根据公式(2)和【图解例说机器学习】线性回归中的公式(12)可得
ϕ ˉ ( X ) = { ϕ 0 ( x 1 ) ϕ 1 ( x 1 ) ⋯ ϕ M ( x 1 ) ϕ 0 ( x 2 ) ϕ 1 ( x 2 ) ⋯ ϕ M ( x 2 ) ⋮ ⋮ ⋯ ⋮ ϕ 0 ( x N ) ϕ 1 ( x N ) ⋯ ϕ M ( x N ) } = { 1 x 1 1 ⋯ x 1 M 1 x 2 1 ⋯ x 2 M ⋮ ⋮ ⋯ ⋮ 1 x N ⋯ x N M } (5) \bar\phi(\mathrm X)= \left\{\begin{matrix} \phi_0(\mathrm x_1) & \phi_1(\mathrm x_1) & \cdots & \phi_M(\mathrm x_1)\\ \phi_0(\mathrm x_2) & \phi_1(\mathrm x_2) & \cdots & \phi_M(\mathrm x_2)\\ \vdots & \vdots & \cdots &\vdots \\ \phi_0(\mathrm x_N) & \phi_1(\mathrm x_N) & \cdots & \phi_M(\mathrm x_N) \end{matrix} \right\}= \left\{\begin{matrix} 1 & \mathrm x_1^1 & \cdots & \mathrm x_1^{M}\\ 1 & \mathrm x_2^1 & \cdots & \mathrm x_2^{M}\\ \vdots & \vdots & \cdots &\vdots \\ 1 & \mathrm x_N & \cdots &\mathrm x_N^M \end{matrix} \right\}\tag{5} ϕˉ(X)=⎩⎪⎪⎪⎨⎪⎪⎪⎧ϕ0(x1)ϕ0(x2)⋮ϕ0(xN)ϕ1(x1)ϕ1(x2)⋮ϕ1(xN)⋯⋯⋯⋯ϕM(x1)ϕM(x2)⋮ϕM(xN)⎭⎪⎪⎪⎬⎪⎪⎪⎫=⎩⎪⎪⎪⎨⎪⎪⎪⎧11⋮1x11x21⋮xN⋯⋯⋯⋯x1Mx2M⋮xNM⎭⎪⎪⎪⎬⎪⎪⎪⎫(5)
利用正规方程法,即公式(5),我们可以得到如下 M M M取不同值时的函数表达式:
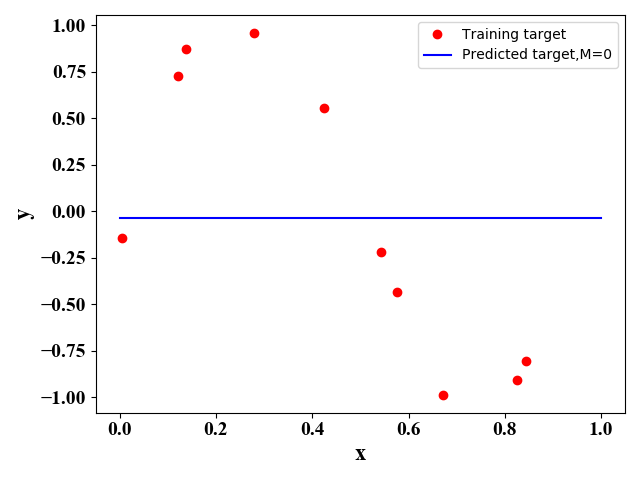 图1 图1
|
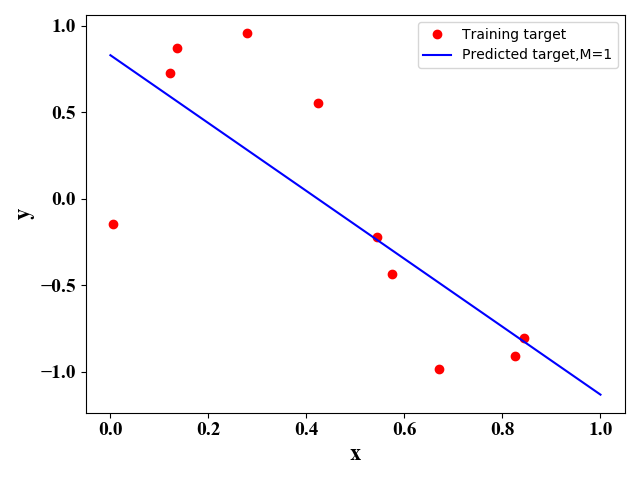 图2 图2
|
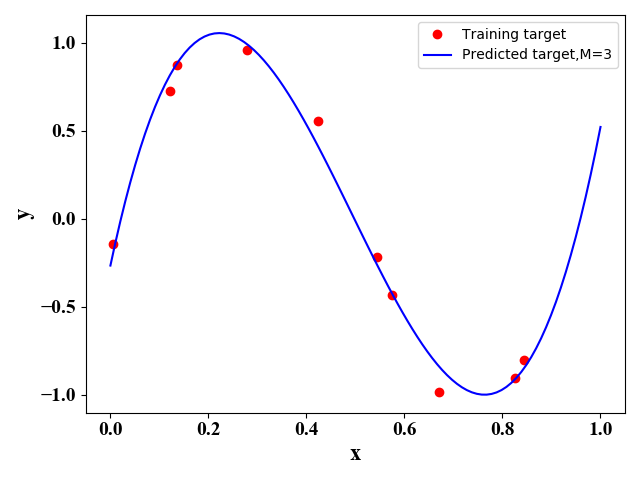 图3 图3
|
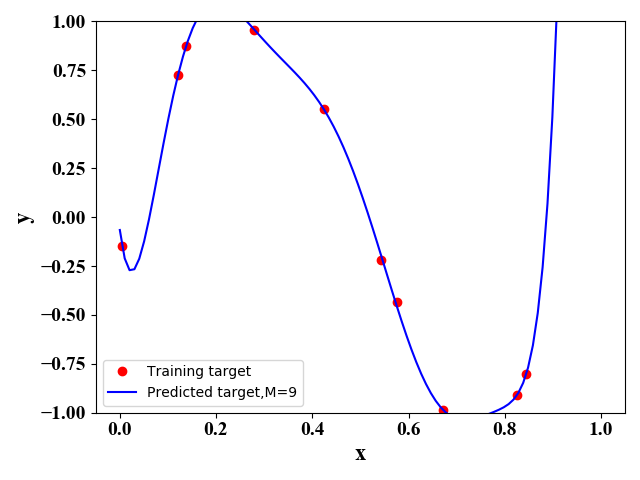 图4 图4
|
图1-图4表明,随着 M M M的增大,函数图像对训练样本的拟合越来越好,即训练误差越来越小。但是很明显图3的图像与原始的正弦函数图像最相似,即预测误差最小。 下表给出了图1-图4对应的最优的 w \mathrm w w 的取值:
| w | M = 0 M=0 M=0 | M = 1 M=1 M=1 | M = 3 M=3 M=3 | M = 9 M=9 M=9 |
|---|---|---|---|---|
| ω 0 \omega_0 ω0 | − 0.0379 -0.0379 −0.0379 | 0.8309 0.8309 0.8309 | − 0.2655 -0.2655 −0.2655 | − 6.5887 ∗ 1 0 − 2 -6.5887*10^{-2} −6.5887∗10−2 |
| ω 1 \omega_1 ω1 | − 1.9631 -1.9631 −1.9631 | 13.1817 13.1817 13.1817 | − 1.9234 ∗ 1 0 1 -1.9234*10^1 −1.9234∗101 | |
| ω 2 \omega_2 ω2 | − 38.3154 -38.3154 −38.3154 | 5.2109 ∗ 1 0 2 5.2109*10^2 5.2109∗102 | ||
| ω 3 \omega_3 ω3 | 25.9214 25.9214 25.9214 | − 3.8321 ∗ 1 0 3 -3.8321*10^3 −3.8321∗103 | ||
| ω 4 \omega_4 ω4 | 1.3080 ∗ 1 0 4 1.3080*10^4 1.3080∗104 | |||
| ω 5 \omega_5 ω5 | − 2.1917 ∗ 1 0 4 -2.1917*10^4 −2.1917∗104 | |||
| ω 6 \omega_6 ω6 | 1.2754 ∗ 1 0 4 1.2754*10^4 1.2754∗104 | |||
| ω 7 \omega_7 ω7 | 1.1027 ∗ 1 0 4 1.1027*10^4 1.1027∗104 | |||
| ω 8 \omega_8 ω8 | − 1.8864 ∗ 1 0 4 -1.8864*10^4 −1.8864∗104 | |||
| ω 9 \omega_9 ω9 | 7.2725 ∗ 1 0 3 7.2725*10^3 7.2725∗103 |
机器学习的目的就是选取最优的 M M M值,最小化预测误差。但是实际值中,预测误差是在算法之后才能得到的(不然的话,预测有什么用),我们都是通过验证误差来模拟预测误差。也就是说,我们一般把已经标记的数据集分为训练集和验证集,通过训练集来得到给定不同 M M M时最小验证误差,从而选择最佳的 M M M。图5和图6给出了 M M M取值不同情况下的训练误差和验证误差:
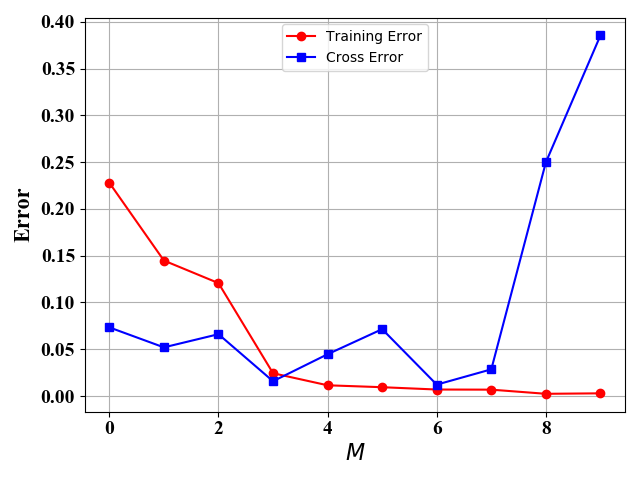 图5 10个训练样例 图5 10个训练样例
|
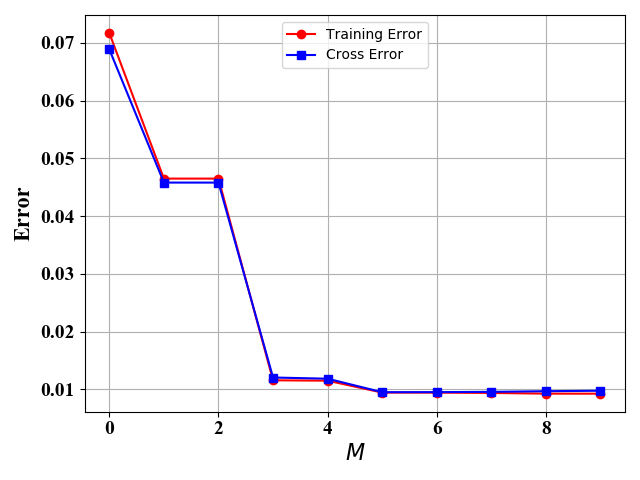 图6 100个训练样例 图6 100个训练样例
|
在图5和图6中,训练样例和验证样例都是由公式(3)给出,但是图5只有10个训练样例,图6有100个训练样例,验证样例都为100。从图中可知,训练误差都是随 M M M 增加而下降。图5中,当训练样例为10个时,此时我们可以选择 M = 3 M=3 M=3 或者 M = 6 M=6 M=6 得到较小的验证误差。当训练样例足够多时,如图6所示,此时 M M M越大,验证误差越好。
根据上述讨论,我们可以总结如下:
当训练样例较少时,我们需要选择合适的模型的复杂度,即这里的 M M M值;当训练样例较多时,我们选择的模型越复杂越好,即选择较大的 M M M值。
防止过拟合
当训练数据较少,而模型较为复杂时,容易出现过拟合。如在图1-图6中,只有 10 10 10 个训练数据,当 M = 9 M=9 M=9时,误差变大,这时出现过拟合现象。因此,我们可以通过增加训练数据和正则化来防止过拟合。
增加训练数据
图7和图8给出了,在 M = 9 M=9 M=9情况下,不同训练样例对函数表达式的模拟情况。可见,当训练样例较多时,得到的模型与原始模型(正选函数)更接近。
 图7 50个训练样例 图7 50个训练样例
|
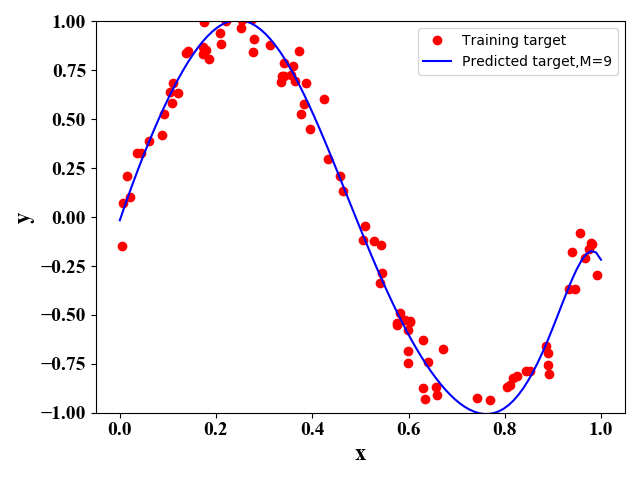 图8 100个训练样例 图8 100个训练样例
|
正则化
从上面的表格中可以看出,当过拟合时( M = 9 M=9 M=9),输入变量 x \mathrm x x的系数 w \mathrm{w} w的系数变得特别大.此时,当 x \mathrm{x} x变动十分小时,输出 y ^ \hat y y^也变得很大,这就导致了预测时误差变大。此时,我们可以对误差函数加入惩罚项,来限制 w \mathrm{w} w的取值:
E = ∑ i = 1 N ( y ^ i − y i ) 2 + λ 2 ∣ w ∣ 2 (6) E=\sum\limits_{i=1}^N{(\hat y_i-y_i)^2}+\frac{\lambda}{2}\lvert\mathrm{w}\rvert^2\tag{6} E=i=1∑N(y^i−yi)2+2λ∣w∣2(6)
公式(6)中的 λ \lambda λ可以自己调节来选取合适的值。
同样地,我们可以使用正规方程来使得新的误差函数(6)最小。此时的解析解可以表示为:
w ˉ = [ ϕ ˉ T ( X ) ϕ ˉ ( X ) + λ I 0 ] − 1 ϕ ˉ T ( X ) y (7) \mathrm{\bar w}=[\bar\phi^{\mathrm T}(\mathrm X)\bar\phi(\mathrm X)+\lambda\mathrm I_0]^{-1}\bar\phi^{\mathrm T}(\mathrm X)\mathrm y\tag{7} wˉ=[ϕˉT(X)ϕˉ(X)+λI0]−1ϕˉT(X)y(7)
其中 I 0 \mathrm I_0 I0是一个 ( M + 1 ) × ( M + 1 ) (M+1)\times(M+1) (M+1)×(M+1)的对角矩阵,且第一个对角元素为0(因为我们一般在正则项中不考虑 ω 0 \omega_0 ω0,见P10, PRML),其他对角元素为 1 1 1。
注意:公式(7)可以对 E E E求导,使其为零得到,这里就不详细推导。
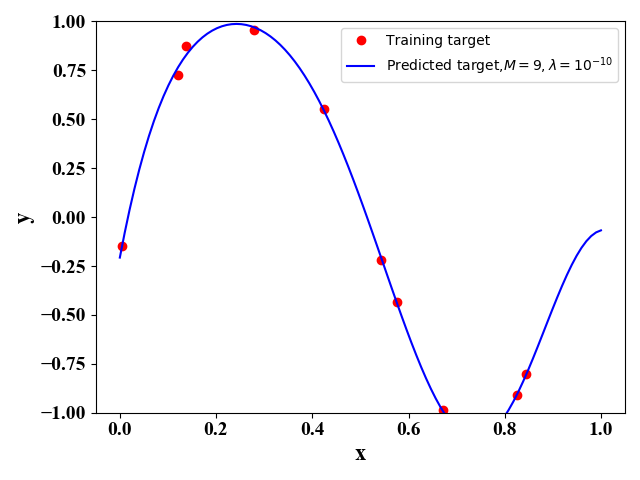 图9 图9
|
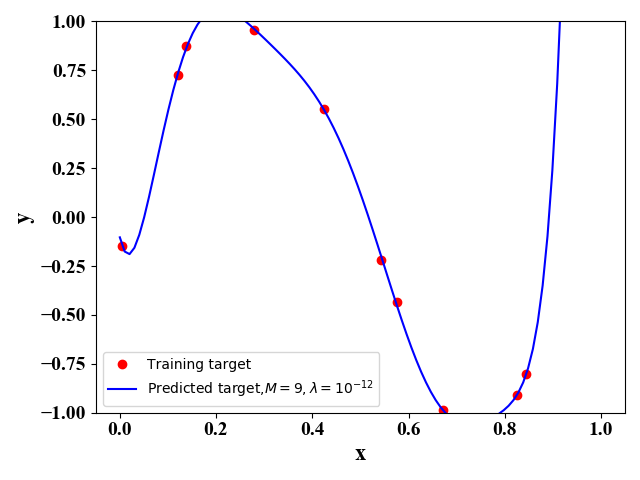 图10 图10
|
图9和图10给出了当测试样例为10, λ \lambda λ取不同值的函数拟合情况。可以看出, λ \lambda λ越小,对训练样例的拟合越好,即训练误差越小,但是此时图像与原始的正弦函数差别较大。当 λ = 0 \lambda=0 λ=0时,即不考虑正则化,此时对应的是图4。图9和图10说明,我们可以通过加入正则项来避免过拟合的情况。
偏差与方差
理论推导
机器学习的目的就是最小化误差。一般采用的误差,如线性回归的平方和误差,逻辑回归的交叉熵误差。这些误差都是假定训练样例的权重一样,但是实际中,每个样例出现的概率是不同的。因此,我们这里定义一个平均误差函数:
E [ E ] = ∫ ∫ E ( y ^ , y ) p ( x , y ) d x d y (8) \mathbb E[E]=\int\int E(\hat y,y)p(\mathrm x,y)d\mathrm xdy\tag{8} E[E]=∫∫E(y^,y)p(x,y)dxdy(8)
这里的 E ( y ^ , y ) E(\hat y,y) E(y^,y)就是我们常用的误差函数,如下:
E ( y ^ , y ) = ( y ^ i − y i ) 2 (9) E(\hat y, y)=(\hat y_i-y_i)^2\tag{9} E(y^,y)=(y^i−yi)2(9)
E ( y ^ , y ) = − [ y i log y ^ i + ( 1 − y i ) log ( 1 − y ^ i ) ] (10) E(\hat y, y)=-[y_i\log{\hat y_i}+(1-y_i)\log{(1-\hat y_i)}]\tag{10} E(y^,y)=−[yilogy^i+(1−yi)log(1−y^i)](10)
可见,公式(8)是一个广义的误差函数。这里我们平方和误差函数为例,将公式(9)带入公式(8)中,我们有
E [ E ] = ∫ ∫ ( y ^ − y ) 2 p ( x , y ) d x d y (11) \mathbb E[E]=\int\int (\hat y-y)^2p(\mathrm x,y)d\mathrm xdy\tag{11} E[E]=∫∫(y^−y)2p(x,y)dxdy(11)
通过求导,令导数为0,我们可以得到最佳的函数表达式:
∂ E ( E ) ∂ y ^ = 2 ∫ ( y ^ − y ) p ( x , y ) d y = 0 (12) \frac{\partial\mathbb E(E)}{\partial\hat y}=2\int(\hat y-y)p(\mathrm x,y)dy=0\tag{12} ∂y^∂E(E)=2∫(y^−y)p(x,y)dy=0(12)
y ^ = ∫ y p ( x , y ) d y p ( x ) = ∫ y p ( y ∣ x ) d y = E y [ y ∣ x ] = y ⋆ (13) \hat y=\frac{\int yp(\mathrm x,y)dy}{p(\mathrm x)}=\int yp(y\mid\mathrm x)dy=\mathbb E_y[y\mid\mathrm x]=y^\star\tag{13} y^=p(x)∫yp(x,y)dy=∫yp(y∣x)dy=Ey[y∣x]=y⋆(13)
根据公式(13)我们可以重写(11)
E ( E ) = ∫ ∫ ( y ^ − y ⋆ + y ⋆ − y ) 2 p ( x , y ) d x d y = ∫ ∫ [ ( y ^ − y ⋆ ) 2 + 2 ( y ^ − y ⋆ ) ( y ⋆ − y ) + ( y ⋆ − y ) 2 ] d x d y = ∫ ( y ^ − y ⋆ ) 2 p ( x ) d x + ∫ ( y ⋆ − y ) 2 p ( x ) d x (14) \begin{aligned} \mathbb E(E)&=\int\int(\hat y-y^\star+y^\star-y)^2p(\mathrm x,y)d\mathrm xdy\\ &=\int\int[(\hat y-y^\star)^2+2(\hat y-y^\star)(y^\star-y)+(y^\star-y)^2]d\mathrm xdy\\ &=\int(\hat y-y^\star)^2p(\mathrm x)d\mathrm x+\int(y^\star-y)^2p(\mathrm x)d\mathrm x\tag{14} \end{aligned} E(E)=∫∫(y^−y⋆+y⋆−y)2p(x,y)dxdy=∫∫[(y^−y⋆)2+2(y^−y⋆)(y⋆−y)+(y⋆−y)2]dxdy=∫(y^−y⋆)2p(x)dx+∫(y⋆−y)2p(x)dx(14)
公式(14)中的第二项与我们要求的函数表达式 y ^ \hat y y^没有关系。因此,当我们得到最优的函数表达式( y ^ = y ⋆ \hat y=y^\star y^=y⋆),即公式第一项为0,第二项即为我们得到的最小误差值。然而,由于训练数据有限(一般假定训练数据集为 D = { x i ∣ i = 1 , 2 , ⋯ , N } \mathcal D=\{\mathrm x_i\mid i=1,2,\cdots,N\} D={xi∣i=1,2,⋯,N}),得到最优解( y ^ = y ⋆ = E ( y ∣ x ) \hat y=y^\star=\mathbb E(y\mid\mathrm x) y^=y⋆=E(y∣x))一般是比较困难的。但我们有充足的训练数据 x \mathrm x x, 我们理论上可以得到条件期望 E ( y ∣ x ) = ∫ y p ( y ∣ x ) d y \mathbb E(y\mid\mathrm x)=\int yp(y\mid\mathrm x)dy E(y∣x)=∫yp(y∣x)dy, 也就是最优的函数表达式 y ^ \hat y y^。
真实的 y y y 与 x \mathrm x x的关系由 p ( x , y ) p(\mathrm x,y) p(x,y)决定,假定由 p ( x , y ) p(\mathrm x,y) p(x,y)产生很多不同训练数据集 D \mathcal D D 。对于每一个数据集 D \mathcal D D, 我们都能通过机器学习算法得到一个函数表达式 y ^ D \hat y_{\mathcal D} y^D。那么,我们需要在所有可能的训练数据集来评价 y ^ D \hat y_{\mathcal D} y^D的好坏,即我们需要计算 y ^ D \hat y_{\mathcal D} y^D在所以训练集上的平均误差。那么公式(14)可以写成:
E ( E ) = ∫ E D [ ( y ^ − y ⋆ ) 2 ] p ( x ) d x + ∫ ( y ⋆ − y ) 2 p ( x ) d x = ∫ { ( E D [ y ^ D ] − y ⋆ ) 2 + E D [ ( y ^ D − E D [ y ^ D ] ) 2 ] } p ( x ) d x + ∫ ( y ⋆ − y ) 2 p ( x ) d x = ∫ ( E D [ y ^ D ] − y ⋆ ) 2 p ( x ) d x ⏟ ( b i a s ) 2 + ∫ E D [ ( y ^ D − E D [ y ^ D ] ) 2 ] p ( x ) d x ⏟ v a r i a n c e + ∫ ( y ⋆ − y ) 2 p ( x ) d x ⏟ n o i s e (15) \begin{aligned} \mathbb E(E)&=\int\mathbb E_{\mathcal D}[(\hat y-y^\star)^2]p(\mathrm x)d\mathrm x+\int(y^\star-y)^2p(\mathrm x)d\mathrm x\\ &=\int\{(\mathbb E_{\mathcal D}[\hat y_{\mathcal D}]-y^\star)^2+\mathbb E_{\mathcal D}[(\hat y_{\mathcal D}-\mathbb E_{\mathcal D}[\hat y_{\mathcal D}])^2]\}p(\mathrm x)d\mathrm x+\int(y^\star-y)^2p(\mathrm x)d\mathrm x\\ &=\underbrace{\int(\mathbb E_{\mathcal D}[\hat y_{\mathcal D}]-y^\star)^2p(\mathrm x)d\mathrm x}_{(bias)^2}+\underbrace{\int\mathbb E_{\mathcal D}[(\hat y_{\mathcal D}-\mathbb E_{\mathcal D}[\hat y_{\mathcal D}])^2]p(\mathrm x)d\mathrm x}_{variance}+\underbrace{\int(y^\star-y)^2p(\mathrm x)d\mathrm x}_{noise}\tag{15} \end{aligned} E(E)=∫ED[(y^−y⋆)2]p(x)dx+∫(y⋆−y)2p(x)dx=∫{(ED[y^D]−y⋆)2+ED[(y^D−ED[y^D])2]}p(x)dx+∫(y⋆−y)2p(x)dx=(bias)2 ∫(ED[y^D]−y⋆)2p(x)dx+variance ∫ED[(y^D−ED[y^D])2]p(x)dx+noise ∫(y⋆−y)2p(x)dx(15)
可见,误差由bias (偏差),variance (方差),和noise (噪声)三部分组成。其中,bias和variance都和我们的模型选择 y ^ D \hat y_{\mathcal D} y^D 有关。第三项noise可以表示为 ∫ ( E D [ y ∣ x ] − y ) 2 p ( x ) d x \int(\mathbb E_{\mathcal D}[y\mid\mathrm x]-y)^2p(\mathrm x)d\mathrm x ∫(ED[y∣x]−y)2p(x)dx, 即可以看成是训练数据自身的特征: y y y的方差。对于公式(15),我们可以计算各部分值如下:
- E D [ y ^ D ] \mathbb E_{\mathcal D}[\hat y_{\mathcal D}] ED[y^D] 指的是对 y ^ \hat y y^在 L L L个数据集上求平均值,那么我们有:
E D [ y ^ D ( x ) ] = 1 L ∑ l = 1 L y ^ l ( x ) (16) \mathbb E_{\mathcal D}[\hat y_{\mathcal D}(\mathrm x)]=\frac{1}{L}\sum\limits_{l=1}^{L}\hat y_l(\mathrm x)\tag{16} ED[y^D(x)]=L1l=1∑Ly^l(x)(16) - 将公式(16)带入公式(15)中,我们有:
( b i a s ) 2 = 1 N ∑ i = 1 N { E D [ y ^ D ( x i ) ] − y ⋆ ( x i ) } 2 (17) (bias)^2=\frac{1}{N}\sum\limits_{i=1}^{N}\{\mathbb E_{\mathcal D}[\hat y_{\mathcal D}(\mathrm x_i)]-y^\star(\mathrm x_i)\}^2\tag{17} (bias)2=N1i=1∑N{ED[y^D(xi)]−y⋆(xi)}2(17)
v a r i a n c e = 1 N ∑ i = 1 N 1 L ∑ l = 1 L { y ^ l ( x i ) − E D [ y ^ D ( x i ) ] } 2 (18) variance=\frac{1}{N}\sum\limits_{i=1}^{N}\frac{1}{L}\sum\limits_{l=1}^{L}\{\hat y_l(\mathrm x_i)-\mathbb E_{\mathcal D}[\hat y_{\mathcal D}(\mathrm x_i)]\}^2\tag{18} variance=N1i=1∑NL1l=1∑L{y^l(xi)−ED[y^D(xi)]}2(18)
注意:在计算公式(15)的积分项 ∫ p ( x ) d x \int p(\mathrm x)d\mathrm x ∫p(x)dx 时,我们采用的是将所有的 x \mathrm x x 所得到的结果加和求平均,即 ∑ / N \sum/N ∑/N。因为这里我们假定所有训练样例都是均匀采样的。
一般来说,模型( y ^ ( x ) \hat y(\mathrm x) y^(x))越复杂,偏差越小,方差越大。因为模型越复杂,对于我们训练样例集的每一个样例 x i \mathrm x_i xi的拟合较好,也就是说 y ^ l ( x i ) \hat y_l(\mathrm x_i) y^l(xi)与 y ⋆ ( x i ) y^\star(\mathrm x_i) y⋆(xi)比较接近,即公式(17)的值较小(偏差较小);而此时,不同训练样例集产生的 y ^ l ( x i ) \hat y_l(\mathrm x_i) y^l(xi)之间值存在较大波动,即公式(18)的值较大(方差较大)。换句话说,公式(17),即偏差,针对的是 y ^ l ( x i ) \hat y_l(\mathrm x_i) y^l(xi)与真实函数 y ⋆ ( x i ) y^\star(\mathrm x_i) y⋆(xi)之间的误差;而公式(18),即方差,针对的是不同数据集所得到的函数 y ^ l ( x i ) \hat y_l(\mathrm x_i) y^l(xi)之间的误差。
偏差与方差的折中关系
我们通过函数表达式(3)来产生 L = 100 L=100 L=100个训练数据集,每个数据集包含 N = 30 N=30 N=30个训练样例。那么此时,我们有 y ⋆ = sin ( 2 π x ) y^\star=\sin(2\pi\mathrm x) y⋆=sin(2πx)且此时公式(15)的第三项noise可以由 ϵ \epsilon ϵ的分布求出。我们假定用 M = 9 M=9 M=9的多项式函数(2)来作为 y ^ \hat y y^的表达式。当正则项的系数分别为 λ = 1 0 − 3 , 1 0 − 12 \lambda=10^{-3},10^{-12} λ=10−3,10−12时,我们可以分别得到图11-12,和图13-14:
 图11 图11
|
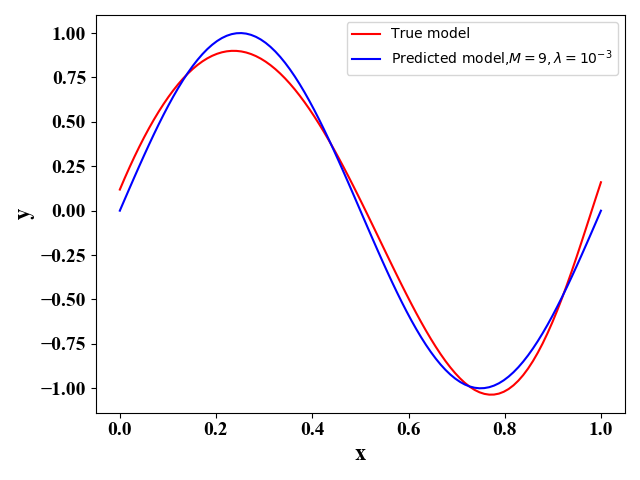 图12 图12
|
 图13 图13
|
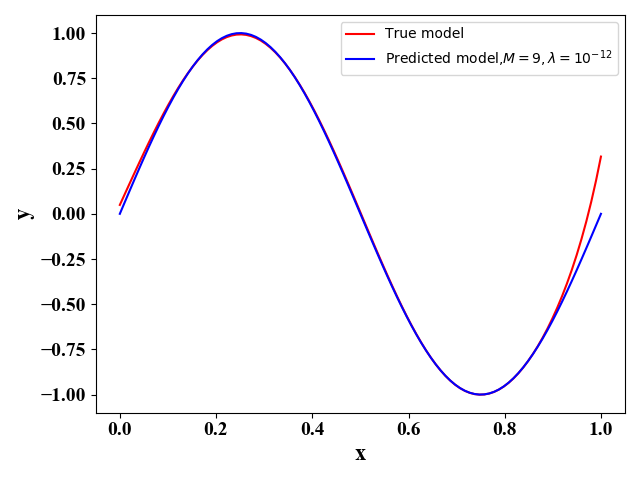 图14 图14
|
图11和图13表示的是在这100个训练数据集下 y ^ \hat y y^关于 x \mathrm x x 的函数图像。图12和图14表示的是在左图100条函数取平均情况下的函数图像,其中红色曲线是我们最优的函数 y ⋆ y^\star y⋆。左图可以反映各个函数表达式间的差别,公式(18), 即方差,右图表示的是预测函数 E D [ y ^ D ] \mathbb E_{\mathcal D}[\hat y_{\mathcal D}] ED[y^D]与最优函数 y ⋆ y^\star y⋆的差别,公式(17),即偏差。通过图11-14,我们可以看出偏差与方差的折中关系。
经过上面的分析,我们可以看出误差主要由偏差、方差和噪声组成,并从中可以看出模型的选择(e.g.,这里 M , λ M,\lambda M,λ的选择)对误差的本质影响,从而指导模型的选择。由公式(16)-(18)可以看出,误差的分析是建立在很多数据集上的统计平均值。但是在实际中,训练数据集很少。当我们有很多的数据集,我们可以把它们看出一个大的数据集,这样我们就可以防止过拟合现象(见图7-8)。
附录
下面我们给出图1-图14的python源代码。注意,在运行代码时,可以自行调整自变量 M , N , λ M,N,\lambda M,N,λ等。
图1-图4:
# -*- coding: utf-8 -*-
# @Time : 2020/4/16 23:40
# @Author : tengweitwimport numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import datasets# Set the format of labels
def LabelFormat(plt):ax = plt.gca()plt.tick_params(labelsize=14)labels = ax.get_xticklabels() + ax.get_yticklabels()[label.set_fontname('Times New Roman') for label in labels]font = {'family': 'Times New Roman','weight': 'normal','size': 16,}return fontdef Polynomial_regression_normal_equation(train_data, train_target, test_data, test_target):# the 1st column is 1 i.e., x_0=1X = np.ones([np.size(train_data, 0), 1])X_test = np.ones([np.size(test_data, 0), 1])# Here to change M !!!!!!!M = 2for i in range(1, M + 1):temp = train_data ** itemp_test = test_data ** iX = np.concatenate((X, temp), axis=1)X_test = np.concatenate((X_test, temp_test), axis=1)# X is a 10*M-dim matrix# Normal equationw_bar = np.matmul(np.linalg.pinv(np.matmul(X.T, X)), np.matmul(X.T, train_target))# Training Errory_predict_train = np.matmul(X, w_bar)E_train = np.linalg.norm(y_predict_train - train_target) / len(y_predict_train)# Predictingy_predict_test = np.matmul(X_test, w_bar)# Prediction ErrorE_test = np.linalg.norm(y_predict_test - test_target) / len(y_predict_test)return y_predict_test, E_train, E_testif __name__ == '__main__':# keep the same random training dataseed_num = 100np.random.seed(seed_num)# 10 training datatrain_data = np.random.uniform(0, 1, (10, 1))train_data = np.sort(train_data, axis=0)np.random.seed(seed_num)train_target = np.sin(2 * np.pi * train_data) + 0.1 * np.random.randn(10, 1)test_data = np.linspace(0, 1, 100).reshape(100, 1)np.random.seed(seed_num)test_target = np.sin(2 * np.pi * test_data) + 0.01 * np.random.randn(100, 1)y_predict_test, E_train, E_test = Polynomial_regression_normal_equation(train_data, train_target, test_data,test_target)plt.figure()plt.plot(train_data, train_target, 'ro')plt.plot(test_data, y_predict_test, 'b-')# Set the labelsfont = LabelFormat(plt)plt.xlabel('x', font)plt.ylabel('y', font)plt.legend(['Training target', 'Predicted target,M=2'])plt.ylim([-1, 1])plt.show()图5-图8:
# -*- coding: utf-8 -*-
# @Time : 2020/4/18 11:56
# @Author : tengweitwimport numpy as np
import matplotlib.pyplot as plt# Set the format of labels
def LabelFormat(plt):ax = plt.gca()plt.tick_params(labelsize=14)labels = ax.get_xticklabels() + ax.get_yticklabels()[label.set_fontname('Times New Roman') for label in labels]font = {'family': 'Times New Roman','weight': 'normal','size': 16,}return fontdef Polynomial_regression_normal_equation(train_data, train_target, cv_data, cv_target,test_data,M):# the 1st column is 1 i.e., x_0=1X = np.ones([np.size(train_data, 0), 1])X_cv = np.ones([np.size(cv_data, 0), 1])X_test = np.ones([np.size(test_data, 0), 1])for i in range(1, M + 1):temp = train_data ** itemp_cv = cv_data ** itemp_test = test_data ** iX = np.concatenate((X, temp), axis=1)X_cv = np.concatenate((X_cv, temp_cv), axis=1)X_test = np.concatenate((X_test, temp_test), axis=1)# X is a 10*M-dim matrix# Normal equationw_bar = np.matmul(np.linalg.pinv(np.matmul(X.T, X)), np.matmul(X.T, train_target))# Training Errory_predict_train = np.matmul(X, w_bar)E_train = np.linalg.norm(y_predict_train - train_target) / len(y_predict_train)# cross validationy_predict_cv = np.matmul(X_cv, w_bar)# predictiony_predict_test=np.matmul(X_test, w_bar)# Prediction ErrorE_cv = np.linalg.norm(y_predict_cv - cv_target) / len(y_predict_cv)print(w_bar)return y_predict_test, y_predict_cv, E_train, E_cvif __name__ == '__main__':# keep the same random training dataseed_num = 100np.random.seed(seed_num)# training datanum_training=50train_data = np.random.uniform(0, 1, (num_training, 1))train_data = np.sort(train_data, axis=0)np.random.seed(seed_num)train_target = np.sin(2 * np.pi * train_data) + 0.1 * np.random.randn(num_training, 1)# 100 cross validation datanum_cv=100cv_data = np.random.uniform(0, 1, (num_cv, 1))cv_data = np.sort(cv_data, axis=0)np.random.seed(seed_num)cv_target = np.sin(2 * np.pi * cv_data) + 0.1 * np.random.randn(num_cv, 1)# testing datatest_data = np.linspace(0, 1, 100).reshape(100, 1)M=9+1E_train=np.zeros((M,1))E_cv=np.zeros((M,1))# change Mfor i in range(M):y_predict_test,y_predict_cv, E_train[i], E_cv[i] = Polynomial_regression_normal_equation(train_data, train_target, cv_data, cv_target,test_data, i)plt.figure()plt.plot(E_train, 'r-o')plt.plot(E_cv,'b-s')# Set the labelsfont = LabelFormat(plt)plt.xlabel('$M$', font)plt.ylabel('Error', font)plt.legend(['Training Error', 'Cross Error'],loc='upper center')plt.grid()plt.show()plt.figure()plt.plot(train_data, train_target, 'ro')plt.plot(test_data, y_predict_test, 'b-')# Set the labelsfont = LabelFormat(plt)plt.xlabel('x', font)plt.ylabel('y', font)plt.legend(['Training target', 'Predicted target,M=9'])plt.ylim([-1, 1])plt.show()
图9-图10:
# -*- coding: utf-8 -*-
# @Time : 2020/4/18 23:12
# @Author : tengweitwimport numpy as np
import matplotlib.pyplot as plt# Set the format of labels
def LabelFormat(plt):ax = plt.gca()plt.tick_params(labelsize=14)labels = ax.get_xticklabels() + ax.get_yticklabels()[label.set_fontname('Times New Roman') for label in labels]font = {'family': 'Times New Roman','weight': 'normal','size': 16,}return fontdef Polynomial_regression_normal_equation(train_data, train_target, cv_data, cv_target,test_data,M):# the 1st column is 1 i.e., x_0=1X = np.ones([np.size(train_data, 0), 1])X_cv = np.ones([np.size(cv_data, 0), 1])X_test = np.ones([np.size(test_data, 0), 1])# Here to change lambdaLambda=1e-12I0= np.eye(M+1)I0[0]=0for i in range(1, M + 1):temp = train_data ** itemp_cv = cv_data ** itemp_test = test_data ** iX = np.concatenate((X, temp), axis=1)X_cv = np.concatenate((X_cv, temp_cv), axis=1)X_test = np.concatenate((X_test, temp_test), axis=1)# X is a 10*M-dim matrix# Normal equationw_bar = np.matmul(np.linalg.pinv(np.matmul(X.T, X)+Lambda*I0), np.matmul(X.T, train_target))# Training Errory_predict_train = np.matmul(X, w_bar)E_train = np.linalg.norm(y_predict_train - train_target) / len(y_predict_train)# cross validationy_predict_cv = np.matmul(X_cv, w_bar)# predictiony_predict_test=np.matmul(X_test, w_bar)# Prediction ErrorE_cv = np.linalg.norm(y_predict_cv - cv_target) / len(y_predict_cv)print(w_bar)return y_predict_test, y_predict_cv, E_train, E_cvif __name__ == '__main__':# keep the same random training dataseed_num = 100np.random.seed(seed_num)# training datanum_training=10train_data = np.random.uniform(0, 1, (num_training, 1))train_data = np.sort(train_data, axis=0)np.random.seed(seed_num)train_target = np.sin(2 * np.pi * train_data) + 0.1 * np.random.randn(num_training, 1)# 100 cross validation datanum_cv=100cv_data = np.random.uniform(0, 1, (num_cv, 1))cv_data = np.sort(cv_data, axis=0)np.random.seed(seed_num)cv_target = np.sin(2 * np.pi * cv_data) + 0.1 * np.random.randn(num_cv, 1)# testing datatest_data = np.linspace(0, 1, 100).reshape(100, 1)M=9y_predict_test,y_predict_cv, E_train, E_cv = Polynomial_regression_normal_equation(train_data, train_target, cv_data, cv_target,test_data, M)plt.figure()plt.plot(train_data, train_target, 'ro')plt.plot(test_data, y_predict_test, 'b-')# Set the labelsfont = LabelFormat(plt)plt.xlabel('x', font)plt.ylabel('y', font)plt.legend(['Training target', 'Predicted target,$M=9,\lambda=10^{-12}$'])plt.ylim([-1, 1])plt.show()
图11-图14:
# -*- coding: utf-8 -*-
# @Time : 2020/4/20 10:46
# @Author : tengweitwimport numpy as np
import matplotlib.pyplot as plt# Set the format of labels
def LabelFormat(plt):ax = plt.gca()plt.tick_params(labelsize=14)labels = ax.get_xticklabels() + ax.get_yticklabels()[label.set_fontname('Times New Roman') for label in labels]font = {'family': 'Times New Roman','weight': 'normal','size': 16,}return fontdef Polynomial_regression_normal_equation(train_data, train_target,test_data,M):# the 1st column is 1 i.e., x_0=1X = np.ones([np.size(train_data, 0), 1])X_test = np.ones([np.size(test_data, 0), 1])# Here to change lambdaLambda=1e-8I0= np.eye(M+1)I0[0]=0for i in range(1, M + 1):temp = train_data ** itemp_test = test_data ** iX = np.concatenate((X, temp), axis=1)X_test = np.concatenate((X_test, temp_test), axis=1)# X is a 10*M-dim matrix# Normal equationw_bar = np.matmul(np.linalg.pinv(np.matmul(X.T, X)+Lambda*I0), np.matmul(X.T, train_target))# Training Errory_predict_train = np.matmul(X, w_bar)E_train = np.linalg.norm(y_predict_train - train_target) / len(y_predict_train)# predictiony_predict_test=np.matmul(X_test, w_bar)# Prediction Errorreturn y_predict_test, E_trainif __name__ == '__main__':# L is the number of training data setsL=100# number of each training dataN=30plt.figure()# For L training datasetsfor l in range(L):train_data = np.random.uniform(0, 1, (N, 1))train_data = np.sort(train_data, axis=0)train_target = np.sin(2 * np.pi * train_data) + 0.1* np.random.randn(N, 1)# testing datatest_data = np.linspace(0, 1, 100).reshape(100, 1)M=9y_predict_test, E_train = Polynomial_regression_normal_equation(train_data, train_target, test_data, M)if l==0:predict_target=y_predict_testelse:predict_target=np.hstack((y_predict_test,predict_target))# plt.plot(train_data, train_target, 'ro')plt.plot(test_data, y_predict_test, 'b-')# Set the labelsfont = LabelFormat(plt)plt.xlabel('x', font)plt.ylabel('y', font)plt.legend([ 'Predicted target,$M=9,\lambda=10^{-3}$'])plt.ylim(-1,1)plt.show()predict_target_avg=np.mean(predict_target,axis=1)plt.figure()plt.plot(test_data,predict_target_avg,'r-')test_target = np.sin(2 * np.pi * test_data)plt.plot(test_data,test_target,'b-')# Set the labelsfont = LabelFormat(plt)plt.xlabel('x', font)plt.ylabel('y', font)plt.legend(['True model', 'Predicted model,$M=9,\lambda=10^{-3}$'])plt.show()
【图解例说机器学习】模型选择:偏差与方差 (Bias vs. Variance)相关推荐
- 偏差和方差(bias and variance)
偏差和方差 什么是偏差和方差 偏差和方差的评价指标 偏差与方差的平衡 Reference 在机器学习中,我们每次解决问题从建立模型,确定准则,选择算法都不可避免地会受到偏差和方差的困扰,那么什么是偏差 ...
- 吴恩达机器学习作业5.偏差和方差
机器学习作业 5 - 偏差和方差 import numpy as np import scipy.io as sio import scipy.optimize as opt import panda ...
- 模型的偏差与方差的理解
本文转载于http://blog.csdn.net/xmu_jupiter/article/details/47314927 版权声明:本文为博主原创文章,欢迎转载,但请注明出处~ 目录(?)[+] ...
- 机器学习中的偏差和方差是什么?
机器学习中的偏差和方差是什么? 机器学习全部是关于给定输入数据(X)和给定输出数据(Y),然后去寻找一个最佳映射函数(F),这个映射函数通常也被叫做目标函数. 任何机器学习算法的预测误差可以分解为三部 ...
- 吴恩达机器学习课后作业——偏差和方差
1.写在前面 吴恩达机器学习的课后作业及数据可以在coursera平台上进行下载,只要注册一下就可以添加课程了.所以这里就不写题目和数据了,有需要的小伙伴自行去下载就可以了. 作业及数据下载网址:吴恩 ...
- 只能选择分卷文件的第一部分。_为机器学习模型选择正确的度量评估(第一部分)...
作者:Alvira Swalin 编译:ronghuaiyang 导读 对不同的应用场景,需要不同的模型,对于不同的模型,需要不同的度量评估方式.本系列的第一部分主要关注回归的度量 在后现代主义的世界 ...
- 机器学习 | 模型选择
文章目录 1. 模型验证 1.1 错误的模型验证方法 1.2 正确的模型验证方法 1.2.1 留出集 1.2.2 交叉验证 1.2.3 K折交叉验证 1.2.4 留一法 LOO 2. 偏差-方差 2. ...
- 机器学习模型 知乎_机器学习-模型选择与评价
交叉验证 首先选择模型最简单的方法就是,利用每一种机器学习算法(逻辑回归.SVM.线性回归等)计算训练集的损失值,然后选择其中损失值最小的模型,但是这样是不合理的,因为当训练集不够.特征过多时容易过拟 ...
- 转载:理解机器学习中的偏差与方差
学习算法的预测误差, 或者说泛化误差(generalization error)可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise). 在估计学习算法性能的过程中, ...
最新文章
- openstack 之 使用ansible安装部署试验
- LeetCode-461. 汉明距离(python3)
- RStudio-Desktop与RStudio-Server的启动方式
- Android开发之ANR原因分析
- cstring判断是否包含子串_最长子串-滑动窗口
- kettle 只有一个输入记录期待设置变量并且至少已经收到2个变量._OPNET学习笔记2...
- Mr.J--俄罗斯方块实现(框架)
- Python自带又好用的代码调试工具Pdb学习笔记
- Ubuntu 携手初创企业用代码开拓物联网
- android仿美丽说登录拖拽Layout
- jenkins+maven+svn+npm自动发布部署实践
- c++ 位运算 和 掩码
- eda交通灯控制器波形输入_交通灯控制器课程设计.doc
- 简单的C语言顺序结构例题介绍
- Ubuntu 10.10 无线网络已经禁用” “wiress is disabled” 解决方法
- 一个三流学校程序员的奋斗!(转)
- 电大学位计算机考试题库,电大学位英语跟考试题库一模一样.doc
- 使用C语言实现杨辉三角
- 飞猪、去哪儿网被列入大数据“杀熟”名单,超50%的人遭遇过被“杀熟”
- 微信小程序读取nfc获取Ndef写入的数据
