0 文章小节分类

相关线代启示录
对Laplancian Matrix的基础理解
对经典文章《Normalized Cuts and Image Segmentation》中的normalised cut algorithm部分做详细的个人理解与阐述

1. 相关线代启示录

1.1 特征值与特征向量部分：

https://blog.csdn.net/qq_38382642/article/details/103553825

1.2 二次型

通过矩阵来研究二次函数（方程），这就是线性代数中二次型的重点。所以我们可以通过二次函数来理解二次型。

1.2.1 二次函数的一个特点

给一元二次方程增加一次项，是不会改变二次函数的形状的：

当然了增加常数项更不会改变二次函数的形状。

1.2.2 二次方程

下面是一个二元二次方程：

给它增加一次项也不会改变形状，只是看上去有些伸缩：

1.2.3 小结论

对于二次方程或二次函数，增加一次项或常数项，不会改变其形状。形状，意味着函数的变化规律。

1.3 通过矩阵来研究二次函数

通过上面的观察可以知道，二次函数或二次方程，最重要的是二次项。

1.3.1 二次型矩阵

实际上我们可以通过矩阵来表示二次型：

更一般的情形：

写成更线代的形式：

所以可以总结得到如下对应关系：

1.3.2 对上述矩阵分解观察

对于方阵，因为没有维度的改变，所以就没有投影这个运动了，只有旋转和拉伸

把这个矩阵进行特征值分解(特征值分解实际上就是把运动分解了) (注意要正交）对于二次型矩阵，都是对称矩阵，所以特征值分解总可以得到正交矩阵与对角矩阵。所以只需要保留拉伸部分，就相当于把二次型矩阵 $A$扶正了，所以，用二次型矩阵进行**规范化**是非常轻松的事情。

1.4 对二次型的n维实向量x\rm xx的讨论

1.4.1 这种二次型是一个实函数，要有"整体视角"

令 A=[aij]A=[a_{ij}]A=[aij] 为一个 n×nn\times nn×n 阶实矩阵，x=[x1⋮xn]\mathbf{x}=\begin{bmatrix} x_1\\ \vdots\\ x_n \end{bmatrix}x=⎣⎢⎡x1⋮xn⎦⎥⎤ 为 nnn 维实向量，具有以下形式的实函数称为二次型 (quadratic form)：
f(x)=xTAxf(\mathbf{x})=\mathbf{x}^TA\mathbf{x}f(x)=xTAx

请注意，二次型 xTAx\mathbf{x}^TA\mathbf{x}xTAx 是一个纯量。任意二次型 xTAx\mathbf{x}^TA\mathbf{x}xTAx 都可以转换为等价的 xTBx\mathbf{x}^TB\mathbf{x}xTBx，其中 BBB 是一个实对称矩阵。利用一点运算技巧改写矩阵乘法公式可得:

正定矩阵的概念建立于二次型之上。若 AAA 是一个实对称矩阵且任一 x≠0\mathbf{x}\neq\mathbf{0}x=0 满足 xTAx>0\mathbf{x}^TA\mathbf{x}>0xTAx>0我们称 AAA是正定的，详见“正定矩阵”。因此讨论仅具对称性的二次型已足够应付一般的问题，这与我们习惯将对称性纳入正定的定义其道理是相同的。

1.4.2 分析二次型函数的最值问题

既然我们已经认为二次型是一个“自变量是n维实向量x\rm xx”的函数，那么随着x\rm xx的变化，二次型的值域也是不断变化。

对于矩阵而言，特征值和特征向量是线性代数分析矩阵结构与线性变换最重要的概念。二次型的最大化 (或最小化) 问题是特征值和特征向量的一个典型应用。设 A 是实对称矩阵，考虑此问题：

最大化 xTAx，x\mathbf{x}^TA\mathbf{x}，\mathbf{x}xTAx，x 满足 ∥x∥2=xTx=1\Vert\mathbf{x}\Vert^2=\mathbf{x}^T\mathbf{x}=1∥x∥2=xTx=1。

求解这个约束最佳化 (constrained optimization) 问题的传统方法是引入 Lagrangian 函数 (见“Lagrange 乘数法”)：
L(x,λ)≡xTAx−λ(xTx−1)L(\mathbf{x},\lambda)\equiv\mathbf{x}^TA\mathbf{x}-\lambda(\mathbf{x}^T\mathbf{x}-1)L(x,λ)≡xTAx−λ(xTx−1)产生极值的必要条件是 L 对 x\mathbf{x}x 的各元的一次偏导数都等于零，亦即 x\mathbf{x}x 是 LLL 的一个驻点 (参见“最佳化理论与正定矩阵”)。因为 AT=AA^T=AAT=A，易得：
0=∇xL=2(Ax−λx)\mathbf{0}=\nabla_{\mathbf{x}}L=2(A\mathbf{x}-\lambda\mathbf{x})0=∇xL=2(Ax−λx)

单位向量 (unit vector) x\mathbf{x}x 要使xTAx\mathbf{x}^TA\mathbf{x}xTAx 最大化的必要条件是满足特征方程式 Ax=λxA\mathbf{x}=\lambda\mathbf{x}Ax=λx，所以对二次型中的AxA\mathbf{x}Ax，正好有一个A，代入特征方程式可得

xTAx=xT(λx)=λ∥x∥2=λ\mathbf{x}^TA\mathbf{x}=\mathbf{x}^T(\lambda\mathbf{x})=\lambda\Vert\mathbf{x}\Vert^2=\lambdaxTAx=xT(λx)=λ∥x∥2=λ

实对称矩阵的特征值必为实数，因此使二次型最大化的向量 x\mathbf{x}x 正是对应最大特征值的特征向量。

另一方面，我们也可以直接利用实对称矩阵是正交可对角化此性质来分解二次型。
设 A=QΛQTA=Q\Lambda Q^{T}A=QΛQT，其中 QQQ是正交特征向量矩阵，QT=Q−1Q^T=Q^{-1}QT=Q−1，Λ=diag(λ1,…,λn)\Lambda=diag(\lambda_1,\ldots,\lambda_n)Λ=diag(λ1,…,λn)是主对角特征值矩阵。令 y=QTx\mathbf{y}=Q^{T}\mathbf{x}y=QTx，二次型可用主对角分解化简为：
xTAx=xTQλQTx=yTΛy=λ1y12+λ2y22+⋯+λnyn2。\mathbf{x}^TA\mathbf{x}=\mathbf{x}^TQ\lambda Q^{T}\mathbf{x}=\mathbf{y}^T\Lambda\mathbf{y}=\lambda_1y_1^2+\lambda_2y_2^2+\cdots+\lambda_ny_n^2。xTAx=xTQλQTx=yTΛy=λ1y12+λ2y22+⋯+λnyn2。因为 QQQ 是正交矩阵，∥y∥=∥QTx∥=∥x∥=1\Vert\mathbf{y}\Vert=\Vert Q^T\mathbf{x}\Vert=\Vert\mathbf{x}\Vert=1∥y∥=∥QTx∥=∥x∥=1 (见“特殊矩阵 (3)：么正矩阵（酉矩阵）”)，故可推论 yTΛy\mathbf{y}^T\Lambda\mathbf{y}yTΛy 的最大值即为 A 的最大特征值。

2. 对Laplancian Matrix的基础理解

2.1 Laplancian Matrix的定义

拉普拉斯矩阵的定义为：L=D−WL=D-WL=D−W其中，DDD是图的度矩阵，WWW是图的邻接矩阵。所以研究拉普拉斯矩阵实际表示的物理意义之前，需要先验一下图相关矩阵

2.1.1 简单介绍三种矩阵

我们先回顾图论的一些基本词。图 G=(V,E)G=(V, E)G=(V,E) 包含二类组成元件：顶点 (vertex) 集合 V={v1,v2,…,vn}V=\{v_1,v_2,\ldots,v_n\}V={v1,v2,…,vn} 与边 (edge) 集合 EEE，∣V∣\vert V\vert∣V∣ 与 ∣E∣\vert E\vert∣E∣ 分别表示顶点数与边的总数。边集合 EEE 中每个边由一对相异的顶点所定义，表示为 e={x,y}e=\{x,y\}e={x,y}，我们称顶点 xxx 和顶点 yyy 邻接 (adjacent)，并称顶点 xxx 和 yyy 与边 eee 有关联 (incident)。如果两个顶点存在不对称关系——例如，公司 x 是公司 y 的买主，连接 x 和 y 的边 {x,y}\{x,y\}{x,y} 具有方向性，称为有向边 (directed edge)，包含有向边的图称为有向图 (directed graph)。为了与无向边区别，我们将有向边记为 e=(x,y)e=(x,y)e=(x,y)（或者e={x,y}e=\{x,y\}e={x,y}），其中 x 是有向边 eee 的初始顶点，y 是终止顶点。本文仅考虑简单图，也就是说顶点与其自身不存在连接边，且二邻接顶点仅有一边。

W 邻接矩阵

用aija_{ij}aij表示顶点viv_ivi与顶点vjv_jvj之间的边数，可能取值为0,1,2,…，称所得矩阵A=A(G)=(aij)n×nA=A(G)=(a_{ij})_{n×n}A=A(G)=(aij)n×n为图GGG的邻接矩阵
*类似地，有向图DDD的邻接矩阵$A(D)=(a_{ij})_{n×n}, aija_{ij}aij表示从始点viv_ivi到终点vjv_jvj的有向边的条数，其中viv_ivi和vjv_jvj为DDD的顶点

举例：家庭成员5人，即∣V∣=5|V|=5∣V∣=5

邻接矩阵就是A=[0110000001010100100010100]A=\begin{bmatrix} 0&1&1&0&0\\ 0&0&0&0&1\\ 0&1&0&1&0\\ 0&1&0&0&0\\ 1&0&1&0&0 \end{bmatrix}A=⎣⎢⎢⎢⎢⎡0000110110100010010001000⎦⎥⎥⎥⎥⎤

D 度矩阵

将邻接矩阵各行元素相加求和，对应值作为对角线元素，所得到的矩阵成为度矩阵DDD,度矩阵中的第iii个对角线元素did_idi就代表与节点iii的连接的点的边数（对于有向图，为权值之和，此时di:=∑jωijd_i:=\sum_j\omega_{ij}di:=∑jωij）

度矩阵表示成D，是一个对角矩阵，对角线的元素则是每个节点所带的连接边的权重和（dij=∑kωikd_{ij}=\sum_k\omega_{ik}dij=∑kωik）

C 关联矩阵

弄清邻接矩阵和关联矩阵对接下来的LM理解是十分重要的：我个人的理解是前者无向图而后者为有向图：
令 G=(V,E)G=(V,E)G=(V,E) 为一个有向图，其中 V={v1,…,vn}V=\{v_1,\ldots,v_n\}V={v1,…,vn} 是顶点集合，E={e1,…,em}E=\{e_1,\ldots,e_m\}E={e1,…,em} 是有向边集合。我们以 ∣V∣\vert V\vert∣V∣ 和 ∣E∣\vert E\vert∣E∣ 分别表示顶点和边的总数，即 ∣V∣=n\vert V\vert=n∣V∣=n，∣E∣=m\vert E\vert=m∣E∣=m。有序对 ei=(vj,vk)e_i=(v_j,v_k)ei=(vj,vk) 表示边 eie_iei的起始顶点是 vjv_jvj，终止顶点是 vkv_kvk，即 vj→eivkv_j\xrightarrow[]{~e_i~}v_kvj ei vk。我们定义关联矩阵 A=[aij]为一m×nA=[a_{ij}] 为一 m\times nA=[aij]为一m×n 阶矩阵，其中 aij=−1a_{ij}=-1aij=−1 且 aik=+1a_{ik}=+1aik=+1 若 ei=(vj,vk)e_i=(v_j,v_k)ei=(vj,vk)，其余元为零。

举例：家庭成员5人，即∣V∣=5|V|=5∣V∣=5

对应关联矩阵 > $\displaystyle A=\bordermatrix{ ~&v_1&v_2&v_3&v_4&v_5\cr e_1&-1&1&0&0&0\cr e_2&1&0&-1&0&0\cr e_3&-1&0&0&1&0\cr e_4&0&-1&0&0&1\cr e_5&0&0&1&0&-1\cr e_6&0&0&0&1&-1 }$

注：关联矩阵的应用其中有基尔霍夫定理

2.1.2 一些图论相关基础知识

A 特征空间：

若{λ1,...,λi,...,λr}\{ \lambda_1,...,\lambda_i,...,\lambda_r\}{λ1,...,λi,...,λr}代表互不相同的特征值，那么特征空间SiS_iSi是由上述特征向量撑起：Si={x∈Rn∣Ax=λix}S_i=\{x\in \R^n | \rm A x=\lambda_i x\}Si={x∈Rn∣Ax=λix}如果λi!=λj\lambda_i !=\lambda_jλi!=λj则SiS_iSi与SjS_jSj正交。

B 图上的实值函数

考虑一个图上节点集合定义的实值函数f:V→R\rm f: V\rightarrow\Rf:V→R，这个方程fff分配具体的实值给图上每个节点

fff是由图上节点索引的向量，所以f∈Rn\rm f\in \R^nf∈Rn
我们记f\rm{f}f =(f(v1),...f(vn))=(f(1),...f(n))=(f(v_1),...f(v_n))=(f(1),...f(n))=(f(v1),...f(vn))=(f(1),...f(n))

其中上面的特征向量是邻接矩阵的特征向量。

C 邻接矩阵A作为算子和二次型形式时

注意这里用A表示邻接矩阵而不是W，因为这也是描述的比较混混的…

A作为算子时g=Af\rm g=Afg=Af g(i)=∑i→jf(j)g(i)=\sum_{i \rightarrow j }f(j)g(i)=i→j∑f(j)
使用A的二次型描述A的邻点权值：fTAf=∑eijf(i)f(j)\rm f^TAf = \sum_{e_ij}f(i)f(j)fTAf=eij∑f(i)f(j)其中eij是e_{ij}是eij是边集合中的第i到第j元素，没有忘吧。
至于算子是什么，个人理解是为了引出拉普拉斯矩阵的三种定义（算子，二次型和Random walk normalized Laplacian）

D 图的关联矩阵：

2.1.3 拉普拉斯矩阵

首先考虑图的关联矩阵（incidence matrix），C=C(G)C=C(G)C=C(G)。其中每一列表示的是图的节点，每一行表示的图的一条边。

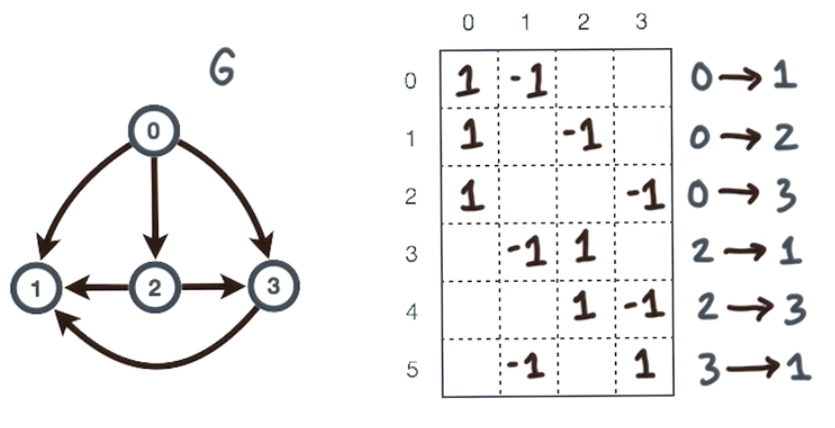
然后我们将这个关联矩阵可以写成：C=[e0Te1T⋮em−1T]C=\begin{bmatrix}e_0^T\\ e_1^T\\ \vdots\\ e_{m-1}^T\end{bmatrix}C=⎣⎢⎢⎢⎡e0Te1T⋮em−1T⎦⎥⎥⎥⎤其中，eke_kek是一个边向量，表达了从节点i到节点j的一条边:[⋯,1⏟i,⋯,−1⏟j,⋯][\cdots, \underbrace{1}_i, \cdots, \underbrace{-1}_j, \cdots][⋯,i1,⋯,j−1,⋯]这条边是从i到j，而且是直接通过，中间没有穿过任何节点（看上图），当我们描述“从节点i到节点j”时，就说其余位置都为0。所以：CTC=∑k=0m−1ek⋅ekTC^TC=\sum_{k=0}^{m-1}e_k \cdot e_k^TCTC=k=0∑m−1ek⋅ekT即：

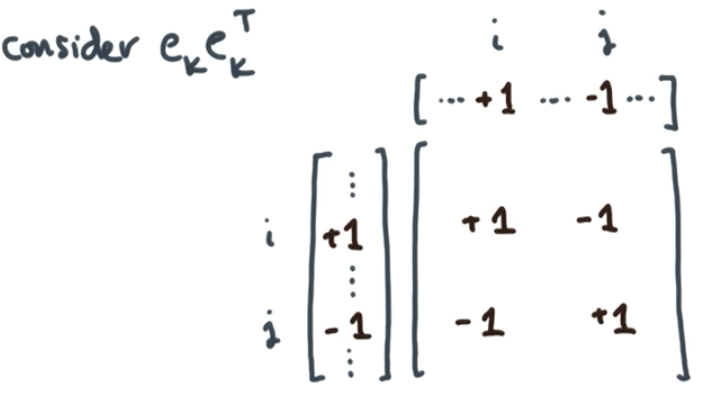
考虑上方这个矩阵，我们会发现它的对角线上，iiiiii这个位置和jjjjjj这个位置，会都为1，其实表达了在该图中，节点iii和jjj位置的度数为1。而其余两个位置ijijij和jijiji则表达了该位置存在一条边。此时，该矩阵损失了方向信息。

所以对上面一系列ekekTe_ke^T_kekekT矩阵求和，我们就得到了图的拉普拉斯矩阵，对角线表达了节点的度数，而非对角线部分则是边的信息。
那么，拉普拉斯矩阵就可以定义成：L=D−W(有些写成D−A)L=D-W(有些写成D-A)L=D−W(有些写成D−A)

当然，在有权图中，上面的关联矩阵，就不应该表示成1和-1，而应该是边的权重的平方根，那么对于平方根的处理，就需要用到刚刚的二次型思想。但这一过程并不是一蹴而就的，我们需要先更多地去描述一个有向图：

既然是有向图，就要用关联矩阵而不是邻接矩阵来描述LM。根据上面补充的知识，我们记f→∇f\rm f \rightarrow \nabla ff→∇f是图的共同边界映射(co-boundary)。（关联矩阵的转置代表着共同边界映射(coboundary map)）则(∇f)\rm (\nabla f)(∇f) (eij)=f(vj)−f(vi)(e_{ij})=f(v_j)-f(v_i)(eij)=f(vj)−f(vi)
反映在这个例子上：

就是：

19.12.17更新：这里说这个图的共同边界，是从教科书中拿下来的定义，但是通过在知乎上@superbrother写的关于拉普拉斯矩阵与拉普拉斯算子的关系的讨论中，我觉得可以从易接受的角度将其理解为就是在图空间中求其二阶微分（散度）。（ LLL是图的拉普拉斯矩阵）
也就是说，后文的(Lf)\rm (Lf)(Lf) (vi)(v_i)(vi) =(∇T∇)(vi)=(\nabla ^T\nabla)(v_i)=(∇T∇)(vi)=∑vj→vi(f(vi)−f(vj))\sum_{v_j\rightarrow v_i}(f(v_i)-f(v_j))∑vj→vi(f(vi)−f(vj))，可以将LfLfLf
看做在图空间中求L的二阶微分（这是后面进入LM后的内容）
上面这篇连接对深入理解GNN都是大有裨益的，自己有空了一定要多多品读大神的理解和看待问题的角度。

那么，既然要用权重的平方根，（又涉及到权重又涉及到平方根，你想到了什么？）
————我们用有权重的关联矩阵和描述平方根的二次型来描述有向图的拉普拉斯矩阵：L=∇T∇L=\nabla ^T\nablaL=∇T∇
∇T\nabla^T∇T是关联矩阵的转置，那么关联矩阵与他的转置之积是什么？

对于无向图，邻接矩阵与其转置之积对应两种情况：

AAT\rm AA^TAAT对角线上的表示顶点viv_ivi的出度

ATA\rm A^TAATA对角线上的表示顶点viv_ivi的入度

所以这里∇\nabla∇能表示顶点iii对其所有邻点jjj的关联矩阵
那么∇T\nabla^T∇T是不是反过来表示顶点jjj对其所有邻点iii的关联矩阵呢？

所以(Lf)\rm (Lf)(Lf) (vi)(v_i)(vi) =(∇T∇)(vi)=(\nabla ^T\nabla)(v_i)=(∇T∇)(vi)=∑vj→vi(f(vi)−f(vj))\sum_{v_j\rightarrow v_i}(f(v_i)-f(v_j))∑vj→vi(f(vi)−f(vj))

结合度矩阵和邻接矩阵，仍然可以：L=D−WL=D-WL=D−W但是这里的D是有向图的D

另外，对于有向图的LM我们有了，那么对于有权重的无向图(undirected weighted graph)，我们先考虑每条边eije_{ij}eij的权重wij>0w_{ij}>0wij>0
同样写出L作为operator和二次型的两种表示的形式

这个也很好理解，上面的无权值有向图的拉普拉斯矩阵中的节点viv_ivi值为所有向viv_ivi射过来的邻点vjv_jvj（所以求和符号下是右箭头，看到没，如果仅仅i射j就不计算他）的节点值求和，没有说权重就没有wijw_{ij}wij
而下面无向图有权重的，就求和符号两边都统计一波，然后顺便起一个wijw_{ij}wij，一下秒懂，有什么好说的。

3. 对Ncut的理解

既然我们用拉氏矩阵描述节点viv_ivi，那这么做一定是有助于谱聚类的。我们来看一下：
既然我们要谱图聚类，那就一定有一个目标函数，在文章《Normalized Cuts and Image Segmentation》中，作者给出了详细的推导过程，针对其中几个式子谈谈个人的浅显看法。

3.1 Computing the Optimal Partition

3.1.1 N-cut函数

这里关注−wijxixj-w_{ij}x_ix_j−wijxixj这项：

若i和j都在A割中，整体负号
若i和j都在B割中，整体负号
若i和j在不同的割图中，则整体正号

所以我们需要求出Ncut(A,B)Ncut(A,B)Ncut(A,B)的最小值，代表着割最少的边，经过最小的权重和，就能将两块蛋糕越完美的分开。
注意，公式中的xi,xjx_i,x_jxi,xj个人理解仅仅起到指示作用，就是说看这个点是上面三种情况中的哪一种，可以说是一种表示方式。

然后是文中的4Ncut(A,B):

我关注了式中的(D−W)(D-W)(D−W)，寻思着这不就是L吗？？我理解的这里的意思是，因为我们需要描述割图的目标函数，所以我们利用1+x2\frac{1+x}{2}21+x等变换构造出了quadratic form的Laplacian Matrix矩阵形式，从而利用了拉普拉斯矩阵的二次型函数作为normalized割图的目标函数。也就是说我理解的是作者根据这里构造出的D-W从而导出了拉普拉斯矩阵？

因为度矩阵（他后面分了A割图的度矩阵和B割图的度矩阵）就是i的邻点边数，在对角线上。而W是只有0或1组成的邻接矩阵（这里考虑最简单的情况进行思考），所以D-W就可以描述图中所有节点的相互连接性。因为之前不是说了吗，节点i和j位置的度数为1。而其余两个位置ij和ji则表达了该位置存在一条边。此时，该矩阵损失了方向信息。虽然方向没了但是我现在只需要知道i和j有一条边就行了，D-W正好可以反映无论是i到j还是j到i都有一条边，而且用(1+x)处理D-W阵中+1的元素，（1-x）处理-1的元素，求和就可以得到我一共鸽了多少条边！

理解GCN(二）从拉普拉斯矩阵到Ncut问题相关推荐

图谱论学习—拉普拉斯矩阵背后的含义
目录一.为什么学习拉普拉斯矩阵二.拉普拉斯矩阵的定义与性质三.拉普拉斯矩阵的推导与意义 3.1 梯度.散度与拉普拉斯算子 3.2 从拉普拉斯算子到拉普拉斯矩阵一.为什么学习拉普拉斯矩阵早期, ...
拉普拉斯矩阵（Laplace Matrix）与瑞利熵（Rayleigh quotient）
作者:桂. 时间:2017-04-13 07:43:03 链接:http://www.cnblogs.com/xingshansi/p/6702188.html 声明:欢迎被转载,不过记得注明出处哦 ...
非线性控制1.4——图论及拉普拉斯矩阵
一.图论相关概念图的概念:图用点代表各个事物,用边代表各个事物间的二元关系.所以,图是研究集合上的二元关系的工具,是建立数学模型的一个重要手段. 1.1 无向图概念实例: 给定无向图G＝<V ...
GCN频域视角相关——傅里叶变换、拉普拉斯变换、拉普拉斯算子、拉普拉斯矩阵、卷积
试图通俗地捋清标题名词之间的关系 0. 前置知识 0.1 函数的正交 0.2 什么是卷积? 0.3 散度 0.4 欧拉公式 1. 卷积与傅里叶变换 1.1 傅里叶变换 1.2 时域的卷积等于频域的乘积 ...
图卷积网络原理（二）【图信号与图的拉普拉斯矩阵】
矩阵乘法的三种视角后续图卷积网络的原理讲解主要以矩阵乘法的显示展开,这里介绍矩阵乘法的几种不同的视角,这些视角有助于我们理解图卷积网络的逻辑过程. 对于矩阵 A∈Rm×nA\in R^{m\time ...
【Pytorch神经网络理论篇】 25 基于谱域图神经网络GNN：基础知识+GNN功能+矩阵基础+图卷积神经网络+拉普拉斯矩阵
图神经网络(Graph Neural Network,GNN)是一类能够从图结构数据中学习特征规律的神经网络,是解决图结构数据(非欧氏空间数据)机器学习问题的最重要的技术. 1 图神经网络的基础知识 ...
从拉普拉斯矩阵说到谱聚类
从拉普拉斯矩阵说到谱聚类 0 引言 11月1日上午,机器学习班第7次课,邹博讲聚类(PPT),其中的谱聚类引起了自己的兴趣,他从最基本的概念:单位向量.两个向量的正交.方阵的特征值和特征向量,讲到相似 ...
拉普拉斯矩阵拉普拉斯算子图论
图函数我们知道,互相连接的节点可以构成一个图,其中包含所有节点构成的集合V,和所有边构成的集合E. 对于实数域上的函数y=f(x)y=f(x)y=f(x), 我们可以理解为一种对于x的映射,将每个可 ...
图拉普拉斯矩阵的定义、推导、性质、应用
导语:在学习图神经网络时,不可避免地要遇到拉普拉斯算子,拉普拉斯矩阵,图傅里叶变换,拉普拉斯特征分解向量等等一堆概念,了解其中的来源,定义,推导,对于后续图卷积神经网络的演进过程会有更深刻的理解文章 ...

理解GCN(二）从拉普拉斯矩阵到Ncut问题