An Implementation of Double-Array Trie

Contents

  1. What is Trie?
  2. What Does It Take to Implement a Trie?
  3. Tripple-Array Trie
  4. Double-Array Trie
  5. Suffix Compression
  6. Key Insertion
  7. Key Deletion
  8. Double-Array Pool Allocation
  9. An Implementation
  10. Download
  11. Other Implementations
  12. References

What is Trie?

Trie is a kind of digital search tree. (See [Knuth1972] for the detail of digital search tree.) [Fredkin1960] introduced the trie terminology, which is abbreviated from "Retrieval".

Trie is an efficient indexing method. It is indeed also a kind of deterministic finite automaton (DFA) (See [Cohen1990], for example, for the definition of DFA). Within the tree structure, each node corresponds to a DFA state, each (directed) labeled edge from a parent node to a child node corresponds to a DFA transition. The traversal starts at the root node. Then, from head to tail, one by one character in the key string is taken to determine the next state to go. The edge labeled with the same character is chosen to walk. Notice that each step of such walking consumes one character from the key and descends one step down the tree. If the key is exhausted and a leaf node is reached, then we arrive at the exit for that key. If we get stuck at some node, either because there is no branch labeled with the current character we have or because the key is exhausted at an internal node, then it simply implies that the key is not recognized by the trie.

Notice that the time needed to traverse from the root to the leaf is not dependent on the size of the database, but is proportional to the length of the key. Therefore, it is usually much faster than B-tree or any comparison-based indexing method in general cases. Its time complexity is comparable with hashing techniques.

In addition to the efficiency, trie also provides flexibility in searching for the closest path in case that the key is misspelled. For example, by skipping a certain character in the key while walking, we can fix the insertion kind of typo. By walking toward all the immediate children of one node without consuming a character from the key, we can fix the deletion typo, or even substitution typo if we just drop the key character that has no branch to go and descend to all the immediate children of the current node.

What Does It Take to Implement a Trie?

In general, a DFA is represented with a transition table, in which the rows correspond to the states, and the columns correspond to the transition labels. The data kept in each cell is then the next state to go for a given state when the input is equal to the label.

This is an efficient method for the traversal, because every transition can be calculated by two-dimensional array indexing. However, in term of space usage, this is rather extravagant, because, in the case of trie, most nodes have only a few branches, leaving the majority of the table cells blanks.

Meanwhile, a more compact scheme is to use a linked list to store the transitions out of each state. But this results in slower access, due to the linear search.

Hence, table compression techniques which still allows fast access have been devised to solve the problem.

  1. [Johnson1975] (Also explained in [Aho+1985] pp. 144-146) represented DFA with four arrays, which can be simplified to three in case of trie. The transition table rows are allocated in overlapping manner, allowing the free cells to be used by other rows.
  2. [Aoe1989] proposed an improvement from the three-array structure by reducing the arrays to two.

Tripple-Array Trie

As explained in [Aho+1985] pp. 144-146, a DFA compression could be done using four linear arrays, namely default, base, next, and check. However, in a case simpler than the lexical analyzer, such as the mere trie for information retrieval, the default array could be omitted. Thus, a trie can be implemented using three arrays according to this scheme.

Structure

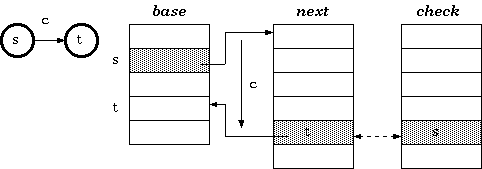
The tripple-array structure is composed of:

  1. base. Each element in base corresponds to a node of the trie. For a trie node s, base[s] is the starting index within the next and check pool (to be explained later) for the row of the node s in the transition table.
  2. next. This array, in coordination with check, provides a pool for the allocation of the sparse vectors for the rows in the trie transition table. The vector data, that is, the vector of transitions from every node, would be stored in this array.
  3. check. This array works in parallel to next. It marks the owner of every cell in next. This allows the cells next to one another to be allocated to different trie nodes. That means the sparse vectors of transitions from more than one node are allowed to be overlapped.

Definition 1. For a transition from state s to t which takes character c as the input, the condition maintained in the tripple-array trie is:

check[base[s] + c] = s
next[base[s] + c] = t

Walking

According to definition 1, the walking algorithm for a given state s and the input character c is:

t := base[s] + c;
if check[t] = s then next state := next[t] else fail endif

Construction

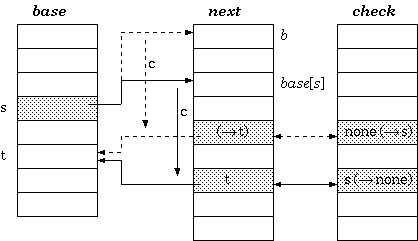
To insert a transition that takes character c to traverse from a state s to another state t, the cell next[base[s] + c]] must be managed to be available. If it is already vacant, we are lucky. Otherwise, either the entire transition vector for the current owner of the cell or that of the state sitself must be relocated. The estimated cost for each case could determine which one to move. After finding the free slots to place the vector, the transition vector must be recalculated as follows. Assuming the new place begins at b, the procedure for the relocation is:

Procedure Relocate(s : state; b : base_index){ Move base for state s to a new place beginning at b }begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } next[b + c] := next[base[s] + c]; { copy data } check[base[s] + c] := none { free the cell } end; base[s] := bend

Double-Array Trie

The tripple-array structure for implementing trie appears to be well defined, but is still not practical to keep in a single file. The next/check pool may be able to keep in a single array of integer couples, but the base array does not grow in parallel to the pool, and is therefore usually split.

To solve this problem, [Aoe1989] reduced the structure into two parallel arrays. In the double-array structure, the base and next are merged, resulting in only two parallel arrays, namely, base and check.

Structure

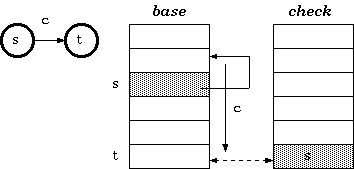
Instead of indirectly referencing through state numbers as in tripple-array trie, nodes in double-array trie are linked directly within the base/checkpool.

Definition 2. For a transition from state s to t which takes character c as the input, the condition maintained in the double-array trie is:

check[base[s] + c] = s
base[s] + c = t

Walking

According to definition 2, the walking algorithm for a given state s and the input character c is:

t := base[s] + c;
if check[t] = s then next state := t else fail endif

Construction

The construction of double-array trie is in principle the same as that of tripple-array trie. The difference is the base relocation:

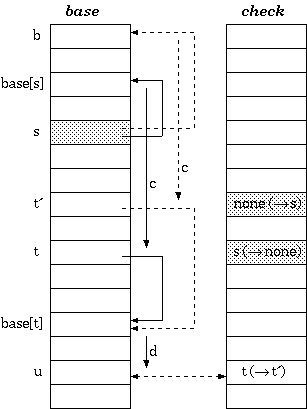
Procedure Relocate(s : state; b : base_index){ Move base for state s to a new place beginning at b }begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } base[b + c] := base[base[s] + c]; { copy data } { the node base[s] + c is to be moved to b + c; Hence, for any i for which check[i] = base[s] + c, update check[i] to b + c } foreach input character d for the node base[s] + c begin check[base[base[s] + c] + d] := b + c end; check[base[s] + c] := none { free the cell } end; base[s] := bend

Suffix Compression

[Aoe1989] also suggested a storage compression strategy, by splitting non-branching suffixes into single string storages, called tail, so that the rest non-branching steps are reduced into mere string comparison.

With the two separate data structures, double-array branches and suffix-spool tail, key insertion and deletion algorithms must be modified accordingly.

Key Insertion

To insert a new key, the branching position can be found by traversing the trie with the key one by one character until it gets stuck. The state where there is no branch to go is the very place to insert a new edge, labeled by the failing character. However, with the branch-tail structure, the insertion point can be either in the branch or in the tail.

1. When the branching point is in the double-array structure

Suppose that the new key is a string a1a2...ah-1ahah+1...an, where a1a2...ah-1 traverses the trie from the root to a node sr in the double-array structure, and there is no edge labeled ah that goes out of sr. The algorithm called A_INSERT in [Aoe1989] does as follows:

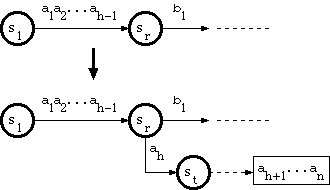
From sr, insert edge labeled ah to new node st;Let st be a separate node poining to a string ah+1...an in tail pool.

2. When the branching point is in the tail pool

Since the path through a tail string has no branch, and therefore corresponds to exactly one key, suppose that the key corresponding to the tail is

a1a2...ah-1ah...ah+k-1b1...bm,

where a1a2...ah-1 is in double-array structure, and ah...ah+k-1b1...bm is in tail. Suppose that the substring a1a2...ah-1 traverses the trie from the root to a node sr.

And suppose that the new key is in the form

a1a2...ah-1ah...ah+k-1ah+k...an,

where ah+k <> b1. The algorithm called B_INSERT in [Aoe1989] does as follows:

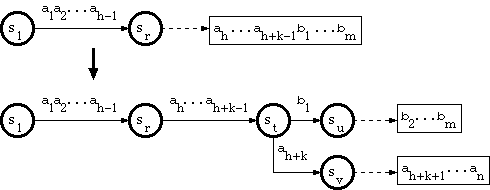
From sr, insert straight path with ah...ah+k-1, ending at a new node st;From st, insert edge labeled b1 to new node su;Let su be separate node pointing to a string b2...bm in tail pool;From st, insert edge labeled ah+k to new node sv;Let sv be separate node pointing to a string ah+k+1...an in tail pool.

Key Deletion

To delete a key from the trie, all we need to do is delete the tail block occupied by the key, and all double-array nodes belonging exclusively to the key, without touching any node belonging to other keys.

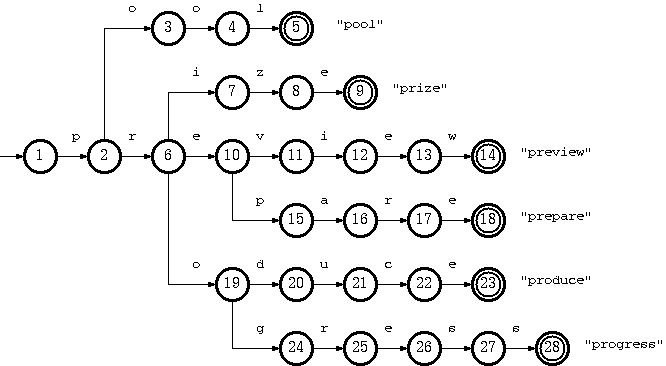
Consider a trie which accepts a language K = {pool#, prepare#, preview#, prize#, produce#, producer#, progress#} :

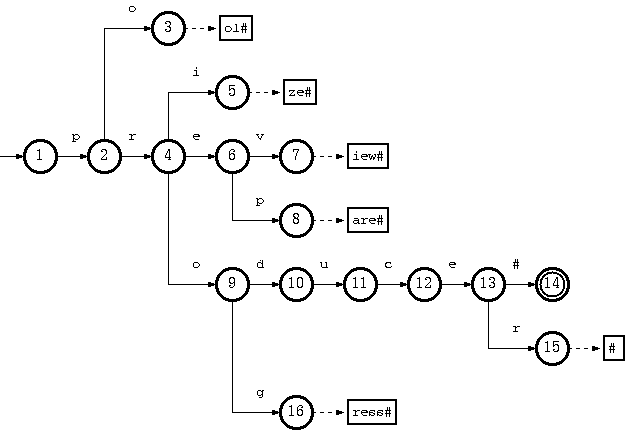
The key "pool#" can be deleted by removing the tail string "ol#" from the tail pool, and node 3 from the double-array structure. This is the simplest case.

To remove the key "produce#", it is sufficient to delete node 14 from the double-array structure. But the resulting trie will not obay the convention that every node in the double-array structure, except the separate nodes which point to tail blocks, must belong to more than one key. The path from node 10 on will belong solely to the key "producer#".

But there is no harm violating this rule. The only drawback is the uncompactnesss of the trie. Traversal, insertion and deletion algoritms are intact. Therefore, this should be relaxed, for the sake of simplicity and efficiency of the deletion algorithm. Otherwise, there must be extra steps to examine other keys in the same subtree ("producer#" for the deletion of "produce#") if any node needs to be moved from the double-array structure to tail pool.

Suppose further that having removed "produce#" as such (by removing only node 14), we also need to remove "producer#" from the trie. What we have to do is remove string "#" from tail, and remove nodes 15, 13, 12, 11, 10 (which now belong solely to the key "producer#") from the double-array structure.

We can thus summarize the algorithm to delete a key k = a1a2...ah-1ah...an, where a1a2...ah-1 is in double-array structure, and ah...an is in tail pool, as follows :

Let sr := the node reached by a1a2...ah-1;Delete ah...an from tail;s := sr;repeat p := parent of s; Delete node s from double-array structure; s := puntil s = root or outdegree(s) > 0.

Where outdegree(s) is the number of children nodes of s.

Double-Array Pool Allocation

When inserting a new branch for a node, it is possible that the array element for the new branch has already been allocated to another node. In that case, relocation is needed. The efficiency-critical part then turns out to be the search for a new place. A brute force algoritm iterates along the checkarray to find an empty cell to place the first branch, and then assure that there are empty cells for all other branches as well. The time used is therefore proportional to the size of the double-array pool and the size of the alphabet.

Suppose that there are n nodes in the trie, and the alphabet is of size m. The size of the double-array structure would be n + cm, where c is a coefficient which is dependent on the characteristic of the trie. And the time complexity of the brute force algorithm would be O(nm + cm2).

[Aoe1989] proposed a free-space list in the double-array structure to make the time complexity independent of the size of the trie, but dependent on the number of the free cells only. The check array for the free cells are redefined to keep a pointer to the next free cell (called G-link) :

Definition 3. Let r1, r2, ... , rcm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :

check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = -1

By this definition, negative check means unoccupied in the same sense as that for "none" check in the ordinary algorithm. This encoding scheme forms a singly-linked list of free cells. When searching for an empty cell, only cm free cells are visited, instead of all n + cm cells as in the brute force algorithm.

This, however, can still be improved. Notice that for those cells with negative check, the corresponding base's are not given any definition. Therefore, in our implementation, Aoe's G-link is modified to be doubly-linked list by letting base of every free cell points to a previous free cell. This can speed up the insertion and deletion processes. And, for convenience in referencing the list head and tail, we let the list be circular. The zeroth node is dedicated to be the entry point of the list. And the root node of the trie will begin with cell number one.

Definition 4. Let r1, r2, ... , rcm be the free cells in the double-array structure, ordered by position. G-link is defined as follows :

check[0] = -r1
check[ri] = -ri+1 ; 1 <= i <= cm-1
check[rcm] = 0
base[0] = -rcm
base[r1] = 0
base[ri+1] = -ri ; 1 <= i <= cm-1

Then, the searching for the slots for a node with input symbol set P = {c1, c2, ..., cp} needs to iterate only the cells with negative check :

{find least free cell s such that s > c1}s := -check[0];while s <> 0 and s <= c1 do s := -check[s]end;if s = 0 then return FAIL; {or reserve some additional space}{continue searching for the row, given that s matches c1}while s <> 0 do i := 2; while i <= p and check[s + ci - c1] < 0 do i := i + 1 end; if i = p + 1 then return s - c1; {all cells required are free, so return it} s := -check[s]end;return FAIL; {or reserve some additional space}

The time complexity for free slot searching is reduced to O(cm2). The relocation stage takes O(m2). The total time complexity is therefore O(cm2 + m2) = O(cm2).

It is useful to keep the free list ordered by position, so that the access through the array becomes more sequential. This would be beneficial when the trie is stored in a disk file or virtual memory, because the disk caching or page swapping would be used more efficiently. So, the free cell reusing should maintain this strategy :

t := -check[0];while check[t] <> 0 and t < s do t := -check[t]end;{t now points to the cell after s' place}check[s] := -t;check[-base[t]] := -s;base[s] := base[t];base[t] := -s;

Time complexity of freeing a cell is thus O(cm).

An Implementation

In my implementation, I designed the API with persistent data in mind. Tries can be saved to disk and loaded for use afterward. And in newer versions, non-persistent usage is also possible. You can create a trie in memory, populate data to it, use it, and free it, without any disk I/O. Alternatively you can load a trie from disk and save it to disk whenever you want.

The trie data is portable across platforms. The byte order in the disk is always little-endian, and is read correctly on either little-endian or big-endian systems.

Trie index is 32-bit signed integer. This allows 2,147,483,646 (231 - 2) total nodes in the trie data, which should be sufficient for most problem domains. And each data entry can store a 32-bit integer value associated to it. This value can be used for any purpose, up to your needs. If you don't need to use it, just store some dummy value.

For sparse data compactness, the trie alphabet set should be continuous, but that is usually not the case in general character sets. Therefore, a map between the input character and the low-level alphabet set for the trie is created in the middle. You will have to define your input character set by listing their continuous ranges of character codes in a .abm (alphabet map) file when creating a trie. Then, each character will be automatically assigned internal codes of continuous values.

Download

Update: The double-array trie implementation has been simplified and rewritten from scratch in C, and is now named libdatrie. It is now available under the terms of GNU Lesser General Public License (LGPL):

  • libdatrie-0.2.4 (30 June 2010)
  • libdatrie-0.2.3 (27 February 2010)
  • libdatrie-0.2.2 (29 April 2009)
  • libdatrie-0.2.1 (5 April 2009)
  • libdatrie-0.2.0 (24 March 2009)
  • libdatrie-0.1.3 (28 January 2008)
  • libdatrie-0.1.2 (25 August 2007)
  • libdatrie-0.1.1 (12 October 2006)
  • libdatrie-0.1.0 (18 September 2006)

SVN: svn co http://linux.thai.net/svn/software/datrie

The old C++ source code below is under the terms of GNU Lesser General Public License (LGPL):

  • midatrie-0.3.3 (2 October 2001)
  • midatrie-0.3.3 (16 July 2001)
  • midatrie-0.3.2 (21 May 2001)
  • midatrie-0.3.1 (8 May 2001)
  • midatrie-0.3.0 (23 Mar 2001)

Other Implementations

  • DoubleArrayTrie: Java implementation by Christos Gioran (More information)

References

  1. [Knuth1972] Knuth, D. E. The Art of Computer Programming Vol. 3, Sorting and Searching. Addison-Wesley. 1972.
  2. [Fredkin1960] Fredkin, E. Trie Memory. Communication of the ACM. Vol. 3:9 (Sep 1960). pp. 490-499.
  3. [Cohen1990] Cohen, D. Introduction to Theory of Computing. John Wiley & Sons. 1990.
  4. [Johnson1975] Johnson, S. C. YACC-Yet another compiler-compiler. Bell Lab. NJ. Computing Science Technical Report 32. pp.1-34. 1975.
  5. [Aho+1985] Aho, A. V., Sethi, R., Ullman, J. D. Compilers : Principles, Techniques, and Tools. Addison-Wesley. 1985.
  6. [Aoe1989] Aoe, J. An Efficient Digital Search Algorithm by Using a Double-Array Structure. IEEE Transactions on Software Engineering. Vol. 15, 9 (Sep 1989). pp. 1066-1077.
  7. [Virach+1993] Virach Sornlertlamvanich, Apichit Pittayaratsophon, Kriangchai Chansaenwilai. Thai Dictionary Data Base Manipulation using Multi-indexed Double Array Trie. 5th Annual Conference. National Electronics and Computer Technology Center. Bangkok. 1993. pp 197-206. (in Thai)

Theppitak Karoonboonyanan
Created: 1999-06-13
Last Updated 2012-12-02
Back to Theppitak's Homepage

Copyright © 1999 by Theppitak Karoonboonyanan, Software and Language Engineering Laboratory, National Electronics and Computer Technology Center. All rights reserved.

Copyright © 2003-2010 by Theppitak Karoonboonyanan. All rights reserved.

Double-Array Trie快速入门

shiqi.cui<cuberub@gmail.com>
May 24, 2009

1. Trie

Trie是一种搜索树，因“Retrieval”而得名。在以Trie树组织的词典里，所有词条的公共前缀是压缩存储的，即只会存储一份，所以又称前缀树。如图所示：

Trie可以理解为确定有限状态自动机，即DFA。在Trie树中，每个节点表示一个状态，每条边表示一个字符，从根节点到叶子节点经过的边即表示一个词条。查找一个词条最多耗费的时间只受词条长度影响，因此Trie的查找性能是很高的，跟哈希算法的性能相当。

2. Trie存储方式

Trie可以按照树的方式存储。每个节点包含n个指针，分别指向n个后续节点，每条边对应着一个输入字符。这样，每个节点的指针个数是跟字符表的大小相关的。如果按照链表的方式组织n个指针，查询的效率会比较低；如果以定长数组表示n个指针，占用的空间会比较大，基本是不可接受的。

Trie也可以按照DFA的方式存储，即表示为转移矩阵。行表示状态，列表示输入字符，(行, 列)位置表示转移状态。这种方式的查询效率很高，但由于稀疏的现象严重，空间利用效率很低。也可以采用压缩的存储方式即链表来表示状态转移，但查询效率无法满足要求。

为了解决上面的问题，有学者依次设计出了Four-Array Trie，Triple-Array Trie和Double-Array Trie结构，其得名源于内部采用的数组的个数。

3. Double-Array Trie

Double-Array Trie包含base和check两个数组。base数组的每个元素表示一个Trie节点，即一个状态；check数组表示某个状态的前驱状态。

base和check的关系满足下述条件：

base[s] + c = t

check[t] = s

其中，s是当前状态的下标，t是转移状态的下标，c是输入字符的数值。如图所示：

4. 查询过程

根据上述公式，查找某个字符串就非常简单。

假设初始状态为t0，字符序列是(c1, c2, …, cn)。那么，输入c1后的状态为t1 = base[t0] + c1，以此类推。

如果到某个状态是不合法的，那么查询失败；如果转到状态tn = base[tn-1] + c，并且tn是结束状态，那么查询成功；如果tn不是结束状态，那么查询失败。

5. 构建过程

首先，初始化base和check数组，元素默认值是0。随机确定初始状态t0及其base值，如t0=0, base[t0]=1。

对于插入词条，计算输入每个字符后的base位置。

如果该位置为空，则表示该位置可以插入，然后转到下一个字符；

如果该位置已有值，表示该位已经被其他的状态占用，这样需要调整其前驱状态的base值，以保证状态不会冲突，这个过程称为relocate。

6. 参考文档

1. http://linux.thai.net/~thep/datrie/datrie.html

绿色通道： 好文要顶 关注我 收藏该文与我联系

Double_array trie相关推荐

  1. BZOJ3166 [Heoi2013]Alo 【可持久化trie树 + 二分 + ST表】

    题目 Welcome to ALO ( Arithmetic and Logistic Online).这是一个VR MMORPG , 如名字所见,到处充满了数学的谜题. 现在你拥有n颗宝石,每颗宝石 ...

  2. usaco Cowxor (trie 树）

    没想到trie树还可以用在这上面,厉害厉害. [分析]这是字母树的经典应用.首先因为是求xor的最大值,可以用前缀和计算xor值,然后n^2枚举即可. [cpp] view plaincopy for ...

  3. 字符串匹配算法 -- AC自动机 基于Trie树的高效的敏感词过滤算法

    文章目录 1. 算法背景 2. AC自动机实现原理 2.1 构建失败指针 2.2 依赖失败指针过滤敏感词 3. 复杂度及完整代码 1. 算法背景 之前介绍过单模式串匹配的高效算法:BM和KMP 以及 ...

  4. 字符串匹配数据结构 --Trie树 高效实现搜索词提示 / IDE自动补全

    文章目录 1. 算法背景 2. Trie 树实现原理 2.1 Trie 树的构建 2.2 Trie树的查找 2.3 Trie树的遍历 2.4 Trie树的时间/空间复杂度 2.5 Trie 树 Vs ...

  5. POJ 2418 Hardwood Species(trie 树）

    题目链接 开始想用map的,字典序不会搞,还是老老实实的用trie树把.好久没写了,忘得差不多了. 1 #include <iostream> 2 #include <cstdio& ...

  6. Kanade's trio 2017多校#3 trie

    求数组中i<j<k 并且ai^aj<aj^ak的三元组组数 枚举插入ak,让ak中每一位作为最高位,查找字典树内最高位不同的数字数量 注意把ak的每个前缀做一个bad标记 存储让这个 ...

  7. [您有新的未分配科技点]可，可，可持久化！？------0-1Trie和可持久化Trie普及版讲解...

    这一次,我们来了解普通Trie树的变种:0-1Trie以及在其基础上产生的可持久化Trie(其实,普通的Trie也可以可持久化,只是不太常见) 先简单介绍一下0-1Trie:一个0-1Trie节点只有 ...

  8. 【bzoj3261】最大异或和 可持久化Trie树

    题目描述 给定一个非负整数序列 {a},初始长度为 N.        有M个操作,有以下两种操作类型: 1.A x:添加操作,表示在序列末尾添加一个数 x,序列的长度 N+1. 2.Q l r x: ...

  9. 算法 | 动画+解析，轻松理解「Trie树」

    Trie这个名字取自"retrieval",检索,因为Trie可以只用一个前缀便可以在一部字典中找到想要的单词. 虽然发音与「Tree」一致,但为了将这种 字典树 与 普通二叉树 ...

最新文章

  1. 1、excel常用技能（数据分列、数据快速浏览、转置、选择性粘贴运算、绘制对角线、单元格内换行、插入注解文字或图片）
  2. TCP/IP 总结一
  3. CodeForces - 1109A Sasha and a Bit of Relax(思维+异或和，好题)
  4. 基于深度学习模型WideDeep的推荐
  5. MapXtreme开发（二）
  6. java并发编程笔记--Executor相关API整理
  7. jdialog 数据量大加载出现白板_王者荣耀：队友真的有人机？白板熟练进排位，资料面都是假的...
  8. python做图片-python做图
  9. python 埋点_scala spark 埋点统计_spark—1:WordCount（Python与Scala对照）
  10. 关于最近有人恶意诽谤Yeslab的回应！
  11. 命名实体识别实践 - CRF
  12. QTableWidget
  13. 爬虫练习：南阳理工学院ACM题目信息
  14. Java导出Word文档的实现
  15. FPGA基础知识13(二级D触发器应用于同步器，减少亚稳态)
  16. macOS Outlook 查看邮件的源码 HTML源码
  17. Spring Cloud Netflix中文文档翻译笔记
  18. 什么是PE，PE有什么意义？
  19. JavaScript引用类型之Date类型
  20. 【b503】篝火晚会

热门文章

  1. python kil 掉子进程
  2. 阿拉伯数字改为中文大小写
  3. Android与鸿蒙系统安全（三）
  4. 一些前端开发实用的函数—1（jquery）
  5. 杭电计算机考研（初试+复试）经验分享
  6. 震撼，愿所有中国人，都能听到这篇演讲！
  7. 最新WannaRen病毒来袭，无力查杀？其来路早已被切断
  8. King of Glory刷金币脚本
  9. 为什么蚂蚁金服的 ZSearch 比 ElasticSearh 还牛逼？
  10. 判断平年还是闰年，一个月有多少天，一年的第几天