\(\\\)

\(Day\ 1\)

\(\\\)

\(\#\ A\) \(Rps\)

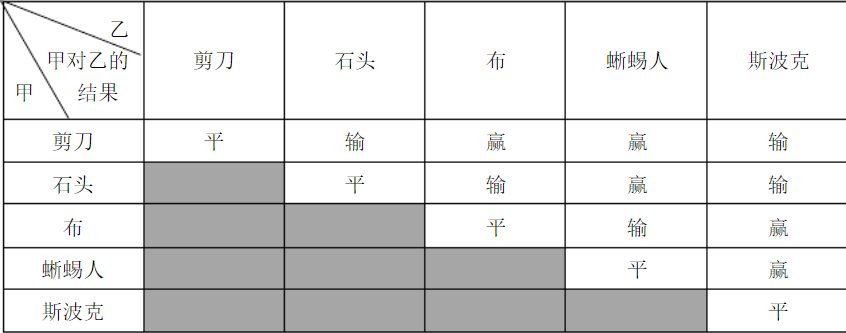
定义五种方案的石头剪刀布游戏，两人共进行\(N\)局游戏，已知两人各自的循环节和具体方案，胜者得\(1\)分，败者或平局均不得分，求\(N\)局后两人得分。

• \(N\in [0,200]\)

• 将二维的计分表填满，模拟。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 210
#define n1 x[0]
#define n2 y[0]
#define R register
#define gc getchar
using namespace std;int n,x[N],y[N];
int res[5][5]={{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1},{0,0,1,0,1},{1,1,0,0,0}
};inline int rd(){int x=0; bool f=0; char c=gc();while(!isdigit(c)){if(c=='-')f=1;c=gc();}while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}return f?-x:x;
}int main(){n=rd(); n1=rd(); n2=rd();for(R int i=1;i<=n1;++i) x[i]=rd();for(R int i=1;i<=n2;++i) y[i]=rd();int px=0,py=0,ansx=0,ansy=0;for(R int i=1;i<=n;++i){px=(px==n1)?1:px+1;py=(py==n2)?1:py+1;ansx+=res[x[px]][y[py]];ansy+=res[y[py]][x[px]];}printf("%d %d",ansx,ansy);return 0;
}

\(\\\)

\(\# B\) \(Link\)

给出一棵\(N\)个节点的树，每个边的边权都为\(1\)，每个点都有权值\(W_i\)，对于图\(G\)上的任意点对\((u,v)\)，若它们的最短距离为\(2\)，则它们之间会产生\(W_v \times W_u\)的联合权值，求：

• 整棵树所有点对中能够产生的最大联合权值
• 整棵树的所有能产生联合权值的点对间联合权值之和\((\)对\(10007\)取模\()\)
• \(N\in [0,2\times 10^5]\)，\(W_i\in [0,10^4]\)

• 每个能产生联合权值的点对必然会跨过一个中间点，也就是说，一个能产生联合权值的点对，必然存在一个另外的点，与这个点对中的两个点有边相连。
• 考虑枚举这个中间点，那么他直接连边的所有点任选两个都会产生联合权值，考虑用一种类似前缀和的方法，顺序扫描所有出边，每个点只与在它前面被扫描到的点\((\)仅本次枚举中间点所扫描到的点\()\)产生联合权值，这样计数可以保证复杂度对于每个点是线性的，并且不会重复计数。
• 对于最大值部分只需要在扫描过程中记录当前点所引出的点中最大权值点和次大权值点，每扫描一条出边就尝试更新最大值和次大值，最后得到的两个数相乘就是以当前点为中间点所能产生的最大联合权值。
• 注意点对是有序的，所以求和部分最后要取双倍答案。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 200010
#define R register
#define gc getchar
#define mod 10007
using namespace std;int n,tot,ansmx,ans,hd[N],val[N];
struct edge{int to,nxt;}e[N<<1];
inline void add(int u,int v){e[++tot].to=v; e[tot].nxt=hd[u]; hd[u]=tot;
}inline int rd(){int x=0; bool f=0; char c=gc();while(!isdigit(c)){if(c=='-')f=1;c=gc();}while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}return f?-x:x;
}inline void calc(int u){int sum=0,mx=0,sx=0;for(R int i=hd[u],v;i;i=e[i].nxt){v=e[i].to;if(val[v]>mx){sx=mx;mx=val[v];}else if(val[v]>sx) sx=val[v];(ans+=sum*val[v])%=mod;(sum+=val[v])%=mod;}ansmx=max(ansmx,mx*sx);
}int main(){n=rd();for(R int i=1,u,v;i<n;++i){u=rd(); v=rd(); add(u,v); add(v,u);}for(R int i=1;i<=n;++i) val[i]=rd();for(R int i=1;i<=n;++i) calc(i);printf("%d %d",ansmx,(ans<<1)%mod);return 0;
}

\(\\\)

\(\#C\) \(Bird\)

\(Flappy\ Bird\)，问题简化到了二维平面上，规定每次向上一次上升高度和每个位置不上升时的下降高度，具体问题描述见题目链接。

• \(N\in [1,10^4]\)，\(M\in [1,10^3]\)

• 设\(f[i][j]\)表示处理到第\(i\)列，到达高度为\(j\)的最少点击次数。
• 有显然的初始化\(f[i][j]=\infty\ \bigg|\ i\in[1,N],j\in[0,M]\)，注意到起点不能是地面，所以还有\(f[0][0]=\infty\)。

• 先不考虑水管高度和下降操作，对于每一个坐标\((i,j)\)，有显然的\(\text O(NM^2)\)的转移\(\begin{align} f[i][j]=min\{f[i-1][j-k\times up_i]+k\ \big| \ 1≤k≤\frac{j}{up_i}\}\end{align}\)

• 注意到转移方程都是统一的形式，\(f[i][j-up_i]\)已经帮助完成了除去\(f[i-1][j-up_i]\)以外的其他部分答案的统计，所以转移可以优化成\(\text O(NM)\)的形式：\(\begin{align}f[i][j]=min(f[i-1][j-up_i],f[i][j-up_i])+1\end{align}\)
• 注意到顶部的限制，\(f[i][M]\)的转移就多了很多，但是同样可以采用类似的方法优化：\(\begin{align}f[i][M]=min\{f[i][k]+1\ \big|\ k\in [M-up_i,M]\}\end{align}\)
• 然后再考虑下降部分，之所以这样按排顺序，是因为如果先更新下降部分的策略，可能会导致同一位置下降和上升同时出现，不合法。此部分的转移显然：\(\begin{align} f[i][j]=min(f[i][j],f[i-1][j+dn_i]\ \big|\ j+dn_i\le M) \end{align}\)

• 最后要考虑继续向后更新的合法性，将水管部分的答案全部重置为\(\infty\)。

• 答案可以倒着寻找，找到一个位置\(DP\)值不为\(\infty\)的即可作为答案，注意同时要更新经过的水管数。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 10010
#define M 1010
#define R register
#define gc getchar
#define inf 2000000000
using namespace std;int n,m,x,u[N],d[N],mx[N],mn[N],f[N][M];inline int rd(){int x=0; char c=gc();while(!isdigit(c)) c=gc();while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}return x;
}int main(){n=rd(); m=rd(); x=rd();for(R int i=1;i<=n;++i){u[i]=rd(); d[i]=rd(); mx[i]=m; mn[i]=1;}for(R int i=1,p;i<=x;++i){p=rd(); mn[p]=rd()+1; mx[p]=rd()-1;}for(R int i=1;i<=n;++i)for(R int j=0;j<=m;++j) f[i][j]=inf;for(R int i=1;i<=n;++i){for(R int j=1;j<=m;++j){if(j>=u[i]) f[i][j]=min(f[i][j],min(f[i-1][j-u[i]],f[i][j-u[i]])+1);if(j==m) for(R int k=j-u[i];k<=m;++k)f[i][j]=min(f[i][j],min(f[i-1][k],f[i][k])+1);}for(R int j=mn[i];j<=mx[i];++j)if(j+d[i]<=m) f[i][j]=min(f[i][j],f[i-1][j+d[i]]);for(R int j=0;j<mn[i];++j) f[i][j]=inf;for(R int j=mx[i]+1;j<=m;++j) f[i][j]=inf;}int ans=inf,cnt=x;for(R int i=n;i;--i){for(R int j=mn[i];j<=mx[i];++j) ans=min(ans,f[i][j]);if(ans<inf) break;if(mx[i]<m) --cnt;}(cnt==x)?printf("1\n%d\n",ans):printf("0\n%d\n",cnt);return 0;
}

\(\\\)

\(Day\ 2\)

\(\\\)

\(\#\ A\) \(Wireless\)

一个\(130\times 130\)的表格，一些格点有权，现在挑一个格点为中心选一个边长为\(2d\)的正方形，求这个正方形内\((\)含边界\()\)权值和最大值，以及可以产生此最大值的格点个数。

• \(d\in [1,20]\)，\(V_{ij}\in [0,10^6]\)

• 显然我们可以讲整个表格求二维前缀和，这样即可\(\Theta(1)\)地求出一个子正方形的权值。
• 把所有格点扫一遍即可，需要注意的是不能直接枚举子正方形顶点，因为会漏掉以边界为中心的一些子正方形，直接按照题目所说枚举中心点即可避免。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 150
#define R register
#define gc getchar
using namespace std;int n,d,res,cnt=1,sum[N][N];inline int rd(){int x=0; bool f=0; char c=gc();while(!isdigit(c)){if(c=='-')f=1;c=gc();}while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}return f?-x:x;
}int main(){d=rd(); n=rd();memset(sum,0,sizeof(sum));for(R int i=1,x,y;i<=n;++i){x=rd()+1; y=rd()+1; sum[x][y]+=rd();}for(R int i=1;i<N;++i)for(R int j=1;j<N;++j)sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];for(R int i=1;i<=129;++i)for(R int j=1;j<=129;++j){int x=i+d,y=j+d;int ans=sum[x][y]-sum[max(0,x-2*d-1)][y]-sum[x][max(0,y-2*d-1)]+sum[max(0,x-2*d-1)][max(0,y-2*d-1)];if(ans==res) ++cnt;if(ans>res) res=ans,cnt=1;}printf("%d %d\n",cnt,res);return 0;
}

\(\\\)

\(\#B\) \(Road\)

给出一张\(N\)个点\(M\)条边的有向图，且所有边权均为\(1\)，现规定起点\(U\)和终点\(V\)，找出一条从\(U\)到\(V\)的最短路径，且该路径需满足：路径上的所有点的出边所指向的点都直接或间接与终点连通。

求出符合条件的路径的长度，若不存在一条合法路径则输出"\(-1\)"。

• \(N\in [2,10^4]\)，\(M\in [1,2\times 10^5]\)

• 把问题转化为最短路，需要去掉所有满足“出边所指向的点中存在不与终点连通的点”的所有点，以及所有不与终点连通的点。
• 考虑正向求是否可达并不好处理，正难则反，把图建为原图的反图，从\(N\)开始做一遍\(BFS\)即可确定原图中每个点是否与终点连通，这样我们即可去除所有不与终点连通的点。

• 第一类不合法是由于联通了第二类不合法点导致的，所以在反图中我们同样可以找到原图里联通第二类不合法点的点，把他们也打上不合法标记，注意，这里的标记不能直接在原来存储第二类不合法点的数组中记录。

• 把不合法点都去除后，从\(N\)做一遍最短路即可。

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 10010
#define M 200010
#define R register
#define gc getchar
#define inf 10000000
using namespace std;bool vis[N],valid[N];
int n,m,tot,hd[N],dis[N],U,V;
struct edge{int to,nxt;}e[M];inline void add(int u,int v){e[++tot].to=v; e[tot].nxt=hd[u]; hd[u]=tot;
}inline int rd(){int x=0; bool f=0; char c=gc();while(!isdigit(c)){if(c=='-')f=1;c=gc();}while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=gc();}return f?-x:x;
}queue<int> q;
inline void bfs(){q.push(V); vis[V]=1;while(!q.empty()){int u=q.front(); q.pop();for(R int i=hd[u],v;i;i=e[i].nxt)if(!vis[v=e[i].to]){q.push(v); vis[v]=1;}}for(R int i=1;i<=n;++i) valid[i]=vis[i];for(R int i=1;i<=n;++i)if(!vis[i]) for(R int j=hd[i];j;j=e[j].nxt) valid[e[j].to]=0;
}priority_queue<pair<int ,int> >h;
inline void dij(){for(R int i=0;i<=n;++i) dis[i]=inf,vis[i]=0;dis[V]=0; h.push(make_pair(0,V));while(!h.empty()){int u=h.top().second; h.pop();if(vis[u]) continue; vis[u]=1;for(R int i=hd[u],v;i;i=e[i].nxt)if(valid[v=e[i].to]&&dis[v]>dis[u]+1){dis[v]=dis[u]+1; h.push(make_pair(-dis[v],v));}}
}int main(){n=rd(); m=rd();for(R int i=1,u,v;i<=m;++i){u=rd(); v=rd(); add(v,u);}U=rd(); V=rd(); bfs(); dij();printf("%d\n",dis[U]==inf?-1:dis[U]);return 0;
}

\(\\\)

\(\#C\) \(Equation\)

已知多项式方程：

\(\begin{align}a_0+a_1x+a_2x^2+\cdots+a_Nx^N=0\end{align}\)

求这个方程在\([1,M]\)内的整数解（\(N\)和\(M\)均为正整数）。

• \(N\in [1,100]\)，\(|a_i|\le 10^{10000}\)，\(M\in [0,10^6]\)

• 秦九韶公式减少方程计算次数，将\(x\)的每一层都嵌套起来，将方程变为如下形式：\(\begin{align}a_0+x(a_1+x(a_2+x(a_3+x(...+xa_n)...)))=0\end{align}\)此时，我们只需计算\(N\)次加法和\(N\)次乘法即可得到等式左边的答案。

• 枚举\([1,M]\)内的所有数，暴力带入验证即可，注意到系数给的非常大，即使是高精乘法也会超时，我们可以采用哈西的思想，将系数和计算所得都对同一个质数取模，验证最后的答案。这样的做法是不严谨的，所以我们考虑多用几个冲突较少的大质数去完成计算。

• 下面附的代码在洛谷上可通过，应该是当年\(Noip\)的数据，\(BZOJ\)上的数据加强了，这个版本的代码会超时到死都没有卡过40组数据10s的时限。

#include<cmath>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 110
#define M 1000010
#define R register
#define gc getchar
#define mod1 998244353ll
#define mod2 2147483647ll
#define mod3 3221225473ll
using namespace std;
typedef long long ll;ll n,m,res[M],a[3][N];inline void rd(ll p){bool f=0; char c=gc();while(!isdigit(c)){if(c=='-')f=1;c=gc();}while(isdigit(c)){a[0][p]=((a[0][p]<<1)+(a[0][p]<<3)+(c^48))%mod1;a[1][p]=((a[1][p]<<1)+(a[1][p]<<3)+(c^48))%mod2;a[2][p]=((a[2][p]<<1)+(a[2][p]<<3)+(c^48))%mod3;c=gc();}if(f){a[0][p]=-a[0][p]; a[1][p]=-a[1][p]; a[2][p]=-a[2][p];}
}inline bool valid(ll x){ll ans[3]={0ll,0ll,0ll};for(R int i=n;i;--i){ans[0]=(ans[0]+a[0][i])*x%mod1;ans[1]=(ans[1]+a[1][i])*x%mod2;ans[2]=(ans[2]+a[2][i])*x%mod3;}(ans[0]+=a[0][0])%=mod1;(ans[1]+=a[1][0])%=mod2;(ans[2]+=a[2][0])%=mod3;return (ans[0]==0&&ans[1]==0&&ans[2]==0);
}int main(){scanf("%lld%lld",&n,&m);for(R ll i=0;i<=n;++i) rd(i);for(R ll i=1;i<=m;++i) if(valid(i)) res[++res[0]]=i;printf("%lld\n",res[0]);for(R ll i=1;i<=res[0];++i) printf("%lld\n",res[i]);return 0;
}