[数论] 快速傅里叶变换FFT

模板链接：https://www.luogu.org/problemnew/show/P3803

【模板】多项式乘法（FFT）

题目背景

这是一道FFT模板题

注意：虽然本题开到3s，但是建议程序在1s内可以跑完，本题需要一定程度的常数优化。

题目描述

给定一个nnn次多项式F(x)" role="presentation" style="position: relative;">F(x)F(x)F(x)，和一个mmm次多项式G(x)" role="presentation" style="position: relative;">G(x)G(x)G(x)。

请求出F(x)F(x)F(x)和G(x)G(x)G(x)的卷积。

输入输出格式

输入格式：

第一行222个正整数n,m" role="presentation" style="position: relative;">n,mn,mn,m。

接下来一行n+1n+1n+1个数字，从低到高表示F(x)F(x)F(x)的系数。

接下来一行m+1m+1m+1个数字，从低到高表示G(x)G(x)G(x)的系数。

输出格式：

一行n+m+1n+m+1n+m+1个数字，从低到高表示F(x)∗G(x)F(x)∗G(x)F(x)∗G(x)的系数。

输入输出样例

输入样例#1：

1 2
1 2
1 2 1

输出样例#1：

1 4 5 2

说明

保证输入中的系数大于等于00 0 且小于等于999。

对于100%" role="presentation" style="position: relative;">100%100%100\%的数据：n,m≤106n,m≤106 n, m \leq {10}^6 , 共计20个数据点，2s。

数据有一定梯度。

空间限制：256MB

题解

FFTFFT\mathcal{FFT}学习，从入门到入土。。。

边写博客边加深一下理解吧。

1.复数

复数是实数和虚数的结合体，众所周知，实数可以表示在横向的数轴上，而虚数可以纵轴上，这样实数与虚数的两个坐标轴就构成了一个平面，一个复数的代数表示就是a+bia+bia+bi，aaa为实部，bi" role="presentation" style="position: relative;">bibibi为虚部，放在坐标轴中就是平面上的一个点了。

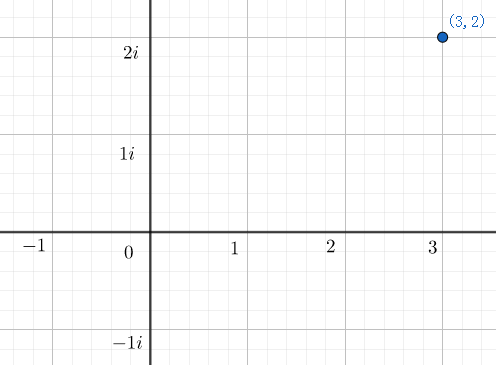
上图即为复数3+2i3+2i3+2i在复平面上的表示，显然，这样的表示是唯一对应的。

复数的运算法则：

加法：(a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)+(c+di)=(a+c)+(b+d)i

乘法：(a+bi)×(c+di)=(ac−bd)+(ad+bc)i(a+bi)×(c+di)=(ac−bd)+(ad+bc)i(a+bi)\times (c+di)=(ac-bd)+(ad+bc)i

对于加法，复数的运算与向量类似，但向量的运算法则不能很好的用在复数的乘法上，所以我们考虑用极坐标将一个复数表示为(r,θ)(r,θ)(r,\theta)，在这种表示下我们再来看复数乘法：

(r1cosθ1+r1sinθ1i)×(r2cosθ2+r2sinθ2i)=(r1r2cosθ1cosθ2−r1r2sinθ1sinθ2)+(r1r2cosθ1sinθ2+r1r2sinθ1cosθ2)i=(r1r2cos(θ1+θ2))+(r1r2sin(θ1+θ2))(r1cosθ1+r1sinθ1i)×(r2cosθ2+r2sinθ2i)=(r1r2cosθ1cosθ2−r1r2sinθ1sinθ2)+(r1r2cosθ1sinθ2+r1r2sinθ1cosθ2)i=(r1r2cos(θ1+θ2))+(r1r2sin(θ1+θ2))

(r_1cos\theta_1+r_1sin\theta_1i)\times(r_2cos\theta_2+r_2sin\theta_2i)\\ \begin{align*} &=(r_1r_2cos\theta_1cos\theta_2-r_1r_2sin\theta_1sin\theta_2)+(r_1r_2cos\theta_1sin\theta_2+r_1r_2sin\theta_1cos\theta_2)i\\ &=(r_1r_2cos(\theta_1+\theta_2))+(r_1r_2sin(\theta_1+\theta_2)) \end{align*}

新得到的复数的坐标就为(r1r2,θ1+θ2)(r1r2,θ1+θ2)(r_1r_2,\theta_1+\theta_2)，可以说是非常简洁而优美了。

2.单位根

单位根就是方程xn=1xn=1x^n=1在复数域的解。

单位根有什么特点呢？

假设一个单位根为(1,θ)(1,θ)(1,\theta)，它的nnn次方就是(1,n×θ)" role="presentation" style="position: relative;">(1,n×θ)(1,n×θ)(1,n\times\theta)，111在坐标轴上的坐标为(1,0)" role="presentation" style="position: relative;">(1,0)(1,0)(1,0)，那么就有n×θ=2kπ(k∈Z)n×θ=2kπ(k∈Z)n\times \theta=2k\pi(k\in Z)，解得θ=2kπn(k∈Z)θ=2kπn(k∈Z)\theta=\frac{2k\pi}{n}(k\in Z)，所以111的n" role="presentation" style="position: relative;">nnn次平方根共有nnn个，表示在复平面上就是n" role="presentation" style="position: relative;">nnn个将单位圆等分为nnn份的点，且其中一个为1" role="presentation" style="position: relative;">111。

我们将满足ωn=1ωn=1\omega^n=1的ωω\omega称为111的n" role="presentation" style="position: relative;">nnn次单位根，记做ωnωn\omega_n，并且用0∼n−10∼n−10\sim n-1标号，记做ω0n∼ωn−1nωn0∼ωnn−1\omega_n^0\sim \omega_n^{n-1}，下图为n=8n=8n=8时的单位根图像

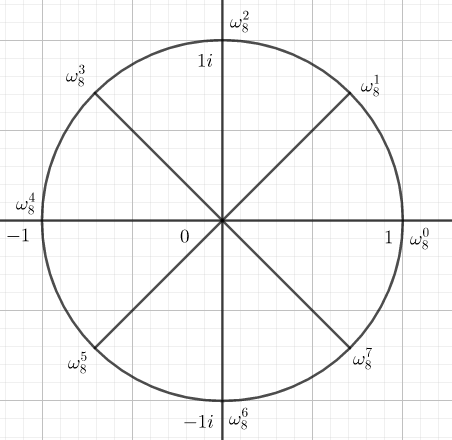
注意到ωkn=ωk+nn,ωkn=ωkxnxωnk=ωnk+n,ωnk=ωnxkx\omega_n^k=\omega_n^{k+n},\omega_n^k=\omega_{\frac{n}{x}}^{\frac{k}{x}}。

3.多项式的表示法

一个n−1n−1n-1次多项式的基本形式为：

f(x)=∑i=0naixif(x)=∑i=0naixi

f(x)=\sum_{i=0}^na_ix^i

我们称这种表示法为系数表示法，有了一个多项式的系数表达式，我们就能快速计算出代入的自变量xxx对应的函数值。

但是借助系数表示法无法快速求出两个多项式相乘后的多项式，考虑多项式相乘F(x)=f(x)×g(x)" role="presentation" style="position: relative;">F(x)=f(x)×g(x)F(x)=f(x)×g(x)F(x)=f(x)\times g(x)的本质事实上是对于自变量xxx的每个可能取值xi" role="presentation" style="position: relative;">xixix_i，都有F(xi)=f(xi)×g(xi)F(xi)=f(xi)×g(xi)F(x_i)=f(x_i)\times g(x_i)，这样看来，如果我们知道了两个多项式对于同一个横坐标xixix_i的点值，我们便能快速计算出它们相乘之后得到的多项式的点值。

由LagrangeLagrangeLagrange插值法可知，nnn个点可以唯一确定一个n−1" role="presentation" style="position: relative;">n−1n−1n-1阶多项式，那么我们就可以用这nnn个点来表示一个多项式，我们称这种表示法为点值表示法。

借助系数表示法，我们可以快速求出函数值；而通过点值表示法，我们可以快速完成多项式相乘的运算。

我们要计算两个多项式的乘积，就有了一个简单的思路：
(1)将两个多项式由系数表示转换为点值表示。
(2)将两个多项式的点值相乘，得到乘积多项式的点值。
(3)将新多项式由点值表示转换为系数表示。

4.快速傅里叶变换

在上述计算多项式相乘的思路中，复杂度瓶颈在于两种表示法之间的“转换”，朴素的实现是将自变量一一代入多项式求出对应的点值，复杂度为O(n2)" role="presentation" style="position: relative;">O(n2)O(n2)O(n^2)，并不优秀。

快速傅里叶变换（FFTFFT\mathcal{FFT}）便是突破瓶颈的关键，FFTFFT\mathcal{FFT}实现了两种快速表示法之间O(nlog2n)O(nlog2n)O(nlog_2n)的快速转换。

设nnn项多项式f(x)" role="presentation" style="position: relative;">f(x)f(x)f(x)，其中n=2k,α=2πn,ωn=cosα+sinαin=2k,α=2πn,ωn=cosα+sinαin=2^k,\alpha=\frac{2\pi}{n},\omega_n=cos\alpha+sin\alpha i，考虑用这nnn个单位根上的点值来表示多项式：

f(ωnk)=∑i=0n−1aiωnki" role="presentation" style="text-align: center; position: relative;">f(ωkn)=∑i=0n−1aiωkinf(ωnk)=∑i=0n−1aiωnki

f(\omega_n^k)=\sum_{i=0}^{n-1}a_i\omega_n^{ki}

我们可以分奇偶项将上面的式子拆成两个：

∑i=0n−1aiωkin=∑i=0n2−1a2iω2kin+∑i=0n2−1a2i+1ω(2i+1)kn=∑i=0n2−1a2iω2kin+ωkn(∑i=0n2−1a2i+1ω2kin)=∑i=0n2−1a2iωkin2+ωkn(∑i=0n2−1a2i+1ωkin2)∑i=0n−1aiωnki=∑i=0n2−1a2iωn2ki+∑i=0n2−1a2i+1ωn(2i+1)k=∑i=0n2−1a2iωn2ki+ωnk(∑i=0n2−1a2i+1ωn2ki)=∑i=0n2−1a2iωn2ki+ωnk(∑i=0n2−1a2i+1ωn2ki)

\begin{align*} \sum_{i=0}^{n-1}a_i\omega_n^{ki}&=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_n^{2ki}+\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_n^{(2i+1)k}\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_n^{2ki}+\omega_n^k(\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_n^{2ki})\\ &=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}\omega_{\frac{n}{2}}^{ki}+\omega_n^k(\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\omega_{\frac{n}{2}}^{ki}) \end{align*}

这样我们就得到了两个形式与f(x)f(x)f(x)相似的多项式，显然可以递归处理下去。同时，为了能够顺利分治到最底层，我们需要将多项式的项数补全到2k2k2^k。

让我们以888项的7" role="presentation" style="position: relative;">777次多项式为例，再仔细研究一下这个过程，设：

F(x)=a0+a1x+a2x2+⋯+a7x7f(x)=a0+a2x2+⋯+a6x6g(x)=a1+a3x2+⋯+a7x6F(x)=a0+a1x+a2x2+⋯+a7x7f(x)=a0+a2x2+⋯+a6x6g(x)=a1+a3x2+⋯+a7x6

F(x)=a_0+a_1x+a_2x^2+\cdots+a_7x^7\\ f(x)=a_0+a_2x^2+\cdots+a_6x^6\\ g(x)=a_1+a_3x^2+\cdots+a_7x^6

不难得到：F(x)=f(x2)+x×g(x2)F(x)=f(x2)+x×g(x2)F(x)=f(x^2)+x\times g(x^2)

将ωkn(k<n2)ωnk(k<n2)\omega_n^k(k代入这个式子：

F(ωkn)=f(ω2kn)+ωkn×g(ω2kn)F(ωnk)=f(ωn2k)+ωnk×g(ωn2k)

F(\omega_n^k)=f(\omega_n^{2k})+\omega_n^{k}\times g(\omega_n^{2k})

再代入ωk+n2nωnk+n2\omega_n^{k+\frac{n}{2}}：

F(ωk+n2n)=f(ω2k+nn)+ωk+n2n×g(ω2k+nn)=f(ω2kn)−ωkn×g(ω2kn)F(ωnk+n2)=f(ωn2k+n)+ωnk+n2×g(ωn2k+n)=f(ωn2k)−ωnk×g(ωn2k)

\begin{align*} F(\omega_n^{k+\frac{n}{2}})&=f(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}\times g(\omega_n^{2k+n})\\ &=f(\omega_n^{2k})-\omega_n^{k}\times g(\omega_n^{2k}) \end{align*}

震惊！F(ωk+n2n)F(ωnk+n2)F(\omega_n^{k+\frac{n}{2}})与F(ωkn)F(ωnk)F(\omega_n^k)只有一字之差！我们在枚举ωkn(k<n2)ωnk(k<n2)\omega_n^k(k的时候就可以O(1)O(1)O(1)得到ωk+n2nωnk+n2\omega_n^{k+\frac{n}{2}}的值。

在此基础上，我们又将问题缩小了一半，至此我便可以通过与线段树类似分治思想在O(nlog2n)O(nlog2n)O(nlog_2n)的时间复杂度内将一个多项式从系数表达式转换为点值表达式。

不仅如此，系数的位置变化也有不可告人的秘密：

(a0,a1,a2,a3,a4,a5,a6,a7)↓(a0,a2,a4,a6),(a1,a3,a5,a7)↓(a0,a4),(a2,a6),(a1,a5),(a3,a7)↓(a0),(a4),(a2),(a6),(a1),(a5),(a3),(a7)(a0,a1,a2,a3,a4,a5,a6,a7)↓(a0,a2,a4,a6),(a1,a3,a5,a7)↓(a0,a4),(a2,a6),(a1,a5),(a3,a7)↓(a0),(a4),(a2),(a6),(a1),(a5),(a3),(a7)

(a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7)\\ \downarrow \\ (a_0,a_2,a_4,a_6),(a_1,a_3,a_5,a_7)\\ \downarrow \\ (a_0,a_4),(a_2,a_6),(a_1,a_5),(a_3,a_7)\\ \downarrow \\ (a_0),(a_4),(a_2),(a_6),(a_1),(a_5),(a_3),(a_7)\\

似乎没有什么规律？让我们将收尾的二进制拿出来比较：

000,001,010,011,100,101,110,111000,100,010,110,001,101,011,111000,001,010,011,100,101,110,111000,100,010,110,001,101,011,111

000,001,010,011,100,101,110,111\\ 000,100,010,110,001,101,011,111
规律的气息：我们发现最后的序列的二进制等于初始序列二进制的翻转！

这个规律的本质便是我们每次都将系数按照奇偶分开，我们先将最后一位为000的放在前面，再将倒数第二位为0" role="presentation" style="position: relative;">000的数放在前面。。。以此类推，最后数列的比较方式实际上是从低位到高位比较，与初始序列相反，最后就得到了这样一个优美的性质。

这样，我们可以预先知道哪个位置上是哪个数，从底层开始向上合并，通过访问连续的内存使算法大大加快！

考虑如何处理出翻转后的数，我们可以借用前面的数处理出的信息，对于一个在二进制数有LLL位的数x" role="presentation" style="position: relative;">xxx，它的前L−1L−1L-1位翻转后与x>>1x>>1x>>1相同，所以我们只需要保留xxx的最后一位，将其放到第一位，然后把x>>1" role="presentation" style="position: relative;">x>>1x>>1x>>1的翻转结果拿过来就好了：

for(mx=1;mx<=n+m;mx<<=1,++len);
for(int i=0;i<mx;++i)rev[i]=(rev[i>>1]>>1|((i&1)<<(len-1)));

5.快速傅里叶反变换

考虑将代入自变量计算点值的过程表示成矩阵乘法：

先贴一发矩阵乘法运算法则：

设矩阵AAA为m×p" role="presentation" style="position: relative;">m×pm×pm\times p的矩阵，BBB为p×n" role="presentation" style="position: relative;">p×np×np\times n的矩阵，A×B=CA×B=CA\times B=C，那么有：

Ci,j=∑k=1pAi,k×Bk,jCi,j=∑k=1pAi,k×Bk,j

C_{i,j}=\sum_{k=1}^pA_{i,k}\times B_{k,j}

于是，我们可以将上述过程表示为如下的矩阵乘法，设nnn阶矩阵W" role="presentation" style="position: relative;">WWW满足Wi,j=ωijnWi,j=ωnijW_{i,j}=\omega_n^{ij}，以及长度为nnn的向量A" role="presentation" style="position: relative;">AAA表示f(x)f(x)f(x)的各个系数aiaia_i，就有W×A={f(ωin)|i∈[0,n−1]}W×A={f(ωni)|i∈[0,n−1]}W\times A=\{f(\omega_n^i)|i\in[0,n-1]\}：

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢1111⋮11w1nw2nw3n⋮wn−1n1w2nw4nw6n⋮w2(n−1)n1w3nw6nw9n⋮w3(n−1)n⋯⋯⋯⋯⋱⋯1wn−1nw2(n−1)nw3(n−1)n⋮w(n−1)2n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢a0a1a2a3⋮an−1⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢f(ω0n)f(ω1n)f(ω2n)f(ω3n)⋮f(ωn−1n)⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥[1111⋯11wn1wn2wn3⋯wnn−11wn2wn4wn6⋯wn2(n−1)1wn3wn6wn9⋯wn3(n−1)⋮⋮⋮⋮⋱⋮1wnn−1wn2(n−1)wn3(n−1)⋯wn(n−1)2][a0a1a2a3⋮an−1]=[f(ωn0)f(ωn1)f(ωn2)f(ωn3)⋮f(ωnn−1)]

\left[\begin{matrix} 1 &1 &1 &1 &\cdots &1\\ 1 &w_n^1 &w_n^2 &w_n^3 &\cdots &w_n^{n-1}\\ 1 &w_n^2 &w_n^4 &w_n^6 &\cdots &w_n^{2(n-1)}\\ 1 &w_n^3 &w_n^6 &w_n^9 &\cdots &w_n^{3(n-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots&\vdots \\ 1 &w_n^{n-1}&w_n^{2(n-1)} &w_n^{3(n-1)} &\cdots &w_n^{(n-1)^2}\\ \end{matrix}\right] \left[\begin{matrix} a_0 \\a_1 \\a_2\\a_3\\ \vdots\\a_{n-1}\\ \end{matrix}\right] {=} \left[\begin{matrix} f(\omega_n^0)\\f(\omega_n^1)\\f(\omega_n^2)\\f(\omega_n^3)\\ \vdots\\f(\omega_n^{n-1})\\ \end{matrix}\right]

那我们实际上要做的就是构造一个WWW的“倒数”即逆矩阵来抵消W" role="presentation" style="position: relative;">WWW，考虑nnn阶矩阵W′" role="presentation" style="position: relative;">W′W′W'，满足W′i,j=ω−ijnWi,j′=ωn−ijW'_{i,j}=\omega_n^{-ij}，就有WW′=n×InWW′=n×InWW'=n\times I_n，其中InInI_n为nnn阶单位矩阵，那么W" role="presentation" style="position: relative;">WWW的逆矩阵实际上就是1nW′1nW′\frac{1}{n}W'，所以我们只需要在正向变换上稍作改动，最后算出来的系数再除以项数就能完成从点值表示到系数表示的转换。

代码

其实STLSTLSTL有自带的复数类(complex)(complex)(complex)，运行效率你们懂得。。。

#include<bits/stdc++.h>
#define db double
using namespace std;
const int M=4e6+5;
const db pi=acos(-1.0);
struct cpx{db x,y;}f[M],g[M];
cpx operator +(cpx a,cpx b){return (cpx){a.x+b.x,a.y+b.y};}
cpx operator -(cpx a,cpx b){return (cpx){a.x-b.x,a.y-b.y};}
cpx operator *(cpx a,cpx b){return (cpx){a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
int n,m,mx,len,rev[M];
void in(){scanf("%d%d",&n,&m);for(int i=0;i<=n;++i)scanf("%lf",&f[i].x);for(int i=0;i<=m;++i)scanf("%lf",&g[i].x);}
void fft(cpx *f,int typ)
{cpx wn,w,x,y;int i,mid,j,k;for(i=0;i<mx;++i)if(i<rev[i])swap(f[i],f[rev[i]]);for(mid=1;mid<mx;mid<<=1)for(j=0,wn=(cpx){cos(pi/mid),typ*sin(pi/mid)};j<mx;j+=mid<<1)for(k=0,w=(cpx){1,0};k<mid;++k,w=w*wn)x=f[j+k],y=w*f[j+mid+k],f[j+k]=x+y,f[j+mid+k]=x-y;
}
void ac()
{for(mx=1;mx<=n+m;mx<<=1,++len);for(int i=0;i<mx;++i)rev[i]=(rev[i>>1]>>1|((i&1)<<(len-1)));fft(f,1);fft(g,1);for(int i=0;i<=mx;++i)f[i]=f[i]*g[i];fft(f,-1);for(int i=0;i<=n+m;++i)printf("%d ",int(f[i].x/mx+0.5));
}
int main(){in();ac();}