数学建模期末复习，撰写博客做总结之用，主要侧重于算例的模型建立与部分代码的实现，其中不足之处望读者多多指正。

Matlab微分求解工具箱使用

求数值解

dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’)

求解析解

[t，x]=solver(’f’,ts,x0,options)

详细的使用说明可参考博文Matlab微分方程求解

导弹问题

问题介绍

设位于坐标原点的甲舰向位于x轴上点A(1, 0)处的乙舰发射导弹，导弹头始终对准乙舰．如果乙舰以最大的速度v0v_0v0​(常数)沿平行于y轴的直线行驶，导弹的速度是5v0v_0v0​，求导弹运行的曲线方程．乙舰行驶多远时，导弹将它击中？

模型建立与求解

1. 解析法

模型建立：设t时刻导弹的位置为P(x(t),y(t)),乙舰位于Q(1,V0tV_0tV0​t)，由题(导弹头始终对准乙舰)可得，导弹在运动弧线p点处的切线y′=v0t−y1−xy^{\prime}=\frac{v_{0} t-y}{1-x}y′=1−xv0​t−y​即 v0t=(1−x)y′+y(1)v_{0} t=(1-x) y^{\prime}+y(1)v0​t=(1−x)y′+y(1)

又由题意(导弹速度是舰的5倍)故有：∫0x1+y′2dx=5v0t(2)\int_0^x {\sqrt {1 + y{'^2}} } {\rm{d}}x = 5{v_0}t (2)∫0x​1+y′2​dx=5v0​t(2)

有(1)(2)式可得微分微分方程为：(1−x)y′′=151+y′2(3)(1-x) y^{\prime \prime}=\frac{1}{5} \sqrt{1+y^{\prime 2}}(3)(1−x)y′′=51​1+y′2​(3)

初值方程为：y(0)=0y(0) = 0y(0)=0，y′(0)=0y'(0) = 0y′(0)=0，利用Matlab求解可得：y=−58(1−x)45+512(1−x)65+524y = - \frac{5}{8}{(1 - x)^{\frac{4}{5}}} + \frac{5}{{12}}{(1 - x)^{\frac{6}{5}}} + \frac{5}{{24}}y=−85​(1−x)54​+125​(1−x)56​+245​

2. 数值解法

将上述方程化为一阶方程，不妨设y1=y,y2=y′y_1=y,y_2=y'y1​=y,y2​=y′,代入(3)中得到{y1′=y2y2′=151+y12/(1−x)\left\{\begin{array}{l}y_{1}^{\prime}=y_{2} \\ y_{2}^{\prime}=\frac{1}{5} \sqrt{1+y_{1}^{2}} /(1-x)\end{array}\right.{y1′​=y2​y2′​=51​1+y12​​/(1−x)​

利用Matlab求解：

%定义函数

function dy=eq1(x,y)

dy=zeros(2,1);

dy(1)=y(2);

dy(2)=1/5*sqrt(1+y(1)^2)/(1-x);

end

调用

x0=0;

xf=0.9999;

[x,y]=ode15s('eq1',[x0 xf],[0 0]);

plot(x,y(:,1),'-')

hold on

y=0:0．01:2;

plot(1,y,'*')

复制代码

由图可得，导弹大致在点(1,0.2)处击中乙舰。

3. 参数方程

上述结题假设不变，在此基础再将导弹的速度设为www,则在P点处有：(dxdt)2+(dydt)2=w2(1){({{{\rm{d}}x} \over {{\rm{d}}t}})^2} + {({{{\rm{d}}y} \over {{\rm{d}}t}})^2} = {w^2}(1)(dtdx​)2+(dtdy​)2=w2(1)

同时，导弹始终对准乙舰，即导弹速度向量与乙舰的位置向量平行，故有：

\frac{\mathrm{d} x}{\mathrm{d} t} \\ \frac{\mathrm{d} y}{\mathrm{d} t} \end{array}\right)=\lambda\left(\begin{array}{l} X-x \\ Y-y \end{array}\right), \quad \lambda>0(2)$$ 将 $$\left\{\begin{array}{l} \frac{\mathrm{d} x}{\mathrm{d} t}=\frac{w}{\sqrt{(X-x)^{2}+(Y-y)^{2}}}(X-x) \\ \frac{\mathrm{d} y}{\mathrm{d} t}=\frac{w}{\sqrt{(X-x)^{2}+(Y-y)^{2}}}(Y-y) \end{array}\right.(3)$$ 不妨假设乙舰速度为1，则w=5，X=1，Y=t，此时导弹的参数轨迹为： $$\left\{\begin{array}{l} \frac{\mathrm{d} x}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+(t-y)^{2}}}(1-x) \\ \frac{\mathrm{d} y}{\mathrm{d} t}=\frac{5}{\sqrt{(1-x)^{2}+(t-y)^{2}}}(t-y) \\ x(0)=0, y(0)=0 \end{array}\right.$$ matlab求解： ```php function dy=eq2(t,y) dy=zeros(2,1); dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(t-y(2))^2); dy(2)=5*(t-y(2))/sqrt((1-y(1))^2+(t-y(2))^2); end %调用 [t,y]=ode45('eq2',[0 2],[0 0]); Y=0:0.01:2; plot(1,Y,'-') hold on plot(y(:,1),y(:,2),'*') ``` 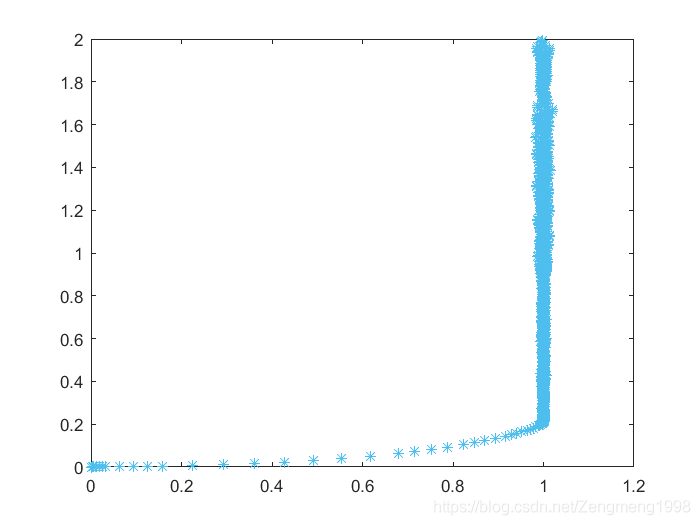 由图可得，导弹最终大致在(1，0.2)处命中目标。这里还以尝试用二分法的思想进一步得到更精确的答案，……tf=0.21是可得求解图像为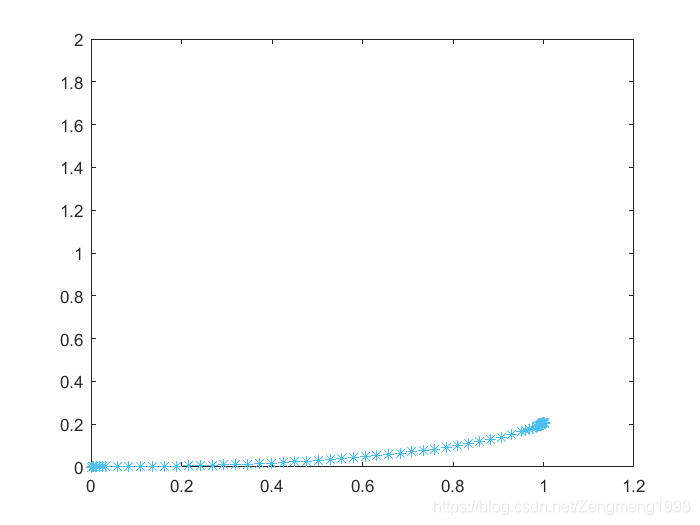：  据此可得更为精确的答案。