AcWing算法基础课 Level-2 第三讲 搜索与图论


单链表

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;// 初始化
void init()
{head = -1;idx = 0;
}// 将x插到头结点
void add_to_head(int x)
{e[idx] = x, ne[idx] = head, head = idx ++ ;
}// 将x插到下标是k的点后面
void add(int k, int x)
{e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}// 将下标是k的点后面的点删掉
void remove(int k)
{ne[k] = ne[ne[k]];
}int main()
{int m;cin >> m;init(); // 初始化while (m -- ){int k, x;char op;cin >> op;if (op == 'H'){cin >> x;add_to_head(x);}else if (op == 'D'){cin >> k;if (!k) head = ne[head];else remove(k - 1);}else{cin >> k >> x;add(k - 1, x);}}for (int i = head; i != -1; i = ne[i]) cout << e[i] << " ";cout << endl;return 0;
}
双链表

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;int idx, l[N], r[N], e[N];//在节点a的右边插入x
void insert(int a, int x)
{e[idx] = x;l[idx] = a, r[idx] = r[a];l[r[a]] = idx, r[a] = idx ++ ;
}//删除节点a
void remove(int a)
{r[l[a]] = r[a];l[r[a]] = l[a];
}int main()
{//0是左端点,1是右端点l[1] = 0, r[0] = 1, idx = 2;int m;cin >> m;while (m -- ){string op;int k, x;cin >> op;if (op == "L"){cin >> x;insert(0, x);}else if (op == "R"){cin >> x;insert(l[1], x);}else if (op == "D"){cin >> k;remove(k + 1);}else if (op == "IL"){cin >> k >> x;insert(l[k + 1], x);}else {cin >> k >> x;insert(k + 1, x);}}for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << " ";return 0;
}
树与图的深度优先遍历
树的重心

- 树是一种特殊的图,无向图又是特殊的有向图;因此考虑有向图如何存储即可;有向图的存储 :稠密图->邻接矩阵;邻接表,存储每个点可以到达哪些点
- 图的邻接表存储方式是为每一个结点开个表,存的意思是从这个点可以走到哪些点,这个单链表内部点的顺序是无关紧要的
- n个点所以是n-1条边;cstring头文件;边数这里设置为点数的两倍,在开数组时注意;st数组记录是否遍历过该点,在遍历一个点所有能到达的点的过程中,为了避免走回头路,也要用到st数组;注意当前这颗子树的大小 和 去掉这个点后最大联通块 之间的关系;图用的是多条单链表,所以注意每次都要初始化h数组;无向图,所以add两次;这里随便挑一个点都可以开始dfs,树从哪个点都可以开始当根
#include <algorithm>
#include <cstring> // memset
#include <iostream>using namespace std;const int N = 1e5 + 10, M = 2 * N;int n, m;// head, e[M],ne[M],idx; 是一条单链表
// h[N], e[M],ne[M],idx; 是N条单链表
int h[N], e[M], ne[M], idx;bool st[N]; // 用st数组存一下哪些点已经被遍历过了int ans = N; //记录一个全局最大值// 在a对应的单链表中插入一个节点b
void add(int a, int b)
{e[idx] = b; // 表示第idx条边指向b点ne[idx] = h[a]; // ne[idx]表示第idx条边的下一条边是 a点的邻接链表的第一条边h[a] = idx++; // head[a]表示将a点的邻接链表的第一条边更新为第idx条边
}// u表示当前已经dfs到的这个点
// 以u为根的子树中, 点的数量
int dfs(int u)
{st[u] = true; // 标记一下, 当前这个点已经被搜索过int sum = 1; // 记录当前子树大小int res = 0; // 把u这个点删除之后, 每一个联通块的最大值for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i]; // 当前这个链表中的节点, 对应图中的点的编号是多少if (!st[j]) {int s = dfs(j); // j这棵子树的大小res = max(res, s); //最大的联通块大小sum += s;}}res = max(res, n - sum);ans = min(ans, res);return sum;
}int main()
{// 一条单链表 head初始化为-1// n条单链表,把所有的head初始化为-1memset(h, -1, sizeof h);cin >> n;for (int i = 0; i < n - 1; i++) {int a, b;cin >> a >> b;add(a, b);add(b, a);}// 随便挑一个点, 比方说从第一个点开始搜dfs(1);cout << ans << endl;return 0;
}
树与图的广度优先遍历
图中点的层次

- 建图然后bfs;dist表示距离,-1表示走不到,初始化为-1
#include <iostream>
#include <cstring>
#include <queue>using namespace std;const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;
int dist[N];void add(int a, int b)
{e[idx] = b;ne[idx] = h[a];h[a] = idx ++ ;
}int bfs()
{memset(dist, -1, sizeof dist);queue<int> q;q.push(1);dist[1] = 0;while (q.size()){auto t = q.front();q.pop();for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (dist[j] == -1){dist[j] = dist[t] + 1;q.push(j);}}}return dist[n];
}int main()
{memset(h, -1, sizeof h);scanf("%d%d", &n, &m);for (int i = 0; i < m; i ++ ){int a, b;scanf("%d%d", &a, &b);add(a, b);}printf("%d\n", bfs());
}拓扑排序
有向图的拓扑序列

- 有向无环图也被称为拓扑图
- 拓扑序列 :所有的边都从前指向后,那么所有入度为0的点都可以作为起点
#include <iostream>
#include <cstring>
#include <queue>using namespace std;const int N = 1e5 + 10;int h[N], e[N], ne[N], idx;
int top[N];
int d[N];
int cnt = 0;
int n, m;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool topsort()
{queue<int> q;for (int i = 1; i <= n; i ++ )if (!d[i])q.push(i);while (q.size()){auto t = q.front();q.pop();top[cnt ++ ] = t;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];d[j] -- ;if (!d[j])q.push(j);}}return cnt == n;
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);for (int i = 0; i < m; i ++ ){int a, b;cin >> a >> b;add(a, b);d[b] ++ ;}if (!topsort()) puts("-1");else{for (int i = 0; i < n; i ++ ){cout << top[i];if (i != n - 1) cout << ' ';}}return 0;
}#include <iostream>
#include <cstring>using namespace std;const int N = 1e5 + 10;int h[N], e[N], ne[N], idx;
int q[N];
int d[N];int n, m;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool topsort()
{int hh = 0, tt = -1;for (int i = 1; i <= n; i ++ )if (!d[i])q[ ++ tt] = i;while (hh <= tt){auto t = q[hh ++ ];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];d[j] -- ;if (!d[j])q[ ++ tt] = j;}}return tt + 1 == n;
}int main()
{memset(h, -1, sizeof h);cin >> n >> m;for (int i = 0; i < m; i ++ ){int a, b;cin >> a >> b;add(a, b);d[b] ++ ;}if (!topsort()) puts("-1");else{for (int i = 0; i < n; i ++ ){cout << q[i];if (i != n - 1) cout << ' ';}}return 0;
}Dijkstra
Dijkstra求最短路 I

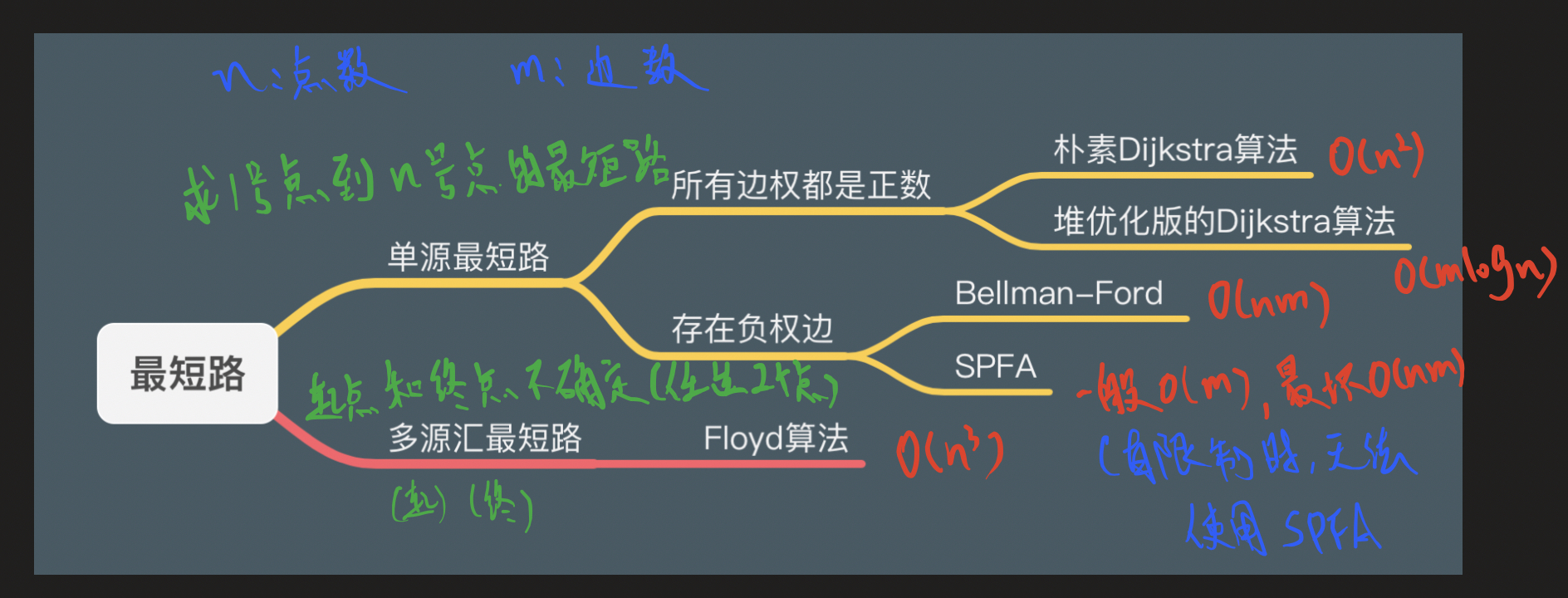
- 稠密图,邻接矩阵;稀疏图,邻接表
- 建图时要把所有边初始化为正无穷,,为了应对重边,每次保留最短的边;先将所有距离初始化为正无穷,起点距离为0,遍历n-1轮,每轮确定一个点,找到未标记的点中距离最小的,然后用这个点更新其它点的距离,再标记这个距离最小的点,表示已经用它更新过
- 每个点只能被用来更新其它点一次
- 基于贪心思想,只适用于所有边的长度都是非负数的图
#include <iostream>
#include <cstring>using namespace std;const int N = 510;int g[N][N];
int dist[N];
bool st[N];int n, m;int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]);st[t] = true;}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main()
{memset(g, 0x3f, sizeof g);cin >> n >> m;for (int i = 0; i < m; i ++ ){int a, b, c;cin >> a >> b >> c;g[a][b] = min(g[a][b], c);}printf("%d", dijkstra());return 0;
}Dijkstra求最短路 II

- 稀疏图 -> 邻接表(相比多了w数组记录权值
- 用邻接表存图,重边无所谓
- priority_queue在queue头文件中,小根堆默认按照第一个权值从小到大排序
- 小根堆的写法
- 每次找全局最小且未被标记过的去更新其它点的dist;所以在每次更新的时候顺便把新的dist和对应的点放进去
- 同上,每一个点只会被用来松弛其它边一次,所以只会进优先队列一次;在松弛其它边的时候,如果松弛成功,就将点进入优先队列
#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>using namespace std;const int N = 1e6 + 10;typedef pair<int, int> pii;int n, m;
int head[N], e[N], ne[N], idx, w[N];
int dist[N]; //从1号点走到每个点, 当前的最短距离是多少
bool st[N]; //用于在更新最短距离时,判断当前的点的最短距离是否确定,是否需要更新void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = head[a];head[a] = idx++;
}// 进行n次迭代后最后就可以确定每个点的最短距离
// 然后再根据题意输出相应的 要求的最短距离
int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0; // 第一个点到自己的距离为0priority_queue<pii, vector<pii>, greater<pii>> heap; //转换为小根堆heap.push({0, 1}); //将1号点放进来, 值是0, 编号是1while (heap.size()) {auto t = heap.top(); //每次找到堆中最小的点heap.pop();int ver = t.second, distance = t.first; //距离最小的点的编号和距离if (st[ver]) { //如果这个点被访问过, 就continuecontinue;}st[ver] = true;// 更新当前这个点的所有出边for (int i = head[ver]; i != -1; i = ne[i]) {int j = e[i];if (dist[j] > distance + w[i]) {dist[j] = distance + w[i];heap.push({dist[j], j});}}}if (dist[n] == 0x3f3f3f3f) { // 如果第n个点路径为无穷大即不存在最低路径return -1;}return dist[n];
}int main()
{cin >> n >> m;memset(head, -1, sizeof head);for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add(a, b, c); //用邻接表存, 重边就无所谓了}// 求单源最短路径cout << dijkstra() << endl;return 0;
}
bellman-ford
有边数限制的最短路

- memcpy(last, dist, sizeof dist)中last数组是上一轮中dist数组的备份,是为了防止串联更新,因为bellmanford是求有边数限制的最短路,而spfa是没有边数限制的,所以不需要拷贝上一轮。
- Bellman - ford 算法是求含负权图的单源最短路径的一种算法,效率较低,代码难度较小。其原理为连续进行松弛,在每次松弛时把每条边都更新一下,若在 n-1 次松弛后还能更新,则说明图中有负环,因此无法得出结果,否则就完成。
- 在下面代码中,是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断,而并非是if(dist[n] == INF)判断,原因是INF是一个确定的值,并非真正的无穷大,会随着其他数值而受到影响,dist[n]大于某个与INF相同数量级的数即可
- bellman - ford算法擅长解决有边数限制的最短路问题,时间复杂度 O(nm),其中n为点数,m为边数
- 存边方式独特,边数限制,拷贝上一轮,大于判断
#include <algorithm>
#include <cstring>
#include <iostream>using namespace std;const int N = 510, M = 10010;struct Edge
{int a, b, c;
} edges[M];int n, m, k;
int dist[N];
int last[N];void bellman_ford()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; i++) {memcpy(last, dist, sizeof dist); //只用上一次迭代的结果for (int j = 0; j < m; j++) {auto e = edges[j];dist[e.b] = min(dist[e.b], last[e.a] + e.c);}}
}int main()
{cin >> n >> m >> k;for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;edges[i] = {a, b, c};}bellman_ford();if (dist[n] > 0x3f3f3f3f / 2) {cout << "impossible" << endl;}else {cout << dist[n] << endl;}return 0;
}
spfa
spfa求最短路

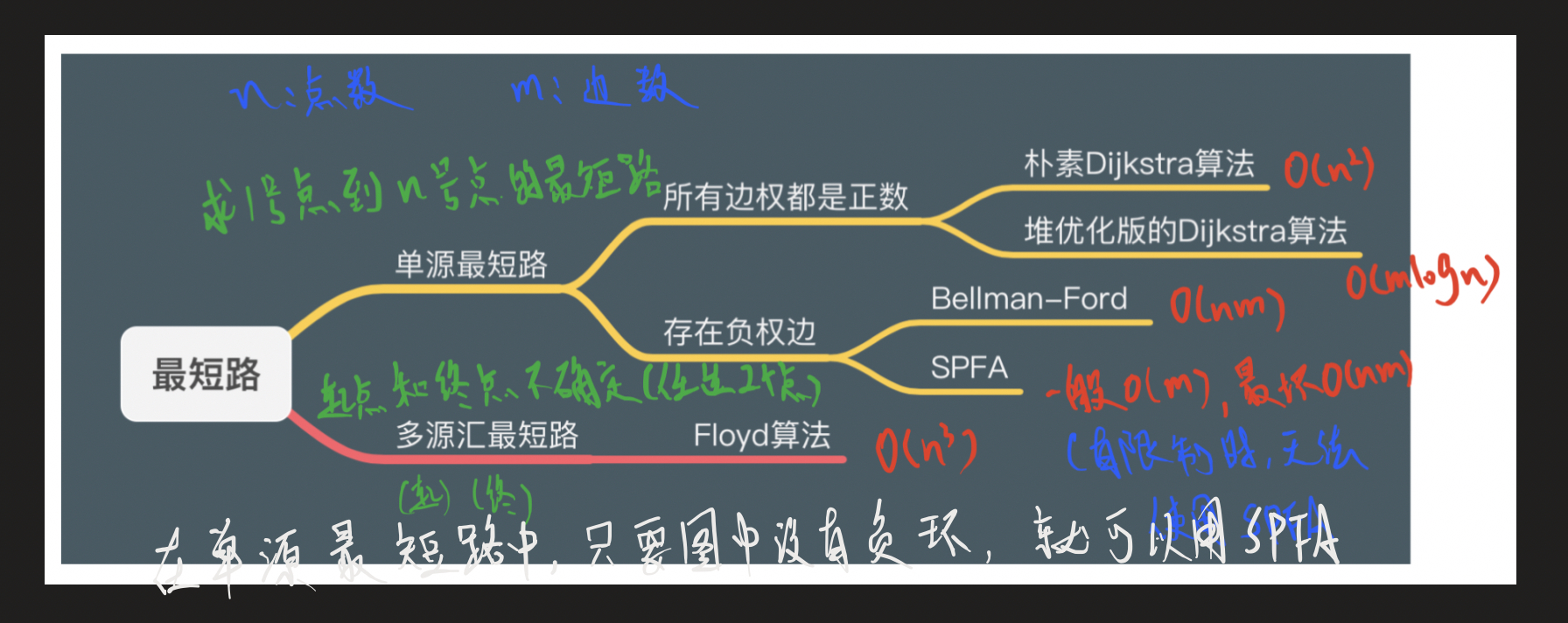
- spfa被称为队列优化的bellmanford算法,
- 建立一个队列,最初队列中只包含起点;取出队头x,扫描它的所有出边(x,y,z),如果能被松弛,则松弛dist[y],同时如果y不在队列中,将y放入队列中(每次取出队头的时候也要改变st数组);
- 一个结点可能被入队,出队多次;这个队列避免了bellmanford算法中对不需要拓展的结点的冗余扫描,在稀疏图上运行效率较高,为O(km)O(km)O(km)级别,k是一个较小的常数,但在稠密图或者特殊构造的网格图上,仍可能退化成O(nm)O(nm)O(nm)
- st为true的点也可能被再次更新,所以更新的时候不需要判断是否!st
- st数组记录这个点当前是否在队列中
- 队列中都是由起点更新到的点,不存在bellmanford中未更新到的点同样被边更新的情况,所以spfa中等于判断就可以,不像bellman中是大于判断
#include <cstring>
#include <iostream>
#include <queue>using namespace std;const int N = 1e5 + 10;int n, m;
int head[N], e[N], ne[N], w[N], idx;
bool st[N];
int dist[N];void add(int a, int b, int c)
{e[idx] = b;w[idx] = c;ne[idx] = head[a];head[a] = idx++;
}int spfa()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;queue<int> q;q.push(1);st[1] = true; //判重数组, 队列中有重复的点没有意义while (q.size()) {int t = q.front();q.pop();st[t] = false;for (int i = head[t]; i != -1; i = ne[i]) {int j = e[i];if (dist[j] > dist[t] + w[i]) {dist[j] = dist[t] + w[i];if (!st[j]) {q.push(j);st[j] = true;}}}}if (dist[n] == 0x3f3f3f3f) {return -1;}return dist[n];
}int main()
{cin >> n >> m;memset(head, -1, sizeof head);for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add(a, b, c);}int t = spfa();if (t == -1) {cout << "impossible" << endl;}else {cout << dist[n] << endl;}return 0;
}
spfa判断负环

- dist和cnt数组都不需要被初始化,dist数组代表当前从1到x的最短路径长度,cnt数组代表当前从1到x的边的数量
- 一开始就把所有点都放到队列里,只有在松弛的时候才会判断如果不在队列中再把它放入队列中,如果松弛时发现cnt也就是边数>=n,说明点大于n,说明有负权回路
#include <cstring>
#include <iostream>
#include <queue>using namespace std;const int N = 2e3 + 10, M = 1e4 + 10;int n, m;
int head[N], e[M], ne[M], w[M], idx;
bool st[N];
int dist[N]; // 表示 当前从1 -> x的最短距离
int cnt[N]; //cnt[x] 表示 当前从1 -> x的最短路的边数void add(int a, int b, int c)
{e[idx] = b;ne[idx] = head[a];w[idx] = c;head[a] = idx++;
}bool spfa(){// 这里不需要初始化dist数组为 正无穷/初始化的原因是, 如果存在负环, 那么dist不管初始化为多少, 都会被更新queue<int> q;//不仅仅是1了, 因为点1可能到不了有负环的点, 因此把所有点都加入队列for(int i=1;i<=n;i++){q.push(i);st[i]=true;}while(q.size()){int t = q.front();q.pop();st[t]=false;for(int i = head[t];i!=-1; i=ne[i]){int j = e[i];if(dist[j]>dist[t]+w[i]){dist[j] = dist[t]+w[i];cnt[j] = cnt[t]+1;if(cnt[j]>=n){ // 有n条边,则n + 1个点,抽屉原理,有两个点是同一个点,则说明路径上存在环,又因为路径变小,说明存在负环return true;}if(!st[j]){q.push(j);st[j]=true;}}}}return false;
}int main()
{cin >> n >> m;memset(head, -1, sizeof head);for (int i = 0; i < m; i++) {int a, b, c;cin >> a >> b >> c;add(a, b, c);}if (spfa()) {cout << "Yes" << endl;}else {cout << "No" << endl;}return 0;
}
Floyd
Floyd求最短路

- D[k, i, j]表示“经过若干个编号不超过k的结点“从i到j的最短路径,该问题可划分为两个子问题,经过编号不超过k-1的点从i到j,或者从i先到k再到j,D[k,i,j]=min(D[k−1,i,j],D[k−1][i][k]+D[k−1][k][j])D[k,i,j]=min(D[k-1,i,j],D[k-1][i][k]+D[k-1][k][j])D[k,i,j]=min(D[k−1,i,j],D[k−1][i][k]+D[k−1][k][j]),初值为D[0,i,j]=A[i,j]D[0,i,j]=A[i,j]D[0,i,j]=A[i,j],其中A[i,j]是开头定义的邻接矩阵
- 与背包问题的状态转移方程类似,k这一维可被省略D[i,j]=min(D[i,j],D[i][k]+D[k][j])D[i,j]=min(D[i,j],D[i][k]+D[k][j])D[i,j]=min(D[i,j],D[i][k]+D[k][j]),最终D[i][j]就保存了从i到j的最短路长度
#include <algorithm>
#include <cstring>
#include <iostream>using namespace std;const int N = 210, INF = 1e9;int n, m, Q;
int d[N][N];void floyd()
{for (int k = 1; k <= n; k++) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}
}int main()
{cin >> n >> m >> Q;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) {d[i][j] = 0;}else {d[i][j] = INF;}}}while (m--) {int a, b, c;cin >> a >> b >> c;d[a][b] = min(d[a][b], c);}floyd();while (Q--) {int a, b;cin >> a >> b;int t = d[a][b];if (t > INF / 2) {cout << "impossible" << endl;}else {cout << t << endl;}}return 0;
}- floyd距离和邻接矩阵中两点之间边的距离用的是同一个数组,
- 这里也可以用0x3f3f3f3f,之所以能用1e9应该是这里的总边长才2e8
- 邻接矩阵的初始化,这里多了个0,值得注意
- 这里仍然是判断大于而不是判断等于,也许还是因为不是从起点更新起的,
Prim
Prim算法求最小生成树

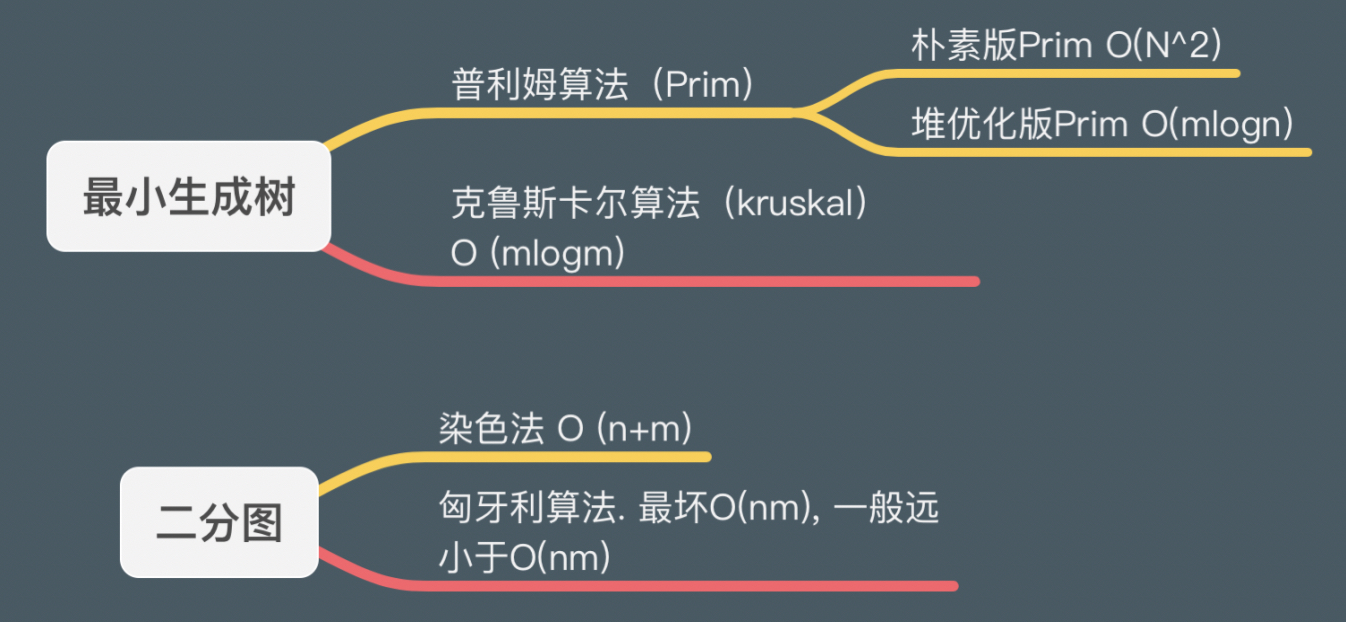
- O(n2)O(n^2)O(n2)。堆优化版也不如kruskal方便,所以Prim算法主要用于稠密图,尤其是完全图的最小生成树的求解。
- Prim总是维护最小生成树的一部分。最初,Prim算法仅确定1号节点属于最小生成树;把元素从剩余节点集合中删除,加入到已经属于最小生成树的节点集合中去,并把两个端点分别属于这两个集合中的权值最小的点累加到答案中。
- 可以类别Dijkstra,用一个数组标记节点是否属于集合T,每次从未标记的节点中选择d值最小的,把它标记,同时扫描所有出边,更新另一个端点的d值。
#include <iostream>
#include <cstring>using namespace std;const int N = 510;
const int INF = 0x3f3f3f3f;int g[N][N];
int dist[N];
bool st[N];
int n, m;int prim()
{memset(dist, 0x3f, sizeof dist);int res = 0;dist[1] = 0;for (int i = 0; i < n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;if (i && dist[t] == INF) // 如果i为0不用return INF;st[t] = true; // 标记if (i) res += dist[t]; // 如果i为0不用累加for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], g[t][j]); // 是与g做比较,因为t已经是最小生成树里的了}// 返回累加答案return res;
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);while (m -- ){int u, v, w;cin >> u >> v >> w;g[u][v] = g[v][u] = min(g[u][v], w);}int t = prim();if (t == INF) puts("impossible");else cout << t << endl;return 0;
}Kruskal
Kruskal算法求最小生成树

- 从边带权的无向图中选n个点和n-1条本来就有的边构成的无向连通子图称为生成树,在此基础上边的权值之和最小的称为最小生成树
- 定理 :任意一颗最小生成树一定包含无向图中权值最小的边
- Kruskal算法总是维护无向图的最小生成森林
- 在任意时刻,Kruskal算法从剩余的边中选一条权值最小的,并且这条边的两个端点属于生成森林中两颗不同的树(不连通),把该边加入该森林。图中节点的连通情况可以用并查集维护
- 流程 :建立并查集;把所有边按权值排序从小到大,依次扫描每条边;若两个端点属于同一个集合,则忽略这条边;否则,合并两个端点所在的集合,并将权值累加到答案中
- 虽然Kruskal算法的时间复杂度局限在于它第一步要使用的库里的快排,o(mlog(m)),但快排常数非常小,所以Kruskal很快
#include <iostream>
#include <algorithm>using namespace std;const int N = 1e5 + 10, M = 2e5 + 10, INF = 0x3f3f3f3f;
int n, m;
int fa[N];struct Edge
{int a, b, w;bool operator< (const Edge &W) const{return w < W.w;}
}edges[M];int find(int x)
{if (fa[x] != x) fa[x] = find(fa[x]);return fa[x];
}int kruskai()
{for (int i = 1; i <= n; i ++ ) fa[i] = i; // 初始化并查集int res = 0, cnt = 0;1for (int i = 0; i < m; i ++ ){int a = edges[i].a, b = edges[i].b, w = edges[i].w;a = find(a), b = find(b);if (a != b){res += w;cnt ++ ;fa[a] = b;}}if (cnt < n - 1) return INF;return res;
}int main()
{cin >> n >> m;for (int i = 0; i < m; i ++ )cin >> edges[i].a >> edges[i].b >> edges[i].w;sort(edges, edges + m); // 排序int t = kruskai();if (t == INF)puts("impossible");elsecout << t;return 0;
}染色法判定二分图
染色法判定二分图

- 二分图 :当且仅当图中没有奇数环,划分为两个集合,集合内部没有边
#include <iostream>
#include <algorithm>
#include <cstring>using namespace std;const int N = 1e5 + 10, M = 2 * N; // 无向图,边存两次,数组两倍int h[N], e[M], ne[M], idx;
int co[N];
int n, m;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool dfs(int u, int c)
{co[u] = c;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (!co[j] && !dfs(j, 3 - c))return false;else if (co[j] == c)return false;}return true;
}int main()
{memset(h, -1, sizeof h);cin >> n >> m;for (int i = 0; i < m; i ++ ){int u, v;cin >> u >> v;add(u, v);add(v, u); // 无向图}bool success = true;for (int i = 1; i <= n; i ++ ) // 图可能不连通if (!co[i] && !dfs(i, 1)){success = false;break;}if (success) puts("Yes");else puts("No");return 0;
}匈牙利算法
二分图的最大匹配

- “任意两条边都没有公共端点”的边的集合被称为图的一组匹配。在二分图中,包含边数最多的一组匹配被称为二分图的最大匹配。
- 二分图的一组匹配S是最大匹配,当且仅当图中不再存在S的增广路

- 匈牙利算法基于贪心思想,当一个点成为匹配点后,最多因为增广路而更换匹配对象,不会再变回非匹配点
- 对于每个左部节点,寻找增广路最多遍历整张二分图一次,所以O(nm)O(nm)O(nm)
#include <iostream>
#include <cstring>using namespace std;const int N = 510, M = 1e5 + 10;int h[N], e[M], ne[M], idx;
bool st[N]; // st数组代表对于当前左部节点,右部的这个节点在它这轮的匹配中是否被“询问”过;在同一轮中不要重复询问同一个点
int match[N];
int n1, n2, m;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}bool find(int x)
{for (int i = h[x]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}int main()
{memset(h, -1, sizeof h);cin >> n1 >> n2 >> m;for (int i = 0; i < m; i ++ ){int a, b;cin >> a >> b;add(a, b);
// add(b, a); 从左部匹配右部,所以即使无向图,加了会wa}int res = 0;for (int i = 1; i <= n1; i ++ ){memset(st, 0, sizeof st);if (find(i)) res ++ ;}cout << res << endl;return 0;
}AcWing算法基础课 Level-2 第三讲 搜索与图论相关推荐
- Acwing《算法基础课》第3章 搜索与图论
Acwing<算法基础课>第3章 搜索与图论 文章目录 Acwing<算法基础课>第3章 搜索与图论 深度优先遍历DFS 宽度优先搜索BFS 拓扑排序 dijkstra算法 朴 ...
- AcWing基础算法课Level-2 第三讲 搜索与图论
AcWing基础算法课Level-2 第三讲 搜索与图论 DFS AcWing 842. 排列数字3379人打卡 AcWing 843. n-皇后问题3071人打卡 BFS AcWing 844. 走 ...
- 算法与数据结构模版(AcWing算法基础课笔记,持续更新中)
AcWing算法基础课笔记 文章目录 AcWing算法基础课笔记 第一章 基础算法 1. 排序 快速排序: 归并排序: 2. 二分 整数二分 浮点数二分 3. 高精度 高精度加法 高精度减法 高精度乘 ...
- 背包四讲 (AcWing算法基础课笔记整理)
背包四讲 背包问题(Knapsack problem)是一种组合优化的NP完全问题.问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高 ...
- ACwing算法基础课全程笔记(2021年8月12日开始重写+优化)
更好的阅读体验 ※基础模板 2021年8月12日开始对基础课笔记进行重写+优化 请大家支持AcWing正版,购买网课能让自己获得更好的学习体验哦~ 链接:https://www.acwing.com/ ...
- Acwing算法基础课学习笔记
Acwing学习笔记 第一章 基础算法 快速排序 归并排序 二分查找 前缀和与差分 差分 位运算 离散化 第二章 数据结构 单链表 双链表 栈 队列 单调栈 单调队列 KMP算法 Trie 并查集 堆 ...
- AcWing算法基础课 第一讲小结(持续更新中)
目录 前言 一.快速排序法及其扩展 快速排序法 介绍 思路 + 步骤 模拟代入 模板 练习 扩展(求第k个数) 思路 代码 二.归并排序法 归并排序 思路 思路 + 步骤 模拟代入 模板 练习 应用( ...
- Acwing - 算法基础课 - 笔记(图论 · 三)
文章目录 搜索与图论(三) 最小生成树 Prim算法 Kruskal算法 总结 二分图 染色法 匈牙利算法 小结 搜索与图论(三) 这一节讲解的是最小生成树和二分图 最小生成树 什么是最小生成树?首先 ...
- 【模板】ACwing算法基础课模板小全
一.基础算法 快速排序算法模板 void quick_sort(int q[], int l, int r) {//递归的终止情况if (l >= r) return;//选取分界线.这里选数组 ...
- AcWing 算法基础课第三节基础算法3 双指针、位运算、离散化、区间合并
1.该系列为ACWing中算法基础课,已购买正版,课程作者为yxc 2.y总培训真的是业界良心,大家有时间可以报一下 3.为啥写在这儿,问就是oneNote的内存不够了QAQ ACwing C++ 算 ...
最新文章
- python属性和局部变量_python类与对象1
- java泛型数组替代方案_Kotlin泛型Array T导致“不能将T用作具体类型参数 . 使用类代替“但List T不会...
- python的赋值与参数传递(python和linux切换)
- css动画详解 (transition animation)
- Delphi TXLSReadWriteII导出Excel
- CREO 6.0 - 基础 - 01 - 零件 - 零件的装配 - 零件的移动、偏转、角度角度设定
- 潭州课堂25班:Ph201805201 爬虫高级 第三课 sclapy 框架 腾讯 招聘案例 (课堂笔记)...
- mysql scale,Mailchimp Scale:a MySQL Perspective
- sql2005数据库备份—sql语句
- python MySQLdb安装和使用
- 转载:ASP.net页面跳转方式三种
- 基于Java的webapp_第一个 JAVA WEB 应用
- 第十届蓝桥杯 省赛研究生组 真题解析(Python)
- 新浪微博 android2.3,BlackLight新浪微博客户端
- Python — — turtle 常用代码
- JavaSE数组基础练习题
- Android自定义组件之日历控件-精美日历实现(内容、样式可扩展)
- CSS实现空心三角指示箭头
- EC esayClick 自定义浮窗
- 知名云计算厂商云宏加入龙蜥社区,共同打造信息安全坚实“地基”
