title: 图论期末考试复习
date: 2020-08-24 09:01:09
tags:

参考资料：《图论及其应用》高等教育出版社张先迪 / 李正良
仅用于复习参考，公式或多有误，请以教材为准。

文章目录

- title: 图论期末考试复习 date: 2020-08-24 09:01:09 tags:
引言
**第一章图的基本概念**
- 图与简单图
- - 图的定义及其相关概念
  - 图的同构
  - - 作业题P29—P30 3, 4, 5, 6
- 完全图偶图与补图
- - 定理1：若n阶图G是自补图，则有：![在这里插入图片描述](https://img-blog.csdnimg.cn/20200821152034295.png#pic_center)
- 顶点的度与图的度序列
- - - **定理2 握手定理** 图G= (V, E)中所有顶点的度的和等于边数m的2倍，即：
  - 图的度序列及其性质
  - - 定理3 非负整数组(d1,d2,…., d n)是图的度序列的充分必要条件是序列中元素总和为偶数。
  - 图序列及其性质
  - - 定理4 非负整数组
    - 定理5 (厄多斯1960) 非负整数组
    - 定理6 一个**简单图**G的n个点的度不能互不相同.
    - 定理7 一个n阶图G和它的**补图有相同的频序列**。
    - 作业 P29—P30 8, 9, 10, 11
- 子图与图运算
- - 子图的相关概念
  - - 定理1 简单图G=(n, m) 的所有生成子图个数为2^m.
  - **图运算**
- 路与连通性
- - 路与圈的相关概念
  - 连通性相关概念
  - - 连通性性质
    - 定理1：若图G不连通，则其补图连通。
  - 偶图的判定定理
  - - 定理2 一个图是偶图当且当它不包含奇圈。
    - 作业 P29—P30 13, 14, 20, 22
- 最短路及其算法
- - 最短路应用
  - - 作业 P29—P30 16
- 图的代数表示及其特征
- - 图的邻接矩阵
  - - 定理1 设 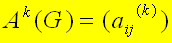![在这里插入图片描述](https://img-blog.csdnimg.cn/20200821170719510.png#pic_center)，则aij(k)a_{ij}^{(k)}aij(k)表示顶点vi到顶点vj的途径长度为k的途径条数。
  - 图的关联矩阵
- 极图
- - 邻接谱、邻接代数与图空间
  - 托兰定理
  - - 定理6 若n阶简单图G不包含Kl+1K_{l+1}Kl+1，则G度弱于某个完全 l 部图 H，且若G具有与 H 相同的度序列，则: ![在这里插入图片描述](https://img-blog.csdnimg.cn/20200821174340874.png#pic_center)
    - 定理7（Turán）若G是简单图，并且不包含 Kl+1K_{l+1}Kl+1,则：m(G)≤m(Tl,n)m(G) \leq m(T_{l,n})m(G)≤m(Tl,n)
    - 不含子图H(Kl+1K_{l+1}Kl+1)最多边数：m(n,Kl+1)=(l−1)(n2−r2)/(2l)+C(r,2)m(n,K_{l+1}) = (l-1)(n^2-r^2)/(2l)+C(r,2)m(n,Kl+1)=(l−1)(n2−r2)/(2l)+C(r,2)
    - 连通偶图的2部划分是唯一的
**第二章树**
- 树的概念与性质
- - - 定理1 每棵非平凡树至少有两片树叶。
    - 定理2 图G是树当且仅当G中任意两点都被唯一的路连接。
  - 定理3 设T是(n, m)树，则：m=n−1m = n - 1m=n−1
  - - 推论1 具有k个分支的森林有n-k条边。
    - 定理4 每个n阶**连通**图的边数至少为n-1.
    - 定理5 任意树T的两个不邻接顶点之间添加一条边后，可以得到**唯一圈**。
    - 定理6 设S=｛d1,d2,…,dn｝是n个正整数序列，它们满足：d1≧d2≧…≧dn ,∑di=2(n-1).则存在一颗树T，其度序列为S。
- 树的中心与形心
- - 定理7 每棵树的中心由一个点或两个相邻点组成。
  - 定理8 每一棵树有一个由一个点或两个邻接的点组成的形心。
  - 作业 P43 习题2 ： 1，2，3，4，5，6
- 生成树
- - 生成树的概念与性质
  - - 定理1 每个**连通图**至少包含一棵生成树。
  - 生成树的计数
  - - 凯莱递推计数法
    - 定理2 (**Cayley**) 设e是G的一条边，则有：τ(G)=τ(G−e)+τ(Ge)\tau (G) = \tau (G - e) + \tau (Ge)τ(G)=τ(G−e)+τ(Ge)
    - 关联矩阵计数法
    - 定理3 设Am是连通图G的基本关联矩阵的**主子阵**，则Am**非奇异**的充分必要条件是相应于Am的列的那些边构成G的一棵生成树。
    - 矩阵树定理
    - 定理4 (矩阵树定理) 设G是顶点集合为V(G)=｛v1,v2,…,vn｝,的图，设A=(aij)是G的邻接矩阵，C=(cij)是n阶方阵，其中：
  - 回路系统简介
  - - 定理4 设T是连通图G=(n, m) 的一棵生成树,C1, C2,…,Cm-n+1是G对应于T的基本回路组。定义：1.Gi=Gi , 0.Gi=Φ,Gi是G的回路。则G的回路组作成的集合对于该乘法和图的对称差运算来说作成数域F=｛0,1｝上的m-n+1维向量空间。
    - P43 习题2 ： 12, 14, 15
- 最小生成树
- - 克鲁斯克尔算法
  - 管梅谷的破圈法
  - Prim算法
  - 根树简介
  - - 定理2 在完全m元树T中，若树叶数为t , 分支点数为i , 则：(m−1)i=t−1(m - 1)i = t - 1(m−1)i=t−1
    - P43 习题2 ： 16, 17, 18
**第三章图的连通度**
- 割边，割点和块
- - 割边及其性质
  - - 定理1 边 e 是图G的割边当且仅当 e 不在G的任何圈中。
    - 推论1 e为连通图G的一条边，如果e含于G的某圈中，则G-e连通。
  - 割点及其性质
  - - 定理2 G**无环且非平凡**，则v是G的割点，当且仅当ω(G−v)>ω(G)\omega (G - v) > \omega (G)ω(G−v)>ω(G)
    - 定理3 v 是树T的顶点，则v是割点，当且仅当v是树的分支点。
    - 定理4 设v是无环连通图G的一个顶点，则v是G的割点，当且仅当V(G-v)可以划分为两个非空子集V1与V2,使得对任意x ∈V1, y ∈V2, 点v在每一条x y路上。
  - 块及其性质
  - - 定理5 若|V(G)|≧3,则G是块，当且仅当G无环且任意两顶点位于同一圈上。
    - 定理6 点v是图G的割点当且仅当v至少属于G的两个不同的块。
    - P65---66 习题3 ： 1, 2, 3,5,7,8
- 连通度
- - 连通度的概念与性质
  - - 点连通度与边连通度的概念
    - 连通度的性质
    - 定理1 (惠特尼1932) 对任意图G，有：k(G)≤λ(G)≤δ(G)k(G) \le \lambda (G) \le \delta (G)k(G)≤λ(G)≤δ(G)
    - 定理2 设G是**(n, m)连通图**，则：k(G)≤⌊2mn⌋k(G) \le \left\lfloor {{{2m} \over n}} \right\rfloor k(G)≤⌊n2m⌋
    - 哈拉里图:涉及可靠性通信网络构建
    - 定理3 设G是(n, m)单图，若$\delta (G) \ge \left\lfloor {{{\rm{n}} \over {\rm{2}}}} \right\rfloor $，则**G连通。**
    - 定理4 设G是(n, m)单图，若对任意正整数k ,有：δ(G)≥n+k−22\delta (G) \ge {{n + k - 2} \over 2}δ(G)≥2n+k−2则G是k连通的。
    - 定理5 设G是n阶单图，若δ(G)≥⌊n2⌋\delta (G) \ge \left\lfloor {{n \over 2}} \right\rfloor δ(G)≥⌊2n⌋则有：λ(G)=δ(G)\lambda (G) = \delta (G)λ(G)=δ(G)
    - P66---67 习题3 ： 1 2, 13, 14, 20
  - 描述连通性的其它参数简介(内容拓展)
  - 敏格尔定理
  - - 定理1 (敏格尔1902---1985) (1) 设x与y是图G中的两个不相邻点，则G中分离点x与y的最少点数等于独立的(x, y)路的最大数目；
    - 定理2 (惠特尼1932) 一个非平凡的图G是k (k≧2)连通的，当且仅当G的任意两个顶点u与v间，至少存在**k条内点不交的(u ,v)路。**
    - 定理3 (惠特尼1932) 一个非平凡的图G是k (k≧2)边连通的，当且仅当G的任意两个顶点间至少存在**k条边不重的(u ,v)路**。
    - 推论对于一个阶至少为3的无环图G，下面三个命题等价。
第一次上交作业
**第四章欧拉图与Hamilton图**
- 欧拉图及其性质
- - 欧拉图的性质
  - - **定理一** 下列陈述对于**非平凡连通图G**是等价的
    - **推论1** 连通图G是欧拉图**当且仅当**G的**顶点度数为偶。**
    - **推论2** 连通非欧拉图G存在欧拉迹当且仅当G中**只有两个顶点度数为奇数**。
    - **例题**：
    - 其他性质：
  - **例题3** **（未弄懂）
  - Fleury(夫勒里)算法 (求一条具体欧拉环游的方法)
- 中国邮路问题
- - **求最优环游**：
- Hamilton图
- - 哈密尔顿图的概念
  - 性质与判定
  - - **定理1（必要条件）** 若G是**H图**，则对于V的每个非空真子集S，均有ω(G−S)≤∣S∣ω(G-S)≤|S|ω(G−S)≤∣S∣ 。
    - **定理2** 若图G包含**哈密尔顿路**，则对V(G)的每个真子集S，ω(G−S)≤∣S∣+1。ω(G-S) ≤ |S|+1。ω(G−S)≤∣S∣+1。
    - **定理3（充分条件）** **(Dirac 1952)** 对于n≥3的**简单图**G，如果G中有：δ(G)≥n/2\delta (G) \geq n/2δ(G)≥n/2 则G是H图
    - **定理4（充分条件）** **(Ore 1962)** 对于n≥3的简单图G，如果G中的任意两个不相邻顶点u与v，有：d(u)+d(v)≥nd(u)+d(v)\geq nd(u)+d(v)≥n 则G是H图
    - **闭图与闭包基本概念**
    - **邦迪——闭包定理（充要条件）** 图G是H图**当且仅当**它的闭包是H图。
    - **定理5(Chvátal——度序列判定法)** 设简单图G的度序列是(d1,d2,…,dn), 这里，d1≦d2≦…≦dn,并且n≧3.若**对任意的m

引言

第一章图的基本概念

图与简单图

图的定义及其相关概念

定义1：一个图是一个序偶<V,E>，记为G=(V,E),其中：
- (1) V是一个有限的非空集合，称为顶点集合,其元素称
- 为顶点或点。用|V|表示顶点数；
  (2) E是由V中的点组成的无序对构成的集合，称为边集，
  其元素称为边，且同一点对在E中可以重复出现多次。用
  |E|表示边数。
相关概念
- 有限图：顶点集和边集都有限的图称为有限图。
- 平凡图与空图：只有一个顶点的图称为平凡图；只有点
  没有边的图称为空图。
- n阶图：顶点数为n的图，称为n阶图。
- (n, m) 图：顶点数为n的图，边数为m的图称为(n, m) 图。
- 边的重数：连接两个相同顶点的边的条数称为边的重
  数；重数大于1的边称为重边。
- 环：端点重合为一点的边称为环。
- 简单图：无环无重边的图称为简单图；其余的图称为
  复合图。
- 顶点u与v相邻接：顶点u与v间有边相连接(u adjv)；其中
  u与v称为该边的两个端点。
- 顶点u与边e相关联：顶点u是边e的端点。
- 边e1与边e2相邻接：边e1与边e2有公共端点。

图的同构

定义2：设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点
集合间存在双射，使得边之间存在如下关系：u1,v1$ \in $ V1,
u2,v2$ \in V2，设u1↔u2，v1↔v2,;u1v1V2 ，设u1↔u2，v1↔v2,; u1v1V2，设u1↔u2，v1↔v2,;u1v1 \in $E1 当且仅当u2v2 $ \in E2,且u1v1与u2v2的重数相同。称G1与G2同构，记为：E2, 且u1v1与u2v2的重数相同。称G1与G2同构，记为：E2,且u1v1与u2v2的重数相同。称G1与G2同构，记为：G1≅G2{G_1} \cong {G_2}G1≅G2$
1、图同构的两个必要条件： (1) 顶点数相同；(2) 边数相同。
例3 下面两图同构吗？请给出证明。
- 证明:作映射f : vi ↔ ui
- 容易证明，对∀\forall∀vi v j $ \in E((a)),有f(vi,vj)=uiujE ((a)),有f (v i ,vj) = uiujE((a)),有f(vi,vj)=uiuj \in $E ((b))

作业题P29—P30 3, 4, 5, 6

完全图偶图与补图

完全图
偶图
完全偶图
简单图和补图
自补图
- 定义4 如果图G与其补图同构，则称G为自补图。

定理1：若n阶图G是自补图，则有：

证明

顶点的度与图的度序列

定义5 G的顶点v的度d (v)是指G中与v关联的边的数目，每个环计算两次。

定理2 握手定理图G= (V, E)中所有顶点的度的和等于边数m的2倍，即：

推论1 在任何图中，奇点个数为偶数。
推论2 正则图的阶数和度数不同时为奇数。
例3 Δ与δ是简单图G的最大度与最小度，求证：
证明：握手定理

图的度序列及其性质

定义6 一个图G的各个点的度d1, d2,…, dn构成的非负整数组
(d1, d2,…, dn)称为G的度序列。
1、一个图的度序列与序列中元素排列无关；

定理3 非负整数组(d1,d2,…., d n)是图的度序列的充分必要条件是序列中元素总和为偶数。

证明：
- 必要性：握手定理
- 充分性：构造法（若di为偶数，则在与之对应的点作di/2个环；对于剩下的偶数个奇数，
  顶点画dj-1/2个环。该图的度序列就是已知数组。）

图序列及其性质

定义7 一个非负整数组如果是某简单图的度序列，我们称
它为可图序列，简称图序列。

定理4 非负整数组

是图序列的充分必要条件是：

是图序列。

定理5 (厄多斯1960) 非负整数组

π=(d1,d2,⋯,dn),d1≥d2≥⋯≥dn,∑i=1ndi=2m\pi = ({d_1},{d_2}, \cdots ,{d_n}),{d_1} \ge {d_2} \ge \cdots \ge {d_n},\sum\limits_{i = 1}^n {{d_i} = 2m} π=(d1,d2,⋯,dn),d1≥d2≥⋯≥dn,i=1∑ndi=2m
是图序列的充分必要条件是：

图的频序列及其性质：
- 定义8 设n阶图G的各点的度取s个不同的非负整数
  d1,d2,…, ds。又设度为di的点有bi个 (i = 1,2,…,s)，则故非整数组(b1,b2,…, bs)是n的一个划分，称为G的频序列

定理6 一个简单图G的n个点的度不能互不相同.

注：一个简单图频序列中至少有一个元素大于或等于2。
证明：因为图G为简单图，所以：△(G)≤n-1。鸽笼原理。

定理7 一个n阶图G和它的补图有相同的频序列。

证明：设图G的任一顶点v的度数为k,则该顶点在补图中的度数为n-1-k。因此：在G中有b个度数为k的顶点，则在补图中就有b个度数为n-1-k个顶点。

作业 P29—P30 8, 9, 10, 11

9、证明：若k正则偶图具有二分类V= V1∪V2，则 | V1| = |V2|。
- 证明：由于G为k正则偶图，所以，k |V1| =m = k|V2| >> |V1|= |V2|。
12、证明：若δ≥2，则G包含圈。

子图与图运算

子图的相关概念

子图
- 边导出子图
- 点导出子图
生成子图 定义3 如果图G的一个子图包含G的所有顶点，称
该子图为G的一个生成子图。

定理1 简单图G=(n, m) 的所有生成子图个数为2^m.

图运算

图的删点、删边运算
- 删点在G中删去v中的顶点和G中与之关联的所有边的操作，称为删点运算
- 删边
- 注：删点要删关联的边，删边不删关联的点！
图的并运算 G1∪G2G1 \cup G2G1∪G2
- 点和边均取交集
- 如果G1,G2不相交(没有公共顶点)，称它们的并为直接并，可以记为：G1+G2G1 + G2G1+G2
图的交运算
- 点和边均取交集
图的差运算
- 设G1,G2是两个图，G1与G2的差是指从G1中删去G2中的边得到的新图。记为G1-G2.
图的对称差运算(或环和运算)
- 设G1,G2是两个图，G1与G2的对称差定义为：
图的联运算
- 设G1,G2是两个不相交的图，作G1+G2，并且将G1中每个顶点和G2中的每个顶点连接，这样得到的新图称为G1与G2的联图。记为：
图的积图
图的合成图
“超立方体”
- n立方体的构造：
  - n方体Q n的顶点可用一个长度为n的二进制码来表示。Q n的顶点数目正好等于2n个。
  - 由n-1方体Q n-1构造Q n的方法是：将Q n-1拷贝一个。将原Q n-1每个顶点的码前再添加一个零，将拷贝得来的n-1方体每个顶点的码前面再添加一个1。然后在两个n-1方体之间连线：当且仅当两个顶点码只有一位对应位数字不同时，该两点连线。如此得到的图即为n方体

路与连通性

路与圈的相关概念

图中的途径
- G 的一条途径（或通道或通路）是指一个有限非空序列：
  w= v0 e1 v1 e2 v2…ek vk，它的项交替地为顶点和边，使得ei的端点是vi-1和vi.(1≤i≤k).
- 途径中边数称为途径的长度；v0,vk分别称为途径的起点与终点，其余顶点称为途径的内部点。
图中的迹 边不重复的途径称为图的一条迹。
图中的路 顶点不重复的途径称为图的一条路。
- 1、路是途径，也是迹，迹是途径；
- 2、起点与终点重合的途径、迹、路分别称为图的闭途径、闭迹与圈。闭迹也称为回路。长度为k的圈称为k圈，k为奇数时称为奇圈，k为偶数时称为偶圈。#

连通性相关概念

两顶点的距离
- 图中顶点u与v的距离：u与v间最短路的长度称为u与v间距离。记为
  d (u, v)，如果u与v间不存在路，定义d (u, v)=∞.
两顶点的连通性 图G中点u与v说是连通的，如果u与v间存在途径。否则称u与v不连通。容易知道：点的连通关系是等价关系。
连通图与连通分支
- (1) 如果图G中任意两点是连通的，称G是连通图，否则，称G是非连通图。
- (2)非连通图中每一个极大连通部分，称为G的连通分支。G的连通分支的个数，称为G的分支数，记为ω(G)\omega(G)ω(G).
图的直径
- 连通图G的直径定义为：
- 如果G不连通，图G的直径定义为无穷大

连通性性质

定理1：若图G不连通，则其补图连通。

偶图的判定定理

定理2 一个图是偶图当且当它不包含奇圈。

证明：
- 必要性：一来一回
- 充分性:
  - 在G中任意选取点u, 定义V的分类如下：
  - X = {x | d (u, x) 是偶数，x ∈V (G)}
  - Y = {y | d (u, y) 是奇数，y ∈V (G)}
  - 下面证明：对X中任意两点v与w , v与w不邻接即可！
  - 注：P−1QP^{-1}QP−1Q为偶，如果vw邻接，则P−1QuvP^{-1}QuvP−1Quv为奇圈

作业 P29—P30 13, 14, 20, 22

13、证明：若G是简单图且δ≥2，则G包含长至少是δ+1的圈。
14、G的围长是指G中最短圈的长；若G没有圈，则定义G的围长为无穷大。证明：
- （1）围长为4的k的正则图至少有2k个顶点，且恰有2k个顶点的这样的图（在同构意义下）只有一个。
- （2）围长为5的k正则图至少有k2+1个顶点

分析： k正则图 \delta = k = \Delta,2m=kn
围长：用邻点集合来分析

20、证明：若G的直径大于3，则G的补图的直径小于3。

考虑G中任意两点u,v
- u,v 相邻
- u,v 不相邻
- 若在V(G)中任意顶点至少和u,v之一相连，>>G的直径大于3，矛盾
- 所以存在一点w,使得uw,wv∉\notin∈/E(G)

22．证明：若G是至少有三个点的简单连通图但不是完全图，则G有三个顶点u, v和w，使得 uv, vw∈E，而uw∉\notin∈/E。

由于G是非完全连通图，所以在G中必然存在不邻接的两点

最短路及其算法

最短路应用

状态转换问题(最少的状态转换次数)
- 例2 某两人有一只8升的酒壶装满了酒，还有两只空壶，分别为5升和3升。求最少的操作次数能均分酒。
- 例3 在一河岸有狼，羊和卷心菜。摆渡人要将它们渡过河去，由于船太小，每次只能载一样东西。由于狼羊，羊卷心菜不能单独相处。问摆渡人至少要多少次才能将其渡过河？
某公司在六个城市C1,C2,C3,C4,C5,C6中有分公司，从Ci到Cj的直接航程票价记在下述矩阵的(i, j)位置上，∞表示没有直接航程。制作一张任意两城市间的最便宜的路线表。

作业 P29—P30 16

1.16 a到其他所有所有的距离

最短路算法求解时,终止条件变为所有顶点被遍历到

图的代数表示及其特征

图的邻接矩阵

定义1 设G为n阶图，V={v1, v2, …, vn}, 邻接矩阵 A(G)=(aij),其中：
邻接矩阵的性质
- (1)非负性与对称性。
- (2) 同一图的不同形式的邻接矩阵是相似矩阵。
- (3) 如果G为简单图，则A(G)为布尔矩阵;行和(列和)等于对应顶点的度数；矩阵元素总和为图的总度数，也就是G的边数的2倍。
- G连通的充分必要条件是：A(G)不能与如下矩阵相似：
  - 证明：
    - 必要性：vi (1≤i≤k)与vj (k+1≤i≤n)不邻接
    - 充分性：设G1与G2是G的两个不连通的部分，并且设
      V(G1)={v1,v2,…,vk}, V(G2)={vk+1,vk+2,…,vn}, 如果在写G的邻接矩阵时，先排V(G1)中点，再排V(G2)中点，则G的邻接矩阵形式必为：
  - 这个性质说明：非连通图的邻接矩阵一定能够写成准
    对角矩阵形式。

定理1 设，则aij(k)a_{ij}^{(k)}aij(k)表示顶点vi到顶点vj的途径长度为k的途径条数。

证明：对k作数学归纳
- 设vm是vi到vj的途径中点，且该点和vj邻接。则vi到vj的经过vm且长度为k的途径数目应该为：
- vi到vj的长度为k的途径数目为：
推论: (1)A2A^2A2的元素aii(2)aii^{(2)}aii(2)是vi的度数，A3A^3A3的元素aii(3)aii^{(3)}aii(3)是含vi的三角形个数的2倍。

图的关联矩阵

定义2 若G是(n, m) 图。定义G的关联矩阵：
关联矩阵的性质
- (1) 关联矩阵的元素为0，1或2；
- (2) 关联矩阵的每列和为2；每行的和为对应顶点度数.

极图

邻接谱、邻接代数与图空间

图的邻接谱
- 定义1：图的邻接矩阵A(G)的特征值及其重数，称为G的邻接谱。
- Kn的邻接谱为：
- 定义2 若两个非同构的n阶图具有相同的谱，则称它们是同谱图。
邻接谱的两个性质
- 定理1 设单图A(G)的谱为：则
  - 证明：
- 定理2 设λ是单图G = (n, m)的任意特征值，则：
图的邻接代数
- 定义3：设A是无环图G的邻接矩阵，则：对于矩阵的加法和数与矩阵的乘法来说作成数域C上的向量空间，称该空间为图G的邻接代数。
定理3：G为n阶连通无环图，则：
图空间

托兰定理

l 部图的概念与特征
- 定义4 若简单图G的点集V有一个划分：且所有的Vi非空，Vi内的点均不邻接，称G是一个l 部图。
定理5 n阶l部图G有最多边数的充要条件是G ≌ Tl,nT_{l,n}Tl,n。
度弱设G和H是两个n阶图，称G度弱于H，如果存在双射μ：V(G)→V(H),使得：

定理6 若n阶简单图G不包含Kl+1K_{l+1}Kl+1，则G度弱于某个完全 l 部图 H，且若G具有与 H 相同的度序列，则:

定理7（Turán）若G是简单图，并且不包含 Kl+1K_{l+1}Kl+1,则：m(G)≤m(Tl,n)m(G) \leq m(T_{l,n})m(G)≤m(Tl,n)

仅当

不含Kl+1K_{l+1}Kl+1的极值图是完全l几乎等部图。

不含子图H(Kl+1K_{l+1}Kl+1)最多边数：m(n,Kl+1)=(l−1)(n2−r2)/(2l)+C(r,2)m(n,K_{l+1}) = (l-1)(n^2-r^2)/(2l)+C(r,2)m(n,Kl+1)=(l−1)(n2−r2)/(2l)+C(r,2)

托兰定理应用：工兵排雷问题

连通偶图的2部划分是唯一的

第二章树

树的概念与性质

树的概念
定义1 不含圈的图称为无圈图，树是连通的无圈图。
定义2 称无圈图G为森林。
注: (1)树与森林都是单图;
(2) 树与森林都是偶图。

定理1 每棵非平凡树至少有两片树叶。

证明设P=v1v2…vk是非平凡树T中一条最长路，则v1与vk在T中的邻接点只能有一个，否则，要么推出P不是最长路，要么推出T中存在圈，这都是矛盾！即说明v1与v2是树叶。

定理2 图G是树当且仅当G中任意两点都被唯一的路连接。

证明：
- “必要性” 若不然，设P1与P2是连接u与v的两条不同的路。则由这两条路的全部或部分将构成一个圈，这与G是树相矛盾。
- “充分性” 首先，因G的任意两点均由唯一路相连，所以G是连通的。其次，若G中存在圈，则在圈中任取点u与v，可得到连接u与v的两条不同的路，与条件矛盾。

定理3 设T是(n, m)树，则：m=n−1m = n - 1m=n−1

证明：对n作数学归纳。
由定理1 T中至少有两片树叶，设u是T中树叶，考虑
T1=T-u,则T1为k阶树，于是m(T1)=k-1, 得m(T)=k。

推论1 具有k个分支的森林有n-k条边。

定理4 每个n阶连通图的边数至少为n-1.

证明：
- 如果n阶连通图没有一度顶点，那么由握手定理有：m(G)=12∑v∈V(G)d(v)≥nm(G) = {1 \over 2}\sum\limits_{v \in V(G)}^{} {d(v)} \ge nm(G)=21v∈V(G)∑d(v)≥n
- 如果G有一度顶点。对顶点数作数学归纳。
  - n=1
  - n=k
  - n=k+1 设u是G的一度顶点,G-u为具有k个顶点的连通图。
    - 若G-u有一度顶点，则由归纳假设，其边数至少k-1,于是G的边数至少有k条；
    - 若G-u没有一度顶点，则由握手定理：m(G)=12∑v∈V(G)d(v)≥nm(G) = {1 \over 2}\sum\limits_{v \in V(G)}^{} {d(v)} \ge nm(G)=21v∈V(G)∑d(v)≥n
    - 所以G至少有k+1条边。

定理5 任意树T的两个不邻接顶点之间添加一条边后，可以得到唯一圈。

证明：路的唯一到圈的唯一
例8 设G是树且Δ≧k,则G至少有k个一度顶点。
证明：反证：握手定理+树的性质
例9设G是森林且恰有2k个奇数顶点，则在G中有k条边不重合的路P1, P2 ,…, Pk,使得：E(G)=E(P1)∪E(P2)∪⋯∪E(Pk)E(G) = E({P_1}) \cup E({P_2}) \cup \cdots \cup E({P_k})E(G)=E(P1)∪E(P2)∪⋯∪E(Pk)
证明：对k作数学归纳。
- 当k=1时，G只有两个奇数度顶点，此时，容易证明，G是一条路；
- 设当k=t时，结论成立。令k=t+1
- 在G中一个分支中取两个一度顶点u与v，令P是连接该两个顶点的唯一路，则G-P是有2t个奇数顶点的森林，由归纳假设，它可以分解为t条边不重合的路之并，所以G可以分解为t+1条边不重合的路之并。

定理6 设S=｛d1,d2,…,dn｝是n个正整数序列，它们满足：d1≧d2≧…≧dn ,∑di=2(n-1).则存在一颗树T，其度序列为S。

证明：对n作数学归纳。
- 当n=1和2时，结论显然。
- 假设对n=k时结论成立。设n=k+1
- 首先,序列中至少一个数为1，否则，序列和大于2k，与条件相矛盾！
- 所以，dk+1=1.我们从序列中删掉d1和dk+1,增加数
  d* =d1-1放在它应该在的位置。得到序列S1.该序列含k个数，序列和为2(k-1),由归纳假设，存在树T1，它的度序列为S1.
- 现在，增加结点v，把它和T1中点d*相连得到树T。树T为所求。

树的中心与形心

(1)图的顶点的离心率e(v)=max⁡{d(u,v)∣u∈V(G)}e(v) = \max \left\{ {d(u,v)\left| {u \in V(G)} \right.} \right\}e(v)=max{d(u,v)∣u∈V(G)}
(2)图的半径r(G)=min⁡{e(v)∣v∈V(G)}r(G) = \min \left\{ {e(v)\left| {v \in V(G)} \right.} \right\}r(G)=min{e(v)∣v∈V(G)}
(3)图的直径：最大离心率。
(4)图的中心点：离心率等于半径的点。
(5)图的中心：中心点的集合。

定理7 每棵树的中心由一个点或两个相邻点组成。

证明：对树T的阶数n作归纳证明。
- 当n=1或2时，结论显然成立。
- 设对n<k(k≧3)的树结论成立。设T是k阶树。
- 容易知道：删掉T的所有叶，得到的树T1的每个点的离心率比它们在T中离心率减少1。又因T的叶不能是中心点，所以T的中心点在T1中。这样，若点u的离心率在T中最小，则在T1中依然最小，即说明T的中心点是T1的中心点，反之亦然。
- 因为T1的阶数<k,所以，由归纳假设，T1的中心为一个点或两个相邻点组成，即证明T的中心由一个点或两个相邻点组成
树的形心概念与性质
- 设u是树T的任意一个顶点，树T在顶点u的分支是指包含u作为一个叶点的极大子树，其分支数为顶点u的度数；树T在u点的分支中边的最大数目称为点u的权；树T中权值最小的点称为它的一个形心点。全体形心点的集合称为树T的形心。

定理8 每一棵树有一个由一个点或两个邻接的点组成的形心。

作业 P43 习题2 ： 1，2，3，4，5，6

2.1 证明：非平凡树的最长路的起点和终点均是 1 度的。
- 反证
2.2 证明：每棵恰有两个1 度顶点的树均是路。
- 反证: 握手定理+ 树的性质
2.3 若G 是树且最大度 >= k ，则G 至少有k个 1 度顶点。
- 反证：握手定定理+树的性质
2.4 见例题9
2.5 证明：正整数序列1 2 ( , , , ) k d d  d 是一棵树的度序列当且仅当度数和为2(n-1)
- 证明：
  - 必要性： m=n-1
  - 充分性：对n作数学归纳 (见定理6)
2.6 设T 是有k 1个顶点的任意一棵树。证明：若G 是简单图且δ≥k\delta\geq kδ≥k，则G 有一个
子图同构于T 。
- 证明：对k进行归纳。
- 当k=1时，结论显然成立
- k=n 显然成立

生成树

生成树的概念与性质

定义1 图G的一个生成子图T如果是树，称它为G的一棵生成树；若T为森林，称它为G的一个生成森林。
生成树的性质

定理1 每个连通图至少包含一棵生成树。

证明：如果连通图G是树，则其本身是一棵生成树；若连通图G中有圈C，则去掉C中一条边后得到的图仍然是连通的，这样不断去掉G中圈，最后得到一个G的无圈连通子图T，它为G的一棵生成树
推论若G是(n, m)连通图，则m≧n-1

生成树的计数

凯莱递推计数法

定义2 图G的边e称为被收缩，是指删掉e后，把e的两个端点重合，如此得到的图记为G.e
用τ(G)表示G的生成树棵数。

定理2 (Cayley) 设e是G的一条边，则有：τ(G)=τ(G−e)+τ(Ge)\tau (G) = \tau (G - e) + \tau (Ge)τ(G)=τ(G−e)+τ(Ge)

证明：对于G的一条边e来说，G的生成树中包含边e的棵数为τ(G.e )，而不包含e的棵数为τ (G-e).
例题

关联矩阵计数法

定义3 ：n×m矩阵的一个阶数为min｛n, m｝的子方阵，称为它的一个主子阵；主子阵的行列式称为主子行列式。
显然，当n<m时，n×m矩阵CmnC_m^nCmn个主子阵。

定理3 设Am是连通图G的基本关联矩阵的主子阵，则Am非奇异的充分必要条件是相应于Am的列的那些边构成G的一棵生成树。

该定理给出了求连通图G的所有生成树的方法：
- (1) 写出G的关联矩阵，进一步写出基本关联矩阵(选一个点，去掉该点对应的行)，记住参考点；（因为m=n-1）
- (2) 找出基本关联矩阵的非奇异主子阵，对每个这样的主子阵，画出相应的生成树。

矩阵树定理

定理4 (矩阵树定理) 设G是顶点集合为V(G)=｛v1,v2,…,vn｝,的图，设A=(aij)是G的邻接矩阵，C=(cij)是n阶方阵，其中：

则G的生成树棵数为C的任意一个(代数)余子式的值。

定理中的矩阵C又称为图的拉普拉斯矩阵，又可定义为：C=D(G)−A(G)C = D(G) - A(G)C=D(G)−A(G)其中，D(G)是图的度对角矩阵，即主对角元为对应顶点度数，其余元素为0。A(G)是图的邻接矩阵。
例4 证明τ(Kn)=nn-2(教材上定理7）

回路系统简介

定义4 连枝树枝 设T是连通图G的一棵生成树，把属于G但不属于T的边称为G关于T的连枝，T中的边称为G关于T的树枝。
定义5 基本回路 设T是连通图G的一棵生成树，由G的对应于T一条连枝与T中树枝构成的唯一圈C，称为G关于T的一个基本圈或基本回路。若G是(n, m)连通图，把G对应于T的m-n+1个基本回路称为G对应于T的基本回路组。记为Cf…
基本回路的性质:

定理4 设T是连通图G=(n, m) 的一棵生成树,C1, C2,…,Cm-n+1是G对应于T的基本回路组。定义：1.Gi=Gi , 0.Gi=Φ,Gi是G的回路。则G的回路组作成的集合对于该乘法和图的对称差运算来说作成数域F=｛0,1｝上的m-n+1维向量空间。

说明: 连通图G的所有回路作成子图空间的一个子空间，该空间称为回路空间或回路系统。
例5 求下图G的回路空间的一个基底和它的全部元素。

P43 习题2 ： 12, 14, 15

2.12 求K3,3的生成树数量
2.14 证
2.15

分析：

选边

破圈法，不同的破圈方式

最小生成树

克鲁斯克尔算法

思想：从G中的最小边开始，进行避圈式扩张。
定理1 由克鲁斯克尔算法得到的任何生成树一定是最小生成树。(证明略)

管梅谷的破圈法

破圈法求最小生成树的求解过程是：从赋权图G的任意圈开始，去掉该圈中权值最大的一条边，称为破圈。不断破圈，直到G中没有圈为止，最后剩下的G的子图为G的最小生成树。

Prim算法

对于连通赋权图G的任意一个顶点u，选择与点u关联的且权值最小的边作为最小生成树的第一条边e1;
在接下来的边e2,e3,…,en-1 ,在与一条已经选取的边只有一个公共端点的的所有边中，选取权值最小的边。
反证法可以证明该算法。即证明：由Prim算法得到的生成树是最小生成树。(证明略)

根树简介

定义2：一棵树T，如果每条边都有一个方向，称这种树为有向树。对于T的顶点v来说，以点v为终点的边数称为点v的入度，以点v为起点的边数称为点v的出度。入度与出度之和称为点v的度。
定义3 根树：一棵非平凡的有向树T，如果恰有一个顶点的入度为0，而其余所有顶点的入度为1，这样的的有向树称为根树。其中入度为0的点称为树根，出度为0的点称为树叶，入度为1，出度大于1的点称为内点。又将内点和树根统称为分支点。
定义4：对于根树T，顶点v到树根的距离称为点v的层数；所有顶点中的层数的最大者称为根树T的树高。
定义5：对于根树T，若规定了每层顶点的访问次序，这样的根树称为有序树。
注：一般次序为从左至右。有时也用边的次序代替顶点次序。
定义6：对于根树T，由点v及其v的后代导出的子图，称为根树的子根树。
定义7：对于根树T，若每个分支点至多m个儿子，称该根树为m元根树；若每个分支点恰有m个儿子，称它为完全m元树。

定理2 在完全m元树T中，若树叶数为t , 分支点数为i , 则：(m−1)i=t−1(m - 1)i = t - 1(m−1)i=t−1

证明：一方面，由树的性质得：m(T)=(i+t)−1⋯(1)m(T) = (i + t) - 1 \cdots (1)m(T)=(i+t)−1⋯(1)
另一方面，由握手定理得：
2m(T)=t+m+(i−1)(m+1)⋯(2)2m(T) = t + m + (i - 1)(m + 1) \cdots (2)2m(T)=t+m+(i−1)(m+1)⋯(2)
例5 一台计算机，它有一条加法指令，可以计算3个数的和。如果要求9个数的和，问至少执行多少次加法指令？
对于一棵有序树，常要转化为二元树。方法是：
- (1) 从根开始，保留每个父亲同其最左边儿子的连线，撤销与别的儿子的连线；
- (2) 兄弟间用从左至右的有向边连接；
- (3) 按如下方法确定二元树中结点的左右儿子：直接位于给定结点下面的儿子，作为左儿子，对于同一水平线上与给定结点右邻的结点，作为右儿子，依此类推。
二元树的遍历问题
最优二元树
定义8 设T是一棵二元树，若对所有t片树叶赋权值wi(1≦i≦t),且权值为wi的树叶层数为L(wi),称：
W(T)=∑i=1twiL(wi)W(T) = \sum\limits_{i = 1}^t {{w_i}} L({w_i})W(T)=i=1∑twiL(wi)
为该赋权二元树的权。而在所有赋权为wi的二元树中
W(T)最小的二元树称为最优二元树。
哈夫曼算法：
- (1) 初始：令S=｛w1,w2,…,wt｝;
- (2) 从S中取出两个权值最小者wi与wj ,画结点vi ,带权wi,画结点vj，带权wj，画vi与vj的父亲v，连接vi与v,连接vj与v,令v带权wi + wj ;
- (3) 令S = (S-｛wi ,wj｝)∪｛wi+wj｝;
- (4) 判断S是否只含一个元素，若是，停止，否则转2).

P43 习题2 ： 16, 17, 18

2.16
2.17
2.18（未弄懂）

第三章图的连通度

割边，割点和块

割边及其性质

定义1 边e为图G的一条割边，如果ω(G−e)>ω(G)\omega (G - e) > \omega (G)ω(G−e)>ω(G)
- 注：割边又称为图的“桥”。

定理1 边 e 是图G的割边当且仅当 e 不在G的任何圈中。

证明：
- 必要性：
- 充分性：

推论1 e为连通图G的一条边，如果e含于G的某圈中，则G-e连通。

例1 求证: (1) 若G的每个顶点的度数均为偶数，则G没有割边; (2) 若G为k正则二部图(k≧2)，则G无割边。
- 证明：
- （1）

割点及其性质

定义2 在G中，如果E(G)可以划分为两个非空子集E1与E2,使G[E1]和G[E2]以点v为公共顶点，称v为G的一个割点。
注：环的点算割点

定理2 G无环且非平凡，则v是G的割点，当且仅当ω(G−v)>ω(G)\omega (G - v) > \omega (G)ω(G−v)>ω(G)

证明：

定理3 v 是树T的顶点，则v是割点，当且仅当v是树的分支点。

证明：
例2 求证：无环非平凡连通图至少有两个非割点
例3 求证：恰有两个非割点的连通单图是一条路。
- 一个单图的任意生成树为路，则该图为圈或路
例4 求证：若v是单图G的割点，则它不是G的补图的割点。

定理4 设v是无环连通图G的一个顶点，则v是G的割点，当且仅当V(G-v)可以划分为两个非空子集V1与V2,使得对任意x ∈V1, y ∈V2, 点v在每一条x y路上。

块及其性质

定义3 没有割点的连通图称为是一个块图，简称块；G的一个子图B称为是G的一个块，如果(1), 它本身是块；(2), 若没有真包含B的G的块存在。

定理5 若|V(G)|≧3,则G是块，当且仅当G无环且任意两顶点位于同一圈上。

证明：
- 必要性: G不能有割点，显然无环
  - 证任意u,v在同一圈
    - 对d(u,v)做数学归纳
- 充分性：反证

定理6 点v是图G的割点当且仅当v至少属于G的两个不同的块。

证明：
块割点树 为了直观反映图的块和割点之间的联系，引进所谓的块割点树。
设G是非平凡连通图。B1, B2 ,…, Bk是G的全部块，而v1,v2,…, vt是G的全部割点。构作G的块割点树 b c (G):它的顶点是G的块和割点，连线只在块割点之间进行，一个块和一个割点连线，当且仅当该割点是该块的一个顶点。

P65—66 习题3 ： 1, 2, 3,5,7,8

3.1 证明：e是连通图G的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意u∈V_1及v∈V_2, G中的路（u，v）必含e.
3.2
3.3 设G是阶大于2的连通图，证明下列命题等价：
- （1） G是块
- （2） G无环且任意一个点和任意一条边都位于同一个圈上；
- （3） G无环且任意三个不同点都位于同一条路上。

证明：
(1)>(2) : 边上插入点
(2)>(3): （存疑：如何保证任意性）G无环，且任意一点和任意一条边都位于同一个圈上，任取G的点u，边e，若u不在e上，则三个不同点位于同一个圈，即位于同一条路，如u在e上，由定理e的两点在同一个圈上，在e边插入一个点v，使得e成为2条边，由此得到新图G_1，显然G_1的是阶数大于2的块，则两条边的三个不同点在同一条路上。
(3)>(1): G连通，若G不是块，则G中存在着割点u，划分为不同的子集块V_1, V_2, V_1, V_2无环，点u在每一条(x,y)的路上，由于x,y的任意性，则三个不同点不能位于同一条路上，则与已知矛盾，G是块。

3.5 证明:恰有两个非割点的连通图是路

连通 > 存在生成树
恰有两个割点 >> 生成树只有两个非割点(树叶) >> 生成树为路
任意生成树为路 >> 圈或路 >> 存在割点只能是路

3.7 (同例题4)求证：若v是单图G的割点，则它不是G的补图的割点。
3.8 证明：块的个数 ω+sum(b(v)−1)\omega + sum (b(v)-1)ω+sum(b(v)−1) b(v)为含v的块的个数 (未解决)

分析：

先证：ω=1\omega = 1ω=1的时候：数学归纳？
非割点只属于一个块

连通度

连通度的概念与性质

点连通度与边连通度的概念

定义1 给定连通图G，设 V′⊆V(G)V' \subseteq V(G)V′⊆V(G)，若G -V’ 不连通，称V’为G的一个点割集，含有k个顶点的点割集称为k顶点割。G中点数最少的顶点割称为最小顶点割。
定义2 在G中，若存在顶点割，称G的最小顶点割的顶点数称为G的点连通度；否则称n-1为其点连通度。G的点连通度记为k(G), 简记为k。若G不连通，k(G)=0。
定义3 在G中，最小边割集所含边数称为G的边连通度。边连通度记为λ(G) 。若G不连通或G是平凡图，则定义λ(G) =0
定义4 在G中，若k (G)≧ k, 称G是k连通的；若λ(G)≧k，称G是k边连通的。

连通度的性质

定理1 (惠特尼1932) 对任意图G，有：k(G)≤λ(G)≤δ(G)k(G) \le \lambda (G) \le \delta (G)k(G)≤λ(G)≤δ(G)

证明：

定理2 设G是(n, m)连通图，则：k(G)≤⌊2mn⌋k(G) \le \left\lfloor {{{2m} \over n}} \right\rfloor k(G)≤⌊n2m⌋

证明：握手定理 + 惠特尼定理

哈拉里图:涉及可靠性通信网络构建

1962年，数学家哈拉里构造了连通度是k,边数为$m = \left\lfloor {{{nk} \over 2}} \right\rfloor $
的图Hk, n ,称为哈拉里图。
哈拉里构图
- H2r,n
  - E(H)={ij∣∣i−j∣≤r(n)(取模n的加法).}E(H) = \left\{ {ij\left| {\left| {i - j} \right| \le r(n)} \right(取模n的加法).} \right\}E(H)={ij∣∣i−j∣≤r(n)(取模n的加法).}
- H2r+1,n (n为偶数)
  - 先作H2r,n, 然后对1≦i≦n/2,i与i+n/2连线。
- H2r+1,n (n为奇数)
  - 先作H2r,n, 然后对1≦i≦(n-1)/2,i与i+(n+1)/2连线。同时，0分别与(n-1)/2和(n+1)/2连线。

定理3 设G是(n, m)单图，若$\delta (G) \ge \left\lfloor {{{\rm{n}} \over {\rm{2}}}} \right\rfloor $，则G连通。

证明：

定理4 设G是(n, m)单图，若对任意正整数k ,有：δ(G)≥n+k−22\delta (G) \ge {{n + k - 2} \over 2}δ(G)≥2n+k−2则G是k连通的。

证明：证明：任意删去k-1个顶点，记所得之图为H，则：δ(H)≥δ(G)−(k−1)≥n+k−22−k+1=n−k2\delta (H) \ge \delta (G) - (k - 1) \ge {{n + k - 2} \over 2} - k + 1 = {{n - k} \over 2}δ(H)≥δ(G)−(k−1)≥2n+k−2−k+1=2n−k
由于δ(H)是整数，故：δ(H)≥⌈n−k2⌉=⌊n−k+12⌋\delta (H) \ge \left\lceil {{{n - k} \over 2}} \right\rceil = \left\lfloor {{{n - k + 1} \over 2}} \right\rfloor δ(H)≥⌈2n−k⌉=⌊2n−k+1⌋

定理5 设G是n阶单图，若δ(G)≥⌊n2⌋\delta (G) \ge \left\lfloor {{n \over 2}} \right\rfloor δ(G)≥⌊2n⌋则有：λ(G)=δ(G)\lambda (G) = \delta (G)λ(G)=δ(G)

证明：

P66—67 习题3 ： 1 2, 13, 14, 20

3.1
3.2
3.13 举例
3.14
3.20 证： n阶简单图 δ≥n−1\delta \geq n-1δ≥n−1 则k=δk = \deltak=δ

描述连通性的其它参数简介(内容拓展)

敏格尔定理

定义1 设u与v是图G的两个不同顶点，S表示G的一个顶点子集或边子集，如果u与v不在G-S的同一分支上，称S分离u和v。

定理1 (敏格尔1902—1985) (1) 设x与y是图G中的两个不相邻点，则G中分离点x与y的最少点数等于独立的(x, y)路的最大数目；

定理2 (惠特尼1932) 一个非平凡的图G是k (k≧2)连通的，当且仅当G的任意两个顶点u与v间，至少存在k条内点不交的(u ,v)路。

例1 设G是k连通图，S是由G中任意k个顶点构成的集合。若图H是由G通过添加一个新点w以及连接w到S中所有顶点得到的新图，求证：H是k连通的。

定理3 (惠特尼1932) 一个非平凡的图G是k (k≧2)边连通的，当且仅当G的任意两个顶点间至少存在k条边不重的(u ,v)路。

证明：
- 必要性：考虑任意两点 u,v
  - 讨论相邻与不相邻
- 充分性：
例1 设G是k连通图，S是由G中任意k个顶点构成的集合。若图H是由G通过添加一个新点w以及连接w到S中所有顶点得到的新图，求证：H是k连通的。

推论对于一个阶至少为3的无环图G，下面三个命题等价。

(1) G是2连通的；
(2) G中任意两点位于同一个圈上；
(3) G无孤立点，且任意两条边在同一个圈上。
证明：

(1)→(2)
G是2连通的,则G的任意两个顶点间存在两条内点不交路P1与P2,显然这两条路构成包含该两个顶点的圈。
(2)→(3)
G无孤立点显然。设e1与e2是G的任意两条边，在e1与e2上分别添加两点u与v得图H，则H是2连通的，由(1)→(2)，H的任意两个顶点在同一个圈上，即u与v在同一个圈上，也即e1与e2在同一个圈上。
(3)→(1)
设u与v是无环图G的任意两个不相邻顶点，由于G无孤立点，所以可设e1,e2分别与u, v相关联。由(3),e1,e2在同一个圈上，所以u与v在同一个圈上，因此分离u与v至少要去掉两个顶点，即证明G是2连通的。

第一次上交作业

习题1 ： 4，5, 11，12, 17，18.
习题2 ： 1，9, 16.
习题3 ： 1，3, 7, 12，13.

第四章欧拉图与Hamilton图

欧拉图及其性质

基本概念
- 定义一（欧拉图与欧拉回路） 对于连通图G，如果G中存在经过每条边的闭迹，则称G为欧拉图，简称G为E图。欧拉闭迹又称为欧拉环游，或欧拉回路。

欧拉图的性质

定理一下列陈述对于非平凡连通图G是等价的

G是欧拉图
G的顶点度数为偶数
G的边集合能划分为圈

定理一证明:
- 1 >> 2: 一进一出
- 2 >> 2: 减圈法
- 3 >> 1: 拼圈法

推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。

推论2 连通非欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。

例题：

例题1 证明： 欧拉图GGG与欧拉图HHH的乘积G×HG \times HG×H仍然是欧拉图.
- 先证明d((u,v)) = d(u) + d(v) [邻点(u,w)(u,w)(u,w)，www有d(u)d(u)d(u)种，邻点u(x,v)u(x,v)u(x,v),xxx有d(v)d(v)d(v)种]
- 证明G×HG\times HG×H是连通的 (u1,v1)与(u2,v2) 连通
  （u1,v1）>>(u1,v2)>>(u2,v2)（u1,v1）>> (u1,v2) >> (u2,v2)（u1,v1）>>(u1,v2)>>(u2,v2)
一笔画问题：欧拉迹存在问题
几笔画问题：添加几笔成为欧拉图

其他性质：

欧拉图不存在割边
欧拉图举例
- 完全图KnK_nKn，n为奇时为欧拉图
- n立方体QnQ_nQn,n为偶数为欧拉图
- 完全二部图Ka,bK_{a,b}Ka,b, a,ba,ba,b 均为偶数时为欧拉图
例题2若G是非平凡的欧拉图，则G的每个块也是欧拉图。
- 证明：对于任一块，欧拉回路跨越两个块，必然经过割点，按割点分割的欧拉回路，是每个块的欧拉回路。

例题3 **（未弄懂）

设G是非平凡的欧拉图，且v∈V(G)。证明：G的每条以v为起点的迹都能扩展成G的欧拉回路** 当且仅当 G‒v是森林。
- 必要性：非B >> 非A:
- 充分性：

Fleury(夫勒里)算法 (求一条具体欧拉环游的方法)

基本思想：尽可能避割边行走
算法：
- 任意选择一个顶点v0v_0v0,置w0=v0w_0 = v_0w0=v0
- 假设迹 wi=v0e1v1...eiviw_i = v_0e_1v_1...e_iv_iwi=v0e1v1...eivi 已经选定，按一下要求从剩余边集合种选取下一条边 ei+1e_i+1ei+1:
  - ei+1e_i+1ei+1 与 viv_ivi 相关联
  - 除非没有的边可选择，否则 ei+1e_i+1ei+1 不能是 Gi=G−e1,...,eiG_i = G - {e_1,...,e_i}Gi=G−e1,...,ei 的割边
- 迭代第二步，直至无边可选
例题4 证明 若 GGG 有 2k>02k>02k>0个奇数顶点，则存在k条边不重的迹Q1,Q2,…,QkQ1,Q2,…,QkQ1,Q2,…,Qk，使得： E(G)=E(Q1)∪E(Q2)∪...∪E(Qk)E(G) = E(Q_1) \cup E(Q_2) \cup ... \cup E(Q_k)E(G)=E(Q1)∪E(Q2)∪...∪E(Qk)
- 证明： (vi,vi+kv_i,v_i+kvi,vi+k间)加边 >> 欧拉图 >> 圈的集合 >> 去边 >> 迹的集合

中国邮路问题

问题：每条街道至少走一次,如何用最少路程，回到邮局。

求最优环游：

欧拉图，最优环游为欧拉回路
对一般图，解法：添加重复边以使得 G 成为欧拉图 G*，并使得添加的重复边的边权之和为最小，再求G* 的欧拉回路：
- 用每条边最多添一次的方法任意添一些重复边使图G成为一个欧拉多重图G′。
- 考查G′的圈，若存在圈C，其中重复边的总权值大于该圈权值的一半，则在圈C上交换重复边和不重复边得到一个新的欧拉多重图。重复这个过程，直到得到一个图G*，使得图G*中每个圈上重复边的总权值不大于该圈权值的一半。
- 用Fleury算法求G*的Euler回路。
定理2（管梅谷） 若W是包含图G的每条边至少一次的闭途径，则W具有最小权值当且仅当下列两个条件被满足：
- (1) G的每条边在W中最多重复一次;
- (2) 对于G的每个圈上的边来说，在W中重复的边的总权值不超过该圈非重复边总权值。
定理2 证明
- 必要性：(奇度点对之间的路上的边改为2重边) >> 欧拉图G1 >> 删去重数>2的边 >> 欧拉图G2 >> 假定不满足（1）（2）可得更优 w。（没看太懂）
- 充分性：略
非欧拉图，求最优环游：
- 奇度点配对
- 奇度间找条路路上添加重复边
- 按照定理2修改修改到最优：
  - 考查G′的圈，若存在圈C，其中重复边的总权值大于该圈权值的一半，则在圈C上交换重复边和不重复边得到一个新的欧拉多重图。重复这个过程，直到得到一个图G*，使得图G*中每个圈上重复边的总权值不大于该圈权值的一半。
- 求 G∗G^*G∗ 的欧拉环游
例题5 求最优欧拉环游
例6 如果一个非负权的边赋权图G中只有两个奇度顶点u与v,设计一个求其最优欧拉环游的算法。
- 算法设计：
  - (1)、在u与v间求出一条最短路P; (最短路算法)
  - (2)、在最短路P上，给每条边添加一条平行边得G的欧拉母图G*;
  - (3)、在G的欧拉母图G* 中用Fleury算法求出一条欧拉环游。
- 证明：重复边的权值和 ≥ 任意路 ≥ 最短路

Hamilton图

哈密尔顿图的概念

定义
- 经过图中每个点的路称为Hamilton路，简称H路。
- 经过图中每个点的圈称为Hamilton圈，简称H圈。
- 存在Hamilton圈的图称为Hamilton图，简称H图。
思考
- Hamilton图举例
  - 正十二面体图
  - n>=3n>=3n>=3的完全图 KnK_nKn
  - n>=2n>=2n>=2,n立方体QnQ_nQn
  - 完全二部图Ka,bK_{a,b}Ka,b当a=b>=2a=b>=2a=b>=2时
- 是否存在一个具有奇数个顶点的连通图既是二部图，又是Hamilton图
  - 不存在，否则二部图种出现了奇圈
- 二部图G是Hamilton图（二部划分为X,Y）须满足 |X|=|Y|(必要条件)
- 例题1 若G1和G2是H图，则G1×G2是H图。

性质与判定

定理1（必要条件）若G是H图，则对于V的每个非空真子集S，均有ω(G−S)≤∣S∣ω(G-S)≤|S|ω(G−S)≤∣S∣ 。

证明：ω(G−S)≤ω(C−S)≤∣S∣ω(G-S)≤ω(C-S)≤|S|ω(G−S)≤ω(C−S)≤∣S∣ 其中CCC为GGG的GGG圈
例题2 **（未看）**彼得森图不是H图，但满足定理中的条件
例题3 证明：若连通图不是2-连通的，则G不是Hamilton图
- 存在割点，ω(G−v)≥2>1=∣v∣ω(G-v)≥2>1=|{v}|ω(G−v)≥2>1=∣v∣ 不满足必要条件
- 推论 Hamilton图一定不存在割点

定理2 若图G包含哈密尔顿路，则对V(G)的每个真子集S，ω(G−S)≤∣S∣+1。ω(G-S) ≤ |S|+1。ω(G−S)≤∣S∣+1。

证明：ω(G−S)≤ω(P−S)≤∣S∣+1。ω(G-S) ≤ ω(P-S) ≤ |S|+1。ω(G−S)≤ω(P−S)≤∣S∣+1。
例题4 若图G是哈密尔顿图且不是圈，则G至少包含2个度数不小于3的顶点。
证明：反证：若只有一个度不小于3的顶点，则该点为割点

定理3（充分条件） (Dirac 1952) 对于n≥3的简单图G，如果G中有：δ(G)≥n/2\delta (G) \geq n/2δ(G)≥n/2 则G是H图

证明：（反证法）
- 极大非H简单图G′G'G′：任意添加边uv都成为H图
- G′G'G′ 的H路P=v1v2...vnP = v_1v_2...v_nP=v1v2...vn
- S={vi∣v1vi+1∈E(G)}S=\{v_i|v1v_{i+1}\in E(G)\}S={vi∣v1vi+1∈E(G)} T={vi∣vnvi∈E(G)}T=\{v_i|v_nv_i\in E(G)\}T={vi∣vnvi∈E(G)}
- S∩T=∅S\cap T = \emptyS∩T=∅ 否则存在Hamilton圈
- $d(v_1)+d(v_n) = |S| +|T| < n 则与则与则与\delta (G) \le n/2$ 矛盾

定理4（充分条件） (Ore 1962) 对于n≥3的简单图G，如果G中的任意两个不相邻顶点u与v，有：d(u)+d(v)≥nd(u)+d(v)\geq nd(u)+d(v)≥n 则G是H图

注：证明与定理3一致，该定理的条件是紧的。

闭图与闭包基本概念

闭图定义 在n阶简单图G中，若对d(u)+d(v)≥n的任何一对点u和v都是相邻的，则称G是闭图。
定理若G1和G2是同一个点集V的两个闭图，则G=G1∩G2G=G1∩G2G=G1∩G2是闭图。
- 证明： dG(u)+dG(v)>=nd_{G}(u)+d_{G}(v)>=ndG(u)+dG(v)>=n 则 dG1(u)+dG1(v)>=nd_{G_1}(u)+d_{G_1}(v)>=ndG1(u)+dG1(v)>=n +dG2(u)+dG2(v)>=nd_{G_2}(u)+d_{G_2}(v)>=ndG2(u)+dG2(v)>=n ，容易知道u,v在G1,G2邻接所以在G中也邻接
闭包定义 若一个与G 有相同点集的闭图 Ĝ，使G⊂G^G \subset ĜG⊂G^，且对异于Ĝ的任何图H，若有G⊂H⊂G^G \subset H \subset ĜG⊂H⊂G^，则H不是闭图，则称Ĝ是G的闭包。（G的闭包是包含G的极小闭图）
- 图G的闭包唯一
- 对于单图G，如果G中有两个不相邻顶点u与v，满足：d(u)+d(v)≥nd(u)+d(v)≥nd(u)+d(v)≥n，那么G是H图当且仅当G + u v是H图。
闭包的构造： 如果G本身是闭图，则其闭包是它本身；如果G不是闭图，则由定义可以通过在度和大于等于n的不相邻顶点对间加边来构造G的闭图。

邦迪——闭包定理（充要条件）图G是H图当且仅当它的闭包是H图。

推论1： 设G是n≧3的单图，若G的闭包是完全图，则G是H图。
推论2： 设G是n≧3的单图。若δ(G)≧n/2,则G是H图 (Dirac定理)。
推论3： 若对于G中任意不相邻顶点u与v，都有d(u)+d(v)≧n,则G是H图.(Ore定理)

定理5(Chvátal——度序列判定法) 设简单图G的度序列是(d1,d2,…,dn), 这里，d1≦d2≦…≦dn,并且n≧3.若对任意的m<n/2,或有 dm>m,或有dn-m ≧ n-m,则G是H图。【可以证明，满足条件的图的闭包是完全图】（否命题：存在m<n/2,有 dm<=m,且dn-m<n-m）

非哈密尔顿图与TSP问题

非Hamilton图特征

定义1 图G称为度极大非H图，如果它的度不弱于其它非H图。
定义2 对于1≦m<n/21≦ m <n/21≦m<n/2, Cm,nC_{m,n}Cm,n图定义为：Cm,n=Km∨(K‾m+Kn−2m)C_{m,n} = K_m \vee (\overline K_m + K_{n-2m})Cm,n=Km∨(Km+Kn−2m)

引理1 对于1≦m <n/2 的图Cm,nC_{m,n}Cm,n是非H图。

证明：取S=KmS = {K_m}S=Km ,w(G−S)=m+1>m=∣S∣w(G-S)=m+1>m=|S|w(G−S)=m+1>m=∣S∣(不符合H图的必要条件)

定理1 (Chvátal,1972) 若G是n≧3的非H单图，则G度弱于某个Cm,nC_{m,n}Cm,n图。

证明：

推论1 n(≥3)阶单图若度优于Cm,nC_{m,n}Cm,n 图族中所有图，则G是H图。

例1(证明题) 设G是度序列为(d1,d2,…,dn)的非平凡单图，且d1≦d2≦…≦dn。证明：若G不存在小于(n+1)/2的正整数m，使得：dm<m且dn-m+1<n-m,则G有H路。
- 证明：(G1=G∪vG1 = G \cup vG1=G∪v) >> 度序列判定G1为H图 >> $ G = G1 - v$ 存在H路
例2(应用题) 一只老鼠吃3∗3∗33*3*33∗3∗3立方体乳酪。其方法是借助于打洞通过所有的27个$111 $的子立方体。如果它从一角上开始，然后依次走向未吃的立方体，问吃完时是否可以到达中心点？
解：H路存在性问题：
- 图建模 >> 偶图划分为13:14
- |X| ！= |Y| (加边（起点-中心点）后)不能存在圈（w(G1−Y)=14>∣Y∣=13w(G1-Y)=14>|Y|=13w(G1−Y)=14>∣Y∣=13） >> 原图不能存在H路

TSP问题（旅行售货员问题）

边交换技术[有权完全图]（求近似最优哈密尔顿圈）

在赋权完全图中取一个初始H圈C=v1v2,…,vnv1C = v1v2,…,vnv1C=v1v2,…,vnv1；
如果存在下图中红色边，且w(vivi+1)+w(vjvj+1)≧w(vivj)+w(vi+1vj+1)w(v_iv_{i+1})+ w(v_jv_{j+1})≧w(v_iv_j)+ w(v_{i+1}v_{j+1})w(vivi+1)+w(vjvj+1)≧w(vivj)+w(vi+1vj+1),则把C修改为：$ C1=v1v2,…,vivj…vi+1vj+1…,vnv1$；
反复修改，直到不能修改为止。最后圈为近似最优哈密尔顿圈。
例3 采用边交换技术求赋权完全图的一个近似最优H圈。

赋权完全图中最优H圈下界估计

(1) 在G中删掉一点v(任意的)得图G1;
(2) 在图G1中求出一棵最小生成树T;
(3) 在v的关联边中选出两条权值最小者e1与e2.
若H是G的最优圈，则：W(H)≥W(T)+W(e1)+W(e2)W(H)\geq W(T)+W(e_1)+W(e_2)W(H)≥W(T)+W(e1)+W(e2)

超Hamilton图与超可迹图

超H图与超可迹图

定义1 若图G是非H图，但对于G中任意点v,都有G-v是H图，则称G是超H图。
- 举例：彼德森图
  - 证明： 1. 证G为非H图 2. 证G-v为H图
定义2 若G中没有H路，但是对G中任意点v，G-v存在H路，则称G是超可迹的。
- 定理2 Thomassen图是超可迹图。
  - 证明： 1. 证明G中不存在H路。
一些研究
- 普鲁默猜想：每个2连通图的平方是H图。
  - 图的平方原图GGG中距离小于等于2的点在G2G^2G2中邻接

定理：每个3正则H图至少有3个生成圈。

E图与H图的关系

线图

定义3 设G是图，G的线图L(G)定义为：V(L(G))=E(G),(e1,e2∈E(L(G)))↔在G中有：e1,e2邻接V(L(G))=E(G),(e_1,e_2\in E(L(G))) \leftrightarrow在G中有：e_1,e_2邻接V(L(G))=E(G),(e1,e2∈E(L(G)))↔在G中有：e1,e2邻接
特别地，定义G的n次迭线图Ln(G) 为：Ln(G)=L(Ln−1(G))L^n(G) = L(L^{n-1}(G))Ln(G)=L(Ln−1(G))
线图的性质
- (1) 线图L(G)顶点数等于G的边数；若e=u v是G的边，则e作为L(G)的顶点度数为：d(e)=d(u)+d(v)−2d(e)=d(u)+d(v)-2d(e)=d(u)+d(v)−2.
- (2) 若G=(n, m), 则线图L(G) 边数为：$m(E(L(G)) = - m + \frac{1}{2}\sum\limits_{v \in V(G)}^{} {{d^2}(v)} $
- (3) 一个图同构于它的线图，当且仅当它是圈。
- (4) 若图G和G1有同构的线图，则除了一个是K3而另一个是K1,3外，G和G1同构。(证明比较复杂)
从线图考察E图与H图
- 定义4 称Sn是图G的n次细分图，是指将G的每条边中都插入n个2度顶点。
  - Ln(G)=L(Sn−1(G)){L_n}(G) = L({S_{n - 1}}(G))Ln(G)=L(Sn−1(G))

定理3 (1)若G是E图，则L(G) 既是E图又是H图。 (2)若G是H图，则L(G)是H图。

定理4 一个图G 是E图的充要条件是L3(G)为H图

定理5（Chartarand）若G 是n个点的非平凡连通图，且不是一条路，则对所有m≥n-3，Lm(G) 是H图。

习题4 ： 1, 2, 3, 7, 8, 9

习题4 ： 1, 3， 4, 7，8， 11， 15.
4.1 一笔画问题：是否存在欧拉迹，即最多只能有两个奇度顶点
4.2 几笔画问题：奇点数除以二便可算出此图需几笔画成
4.3 画图举例 —— Hamilton圈与Euler闭迹：
4.4 设n阶无向简单图G有m条边。证明：若m≥(n-1 2) +2，则G是哈密尔顿图。
- 证明：同第二次作业3
  - 托兰定理
4.7 证明：若G没有奇点，则存在边不重的圈C1, C2,…, Cm，使得，E(G) = E(C1)∪E(C2)∪…∪E(Cm)。
去圈法
4.8 证明：若G有2k＞0个奇点，则存在k条边不重的迹Q1, Q2,…, Qk，使得，E(G) = E(Q1)∪E(Q2)∪…∪E(Qk)。：
加边 >> 欧拉图 >> 圈集合 >> 去边 >> 迹集合
4.9 同例题3
4.11 证明 定理2 若图G包含哈密尔顿路，则对V(G)的每个真子集S，ω(G−S)≤∣S∣+1。ω(G-S) ≤ |S|+1。ω(G−S)≤∣S∣+1。
4.15 同第二次作业题9

第五章匹配

偶图的匹配问题

图的匹配与贝尔热定理

偶图

定义：所谓具有二分类（X, Y）的偶图（或二部图）是指一个图，它的点集可以分解为两个(非空)子集X和Y，使得每条边的一个端点在X中，另一个端点在Y中.
性质
- 偶图不能有环，偶图可以有重边；
- 【判定定理】 图G是偶图当且仅当G不含奇圈。
k-正则偶图
- k-正则偶图的两个顶点子集包含顶点个数相等。
对称差运算

图的匹配

匹配 M— 如果M是图G的边子集(不含环），且M中的任意两条边没有共同顶点，则称M是G的一个匹配或对集或边独立集。
饱和点 如果G中顶点v是G的匹配 M中某条边的端点，称它为M饱和点，否则为M非饱和点。
最大匹配M — 如果M是图G的包含边数最多的匹配，称M是G的一个最大匹配。特别是，若最大匹配饱和了G的所有顶点，称它为G的一个完美匹配。
区分
- 一个图G不一定存在完美匹配；
- 一个图G的完美匹配若存在，不一定唯一；
- 一个图G的最大匹配不一定唯一。
M交错路与M可扩路— 如果M是图G的匹配，G中一条由M中的边和非M中的边交错形成的路，称为G中的一条M交错路。特别地，若M交错路的起点与终点是M非饱和点，称这种M交错路为M可扩路。

贝尔热定理

定理1 最大匹配判定 (贝尔热，1957) G的匹配M是最大匹配，当且仅当G不包含M可扩路。
- 证明：
  - 必要性：非B >> 非A ，若存在M可扩路，可得更多边的匹配

- 充分性：（没看懂）:

偶图的匹配与覆盖

问题引出：两个集合，如何匹配？

偶图匹配存在性判定——Hall定理

定理2 (Hall定理）设G=(X, Y)是偶图，则G存在饱和X每个顶点的匹配(X选Y)的充要条件是：∀S⊆X,∣N(S)∣≥∣S∣⋯(∗)\forall S \subseteq X,\left| {N(S)} \right| \ge \left| S \right| \cdots (*)∀S⊆X,∣N(S)∣≥∣S∣⋯(∗)

N(S)为S的邻接顶点的集合
证明：
- 必要性：X的每个顶点，在Y中至少有一个邻接点(A>>B)
- 充分性：（反证）假设B下有非A,然后退出非B 矛盾: 存在不饱和X的顶点u，
  - 设Z为关联u的M交错路，S=X∩Z,T=Z∩YS=X∩Z , T=Z∩YS=X∩Z,T=Z∩Y,
  - S-｛u｝中点与T中点在M*下配对,$|N(S)| = |T| = |S| -1< |S| $
Hall定理也可表述为：设G=(X,Y)是偶图，如果存在X的一个子集S,使得|N(S)| < |S| ，那么G中不存在由X到Y的匹配。
又称“婚姻定理” ：在一个由r个女人和s个男人构成的人群中，1≦r≦s。在熟识的男女之间可能出现r对婚姻的充分必要条件是，对每个整数k(1≦k≦r),任意k个女人共认识至少k个男人。(女挑选男)
推论若G是k (k>0)正则偶图，则G存在完美匹配。
- 证明：k∣X∣=k∣Y∣→∣X∣=∣Y∣；k|X|=k|Y| \rightarrow |X| = |Y|；k∣X∣=k∣Y∣→∣X∣=∣Y∣；对于X的任一非空子集S, 设E1与E2分别是与S和N(S)关联的边集，显然有E1⊆E2{E_1} \subseteq {E_2}E1⊆E2则 ∣E1∣=k∣S∣≤∣E2∣=k∣N(S)∣\left| {{E_1}} \right| = k\left| S \right| \le \left| {{E_2}} \right| = k\left| {N(S)} \right|∣E1∣=k∣S∣≤∣E2∣=k∣N(S)∣
例题2
- (1) 证明：每个k方体都有完美匹配(k大于等于2)
  - 证法一：按坐标之和的奇和偶两部分 [k方体有2k2^k2k个顶点,每个顶点可以用长度为k的二进制码来表示，两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同。] >> k正则偶图 >> 存在完美匹配
  - 证法二：构造法（举例法）：
  - 一些结论： k方体是k正则偶图。
- (2) 求K2nK_{2n}K2n和Kn,nK_{n,n}Kn,n中不同的完美匹配的个数。
  - K2n=(2n−1)K2n−2K_{2n} = (2n-1)K_{2n-2}K2n=(2n−1)K2n−2 >> (2n−1)!!(2n-1)!!(2n−1)!!
  - Kn,n=n∗Kn−1,n−1K_{n,n} = n * K_{n-1,n-1}Kn,n=n∗Kn−1,n−1 >> n!n!n!
例3 证明树至多存在一个完美匹配。
- (反证+对称差)假设存在连个匹配M1,M2M1,M2M1,M2, M1ΔM2≠ΦM1ΔM2≠ΦM1ΔM2=Φ，T[M1ΔM2]T[M1ΔM2]T[M1ΔM2]每个非空部分顶点度数为2（∣M1∣=∣M2∣|M1|=|M2|∣M1∣=∣M2∣），即它存在圈，矛盾。

点覆盖与哥尼定理

点覆盖的概念与性质
- 定义1 图的点覆盖 G的一个顶点子集K称为G的一个点覆盖，如果G的每条边都至少有一个端点在K中。G的一个包含点数最少的点覆盖称为G的最小点覆盖，其包含的点数称为G的覆盖数，记为α(G).
- 定理2（点覆盖与边匹配互为上下界） 设M是G的匹配，K是G的覆盖，若|M|=|K|,则M是最大匹配，而G是最小覆盖。
  - 证明：由匹配和覆盖定义有：|M*|≦|K*|。（M每条边取点,得到的点集不一定能点覆盖（少于最小点覆盖））

哥尼定理(哥尼，1931) 在偶图中，最大匹配的边数等于最小覆盖的顶点数。

证明：反证法
最小点覆盖K∗=(X−S)∪TK* =(X-S)∪TK∗=(X−S)∪T 最大边覆盖M∗为红边集合M*为红边集合M∗为红边集合可证[K∗=M∗K*= M*K∗=M∗]（M上的每条边选一个不饱和顶点）
例4 矩阵的一行或一列称为矩阵的一条线。证明：布尔矩阵中，包含了所有“1”的线的最少数目，等于具有性质“任意两个1都不在同一条线上的1的最大数目”。
- 分析：布尔矩阵 >> 行，列分为两部分(X表示行点集合，Y表示列点集合) (0/1表示是否有边)>> 偶图 >> 哥尼定理 >> 证之

图的因子分解

托特定理(图的完美匹配存在定理)

托特定理 (托特定理，1947) 图G有完美匹配当且仅当对V的任意非空真子集S, 有：o(G−S)≤∣S∣o(G - S) \le \left| S \right|o(G−S)≤∣S∣
- 注： o(G−S)≤∣S∣o(G - S) \le \left| S \right|o(G−S)≤∣S∣ 表示奇分支数目.(奇分支：顶点数为奇数)
- 例1 证明：一棵树G有完美匹配当且仅当对所有顶点v ∈V(G),有：o (G - v)=1。
  - 证明：
    - 必要性：（A >> B）完美匹配 >> 托特定理 >> o(G - v)≤1;完美匹配 >> G 为偶阶树 >> o(G-v)≥1
    - 充分性：（B>>A）对所有顶点v ∈V(G),有：o (G - v)=1 >> 与奇分支关联的边选为匹配边(M=｛e(v):它是由v连到G-v的奇分支的边，v ∈V(G) ｝)
推论 (彼得森定理) 没有割边的3正则图存在完美匹配。
- 证明：
  - 假设设S为任意分支，mi为S与第i个奇分支连接的边数目（0<i<=k）
  - (mi = Gi在G中总度数 - Gi总度数) mi=3∣V(Gi)∣−2∣E(Gi)∣{m_i} = 3\left| {V({G_i})} \right| - 2\left| {E({G_i})} \right|mi=3∣V(Gi)∣−2∣E(Gi)∣ >> mim_imi为奇数
  - 无割边 >> mi≥3m_i \geq 3mi≥3 则 $k \le {1 \over 3}\sum\limits_{i = 1}^k {{m_i}} $
  - 对于S有， ${1 \over 3}\sum\limits_{i = 1}^k {{m_i}} \le {1 \over 3}\sum\limits_{v \in S}^{} {d(v)} $
  - 于是o(G−S)=k≤13∑i=1kmi≤13∑v∈Sd(v)≤13⋅3∣S∣=∣S∣o(G - S) = k \le {1 \over 3}\sum\limits_{i = 1}^k {{m_i}} \le {1 \over 3}\sum\limits_{v \in S}^{} {d(v)} \le {1 \over 3} \cdot 3\left| S \right| = \left| S \right|o(G−S)=k≤31i=1∑kmi≤31v∈S∑d(v)≤31⋅3∣S∣=∣S∣
  - 利用托特定理得证

图的一因子分解

基本概念

所谓一个图G的因子Gi，是指至少包含G的一条边的生成子图。
所谓一个图G的因子分解，是指把图G分解为若干个边不重的因子之并。
所谓一个图G的n因子，是指图G的n度正则因子。
如果一个图G能够分解为若干n因子之并，称G是可n因子分解的。
问题：
能否分解如何分解
图的一因子分解
一因子实际上就是图的一个完美匹配的导出子图。一个图能够作一因子分解，也就是它能够分解为若干边不重的完美匹配的导出子图之并。

定理1 K2nK_{2n}K2n可一因子分解。

证明：(给出分解方法) 轮换法 2n-1个边不重的一因子（每个拥有n条边）
例2 证明：每个k (k>0)正则偶图G是一可因子分解的。
- 证明： G存在完美匹配 >> G存在至少一个一因子 >> 设Q为G的一个一因子，G-Q仍位正则偶图 >> 递推

定理2 具有H圈的三正则图可一因子分解。

证明: 抽取H圈，剩下的边构成一个一因子 >> 三正则图（奇度点数目为偶数（握手定理）），H圈为偶圈，可分解为两个一因子。

定理3 若三正则图有割边，则它不能一因子分解。

反证假设能分解，有三个一因子，任意减去一个一因子，剩下的必然为圈之并（均为偶点，存在欧拉回路），即不能有割边

图的二因子分解

如果一个图可以分解为若干2度正则因子之并，称G可以2因子分解。
- 注意：G的一个H圈肯定是G的一个2因子，但是G的一个2因子不一定是G的H圈。2因子可以不连通。

定理4 K2n+1K_{2n+1}K2n+1可2因子分解

证明：(给出分解方法)
顶点集 V(K2n+1)={v1,v2,⋯,v2n+1}V({K_{2n + 1}}) = \left\{ {{v_1},{v_2}, \cdots ,{v_{2n + 1}}} \right\}V(K2n+1)={v1,v2,⋯,v2n+1}
作路(0<i<=n,下标需要mod2n,如n=3时 P1=v1v6v2v5v3v4{P_1} = {v_1}{v_6}{v_2}{v_5}{v_3}{v_4}P1=v1v6v2v5v3v4) Pi=vivi−1vi+1vi−2vi+2vi−3⋯vi−nvi+n{P_i} = {v_i}{v_{i - 1}}{v_{i + 1}}{v_{i - 2}}{v_{i + 2}}{v_{i - 3}} \cdots {v_{i - n}}{v_{i + n}}Pi=vivi−1vi+1vi−2vi+2vi−3⋯vi−nvi+n
生成圈Hi为v2n+1与Pi的两个端点连线。

定理5 K2nK_{2n}K2n可分解为一个1因子和n-1个2因子之和。

证明：给出分解方法：作n-1条路 Pi=vivi−1vi+1vi−2vi+2vi−3⋯vi−n−1vi+n−1{P_i} = {v_i}{v_{i - 1}}{v_{i + 1}}{v_{i - 2}}{v_{i + 2}}{v_{i - 3}} \cdots {v_{i - n - 1}}{v_{i + n - 1}}Pi=vivi−1vi+1vi−2vi+2vi−3⋯vi−n−1vi+n−1
- 下表按模2n-1计算，然后把v2n和Pi的两个端点连接，可以得到n-1个2因子，剩余为一因子。

定理6 每个没有割边的3正则图是一个1因子和1个2因子之和。

证明：没有割边的三正则图存在完美匹配M, 显然G-M为2-因子

定理7 一个连通图可2因子分解当且仅当它是偶数度正则图。

图的森林因子分解

把一个图分解为若干边不重的森林因子的和，称为图的森林因子分解。
荫度图G分解为边不重的森林因子的最少数目问题，称这个最少数目为G的荫度，记为σ(G)。
定理8 图G的荫度为：$\sigma (G) = \mathop {\max }\limits_s \left\lceil {{{{m_s}} \over {s - 1}}} \right\rceil $ 其中s是G的子图Hs的顶点数，而：ms=max⁡s{E(Hs)}{m_s} = \mathop {\max }\limits_s \left\{ {E({H_s})} \right\}ms=smax{E(Hs)}
定理9 完全图的荫度σ(Kn)=⌈n2⌉\sigma ({K_n}) = \left\lceil {{n \over 2}} \right\rceil σ(Kn)=⌈2n⌉ 完全偶图的荫度 σ(Kr,s)=⌈rsr+s−1⌉\sigma ({K_{r,s}}) = \left\lceil {{{rs} \over {r + s - 1}}} \right\rceil σ(Kr,s)=⌈r+s−1rs⌉

完全图的森林因子分解

对于K2n，将其分解为n条路Pi = vivi-1vi+1vi-2vi+2…vi-nvi+n,脚标按模2n计算。
对于K2n+1，先作n条路Pi = vivi-1vi+1vi-2vi+2…vi-nvi+n,脚标按模2n计算。在每条路外添上点v2n+1的n个森林因子；然后，v2n+1与v1,v2,…,v2n分别相连接得一星图，这是G的最后一个森林因子。（n条路 + 星图）
例8 证明：若n为偶数，且δ(G)≥n/2+1 ,则n阶单图G有3因子。
- 证明：存在H圈 >> n为偶数，H圈可分解出一个一因子Q >> G-Q 满足δ(G)≥n/2 >> G-Q仍
  存在H圈C >> C∪QC \cup QC∪Q为一个三因子

作业题

P117—118 习题4 ： 3, 4, 5，6，7，8，9
P97—99 习题4 ： 1, 3， 4, 7，8， 11， 15.
P117—118 习题5 ： 1, 2, 3, 4，10， 11， 12, 19.

匈牙利算法与最优匹配算法

匈牙利算法（偶图中寻找完美匹配）

基本问题：偶图中寻找完美匹配（|X|=|Y|）
基本思想：从任一初始匹配M0M_0M0出发，通过寻求一条M0M_0M0可扩路P，令M1=M0ΔE(P)M_1=M_0ΔE(P)M1=M0ΔE(P), 得到比M0M_0M0更大的匹配M1M_1M1(近似于迭代思想)。
M可扩路寻找方法—交错树方法
- Edmonds首先提出: 用扎根于M非饱和点u的M交错树的生长来求M可扩路。
- 定义1 设G=(X, Y), M是G的匹配，u是M非饱和点。称树H是G的扎根于点u的M交错树,如果：
  - 1. u ∈V(H)； 2) 对任意v ∈V(H), (u, v)路是M交错路。
- H是G的扎根于点u的M交错树的情形分类讨论

匈牙利算法流程【寻找完美匹配】

初始设置：设M是初始匹配。H是扎根于M非饱和点u的交错树。令：S=V(H)∩X, T=V(H)∩Y。
(a) 、若M饱和X所有顶点，停止。否则，设u为X中M非饱和顶点，置S=｛u｝,T=Φ;
(b) 、若N(S)=T, 则G中不存在完美匹配。否则设 y ∈N(S) – T.
© 若y为M饱和点，且y z ∈M, 置S=S∪｛z｝, T=T∪｛y｝,转(b)。否则，设P为M可扩路(u, y)，置M1=MΔE§，转(a).
匈牙利算法复杂度 O(∣X∣3)O(|X|^3)O(∣X∣3)
- 1. 、最多循环|X|次可以找到完美匹配；
- 1. 、初始匹配最多扩张|X|次可以找到完美匹配；
- 1. 、每次生长树的生长至多2|X|-1次。

寻找偶图最大匹配

设M是G=(X, Y)的初始匹配。
(1) 置S=Φ, T=Φ;
(2) 若X-S已经M饱和，停止；否则，设u是X-S中的一非饱和顶点，置S=S∪｛u｝。
(3) 若N(S)=T,转(5)；否则，设y ∈N(S)-T。
(4) 若y是M饱和的，设yz ∈ M,置S=S∪｛z｝, T=T∪｛y｝,转(3);否则，存在(u, y)交错路是M可扩路P,置M=MΔE§,转(1).
(5) 若X-S=Φ,停止；否则转(2).

最优匹配算法

问题定义： G=(X, Y)是边赋权完全偶图,求G一个具有最大权值的完美匹配

可行顶点标号与相等子图

可行顶点标号： 设G=(X, Y), 若对任意的x ∈X, y ∈Y,有：l(x)+l(y)≥w(xy)l(x) + l(y) \ge w(xy)l(x)+l(y)≥w(xy)
则称 l 是赋权完全偶图G的可行顶点标号。
- 初始标号：对于任意的赋权完全偶图G，均存在G的可行顶点标号。事实上，设：
  
  则 l 是G的一个可行顶点标号。
定义3 相等子图： 设 l 是赋权完全偶图G=(X, Y)的可行顶点标号，令：El={xy∈E(G)∣l(x)+l(y)=w(xy)}{E_l} = \left\{ {xy \in E(G)\left| {l(x) + l(y) = w(xy)} \right.} \right\}El={xy∈E(G)∣l(x)+l(y)=w(xy)}称Gl=G[El]G_l = G [E_l]Gl=G[El]为G的对应于l 的相等子图。
举例

最优匹配

定理设 l 是赋权完全偶图G=(X, Y)的可行顶点标号，若相等子图Gl有完美匹配M*,则M*是G的最优匹配。
- 证明：设M*是Gl的完美匹配，则：
  w(M∗)=∑e∈M∗w(e)=∑v∈V(G)l(v)w(M*) = \sum\limits_{e \in M*} {w(e)} = \sum\limits_{v \in V(G)} {l(v)} w(M∗)=e∈M∗∑w(e)=v∈V(G)∑l(v)
- 又设M是G的任一完美匹配，则：
  w(M)=∑e∈Mw(e)≤∑v∈V(G)l(v)w(M) = \sum\limits_{e \in M} {w(e)} \le \sum\limits_{v \in V(G)} {l(v)} w(M)=e∈M∑w(e)≤v∈V(G)∑l(v)
- 所以，w (M*)≥w (M)。即M*是G的最优匹配。

Kuhn最优匹配算法（第二步重新开始是指？？）

给一初始顶点标号l ,在Gl中任选一个匹配M。
(1) 若X是M饱和的，则M是最优匹配。否则，令u是一个M非饱和点，置：S=｛u｝,T=Φ。
(2) 若 NGl(S)⊃T{N_{{G_l}}}(S) \supset TNGl(S)⊃T，转(3)。否则，计算
给出新的可行顶点标号，在新标号下重新开始。（算新的相等子图）
(3) 在NGl(S)−TN_{Gl}(S)-TNGl(S)−T中选择点y。若y是M饱和的，yz ∈M,则置S=S∪｛z｝,T=T∪｛y｝转(2)。否则，设P是Gl中M可扩路，置M=MΔE§,转(1).

匹配在矩阵中的应用

矩阵与偶图
detA和GA=(X, Y)之间关系（不做要求）
例2 证明：K6n−2K_{6n-2}K6n−2有一个3因子分解。
- 证明：可以分解为6n-3个边不重的一因子之和，一因子三三组对，得到2n-1个3因子

习题(第二次作业)

P97---99    习题4 ： 1,  3， 4,  7，8， 11， 15.
P117---118    习题5 ： 1,  2, 3,  4，10， 11， 12, 19.
P117---118    习题4 ： 13

习题5：

1. 证：k立方体都有完美匹配： k正则偶图
1. 求K2n, kn,n的完美匹配个数：递推
1. k>1 举例没有完美匹配的k正则图距离：三角形（k=2,n为奇数（奇圈））

4（未解决）证明： k4有唯一的一个一因子分解，并给出K8的一个一因子分解

1. 求K3,3 和 K6的一因子分解的数目
1. 证K2n 一因子分解的数目 ((2n)!)/(2n∗n!)((2n)!)/(2^n*n!)((2n)!)/(2n∗n!)
1. 若n是偶数，且 σ(G)≥n2+1\sigma (G) \ge {n \over 2} + 1σ(G)≥2n+1，则n阶图G有3－因子。: H圈
1. 证明 K>0
- 每个k正则偶图是1-可因子分解：正则偶图存在完美匹配递推
- 每个2k正则偶图是2-可因子分解：参考解法：证存在H圈，不断减H圈
12 一棵树G有完美匹配当且仅当对所有顶点v ∈V(G),有：o (G - v)=1。
19

第六章平面图

平面图的概念和性质

问题引入：电路板设计问题导线不交叉
定义1 如果能把图G画在平面上，使得除顶点外，边与边之间没有交叉，称G可以嵌入平面，或称G是可平面图。可平面图G的边不交叉的一种画法，称为G的一种平面嵌入，G的平面嵌入表示的图称为平面图。
定义2
- (1) 一个平面图G把平面分成若干连通片，这些连通片称为G的区域，或G的一个面。G的面组成的集合用Φ表示。
- (2) 面积有限的区域称为平面图G的内部面，否则称为G的外部面。
- (3) 在G中，顶点和边都与某个给定区域关联的子图，称为该面的边界。某面 f 的边界中含有的边数(割边计算2次)称为该面 f 的次数, 记为deg ( f )。（环算一次）

定理1（次数公式）设G=(n, m)是平面图，则：∑f∈Φdeg⁡(f)=2m\sum\limits_{f \in \Phi } {\deg (f)} = 2mf∈Φ∑deg(f)=2m

证明：对G的任意一条边e, 如果e是某面割边，那么由面的次数定义，该边给G的总次数贡献2次；如果e不是割边，那么，它必然是两个面的公共边，因此，由面的次数定义，它也给总次数贡献2次。于是有： ∑f∈Φdeg⁡(f)=2m\sum\limits_{f \in \Phi } {\deg (f)} = 2mf∈Φ∑deg(f)=2m。

平面图的欧拉公式

定理2(欧拉公式) 设G=(n, m)是连通平面图，ф是G的面数，则：n−m+ϕ=2n - m + \phi = 2n−m+ϕ=2

证明：
- G 是树： m = n-1
- G不是树:
  - 断言 G不是树，存在非割边e。G-e是连通平面图，边数为m-1, 顶点数为n, 面数为ф-1。
  - 用数学归纳法证明，递推式：n−(m−1)+(ϕ−1)=2n - (m - 1) + (\phi - 1) = 2n−(m−1)+(ϕ−1)=2 >> n−m+ϕ=2n - m + \phi = 2n−m+ϕ=2

推论1 设G是具有ф个面k个连通分支的平面图，则：n−m+ϕ=k+1n - m + \phi = k + 1n−m+ϕ=k+1

证明：∑i=1kϕi=ϕ+k−1\sum\limits_{i = 1}^k {{\phi _i}} = \phi + k - 1i=1∑kϕi=ϕ+k−1

推论2（必要条件）设G是具有n个点m条边ф个面的连通平面图，如果对G的每个面f ,有：deg (f) ≥ l ≥3,则m≤ll−2(n−2)m \le {l \over {l - 2}}(n - 2)m≤l−2l(n−2)

例1 求证：K3,3是非可平面图。

推论3 设G是具有n个点m条边ф个面的简单平面图，则：m≤3n−6m \le 3n - 6m≤3n−6

证明：
- G连通，G是简单图，所以每个面的次数至少为3 有推论2
- G不连通，对于不少于3个点的连通分支成立mi<= 3ni-6，同时对于少于3个点的连通分支有 mj<=3nj, 则 mi+mj <= 3 ni + nj -6
例2，证明：K5是非可平面图。

推论4 设G是具有n个点m条边的连通平面图，若G的每个圈均由长度是 l 的圈围成，则：m(l−2)=l(n−2)m(l - 2) = l(n - 2)m(l−2)=l(n−2)

推论5 设G是具有n个点m条边的简单平面图，则：δ≤5\delta \le 5δ≤5

5色定理”的出发点。

定理3 一个连通平面图是2连通的，当且仅当它的每个面的边界是圈。

证明：（未看懂）
- 必要性：假设A >> 设非B 推出矛盾：
- 充分性：每个

推论6 若一个平面图是2连通的，则它的每条边恰在两个面的边界上。

图的嵌入性问题简介

定理4 G可球面嵌入当且仅当G可平面嵌入。

证明：建立球极平面射影

定理5（三维空间嵌入）所有图均可嵌入R3中。

证明：
对处于曲线 l 上的任意4个相异顶点，它们对应的参数值分别为：t1,t2,t3,t4。4点不共面。

凸多面体与平面图

凸多面体的一维骨架：把一个凸多面体压缩在平面上，得到一个对应的平面图，该平面图称为该凸多面体的一维骨架。

定理6 存在且只存在5种正多面体：它们是正四、六、八、十二、二十面体。

特殊平面图与平面图的对偶图

特殊平面图

极大平面图及其性质

定义1 设G是简单可平面图，如果G是Ki (1≦i≦4),或者在G的任意非邻接顶点间添加一条边后，得到的图均是非可平面图，则称G是极大可平面图。
- 注：只有在单图前提下才能定义极大平面图。
引理设G是极大平面图，则G必然连通；且若G的阶数大于等于3，则G无割边。
- 证明：反证

定理1 设G是至少有3个顶点的平面图，则G是极大平面图，当且仅当G的每个面的次数是3且为单图。

证明：反证
推论：设G是n个点，m条边和ф个面的极大平面图，且n≥3.则：(1) m=3n-6; (2) ф=2n-4.
- 证明：
注：顶点数相同的极大平面图并不唯一。
**定义2 极小不可平面图 **如果在不可平面图G中任意删去一条边所得的图为可平面图，则称G为极小不可平面图。

外可平面图

定义3 外可平面图 若一个可平面图G存在一种平面嵌入，使得其所有顶点均在某个面的边界上，称该图为外可平面图。外可平面图的一种外平面嵌入，称为外平面图。
- 注：对外可平面图G来说，一定存在一种外平面嵌入，使得G的顶点均在外部面的边界上。这由球极投影法可以说明。
定义4 极大外可平面图 设G是一个简单外可平面图，若在G中任意不邻接顶点间添上一条边后，G成为非外可平面图，则称G是极大外可平面图。极大外可平面图的外平面嵌入，称为极大外平面图。
引理设G是一个连通简单外可平面图，则在G中存在度数至多是2的顶点。(证明略)

定理2 设G是一个有n (n≥3)个点，且所有点均在外部面上的极大外平面图，则G有n-2个内部面。

证明：数学归纳法：G-u(u为度为2的点（极大外平面图一定存在）)

定理3 设G是一个有n (n≥3)个点，且所有点均在外部面上的外平面图，则G是极大外平面图，当且仅当其外部面的边界是圈，内部面是三角形。

证明：
- 必要性：
  - 外部面 >> 必须闭迹（不然存在割边，不满足极大性） >> 非圈的闭迹可添加边 >> 必须是圈
  - 内部面 >> 必须是圈(外部面是生成圈，G是2连通的)(简单图圈长必须大于等于3) >> 假设某个面边大于3,z则可添边 >> 必须小于等于3
- 充分性： B >> A :假设B,如果不是极大,则可添边 >> 内部，外部添边不可性 >> 是极大

定理4 每个至少有7个顶点的外可平面图的补图不是外可平面图，且7是这个数目的最小者。

平面图的对偶图(面映射到点)

定义4 对偶图 给定平面图G，G的对偶图G*如下构造：
- (1) 在G的每个面fi内取一个点vi作为G的一个顶点；
- (2) 对G的一条边e, 若e是面 fi 与 fj 的公共边，则连接vi与vj，且连线穿过边e;若e是面 fi 中的割边，则以vi为顶点作环，且让它与e相交。

平面图的对偶图也是平面图

应用
- 面着色转变为顶点着色
对偶图的性质
- 1. G*的顶点数等于G的面数；
- 1. G*的边数等于G的边数；
- 1. G*的面数等于G的顶点数；
- 1. d (v*)=deg( f )

定理5 平面图G的对偶图必然连通

证明：
- 证明连通性：在G中任意取两点vi与vj*。我们证明该两点连通即可！
(G*)*不一定等于(同构于)G;
G是平面图，则(G∗)∗≅G(G*)* \cong G(G∗)∗≅G，当且仅当G是连通的。(习题第26题)
- 证明：
  - 必要性： G* 连通 >> (G*)* 连通 >> G 连通
  - 充分性：映射
    - 由对偶图的定义知，平面图G与其对偶图G*嵌入在同一平面上，当G连通时，容易知道：G*的无界面 f **中仅含G的唯一顶点v,而除v外，G中其它顶点u均与G*的有限面形成一一对应，于是，G中顶点和G**顶点在这种自然对应方式下一一对应，且对应顶点间邻接关系保持不变
辨析：
- 同构的平面图可以有不同构的对偶图。

P143—146 习题5 ：3，4，5，6，8， 25, 26，27。其中 25，26，27结合课件学习。

5.25 证明：
- (1) B是平面图G的极小边割集，当且仅当{c∗∈E(G∗)∣c∈B}=C∗\left\{ {c* \in E(G*)\left| {c \in B} \right.} \right\} = C*{c∗∈E(G∗)∣c∈B}=C∗ 是G*的圈。（！！搞不懂）
  - 证明：
    - 必要性：数学归纳法
    - 充分性：反证法
- (2) 欧拉平面图的对偶图是偶图。
  - 因欧拉图的任意边割集均有偶数条边。于是由(1),G*中不含奇圈。所以G*是偶图。
5.26 见定理5 证明
5.27 设T是连通平面图G的生成树，E∗={e∗∈E(G∗)∣e∉E(T)}E* = \left\{ {e* \in E(G*)\left| {e \notin E(T)} \right.} \right\}E∗={e∗∈E(G∗)∣e∈/E(T)}证明：T*=G*[E*]是G*中的生成树。(!!放弃)
- 证明：
  - 情形1，如果G是树。
  - 情形2，如果G不是树。
    - 因G的每个面必然含有边e不属于E(T),即G*的每个顶点必然和E*中的某边关联>>T*必然是G*的生成子图。
    - T*中没有圈

平面图的判定与涉及平面性不变量

平面图的判定

方法
- 观察法
- 利用相关特性 1. m <= l(n-2)/(l-2) (deg(f)>=l)
定义 2度顶点内收缩 在图G的边上插入一个2度顶点，使一条边分成两条边，称将图在2度顶点内扩充；去掉一个图的2度顶点，使关联它们的两条边合并成一条边，称将图G在2度顶点内收缩。
定义2 同胚 两个图G1与G2说是同胚的，如果G1≅G2{G_1} \cong {G_2}G1≅G2，或者通过反复在2度顶点内扩充和收缩后能够变成一对同构的图。

定理1 (库拉托斯基定理) 图G是可平面的，当且仅当它不含K5和K3,3同胚的子图。

等价库拉托斯基定理：图G是非可平面的，当且仅当它含有K5或K3,3同胚的子图
定义3 基础简单图 给定图G, 去掉G中的环，用单边代替平行边而得到的图称为G的基础简单图。

定理2 (1) 图G是可平面的，当且仅当它的基础简单图是可平面的；(2) 图G是可平面图当且仅当G的每个块是可平面图

证明：
- (1)显然
- (2) 充分性显然，必要性: 数学归纳法，前k-1块成立， k块也成立
定义4 初等收缩 设uv是简单图G的一条边。去掉该边，重合其端点，再删去由此产生的环和平行边。这一过程称为图G的初等收缩或图的边收缩运算。

定理2 (瓦格纳定理)：简单图G是可平面图当且仅当它不含有可收缩到K5或K3,3的子图。

例3 求证彼得森图是非可平面图。：收缩成k5

定理3 至少有9个顶点的简单可平面图的补图是不可平面的，而9是这个数目中的最小的一个。

例4 找出一个8个顶点的可平面图，使其补图也是可平面的。
例5 设G是一个简单图，若顶点数n≥11,则G与G的补图中，至少有一个是不可平面图 (要求用推理方法).
- 证明： m <= 3n- 6 略
例6 设Gi是一个有ni个点，mi条边的图，i=1,2。证明：若G1与G2同胚，则：n1+m2=n2+m1{n_1} + {m_2} = {n_2} + {m_1}n1+m2=n2+m1
- 证明：直接运算

涉及平面性的不变量 [了解性内容]

问题引入：如何刻画一个非可平面图与平面图之间的差距。

P143—146 习题5 ：6，7，8，11、12。

平面性算法

涉及算法的相关概念

平面性的判定

(1) 对于简单图G=(n, m)，如果m>3n-6，则G是非可平面的；
(2) 对于简单连通图G=(n, m)，如果每个面次数至少为l≥3,且m>(n-2)l /(l-2)，则G是非可平面的；
(3) 库拉托斯基定理：G是可平面的当且仅当G不含有与K5和K3,3同胚的子图；
(4) 瓦格纳定理：G是可平面的当且仅当G不含有能够收缩成K5和K3,3的子图；

定理1(可平面的必要条件) 设H~\tilde HH~是G容许的，则对于H的每座桥B:F(B,H~)≠ΦF(B,\tilde H) \ne \Phi F(B,H~)=Φ

证明：
注：定理1实际上给出了一个图是可平面图的一个必要条件。如果存在G的一个可平面子图H,使得对于某桥B，有F(B,H~)=ΦF(B,\tilde H){\rm{ = }}\PhiF(B,H~)=Φ，那么，G是非可平面的。

平面性算法（DMP算法）

设G是至少三个顶点的简单块。
(1) 取G的一个圈H1,求出H1的一个平面嵌入H1~\tilde{H_1}H1~。置i=1;
(2) 若E(G)-E(Hi)=Φ,则停止；否则，确定G中Hi的所有桥，并对每座桥B，求出F(B,H~i)F(B,{\tilde H_{\rm{i}}})F(B,H~i)
(3) 若存在桥B,使得：$F(B,{\tilde H_{\rm{i}}}) = \Phi ，则停止(G不可平面)；否则，在Hi的所有桥中确定一个使得，则停止 (G不可平面) ；否则，在Hi的所有桥中确定一个使得，则停止(G不可平面)；否则，在Hi的所有桥中确定一个使得\left| {F(B,{{\tilde H}_{\rm{i}}})} \right|$最小的B，并取 f∈F(B,H~i)f \in F(B,{\tilde H_i})f∈F(B,H~i)。
(4) 在桥B中取一条连接Hi中两个附着顶点的路Pi, Pi⊆Bi{P_i} \subseteq {B_i}Pi⊆Bi，置Hi+1=Hi∪Pi,把Pi画在H~i{\tilde H_{\rm{i}}}H~i面 f 内,得到H~i+1{\tilde H_{{\rm{i + 1}}}}H~i+1
(5) 置i=i+1转(2)。

第六章习题

P143—146 习题5 ：6，7，8，11、12。
P143—146 习题5 ：3，4，5，6，8， 25, 26，27。其中 25，26，27结合课件学习。
6.1 判断图6-38所示的七个图是否可平面图？为什么？

判定问题：
- 根据性质判定：(一般可以判定是非可平面图)
- (1) 对于简单图G=(n, m)，如果m>3n-6，则G是非可平面的；
- (2) 对于简单连通图G=(n, m)，如果每个面次数至少为l≥3,且m>(n-2)l /(l-2)，则G是非可平面的；
- (3) 库拉托斯基定理：G是可平面的当且仅当G不含有与K5和K3,3同胚的子图；
- (4) 瓦格纳定理：G是可平面的当且仅当G不含有能够收缩成K5和K3,3的子图；
- 用平面性算法,求出一种平面嵌入
6.2
6.3 设G是有n个点ф个面的简单连通平面图，n≥3。证明：ф≤2n-4。
6.4 设G是一个有n（n>3）个点m条边ф个面的极大平面图,则
(1) m = 3n-6；
(2) ф= 2n-4;
(3) κ(G)≥3;（未解决）
(4) δ(G)≥3; （未解决）
(5) G中至少有4个顶点的度不超过5。

解：
(1) 极大平面图每个面的次数为为3 次数公式 + 欧拉公式 >> m = 3n - 6
(2) 次数公式
(3) 定义法？？(未解决)： n>3的G为极大平面图，每个面由三条边组成，且每个顶点v由d(v)>=3,对于G中任一顶点或者子图，至少与三个领点与之相邻，要使得G中任意一个分支或点分离(w(G-H)>w(G))，需要至少去掉三个点，即K(G)>=3.
6.5 设G是一个有n个点m条边的简单连通可平面图,且满足m = 3n-6，则G是极大可平面图。

证明：思路：（非B 推出非A）: 假设G不是极大可平面图，则存在e使得，G+e仍是可平面图，G+e的边数未m+1 > 3n -6 则G+e不满足可平面图的条件，矛盾，假设不成立。
6.6 对一个n阶极大平面图G。试证：
（1）若δ(G) = 4，则n≥6，且G中至少有6个顶点的度不超过5；
（2）若δ(G) = 5，则n≥12，且G中至少有12个顶点的度为5。

解：反证法
(1) 握手定理 + 欧拉 >> n>=6, 假设至多5个顶点度不超过5,则 2m = 度数和 >= 5*5 +(n-5)*6 则 m > 3n -2.5 > 3n - 6
(2) 同（1）
6.7 试证：在有6个顶点、12条边的简单连通平面图中，每个面均由3条边围成。

证法一：若存在某个面由4条边组成，则该面中可添加一条边使得G+e仍为平面图，而G+e的边数为13> 3n-6 = 12，矛盾，假设不成立
证法二：根据欧拉定理：n-m+r= 2 则r = 8（8个面），若存在面的次数大于3，则根据次数公式 2m = 面次数之和 > 3r,即 24 > 24 ，矛盾，假设不成立。
6.8 证明：
（1）证明：若G是点数n≥4的极大平面图，则G中每个点的度数至少为3。
（2）证明：若G是点数n≥3的简单连通平面图，则G中至少有三个度数小于等于5的点。
（3）证明：若G是点数n≥4的简单连通平面图，则G中至少有四个度数小于等于5的点。

（1）（未解决）
（2）反证
（3）反证
6.9 试证：若G是连通平面图，且所有顶点的度数不小于3，则G至少有一个面f，使得deg（f）≤5。

反证次数公式 + 欧拉公式 + 握手定理导出矛盾
6.10 用平面性算法判定图6-42中图G1 ,G2和G3的平面性。
6.11 n>=11 则G与G的补图至少一个为不可平面图
6.12 图的厚度相关问题
6.25 证明：
(1) B是平面图G的极小边割集，当且仅当{c∗∈E(G∗)∣c∈B}=C∗\left\{ {c* \in E(G*)\left| {c \in B} \right.} \right\} = C*{c∗∈E(G∗)∣c∈B}=C∗ 是G*的圈。（！！搞不懂未解决）
(2)欧拉平面图的对偶图是偶图

(1) 证明：
- 必要性：数学归纳法
- 充分性：反证法
- (2) 欧拉平面图的对偶图是偶图。
- 因欧拉图的任意边割集均有偶数条边。于是由(1),G*中不含奇圈。所以G*是偶图。
6.26 见定理5 证明

证明：
- 证明连通性：在G中任意取两点vi与vj*。我们证明该两点连通即可！
- (G*)*不一定等于(同构于)G;
- G是平面图，则(G∗)∗≅G(G*)* \cong G(G∗)∗≅G，当且仅当G是连通的。(习题第26题)
- 证明：
- 必要性： G* 连通 >> (G*)* 连通 >> G 连通
- 充分性：映射
- 由对偶图的定义知，平面图G与其对偶图G*嵌入在同一平面上，当G连通时，容易知道：G*的无界面 f **中仅含G的唯一顶点v,而除v外，G中其它顶点u均与G*的有限面形成一一对应，于是，G中顶点和G**顶点在这种自然对应方式下一一对应，且对应顶点间邻接关系保持不变
6.27 设T是连通平面图G的生成树，E∗={e∗∈E(G∗)∣e∉E(T)}E* = \left\{ {e* \in E(G*)\left| {e \notin E(T)} \right.} \right\}E∗={e∗∈E(G∗)∣e∈/E(T)}证明：T*=G*[E*]是G*中的生成树。(!!放弃)

证明：
- 情形1，如果G是树。
- 情形2，如果G不是树。
- 因G的每个面必然含有边e不属于E(T),即G*的每个顶点必然和E*中的某边关联>>T*必然是G*的生成子图。
- T*中没有圈

第七章图的着色

图的边着色

几类特殊图的边色数

偶图的边色数

定理一完全偶图 $\chi '({K_{m,n}}) = \Delta $

证明设Δ=n
- 证：χ′(Km,n)≤n\chi '({K_{m,n}}) \le nχ′(Km,n)≤n，给出一种着色方案：
  ∀xiyj∈E(Km,n),π(xiyj)=(i+j)(modn)\forall {x_i}{y_j} \in E({K_{m,n}}),\pi ({x_i}{y_j}) = (i + j)(\bmod n)∀xiyj∈E(Km,n),π(xiyj)=(i+j)(modn)
  对任意邻边都有 π(xiyj)≠π(xiyk)\pi ({x_i}{y_j}) \neq \pi ({x_i}{y_k})π(xiyj)=π(xiyk)
- χ′(Km,n)≥Δ=n\chi '({K_{m,n}}) \ge \Delta = nχ′(Km,n)≥Δ=n显然
- 则 $\chi '({K_{m,n}}) = \Delta $
定义3 缺色 设п是G的一种正常边着色，若点u关联的边的着色没有用到色i，则称点u缺i色。

定理2 (哥尼，1916)若G是偶图，则边色数为最大度，即 χ′(G)=Δ\chi '(G) = \Delta χ′(G)=Δ

证明：数学归纳法（对G的边数m做数学归纳）
- m=1 成立
- 考虑G1=G−uvG1=G-uvG1=G−uv有符合条件的着色方案，则χ′(G1)=Δ(G1)≤Δ(G)\chi '({G_1}) = \Delta ({G_1}) \le \Delta (G)χ′(G1)=Δ(G1)≤Δ(G)
  - G 通过G1的着色方案后，仍有uv未着色(未解决)
    - 情形1 u,v可缺同一种颜色i，对u,v着i色，χ′(G)=Δ(G1)=Δ(G)\chi '({G}) = \Delta ({G_1}) = \Delta (G)χ′(G)=Δ(G1)=Δ(G)
    - 情形2 u,v缺不同的颜色，u缺·但v不缺，v缺·但u不缺：
      - PPT思路做局部调整：设H (i, j) 表示G1中由i色边与j色边导出的子图。因v缺色j, 但不缺色i,H(i ,j)中含v的分支是一条路P。P不含点u(如果P含有点u, 那么P必然是一条长度为偶数的路),可以交换P中着色，而不破坏G1的正常边着色。但交换着色后，u与v均缺色i, 于是由情形1,可以得到G的Δ正常边着色.
      - 个人理解 添新色: 若u,v是最大度点（因为u,v不能缺同一种颜色，所以u,v一定有一个是最大度点），则新增色k，uv着k色, χ′(G)=Δ(G1)+1=Δ(G)\chi '({G}) = \Delta ({G_1})+1 = \Delta (G)χ′(G)=Δ(G1)+1=Δ(G)
      - 其他思路 见例题6： Δ\DeltaΔ 正则偶图 >> Δ\DeltaΔ个匹配 >> 可Δ\DeltaΔ边着色 >> 原图可Δ\DeltaΔ作色

一般简单图的边色数

引理：设G是简单图，x与y1是G中不相邻的两个顶点，`п`是G的一个正常k边着色。若对该着色`п`，x,y1以及与x相邻点均至少缺少一种颜色(没有要求同一种颜色)，则G+xy1是k边可着色的。

定理3 (维津定理，1964) 若G是单图，则：χ′(G)=Δ或χ′(G)=Δ+1\chi '(G) = \Delta 或 \chi '(G) = \Delta {\rm{ + 1}}χ′(G)=Δ或χ′(G)=Δ+1

证明：只需证明χ′(G)≤Δ+1\chi '(G) \le \Delta {\rm{ + 1}}χ′(G)≤Δ+1
对G的边数m作数学归纳
- m= 1成立
- 设G1=G−xyG1=G-xyG1=G−xy成立，即χ′(G1)≤Δ(G1)+1≤Δ(G)+1\chi '({G_1}) \le \Delta ({G_1}){\rm{ + 1}} \le \Delta {\rm{(G) + 1}}χ′(G1)≤Δ(G1)+1≤Δ(G)+1
- 存在G1的Δ(G)+1正常边作色п。显然G1的每个顶点都至少缺少一种颜色。根据引理知G1+xy是Δ(G)+1可着色的。即证明：χ′(G)≤Δ(G)+1\chi '(G) \le \Delta (G){\rm{ + 1}}χ′(G)≤Δ(G)+1

三类特殊简单图的边色数

定理4 设G是单图且Δ(G)>0。若G中只有一个最大度点或恰有两个相邻的最大度点，则：χ′(G)=Δ(G)\chi '(G) = \Delta (G)χ′(G)=Δ(G)

证明：维津定理： χ′(G)≤Δ+1\chi '(G) \le \Delta {\rm{ + 1}}χ′(G)≤Δ+1
- 只有一个最大度点,设未u： u与任意邻点v有边uv,则G-uv(最大度减一)显然可Δ\DeltaΔ着色，由于u的其他邻点(度小于Δ\DeltaΔ)显然缺色，则由引理可知，添加uv仍可Δ\DeltaΔ着色。
- 恰有两个相邻的最大度点，设为u,v，显然，由维津定理，G-uv(最大度减一)可 Δ\DeltaΔ着色，u的每个邻点(度小于Δ\DeltaΔ)缺色，则添加uv仍可Δ\DeltaΔ着色。

定理5 设G是单图。若点数n=2k+1n=2k+1n=2k+1且边数m>kΔm>kΔm>kΔ,则：χ′(G)=Δ(G)+1\chi '(G) = \Delta (G) + 1χ′(G)=Δ(G)+1

证明：设п是G的Δ(G)正常边着色方案，对于G的每个色组来说，包含的边数至多(n-1)/2=k(一条边配两个顶点，又n为奇数所以减一)。这样：m(G)≤Δkm(G) \le \Delta km(G)≤Δk，与条件矛盾。

定理6 设G是奇数阶Δ正则单图,若Δ>0,则：χ′(G)=Δ(G)+1\chi '(G) = \Delta (G) + 1χ′(G)=Δ(G)+1

证明：定理5 可证
例4 n= 2k+1 :χ′(Cn)=2+1=3\chi '({C_n}) = 2 + 1 = 3χ′(Cn)=2+1=3 , χ′(Kn)=(n−1)+1=n\chi '({K_n}) = (n - 1) + 1 = nχ′(Kn)=(n−1)+1=n
例5 求出彼得森图的边色数。

例题6 证明偶图的边色数为最大度

(1) 设G=(X, Y)是一个最大度为Δ的偶图，求证，G是某个Δ正则偶图 G*的子图。
(2) 用(1) 证明：偶图的边色数等于其最大度。
- 证：
- （1）构造法：两部分（X+Y与Y+X）当 d(xi)<Δ且d(yi)<Δ时，连接xi,yi
- （2）由(1) 对于任意最大度为Δ的偶图G,均存在G的Δ正则母图G*。又由于正则偶图存在1因子分解，所以，G*可以划分为Δ个1因子，从而其边色数为Δ。这样G的边色数也为Δ。

例7 证明：每个哈密尔顿3正则图都有泰特(Tait)着色。3正则图的正常3边着色称为泰特着色。
- 证明：设G是3正则H图，C是G的一个H圈，则C是偶圈，所以C是2可正常边着色的。因G-C是G的一个1因子，所以，可1正常边着色。因此，G是可以3边正常着色的，即G有泰特着色。

边着色的应用

例1 (排课表问题)

在一个学校中，有7个教师12个班级。在每周5天教学日条件下，教课的要求由如下矩阵给出：

其中，pij表示xi必须教yj班的节数。求：
(1) 一天分成几节课，才能满足所提出的要求？
(2) 若安排出每天8节课的时间表，需要多少间教室？

问题分析：
一节课对应边正常着色的一个色组。(色组内的不同边代表并行（同时）存在) 。
由于G是偶图，所以边色数为G的最大度35。
这样，最少周总课时为35节课。平均每天要安排7节课。
如果每天安排8节课，因为G的总边数为240，所以需要的教室数为240/40=6 （教室数代表并行容量）

例2 (比赛安排问题)

Alvin (A)曾邀请3对夫妇到他的避暑别墅住一个星期。他们是：Bob和Carrie , David和Edith, Frank和Gena。由于这6人都喜欢网球运动，所以他们决定进行网球比赛。6位客人的每一位都要和其配偶之外的每位客人比赛。另外，Alvin将分别和David， Edith， Frank， Gena进行一场比赛。若没有人在同一天进行2场比赛，则要在最少天数完成比赛，如何安排？

问题分析：
用边连接关系表示两者需要进行比赛。
对图进行边着色，一个色组表示并行的比赛
度序列为{4,4,4,5,5,5,5} ,m=16 > ((7-1)/2) *5 则需要边色数为6 即总共需要6个色组（6个场次（每个场次可同时进行多场））
每个色组平均有 m/6 <= 3。
没有人在同一天进行2场比赛，则每天安排1场次，总共6天

P187—190 习题7 ：1----6

图的顶点着色

图的点着色的几个结论

定理1 对任意的图G，有：χ(G)≤Δ(G)+1\chi (G) \le \Delta (G) + 1χ(G)≤Δ(G)+1

证明：数学归纳法(对点数作数学归纳)
- n = 1时显然成立
- 假设 G1= G -v 成立，即 χ(G1)≤Δ(G1)+1≤Δ(G)+1\chi ({G_1}) \le \Delta ({G_1}) + 1 \le \Delta (G) + 1χ(G1)≤Δ(G1)+1≤Δ(G)+1
- 设п是G1的一种Δ(G)+1正常点着色方案，因为v的邻点在п下至多用去Δ(G)种色，所以给v染上其邻点没有用过的色，就把п扩充成了G的Δ(G)+1着色方案。

G的Δ(G)+1正常点着色算法

设G=(V, E), V=｛v1,v2,…,vn｝,色集合C=｛1,2,…,Δ+1｝,着色方案为п。
(1) 令п(v1)=1, i=1;
(2) 若i=n,则停止；否则令：C(vi+1)={π(vj)∣j≤i,并且vj与vi+1相邻}C({v_{i + 1}}) = \left\{ {\pi ({v_j})\left| {j \le i,并且{v_j}与{v_{i + 1}相邻}} \right.} \right\}C(vi+1)={π(vj)∣j≤i,并且vj与vi+1相邻}
设k为C-C(vi+1)中的最小整数，令π(vi+1)=k\pi ({v_{i{\rm{ + 1}}}}){\rm{ = }}kπ(vi+1)=k
(3) 令i=i+1,转(2)。
注：不能通过上面算法求出色数
- 优化(Welsh—Powell)：最大度优先策略按顶点度数由大到小的次序着色。

定理2(布鲁克斯，1941) 若G是连通的单图，并且它既不是奇圈，又不是完全图，则：

χ(G)≤Δ(G)\chi (G) \le \Delta (G)χ(G)≤Δ(G)

定义3 次大度 设G是至少有一条边的简单图，定义：

其中N(u)为G中点u的邻域。称Δ2(G)为G的次大度。
如果[{V_2}(G) = \left{ {v\left| {v \in V(G),N(v)ud(u) \geqslant d(v)} \right.} \right}] 那么Δ2(G)=max⁡{d(v)∣v∈V2(G)}{\Delta _2}(G) = \max \left\{ {d(v)\left| {v \in {V_2}(G)} \right.} \right\}Δ2(G)=max{d(v)∣v∈V2(G)}
注：由次大度的定义知：Δ2(G)≦Δ(G)

定理3 设G是非空简单图，则：χ(G)≤Δ2(G)+1\chi (G) \le {\Delta _2}(G) + 1χ(G)≤Δ2(G)+1

推论：设G是非空简单图，若G中最大度点互不邻接，则有：χ(G)≤Δ(G)\chi (G) \le \Delta (G)χ(G)≤Δ(G)

四色与五色定理

定理4 (希伍德) 每个平面图是5可着色的。

证明（了解性内容）：对顶点作数学归纳
n=1 成立
假设n=k成立，考虑n=k+1的连通平面图G。因G是连通平面图，所以δ(G)≦5 （欧拉公式推论5）
设d(u)=δ(G)≦5。
令G1=G – u。由归纳假设，G1是5可顶点正常着色的。设п是G1的5着色方案。
(1) 如果d(u)=δ(G)<5, 显然п可以扩充为G的5正常顶点着色；
(2) 如果d(u)=δ(G) = 5, 分两种情况讨论。
- 情形1 在п下，如果u的邻接点中，至少有两个顶点着相同颜色，则容易知道，п可以扩充为G的5正常顶点着色；
- 情形2 在п下，设u的邻接点中，5个顶点着了5种不同颜色。
  - 作局部调整：不失一般性，设п(xi)=i (1≦i≦5)。设H (i, j)表示着i和j色的点在G1中的点导出子图。
    - 如果x1与x3属于H(1, 3) 的不同分支。则通过交换含x1的分支中的着色顺序，可得到G1的新正常点着色方案，使x1与x3着同色，于是由情形1，可以得到G的5正常顶点着色方案；
    - 设x1与x3属于H(1, 3) 的相同分支。
      在上面假设下，x2与x4必属于H(2, 4) 的不同分支。否则，将会得到H(1, 3) 与H(2, 4) 的交叉点。因此，п可以扩充为G的5正常顶点着色。

顶点着色的应用（重点）

图的正常顶点着色对应的实际问题是“划分”问题。

例1 课程安排问题：

某大学数学系要为这个夏季安排课程表。所要开设的课程为：图论(GT), 统计学(S),线性代数(LA), 高等微积分(AC), 几何学(G), 和近世代数(MA)。现有10名学生(如下所示)需要选修这些课程。根据这些信息，确定开设这些课程所需要的最少时间段数，使得学生选课不会发生冲突。(学生用Ai表示）
A1: LA, S ; A2: MA, LA, G ; A3: MA, G, LA;
A4: G, LA, AC ; A5: AC, LA, S ; A6: G, AC;
A7: GT, MA, LA ; A8: LA,GT, S ; A9: AC, S, LA;

分析：

建模：顶点着色问题：顶点>课程连线>约束：找出冲突约束（同一学生想上的课程不能在同一时段）

解题：
(1) 利用相关定理确定点色数的范围：
a. 下界：找特殊子图如奇圈(3)，完全图(Kn至少需要n色)等
b. 上界：相关定理
(2) 求出着色方案

例2 交通灯的相位设置问题：

如图所示，列出了繁华街道路口处的交通车道L1,L2,…,L9。在此路口处安置了交通灯。当交通灯处于某个相位时，亮绿灯的车道上的车辆就可以安全通过路口。为了(最终)让所有的车辆都能够安全通过路口，对于交通灯来说，所需要的相位的最小数是多少？

分析：

建模：顶点>>车道，连线>>冲突约束：两个车道不能同时同行。
求解：最小相位数？点色数（每个色组的车道可以同时通行）
(1) 利用相关定理确定点色数的范围：
a. 下界：找特殊子图如奇圈(3)，完全图(Kn至少需要n色)等
b. 上界：相关定理
(2) 求出着色方案

P187—190 习题7 ：7----9

与色数有关的几类图和完美图（考试不做要求）

着色的计数色多项式

色多项式概念

所谓色多项式，就是给定标定图G和颜色数k,求出正常顶点着色的方式数。方式数用Pk(G)P_k(G)Pk(G)表示。可以证明：Pk(G)是k的多项式，称为图G的色多项式。
由点色数χ(G)\chi (G)χ(G)和色多项式Pk(G)的定义可得：
- (1) 若k<χ(G)k < \chi (G)k<χ(G)，则Pk(G)=0 ;（χ(G)=min⁡{k∣Pk(G)≥1}\chi (G) = \min \left\{ {k\left| {{P_k}(G) \ge 1} \right.} \right\}χ(G)=min{k∣Pk(G)≥1}）
- (2) 若G为空图()，则Pk(G)=knP_k(G)=k^nPk(G)=kn。
- (3) Pk(Kn)=k(k−1)…(k−n+1)Pk(Kn)=k(k-1)…(k-n+1)Pk(Kn)=k(k−1)…(k−n+1)。

色多项式的两种方法

递推计数法

定理1 设G为简单图，则对任意e∈E(G)e \in E(G)e∈E(G)有：Pk(G)=Pk(G−e)−Pk(Ge){P_k}(G) = {P_k}(G - e) - {P_k}(Ge)Pk(G)=Pk(G−e)−Pk(Ge)

证明：设e=uv。则对G-e的着色方式数可以分为两部分：
(1) u与v着不同颜色。此时，等于G的着色方式数；
(2) u与v着同色。此时，等于G·e 的着色方式数；(要减去此种情况)
所以，得：Pk(G)=Pk(G−e)−Pk(Ge){P_k}(G) = {P_k}(G - e) - {P_k}(Ge)Pk(G)=Pk(G−e)−Pk(Ge)
推论：设G是单图，e=uv是G的一条边，且d(u)=1,则：Pk(G)=(k−1)Pk(G−u){P_k}(G) = (k - 1){P_k}(G - u)Pk(G)=(k−1)Pk(G−u)
- 证明：因为G是单图，e=uv, d(u)=1,所以G·e = G-u。
- 另一方面，Pk(G-e)=kPk(G-u)
- 所以Pk(G)=Pk(G−e)−Pk(Ge){P_k}(G) = {P_k}(G - e) - {P_k}(Ge)Pk(G)=Pk(G−e)−Pk(Ge)=kPk(G−u)−Pk(G−u)= k{P_k}(G - u) - {P_k}(G - u)=kPk(G−u)−Pk(G−u)=(k−1)Pk(G−u)= (k - 1){P_k}(G - u)=(k−1)Pk(G−u)

注：对递推公式的使用分析：

(1) 当图G的边数较少时，使用减边递推法：Pk(G)=Pk(G−e)−Pk(Ge){P_k}(G) = {P_k}(G - e) - {P_k}(Ge)Pk(G)=Pk(G−e)−Pk(Ge)
(2) 当图G的边数较多时，使用加边递推法：Pk(G−e)=Pk(G)+Pk(Ge){P_k}(G - e) = {P_k}(G) + {P_k}(Ge)Pk(G−e)=Pk(G)+Pk(Ge)
注：递推计数法的计算复杂度是指数型的。

理想子图计数法

定义1 理想子图：设H是图G的生成子图。若H的每个分支均为完全图，则称H是G的一个理想子图。用Nr(G)N_r(G)Nr(G)表示G的具有 r 个分支的理想子图的个数。
最大团大小为2的匹配
例题

定理2 设q r (G)表示将单图G的顶点集合V划分为 r 个不同色组的色划分个数，则：qr(G)=Nr(Gˉ).....(1≤r≤∣V∣){q_r}(G) = {N_r}(\bar G).....(1 \le r \le \left| V \right|)qr(G)=Nr(Gˉ).....(1≤r≤∣V∣)

证明：（未解决）
- 一方面，设G的任一r色划分为：｛V1,V2,…,Vr｝。于是，对于1≦i≦r,Gˉ[Vi]\bar G\left[ {{V_i}} \right]Gˉ[Vi]是Gˉ\bar GGˉ的完全子图。因为Vi∩Vj=Φ(i≠j),所以$\bigcup\limits_{i = 1}^r {\bar G[{V_i}]} 是是是\bar G$的理想子图。
- 另一方面，对于Gˉ\bar GGˉ的任一具有r个分支的理想子图，显然它唯一对应G中一个r色组。所以，我们得到：qr(G)=Nr(Gˉ).....(1≤r≤∣V∣){q_r}(G) = {N_r}(\bar G).....(1 \le r \le \left| V \right|)qr(G)=Nr(Gˉ).....(1≤r≤∣V∣)
用k种颜色对单图G正常着色，可以这样来计算着色方式数：色组为1的方式数+色组为2的方式数+…+色组为n的方式数。即有如下计数公式：Pk(G)=∑i=1nNi(Gˉ)[k]i,其中[k]i=k(k−1)(k−2)...(k−i+1){P_k}(G) = \sum\limits_{i = 1}^n {{N_i}(\bar G){{[k]}_i}} ,其中{[k]_i} = k(k - 1)(k - 2)...(k - i + 1)Pk(G)=i=1∑nNi(Gˉ)[k]i,其中[k]i=k(k−1)(k−2)...(k−i+1)
定义2 ：设G是单图，令Ni(G)=ri , [k]i=xi 。称$h(G,x) = \sum\limits_{i = 1}^n {{r_i}{x^i}} $为图G的伴随多项式。
于是，求Pk(G)就是要求出 Gˉ\bar GGˉ的伴随多项式。

用理想子图法求Pk(G)的步骤：

(1) 画出G的补图Gˉ\bar GGˉ
(2) 求出关于补图的 ri=Ni(Gˉ),(1≤i≤n){r_i} = {N_i}(\bar G),(1 \le i \le n)ri=Ni(Gˉ),(1≤i≤n)
(3) 写出关于补图的伴随多项式$h(\bar G,x) = \sum\limits_{i = 1}^n {{r_i}{x^i}} $
(4) 将xi=[k]i{x^i} = {[k]_i}xi=[k]i代入伴随多项式中得到Pk(G)P_k(G)Pk(G)。

定理3 若G有t个分支H1,H2,…Ht,且Hi的伴随多项式为h (Hi, x), i=1,2,…,t, 则：

h(G,x)=∏i=1th(Hi,x)h(G,x) = \prod\limits_{i = 1}^t {h({H_i},x)} h(G,x)=i=1∏th(Hi,x)

该定理说明，在求Gˉ\bar GGˉ的伴随多项式时，可以分别求出它的每个分支的伴随多项式，然后将它们作乘积。
证明：（未解决）
- 分析：由伴随多项式定义：h(G,x)=∑k=1nNk(G)xkh(G,x) = \sum\limits_{k = 1}^n {{N_k}(G)} {x^k}h(G,x)=k=1∑nNk(G)xk
  所以，我们只需要证明 Nk(G){N_k}(G)Nk(G) 等于 $\prod\limits_{i = 1}^t {h({H_i},x)} $的k次项系数即可。
- 设∣V(G)∣=n\left| {V(G)} \right| = n∣V(G)∣=n ∣V(Hi)∣=ni\left| {V({H_i})} \right| = {n_i}∣V(Hi)∣=ni h(Hi,x)=∑j=1niaijxj,i=1,2,...,th({H_i},x) = \sum\limits_{j = 1}^{{n_i}} {{a_{ij}}} {x^j},i = 1,2,...,th(Hi,x)=j=1∑niaijxj,i=1,2,...,t $\sum\limits_{i = 1}^t {{n_i} = n} $
  - 一方面：$\prod\limits_{i = 1}^t {h({H_i},x)} = \prod\limits_{i = 1}^t {\sum\limits_{j = 1}^{{n_i}} {{a_{ij}}{x^j}} } $该多项式中 xkx^kxk 的系数rk为：
    rk=∑i1+i2+⋯+it=ka1i1a2i2⋯atit{r_k} = \sum\limits_{{i_1} + {i_2} + \cdots + {i_t} = k}^{} {{a_{1{i_1}}}{a_{2{i_2}}} \cdots {a_{t{i_t}}}} rk=i1+i2+⋯+it=k∑a1i1a2i2⋯atit
  - 另一方面：设Mj是Hj中具有ij个分支的Hj的理想子图。当i1+i2+…+it=k时，M1∪ M2 ∪… ∪Mt必是G的具有k个分支的理想子图。在给定的i1,i2,…,it且i1+i2+…+it=k情形下，对应的G的具有k个分支的理想子图个数为：Ni1(H1)Ni2(H2)⋯Nit(Ht){N_{{i_1}}}({H_1}){N_{{i_2}}}({H_2}) \cdots {N_{{i_t}}}({H_t})Ni1(H1)Ni2(H2)⋯Nit(Ht)所以，G的具有k个分支的理想子图的总个数为：Nk(G)=∑i1+i2+⋯it=kNi1(H1)Ni2(H2)⋯Nit(Ht){N_k}(G) = \sum\limits_{{i_1} + {i_2} + \cdots {i_t} = k}^{} {{N_{{i_1}}}({H_1}){N_{{i_2}}}({H_2}) \cdots {N_{{i_t}}}({H_t})} Nk(G)=i1+i2+⋯it=k∑Ni1(H1)Ni2(H2)⋯Nit(Ht)
    =∑i1+i2+⋯+it=ka1i1a2i2⋯atit= \sum\limits_{{i_1} + {i_2} + \cdots + {i_t} = k}^{} {{a_{1{i_1}}}{a_{2{i_2}}} \cdots {a_{t{i_t}}}} =i1+i2+⋯+it=k∑a1i1a2i2⋯atit所以得：h(G,x)=∏i=1th(Hi,x)h(G,x) = \prod\limits_{i = 1}^t {h({H_i},x)} h(G,x)=i=1∏th(Hi,x)

色多项式的性质

定理4 n阶单图G的色多项式Pk(G)是常数项为0的首1整系数多项式，且各项系数符号正负相间。

证明：对边数作数学归纳（借助定理一递推式）

例5 （单图色多项式Pk(G)中kn−1k^{n-1}kn−1的系数是-m）

(1) 用递推公式证明：设G=(n ,m)是单图，则在其色多项式Pk(G)中kn−1k^{n-1}kn−1的系数是-m。
(2) 不存在以k^4-3k3+3k^2为其色多项式的单图。
证明：（1）数学归纳（2）反证
例6 求证：下面图G1与G2非同构但具有相同的色多项式。

小结：

边着色
- 论证关系：
  - 引理 >> 维津定理（数学归纳） >> 定理4， (定理5 >> 定理6)
证明题：
- 反证
- 数学归纳（递推减边，删点等）
- 导出子图局部调整

习题7：

P187—190 习题7 ：1----6 7----9

7.1 求边着色，与顶点着色问题：
- 求边着色：
  - 将图分类
    - 偶图:Δ\DeltaΔ
    - 一般简单图：χ′(G)=Δ或χ′(G)=Δ+1\chi '(G) = \Delta 或 \chi '(G) = \Delta {\rm{ + 1}}χ′(G)=Δ或χ′(G)=Δ+1
    - 特殊简单图：
      - 只有一个最大度或恰有两个相邻的最大度 : Δ\DeltaΔ
      - n=2k+1 且m>kΔm>k\Deltam>kΔ : Δ+1\Delta+1Δ+1
      - 奇数阶正则单图： Δ+1\Delta+1Δ+1
    - 其他：
      - 如果他的所有圈有同样的奇偶性，则χ′(G)=Δ(G)\chi '(G)= \Delta(G)χ′(G)=Δ(G)
      - 若G中恰有一个点的度达到最大n-1,则χ′(G)=Δ(G)=n−1\chi '(G) = \Delta(G) = n-1χ′(G)=Δ(G)=n−1
      - 尝试：如找圈，匹配，因子分解等
      - 彼得森图 χ′(G)=4\chi '(G)=4χ′(G)=4
- 求顶点着色
  - 确定范围：
    - 上界：
      - 一般图： χ≤Δ(G)+1\chi \leq \Delta(G)+1χ≤Δ(G)+1
      - 连通单图，且既不是奇圈又不是完全图： χ≤Δ(G)\chi \leq \Delta(G)χ≤Δ(G)
      - 非空简单图： χ≤Δ2(G)+1\chi \leq \Delta_2(G)+1χ≤Δ2(G)+1
      - 平面图：每个平面图是5可着色的。
    - 下界：
      - 找圈，匹配等
    - 其他：
      - 一个图是可双色当且仅当它没有奇圈
      - G的任意两个奇圈都有一个公共顶点，则 χ≤5\chi ≤5χ≤5。
      - 彼得森图 χ=3\chi = 3χ=3
  - 着色：最大度优先着色
7.2 证明：若G是n阶非空的正则简单图，且n是奇数，则χ′=Δ+1\chi ' = \Delta + 1χ′=Δ+1 。

n=2k+1,m>k∗Δn = 2k+1 , m>k*\Deltan=2k+1,m>k∗Δ
7.3 考虑一个不是奇圈的连通图G,证明:如果他的所有圈有同样的奇偶性，则χ′(G)=Δ(G)\chi '(G)= \Delta(G)χ′(G)=Δ(G)

解：(未解决)
7.4 G为n阶简单图。证明：若G中恰有一个点的度达到最大n-1,则χ′(G)=Δ(G)=n−1\chi '(G) = \Delta(G) = n-1χ′(G)=Δ(G)=n−1

解：设该点为u, G1 = G -u(Δ(G)=n−3\Delta(G)= n-3Δ(G)=n−3)一定可进行n-1着色，u 的邻点有n-1 个
情形1：如果u的邻点着色种类数小于n-1，则u可在n-1种色种选一种不与邻点冲突的着色
情形2：如果u的邻点都着不同的颜色（n-1色）：
作局部调整？：
设H(i,j)为着i色与j色的点导出子图
- 如果H（i，j）中的i与j属于不同分支，则可以交换含i或j所在分支的颜色，使得i,j同色，则转为情形1；
- 如果i,j属于同一分支，(未解决)
7.5 证明Hamilton 3正则图可正常3边着色

H圈为偶圈，可2作色，剩余边为一种色
7.6 证明：一个图是可双色当且仅当它没有奇圈

解：(未解决)
- 必要性：(非B>>非A)存在奇数圈，必然需要至少3着色，则不可双色
- 充分性： (B>>A|| 非A>>非B) 假设G没有奇圈，可以通过深度优先的方式对G进行双着色：
- 给当前点着i色(如果有邻点已经着色，则着与其不同的颜色)，并给下一邻点着j色，不断往下走，如果遇到已经作色的点，则必为偶圈，不会产生冲突。
- 给未着色的点进行上述深度优先的着色，直至所有点都着色
7.7 证明：若G的任意两个奇圈都有一个公共顶点，则 χ≤5\chi ≤5χ≤5。

解：反证
若χ≥6\chi \geq 6χ≥6，且假定在G上已有χ\chiχ种颜色着色。令G1是G
中着1,2,3色的顶点在G中的导出子图，G2是G中着4,5,6色
的顶点在G中的导出子图。显然x(G1)>(G)=3, x(G)2=x-3>=3,
由于二分图的色数均为2,
故G1 G2均不是二分图，所
以在G1,G2中均含有奇圈且它们互不相交。这和假设矛
盾。故x≤5
7.8 证: G为简单图，则 χ≥n2/(n2−2m)\chi \geq n^2/(n^2-2m)χ≥n2/(n2−2m)

7.9 证χ(G−e)=minχ(G,χ(G∗e)\chi(G-e)= min{\chi(G,\chi(G*e)}χ(G−e)=minχ(G,χ(G∗e)
1. (第三次作业 14)证明：若n≥3是G中最长的奇圈的长度，则 (G)≤n+1。
○1 当G的连通分支的点数不大于n+1时，显然可用n+1色着色。
○2 若G中某个连通分支含有n+1阶偶圈，给n+1阶偶圈着n+1色，显然不存在n+1个点之外的点同时与这n+1个点中的相邻两个点邻接，否则会出现n+2阶奇圈。因而与这n+1个点中的相邻的点可取其邻接点邻接的点的颜色。按照这种方式扩张式着色。
○3若G的连通分支不含n+1阶偶圈，可以通过n阶奇圈来构造n+1阶偶圈，在n阶奇圈外增加一个点，与奇圈中相邻两点连接。下证存在这样不会改变最大奇圈的阶数的点。
若不存在这样的点，意味着奇圈的所有边都属于长度至少为n+1阶的偶圈，此时显然存在长度大于n的奇圈，矛盾。
因而证明了构造的合理性，再按照○2的方式进行着色。

第八章拉姆齐问题简介

教学的要求内容之一

独立集与覆盖的性质

定义1 独立 设G=(V ,E)是一个图。V的一个非空顶点子集V1称为G的一个点独立集,如果V1中的顶点互不邻接；G的一个包含顶点数最多的独立集称为G的最大独立集。最大独立集包含的顶点数，称为G的点独立数，记为α(G)。
定义2 覆盖 设G=(V ,E)是一个图。V的一个非空顶点子集K称为G的一个点覆盖,如果E中的每条边至少有一个端点在K中。G的一个包含顶点数最少的点覆盖称为G的最小点覆盖。最小点覆盖包含的顶点数，称为G的点覆盖数，记为β(G)
加莱恒等式

定理1 (加莱) 对任意不含孤立点的n阶图G，有：α(G)+ β(G)= n

证明：一方面，设V1是G的最大点独立集。因为G中每条边的端点最多一个在V1中，所以G中每条边的端点至少有一个在V-V1中。即V-V1构成G的一个点覆盖，于是有：
β(G)≦｜V-V1｜=n - α(G)
另一方面，设K是G的最小点覆盖。因为G中每条边的端点至少有一个在K中，所以G中每条边的端点至多有一个在V-K中。即V-K构成G的一个点独立集，于是有：
α(G) ≥｜V-K｜=n - β(G)
由上面两个不等式，得到：
α(G)+ β(G)= n

边独立集与边覆盖

定义3 边独立 设G=(V ,E)是一个图。E的一个边子集E1称为G的一个边独立集,如果E1中的边互不邻接；G的一个包含边数最多的边独立集称为G的最大边独立集。最大边独立集包含的边数，称为G的边独立数，记为 α‵(G) 。
注：单图的一个边独立集实际上就是图的一个匹配，一个最大边独立集就是其一个最大匹配。
定义4 边覆盖 设G=(V ,E)是一个图。E的一个边子集 L 称为G的一个边覆盖,如果G中的每个顶点均是L中某条边的端点。G的一个包含边数最少的边覆盖称为G的最小边覆盖。最小边覆盖包含的边数，称为G的边覆盖数，记为β‵(G) 。

定理2 (加莱) 对任意不含孤立点的n阶单图G，有：α‵(G)+ β‵(G)= n

证明：一方面, 设α‵(G)= k ,则G的最大匹配由k条边组成，且覆盖了2k个顶点。所以，余下的n-2k个顶点至多需要n-2k条边就可以被覆盖，于是： β‵(G)≦k+(n-2k)=n-k。

从F的每个分支中选取一条边，可作成G的一个匹配，所以α‵(G) ≥ n- β‵(G)。

定理3 设G是无孤立点的偶图，则G中最大点独立集包含的顶点数等于最小边覆盖所包含的边数。

证明：首先由两个加莱恒等式得：α(G)+ β(G)= α‵(G)+ β‵(G) 其次，由第5章中的哥尼定理得： α‵(G)= β(G) 所以得： α(G) = β‵(G) .定理得到证明。

点临界图与边临界图

定义5 设G=(V ,E)是一个图。v是G的一个顶点，e是G的一条边。若 β(G-v) < β(G) ,称v是G的β临界点；若β(G-e) < β(G) ,称e是G的β临界边。

定理4 点v是图G的β临界点当且仅当v含于G的某个最小点覆盖中。

证明

β(G−v)<β(G)\beta (G - v) < \beta (G)β(G−v)<β(G) 即点v是G的一个β临界点。
注：(1) 有β临界边的图必有β临界点。 (2) 有β临界点的图不一定有β临界边。
定义6 临界图 设G=(V ,E)是一个图。若G的每个顶点是G的β临界点，称该图是β 点临界图；若G的每条边均是G的β临界边，称该图是β 边临界图。

拉姆齐数r(m,n)

定义7 拉姆齐数 设m和n是两个正整数，如果存在最小的r(m ,n)阶的图G,使得G中或者有Km或者有n个顶点的独立集，则称正整数r(m, n)为(m, n)拉姆齐数。
如果用定义直接求r(m, n),一般是先恰当找出一个k阶图G1,说明它既不含Km，也不含n点独立集，得到r (m, n)>k;然后再找到一个k+1阶图G2,说明它或者包含Km或者含有n点独立集，得到r(m, n)≦k+1.

定理1 对于任意两个正整数m和n, 且m, n≥2,有：r(m,n)≤r(m,n−1)+r(m−1,n)r(m,n) \le r(m,n - 1) + r(m - 1,n)r(m,n)≤r(m,n−1)+r(m−1,n)并且，如果r (m, n-1)和r (m-1, n)都是偶数，则上面严格不等式成立。

第九章有向图

有向图的概念与性质