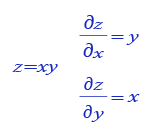前面的课程已经讲解了Python的一些基础操作和使用Notebook实现编程的基础知识，下面通过用Python语言和Numpy库来构建神经网络模型来初步实践。

波士顿房价预测任务

问题描述

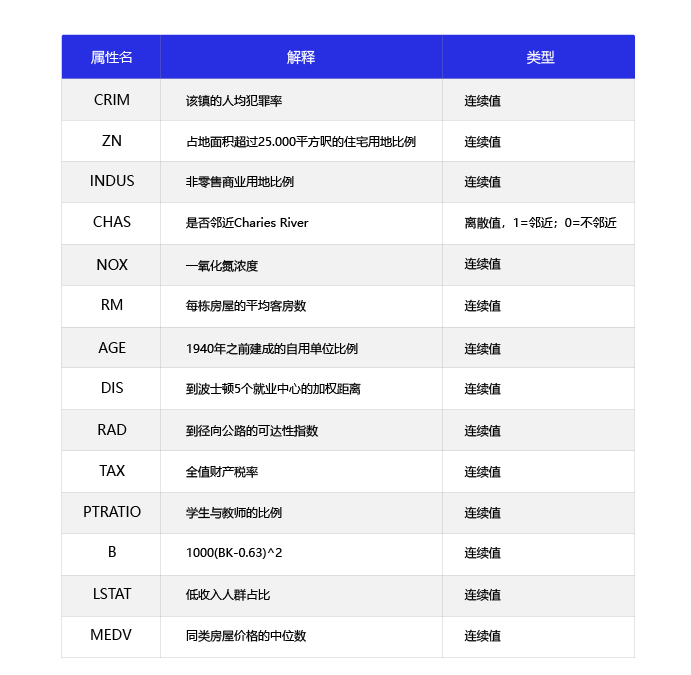
波士顿房价预测是一个经典的机器学习任务，类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同，波士顿地区的房价是由诸多因素影响的。该数据集统计了13种可能影响房价的因素和该类型房屋的均价，期望构建一个基于13个因素进行房价预测的模型，如图1 所示。

图1：波士顿房价影响因素示意图

对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。因为房价是一个连续值，所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题，并用神经网络来实现这个模型。

线性回归模型

假设房价和各影响因素之间能够用线性关系来描述：

y=∑j=1Mxjwj+by = {\sum_{j=1}^Mx_j w_j} + by=j=1∑Mxjwj+b

模型的求解即是通过数据拟合出每个wjw_jwj和bbb。其中，wjw_jwj和bbb分别表示该线性模型的权重和偏置。一维情况下，wjw_jwj 和 bbb 是直线的斜率和截距。

线性回归模型使用均方误差作为损失函数（Loss），用以衡量预测房价和真实房价的差异，公式如下：

MSE=1n∑i=1n(Yi^−Yi)2MSE = \frac{1}{n} \sum_{i=1}^n(\hat{Y_i} - {Y_i})^{2}MSE=n1i=1∑n(Yi^−Yi)2

线性回归模型的神经网络结构

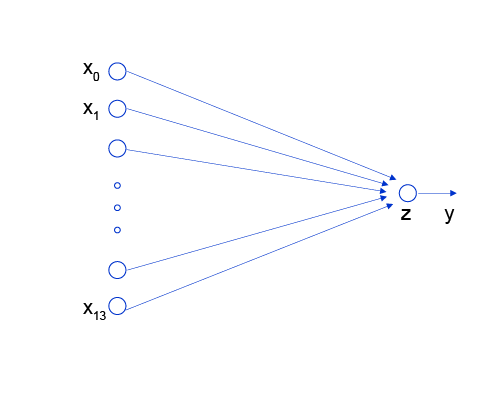
神经网络的标准结构中每个神经元由加权和与非线性变换构成，然后将多个神经元分层的摆放并连接形成神经网络。线性回归模型可以认为是神经网络模型的一种极简特例，是一个只有加权和、没有非线性变换的神经元（无需形成网络），如图2 所示。

图2：线性回归模型的神经网络结构

构建波士顿房价预测任务的神经网络模型

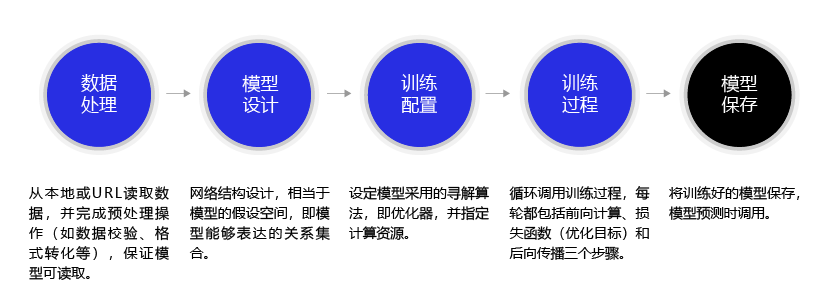
深度学习不仅实现了模型的端到端学习，还推动了人工智能进入工业大生产阶段，产生了标准化、自动化和模块化的通用框架。不同场景的深度学习模型具备一定的通用性，五个步骤即可完成模型的构建和训练，如图3 所示。

图3：构建神经网络/深度学习模型的基本步骤

正是由于深度学习的建模和训练的过程存在通用性，在构建不同的模型时，只有模型三要素不同，其它步骤基本一致，深度学习框架才有用武之地。

注：从本地或URL读取数据的格式不同，在处理数据时需注意格式的转换等问题。

数据处理

数据处理包含五个部分：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后，才能被模型调用。

说明：

本教程中的代码都可以在AIStudio上直接运行，Print结果都是基于程序真实运行的结果。
由于是真实案例，代码之间存在依赖关系，因此需要读者逐条、全部运行，否则会导致命令执行报错。

读入数据

通过如下代码读入数据，了解下波士顿房价的数据集结构，数据存放在本地目录下housing.data文件中。

# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
print(data)
print(type(data))
print(np.size(data))
print(data.shape)
print(data.shape[0])

结果如下：
[6.320e-03 1.800e+01 2.310e+00 … 3.969e+02 7.880e+00 1.190e+01]
<class ‘numpy.ndarray’>
7084
(7084,)
7084
可以看到读入的数据是numpy.ndarray格式

数据形状变换

由于读入的原始数据是1维的，所有数据都连在一起。因此需要我们将数据的形状进行变换，形成一个2维的矩阵，每行为一个数据样本（14个值），每个数据样本包含13个X（影响房价的特征）和一个Y（该类型房屋的均价）。

# 读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推....
# 这里对原始数据做reshape，变成N x 14的形式
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
#data = data.reshape([data.shape[0] // feature_num, feature_num])
data = data.reshape([-1,feature_num])
print(data.shape)

结果为：
(506, 14)

在上述代码中，使用reshape()函数对data进行了形状变换。
函数reshape(a, newshape, order=‘C’)
Gives a new shape to an array without changing its data.

数据集划分

将数据集划分成训练集和测试集，其中训练集用于确定模型的参数，测试集用于评判模型的效果。
在本案例中，我们将80%的数据用作训练集，20%用作测试集，实现代码如下。通过打印训练集的形状，可以发现共有404个样本，每个样本含有13个特征和1个预测值。

ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape

数据归一化处理

对每个特征进行归一化处理，使得每个特征的取值缩放到0~1之间。这样做有两个好处：一是模型训练更高效；二是特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）。

# 计算train数据集的最大值，最小值，平均值
maximums, minimums, avgs = \training_data.max(axis=0), \training_data.min(axis=0), \training_data.sum(axis=0) / training_data.shape[0]
print(maximums, minimums, avgs)
# 对数据进行归一化处理
for i in range(feature_num):print(maximums[i], minimums[i], avgs[i])data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])

注：
函数max(axis=0)表示对每一列的值取最大值,max(axis=1)表示对每一行的值取最大值。

封装成load data函数

将上述几个数据处理操作封装成load data函数，以便下一步模型的调用，实现方法如下。

def load_data():# 从文件导入数据datafile = './work/housing.data'data = np.fromfile(datafile, sep=' ')# 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]feature_num = len(feature_names)# 将原始数据进行Reshape，变成[N, 14]这样的形状data = data.reshape([data.shape[0] // feature_num, feature_num])# 将原数据集拆分成训练集和测试集# 这里使用80%的数据做训练，20%的数据做测试# 测试集和训练集必须是没有交集的ratio = 0.8offset = int(data.shape[0] * ratio)training_data = data[:offset]# 计算训练集的最大值，最小值，平均值maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \training_data.sum(axis=0) / training_data.shape[0]# 对数据进行归一化处理for i in range(feature_num):#print(maximums[i], minimums[i], avgs[i])data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])# 训练集和测试集的划分比例training_data = data[:offset]test_data = data[offset:]return training_data, test_data

加载数据：

# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]

模型设计

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。
将上述计算预测输出的过程以“类和对象”的方式来描述，类成员变量有参数www和bbb。通过写一个forward函数（代表“前向计算”）完成上述从特征和参数到输出预测值的计算过程，代码如下所示。

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，# 此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn z

训练配置

模型设计完成后，需要通过训练配置寻找模型的最优值，即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。

通过模型计算x1x_1x1表示的影响因素所对应的房价应该是zzz, 但实际数据告诉我们房价是yyy。这时我们需要有某种指标来衡量预测值zzz跟真实值yyy之间的差距。对于回归问题，最常采用的衡量方法是使用均方误差作为评价模型好坏的指标，具体定义如下：

Loss=(y−z)2Loss = (y - z)^2Loss=(y−z)2

上式中的LossLossLoss（简记为: LLL）通常也被称作损失函数，它是衡量模型好坏的指标。在回归问题中均方误差是一种比较常见的形式，分类问题中通常会采用交叉熵作为损失函数，在后续的章节中会更详细的介绍。

因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数NNN。
Loss=1N∑i=1N(yi−zi)2Loss= \frac{1}{N}\sum_{i=1}^N{(y_i - z_i)^2}Loss=N1i=1∑N(yi−zi)2
在Network类下面添加损失函数的计算过程如下：

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ycost = error * errorcost = np.mean(cost)return cost

net = Network(num_of_weights)
生成对应数量的权重序列。

训练过程

上述计算过程描述了如何构建神经网络，通过神经网络完成预测值和损失函数的计算。接下来介绍如何求解参数www和bbb的数值，这个过程也称为模型训练过程。训练过程是深度学习模型的关键要素之一，其目标是让定义的损失函数LossLossLoss尽可能的小，也就是说找到一个参数解www和bbb使得损失函数取得极小值。

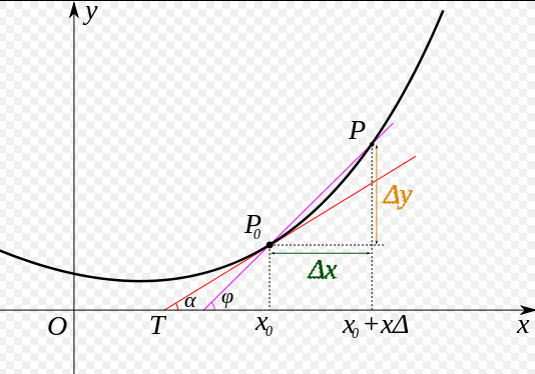
我们先做一个小测试：如图5 所示，基于微积分知识，求一条曲线在某个点的斜率等于函数该点的导数值。那么大家思考下，当处于曲线的极值点时，该点的斜率是多少？

图5：曲线斜率等于导数值

这个问题并不难回答，处于曲线极值点时的斜率为0，即函数在极值点处的导数为0。那么，让损失函数取极小值的www和bbb应该是下述方程组的解：
∂L∂w=0\frac{\partial{L}}{\partial{w}}=0∂w∂L=0
∂L∂b=0\frac{\partial{L}}{\partial{b}}=0∂b∂L=0

将样本数据(x,y)(x, y)(x,y)带入上面的方程组中即可求解出www和bbb的值，但是这种方法只对线性回归这样简单的任务有效。如果模型中含有非线性变换，或者损失函数不是均方差这种简单的形式，则很难通过上式求解。为了解决这个问题，下面我们将引入更加普适的数值求解方法：梯度下降法。

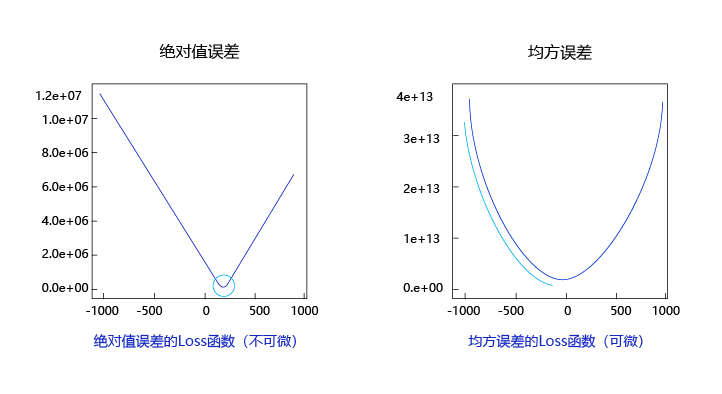
观察上述曲线呈现出“圆滑”的坡度，这正是我们选择以均方误差作为损失函数的原因之一。图6 呈现了只有一个参数维度时，均方误差和绝对值误差（只将每个样本的误差累加，不做平方处理）的损失函数曲线图。

图6：均方误差和绝对值误差损失函数曲线图

由此可见，均方误差表现的“圆滑”的坡度有两个好处：

曲线的最低点是可导的。
越接近最低点，曲线的坡度逐渐放缓，有助于通过当前的梯度来判断接近最低点的程度（是否逐渐减少步长，以免错过最低点）。

而这两个特性绝对值误差是不具备的，这也是损失函数的设计不仅仅要考虑“合理性”，还要追求“易解性”的原因。

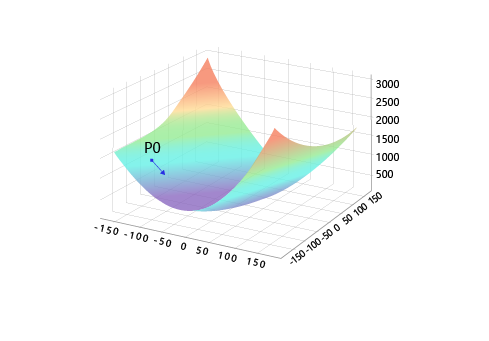
现在我们要找出一组[w5,w9][w_5, w_9][w5,w9]的值，使得损失函数最小，实现梯度下降法的方案如下：

步骤1：随机的选一组初始值，例如：[w5,w9]=[−100.0,−100.0][w_5, w_9] = [-100.0, -100.0][w5,w9]=[−100.0,−100.0]
步骤2：选取下一个点[w5′,w9′][w_5^{'} , w_9^{'}][w5′,w9′]，使得L(w5′,w9′)<L(w5,w9)L(w_5^{'} , w_9^{'}) < L(w_5, w_9)L(w5′,w9′)<L(w5,w9)
步骤3：重复步骤2，直到损失函数几乎不再下降。

如何选择[w5′,w9′][w_5^{'} , w_9^{'}][w5′,w9′]是至关重要的，第一要保证LLL是下降的，第二要使得下降的趋势尽可能的快。微积分的基础知识告诉我们，沿着梯度的反方向，是函数值下降最快的方向，如图7 所示。简单理解，函数在某一个点的梯度方向是曲线斜率最大的方向，但梯度方向是向上的，所以下降最快的是梯度的反方向。

图7：梯度下降方向示意图

计算梯度

上面我们讲过了损失函数的计算方法，这里稍微加以改写。为了梯度计算更加简洁，引入因子12\frac{1}{2}21，定义损失函数如下：

L=12N∑i=1N(yi−zi)2L= \frac{1}{2N}\sum_{i=1}^N{(y_i - z_i)^2}L=2N1i=1∑N(yi−zi)2

其中ziz_izi是网络对第iii个样本的预测值：

zi=∑j=012xij⋅wj+bz_i = \sum_{j=0}^{12}{x_i^{j}\cdot w_j} + bzi=j=0∑12xij⋅wj+b

梯度的定义：

gradient=(∂L∂w0,∂L∂w1,...,∂L∂w12,∂L∂b)gradient= (\frac{\partial{L}}{\partial{w_0}},\frac{\partial{L}}{\partial{w_1}}, ... ,\frac{\partial{L}}{\partial{w_{12}}} ,\frac{\partial{L}}{\partial{b}})gradient=(∂w0∂L,∂w1∂L,...,∂w12∂L,∂b∂L)

可以计算出LLL对www和bbb的偏导数：

∂L∂wj=1N∑i=1N(zi−yi)∂zi∂wj=1N∑i=1N(zi−yi)xij\frac{\partial{L}}{\partial{w_j}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{w_j}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)x_i^{j}}∂wj∂L=N1i=1∑N(zi−yi)∂wj∂zi=N1i=1∑N(zi−yi)xij

∂L∂b=1N∑i=1N(zi−yi)∂zi∂b=1N∑i=1N(zi−yi)\frac{\partial{L}}{\partial{b}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)\frac{\partial{z_i}}{\partial{b}}} = \frac{1}{N}\sum_{i=1}^N{(z_i - y_i)}∂b∂L=N1i=1∑N(zi−yi)∂b∂zi=N1i=1∑N(zi−yi)

从导数的计算过程可以看出，因子12\frac{1}{2}21被消掉了，这是因为二次函数求导的时候会产生因子222，这也是我们将损失函数改写的原因。

下面我们考虑只有一个样本的情况下，计算梯度：

L=12(yi−zi)2L= \frac{1}{2}{(y_i - z_i)^2}L=21(yi−zi)2

z1=x10⋅w0+x11⋅w1+...+x112⋅w12+bz_1 = {x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + bz1=x10⋅w0+x11⋅w1+...+x112⋅w12+b

可以计算出：

L=12(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)2L= \frac{1}{2}{({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)^2}L=21(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)2

可以计算出LLL对www和bbb的偏导数：

∂L∂w0=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅x10=(z1−y1)⋅x10\frac{\partial{L}}{\partial{w_0}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_12} + b - y_1)\cdot x_1^{0}=({z_1} - {y_1})\cdot x_1^{0}∂w0∂L=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅x10=(z1−y1)⋅x10

∂L∂b=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅1=(z1−y1)\frac{\partial{L}}{\partial{b}} = ({x_1^{0}\cdot w_0} + {x_1^{1}\cdot w_1} + ... + {x_1^{12}\cdot w_{12}} + b - y_1)\cdot 1 = ({z_1} - {y_1})∂b∂L=(x10⋅w0+x11⋅w1+...+x112⋅w12+b−y1)⋅1=(z1−y1)

使用Numpy进行梯度计算

基于Numpy广播机制（对向量和矩阵计算如同对1个单一变量计算一样），可以更快速的实现梯度计算。计算梯度的代码中直接用(z1−y1)∗x1(z_1 - y_1) * x_1(z1−y1)∗x1，得到的是一个13维的向量，每个分量分别代表该维度的梯度。

z = net.forward(x)
gradient_w = (z - y) * x
print('gradient_w shape {}'.format(gradient_w.shape))
print(gradient_w)

上面gradient_w的每一行代表了一个样本对梯度的贡献。根据梯度的计算公式，总梯度是对每个样本对梯度贡献的平均值。

我们也可以使用Numpy的均值函数来完成此过程：

# axis = 0 表示把每一行做相加然后再除以总的行数
gradient_w = np.mean(gradient_w, axis=0)
print('gradient_w ', gradient_w.shape)
print('w ', net.w.shape)
print(gradient_w)
print(net.w)

我们使用Numpy的矩阵操作方便地完成了gradient的计算，但引入了一个问题，gradient_w的形状是(13,)，而w的维度是(13, 1)。导致该问题的原因是使用np.mean函数时消除了第0维。为了加减乘除等计算方便，gradient_w和w必须保持一致的形状。因此我们将gradient_w的维度也设置为(13, 1)，代码如下：

gradient_w = gradient_w[:, np.newaxis]      #
print('gradient_w shape', gradient_w.shape)

综合上面的讨论，计算梯度的代码如下所示。

z = net.forward(x)
gradient_w = (z - y) * x
gradient_w = np.mean(gradient_w, axis=0)
gradient_w = gradient_w[:, np.newaxis]

上述代码非常简洁地完成了www的梯度计算。同样，计算bbb的梯度的代码也是类似的原理。

gradient_b = (z - y)
gradient_b = np.mean(gradient_b)
# 此处b是一个数值，所以可以直接用np.mean得到一个标量

将上面计算www和bbb的梯度的过程，写成Network类的gradient函数，实现方法如下所示。

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ynum_samples = error.shape[0]cost = error * errorcost = np.sum(cost) / num_samplesreturn costdef gradient(self, x, y):z = self.forward(x)gradient_w = (z-y)*xgradient_w = np.mean(gradient_w, axis=0)gradient_w = gradient_w[:, np.newaxis]gradient_b = (z - y)gradient_b = np.mean(gradient_b)return gradient_w, gradient_b

在上述代码中，每次更新参数使用的语句：
net.w[5] = net.w[5] - eta * gradient_w5

相减：参数需要向梯度的反方向移动。
eta：控制每次参数值沿着梯度反方向变动的大小，即每次移动的步长，又称为学习率。

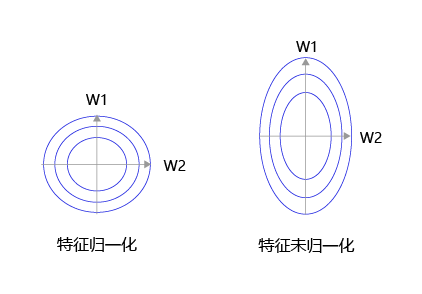
大家可以思考下，为什么之前我们要做输入特征的归一化，保持尺度一致？这是为了让统一的步长更加合适。

如图8 所示，特征输入归一化后，不同参数输出的Loss是一个比较规整的曲线，学习率可以设置成统一的值；特征输入未归一化时，不同特征对应的参数所需的步长不一致，尺度较大的参数需要大步长，尺寸较小的参数需要小步长，导致无法设置统一的学习率。

图8：未归一化的特征，会导致不同特征维度的理想步长不同

代码封装Train函数

将上面的循环计算过程封装在train和update函数中，实现方法如下所示。

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights,1)self.w[5] = -100.self.w[9] = -100.self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ynum_samples = error.shape[0]cost = error * errorcost = np.sum(cost) / num_samplesreturn costdef gradient(self, x, y):z = self.forward(x)gradient_w = (z-y)*xgradient_w = np.mean(gradient_w, axis=0)gradient_w = gradient_w[:, np.newaxis]gradient_b = (z - y)gradient_b = np.mean(gradient_b)        return gradient_w, gradient_bdef update(self, graident_w5, gradient_w9, eta=0.01):net.w[5] = net.w[5] - eta * gradient_w5net.w[9] = net.w[9] - eta * gradient_w9def train(self, x, y, iterations=100, eta=0.01):points = []losses = []for i in range(iterations):points.append([net.w[5][0], net.w[9][0]])z = self.forward(x)L = self.loss(z, y)gradient_w, gradient_b = self.gradient(x, y)gradient_w5 = gradient_w[5][0]gradient_w9 = gradient_w[9][0]self.update(gradient_w5, gradient_w9, eta)losses.append(L)if i % 50 == 0:print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))return points, losses# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=2000
# 启动训练
points, losses = net.train(x, y, iterations=num_iterations, eta=0.01)# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

训练扩展到全部参数

为了能给读者直观的感受，上面演示的梯度下降的过程仅包含w5w_5w5和w9w_9w9两个参数，但房价预测的完整模型，必须要对所有参数www和bbb进行求解。这需要将Network中的update和train函数进行修改。由于不再限定参与计算的参数（所有参数均参与计算），修改之后的代码反而更加简洁。实现逻辑：“前向计算输出、根据输出和真实值计算Loss、基于Loss和输入计算梯度、根据梯度更新参数值”四个部分反复执行，直到到达参数最优点。具体代码如下所示。

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ynum_samples = error.shape[0]cost = error * errorcost = np.sum(cost) / num_samplesreturn costdef gradient(self, x, y):z = self.forward(x)gradient_w = (z-y)*xgradient_w = np.mean(gradient_w, axis=0)gradient_w = gradient_w[:, np.newaxis]gradient_b = (z - y)gradient_b = np.mean(gradient_b)        return gradient_w, gradient_bdef update(self, gradient_w, gradient_b, eta = 0.01):self.w = self.w - eta * gradient_wself.b = self.b - eta * gradient_bdef train(self, x, y, iterations=100, eta=0.01):losses = []for i in range(iterations):z = self.forward(x)L = self.loss(z, y)gradient_w, gradient_b = self.gradient(x, y)self.update(gradient_w, gradient_b, eta)losses.append(L)if (i+1) % 10 == 0:print('iter {}, loss {}'.format(i, L))return losses# 获取数据
train_data, test_data = load_data()
x = train_data[:, :-1]
y = train_data[:, -1:]
# 创建网络
net = Network(13)
num_iterations=1000
# 启动训练
losses = net.train(x,y, iterations=num_iterations, eta=0.01)# 画出损失函数的变化趋势
plot_x = np.arange(num_iterations)
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

随机梯度下降法（ Stochastic Gradient Descent）

在上述程序中，每次损失函数和梯度计算都是基于数据集中的全量数据。对于波士顿房价预测任务数据集而言，样本数比较少，只有404个。但在实际问题中，数据集往往非常大，如果每次都使用全量数据进行计算，效率非常低，通俗地说就是“杀鸡焉用牛刀”。由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（Stochastic Gradient Descent，SGD），核心概念如下：

min-batch：每次迭代时抽取出来的一批数据被称为一个min-batch。
batch_size：一个mini-batch所包含的样本数目称为batch_size。
epoch：当程序迭代的时候，按mini-batch逐渐抽取出样本，当把整个数据集都遍历到了的时候，则完成了一轮训练，也叫一个epoch。启动训练时，可以将训练的轮数num_epochs和batch_size作为参数传入。

下面结合程序介绍具体的实现过程，涉及到数据处理和训练过程两部分代码的修改。

数据处理代码修改

数据处理需要实现拆分数据批次和样本乱序（为了实现随机抽样的效果）两个功能。

# 获取数据
train_data, test_data = load_data()# 打乱样本顺序
np.random.shuffle(train_data)# 将train_data分成多个mini_batch
batch_size = 10
n = len(train_data)
mini_batches = [train_data[k:k+batch_size] for k in range(0, n, batch_size)]
#生成不同的batch# 创建网络
net = Network(13)# 依次使用每个mini_batch的数据
for mini_batch in mini_batches:x = mini_batch[:, :-1]y = mini_batch[:, -1:]loss = net.train(x, y, iterations=1)

训练过程代码修改

将每个随机抽取的mini-batch数据输入到模型中用于参数训练。训练过程的核心是两层循环：

第一层循环，代表样本集合要被训练遍历几次，称为“epoch”，代码如下：

for epoch_id in range(num_epoches):

第二层循环，代表每次遍历时，样本集合被拆分成的多个批次，需要全部执行训练，称为“iter (iteration)”，代码如下：

for iter_id,mini_batch in emumerate(mini_batches):

在两层循环的内部是经典的四步训练流程：前向计算->计算损失->计算梯度->更新参数，这与大家之前所学是一致的，代码如下：

            x = mini_batch[:, :-1]y = mini_batch[:, -1:]a = self.forward(x)  #前向计算loss = self.loss(a, y)  #计算损失gradient_w, gradient_b = self.gradient(x, y)  #计算梯度self.update(gradient_w, gradient_b, eta)  #更新参数

将两部分改写的代码集成到Network类中的train函数中，最终的实现如下。

import numpy as npclass Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子#np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ynum_samples = error.shape[0]cost = error * errorcost = np.sum(cost) / num_samplesreturn costdef gradient(self, x, y):z = self.forward(x)N = x.shape[0]gradient_w = 1. / N * np.sum((z-y) * x, axis=0)gradient_w = gradient_w[:, np.newaxis]gradient_b = 1. / N * np.sum(z-y)return gradient_w, gradient_bdef update(self, gradient_w, gradient_b, eta = 0.01):self.w = self.w - eta * gradient_wself.b = self.b - eta * gradient_bdef train(self, training_data, num_epoches, batch_size=10, eta=0.01):n = len(training_data)losses = []for epoch_id in range(num_epoches):# 在每轮迭代开始之前，将训练数据的顺序随机打乱# 然后再按每次取batch_size条数据的方式取出np.random.shuffle(training_data)# 将训练数据进行拆分，每个mini_batch包含batch_size条的数据mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]for iter_id, mini_batch in enumerate(mini_batches):#print(self.w.shape)#print(self.b)x = mini_batch[:, :-1]y = mini_batch[:, -1:]a = self.forward(x)loss = self.loss(a, y)gradient_w, gradient_b = self.gradient(x, y)self.update(gradient_w, gradient_b, eta)losses.append(loss)print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.format(epoch_id, iter_id, loss))return losses# 获取数据
train_data, test_data = load_data()# 创建网络
net = Network(13)
# 启动训练
losses = net.train(train_data, num_epoches=50, batch_size=100, eta=0.1)# 画出损失函数的变化趋势
plot_x = np.arange(len(losses))
plot_y = np.array(losses)
plt.plot(plot_x, plot_y)
plt.show()

观察上述Loss的变化，随机梯度下降加快了训练过程，但由于每次仅基于少量样本更新参数和计算损失，所以损失下降曲线会出现震荡。

说明：

由于房价预测的数据量过少，所以难以感受到随机梯度下降带来的性能提升。

总结

本节我们详细介绍了如何使用Numpy实现梯度下降算法，构建并训练了一个简单的线性模型实现波士顿房价预测，可以总结出，使用神经网络建模房价预测有三个要点：

构建网络，初始化参数w和b，定义预测和损失函数的计算方法。
随机选择初始点，建立梯度的计算方法和参数更新方式。
从总的数据集中抽取部分数据作为一个mini_batch，计算梯度并更新参数，不断迭代直到损失函数几乎不再下降。

作业1-4

基本知识

1. 求导的链式法则

链式法则是微积分中的求导法则，用于求一个复合函数的导数，是在微积分的求导运算中一种常用的方法。复合函数的导数将是构成复合这有限个函数在相应点的导数的乘积，就像锁链一样一环套一环，故称链式法则。如图9 所示，如果求最终输出对内层输入（第一层）的梯度，等于外层梯度（第二层）乘以本层函数的梯度。

图9：求导的链式法则

2. 计算图的概念

（1）为何是反向计算梯度？即梯度是由网络后端向前端计算。当前层的梯度要依据处于网络中后一层的梯度来计算，所以只有先算后一层的梯度才能计算本层的梯度。

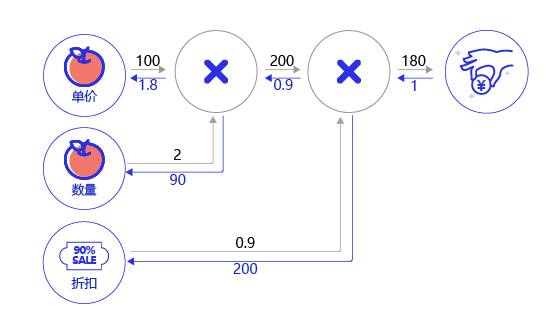
（2）案例：购买苹果产生消费的计算图。假设一家商店9折促销苹果，每个的单价100元。计算一个顾客总消费的结构如 图10 所示。

图10：购买苹果所产生的消费计算图

前向计算过程：以黑色箭头表示，顾客购买了2个苹果，再加上九折的折扣，一共消费100*2*0.9=180元。
后向传播过程：以红色箭头表示，根据链式法则，本层的梯度计算 * 后一层传递过来的梯度，所以需从后向前计算。

最后一层的输出对自身的求导为1。导数第二层根据 图11 所示的乘法求导的公式，分别为0.9*1和200*1。同样的，第三层为100 * 0.9=90，2 * 0.9=1.8。

图11：乘法求导的公式

注：
上图中，假设苹果单价为xxx，数量为yyy，折扣为zzz，苹果总价为f1f_1f1，实付金额为f2f_2f2，则：
f1=xyf_1=xyf1=xyf2=f1zf_2 = f_1zf2=f1z
有：
∂f2∂z=f1\frac{\partial{f_2}}{\partial{z}}=f_1∂z∂f2=f1
∂f2∂x=∂f2∂f1∂f1∂x=zy\begin{aligned} \frac{\partial{f_2}}{\partial{x}}&=\frac{\partial{f_2}}{\partial{f_1}}\frac{\partial{f_1}}{\partial{x}}\\&=zy \end{aligned}∂x∂f2=∂f1∂f2∂x∂f1=zy
∂f2∂y=∂f2∂f1∂f1∂y=zx\begin{aligned} \frac{\partial{f_2}}{\partial{y}}&=\frac{\partial{f_2}}{\partial{f_1}}\frac{\partial{f_1}}{\partial{y}}\\&=zx \end{aligned}∂y∂f2=∂f1∂f2∂y∂f1=zx
图中后向传播所得数值则为对应梯度值。

PaddlePaddle入门|百度零基础实践深度学习课程笔记——使用Python语言和Numpy库来构建神经网络模型相关推荐

2.7mnist手写数字识别之训练调试与优化精讲(百度架构师手把手带你零基础实践深度学习原版笔记系列)
2.7mnist手写数字识别之训练调试与优化精讲(百度架构师手把手带你零基础实践深度学习原版笔记系列) 目录 2.7mnist手写数字识别之训练调试与优化精讲(百度架构师手把手带你零基础实践深度学习原 ...
3.1 计算机视觉的发展和卷积神经网络概要(百度架构师手把手带你零基础实践深度学习原版笔记系列)
3.1 计算机视觉的发展和卷积神经网络(百度架构师手把手带你零基础实践深度学习原版笔记系列) 概要计算机视觉作为一门让机器学会如何去"看"的科学学科,具体的说,就是让机器去识别摄 ...
1.1机器学习和深度学习综述(百度架构师手把手带你零基础实践深度学习原版笔记系列)
人工智能.机器学习.深度学习的关系近些年人工智能.机器学习和深度学习的概念十分火热,但很多从业者却很难说清它们之间的关系,外行人更是雾里看花.在研究深度学习之前,我们先从三个概念的正本清源开始. 概 ...
百度飞桨PaddelePaddle-21天零基础实践深度学习-【手写数字任务】2
百度飞桨PaddelePaddle-21天零基础实践深度学习-[手写数字任务]2 模型设计网络结构损失函数训练配置优化算法模型设计网络结构全连接神经网络经典的全连接神经网络来包含四层网 ...
飞浆PaddlePaddle-百度架构师手把手带你零基础实践深度学习（学习笔记）
飞浆PaddlePaddle-百度架构师手把手带你零基础实践深度学习(学习笔记) 百度架构师手把手带你零基础实践深度学习(打卡学习笔记) 为什么学习飞浆PaddlePaddle,不得不说百度最近几年在 ...
飞桨PaddlePaddle-百度架构师手把手带你零基础实践深度学习——21日学习总结
飞桨PaddlePaddle-百度架构师手把手带你零基础实践深度学习--21日学习总结写在前面的话纯新手小白,第一次接触深度学习方面的应用.感谢飞桨提供的这次学习机会.之前有学习到深度学习的理论方 ...
零基础实践深度学习之数学基础
零基础实践深度学习之数学基础深度学习常用数学知识数学基础知识高等数学线性代数行列式矩阵向量线性方程组矩阵的特征值和特征向量二次型概率论和数理统计随机事件和概率随机变量及其概率 ...
零基础实践深度学习之Python基础
零基础实践深度学习之Python基础 Python数据结构数字字符串列表元组字典 Python面向对象 Python JSON Python异常处理 Python文件操作常见Linux命令 ...
Deeplearning.ai深度学习课程笔记-在线版
注意:请点击阅读原文课程概述课程视频离线版本可以到github:https://github.com/fengdu78/deeplearning_ai_books 查找下载. 课程地址:https ...

PaddlePaddle入门|百度零基础实践深度学习课程笔记——使用Python语言和Numpy库来构建神经网络模型