十六、朴素贝叶斯

作者：Chris Albon

译者：飞龙

协议：CC BY-NC-SA 4.0

伯努利朴素贝叶斯

伯努利朴素贝叶斯分类器假设我们的所有特征都是二元的，它们仅有两个值（例如，已经是独热编码的标称分类特征）。

# 加载库
import numpy as np
from sklearn.naive_bayes import BernoulliNB# 创建三个二元特征
X = np.random.randint(2, size=(100, 3))# 创建二元目标向量
y = np.random.randint(2, size=(100, 1)).ravel()# 查看前十个观测
X[0:10]'''
array([[1, 1, 1],[0, 1, 0],[1, 1, 1],[0, 0, 0],[1, 0, 1],[1, 1, 1],[0, 1, 1],[1, 1, 1],[1, 1, 1],[1, 1, 0]])
'''# 创建伯努利朴素贝叶斯对象，带有每个类别的先验概率
clf = BernoulliNB(class_prior=[0.25, 0.5])# 训练模型
model = clf.fit(X, y)

校准预测概率

类别概率是机器学习模型中常见且有用的部分。在 scikit-learn 中，大多数学习算法允许我们使用predict_proba来查看成员的类别预测概率。例如，如果我们想要仅预测某个类，如果模型预测它们是该类的概率超过 90%，则这非常有用。然而，一些模型，包括朴素贝叶斯分类器输出的概率，不基于现实世界。也就是说，predict_proba可能预测，观测有 0.70 的机会成为某一类，而实际情况是它是 0.10 或 0.99。特别是在朴素贝叶斯中，虽然不同目标类别的预测概率的排名是有效的，但是原始预测概率倾向于接近 0 和 1 的极值。

为了获得有意义的预测概率，我们需要进行所谓的校准。在 scikit-learn 中，我们可以使用CalibratedClassifierCV类，使用 k-fold 交叉验证创建校准良好的预测概率。在CalibratedClassifierCV中，训练集用于训练模型，测试集用于校准预测概率。返回的预测概率是 k 折的平均值。

# 加载库
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
from sklearn.calibration import CalibratedClassifierCV# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target# 创建高斯朴素贝叶斯对象
clf = GaussianNB()# 使用 sigmoid 校准创建校准的交叉验证
clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method='sigmoid')# 校准概率
clf_sigmoid.fit(X, y)'''
CalibratedClassifierCV(base_estimator=GaussianNB(priors=None), cv=2,method='sigmoid')
'''# 创建新的观测
new_observation = [[ 2.6,  2.6,  2.6,  0.4]]# 查看校准概率
clf_sigmoid.predict_proba(new_observation)# array([[ 0.31859969,  0.63663466,  0.04476565]])

高斯朴素贝叶斯分类器

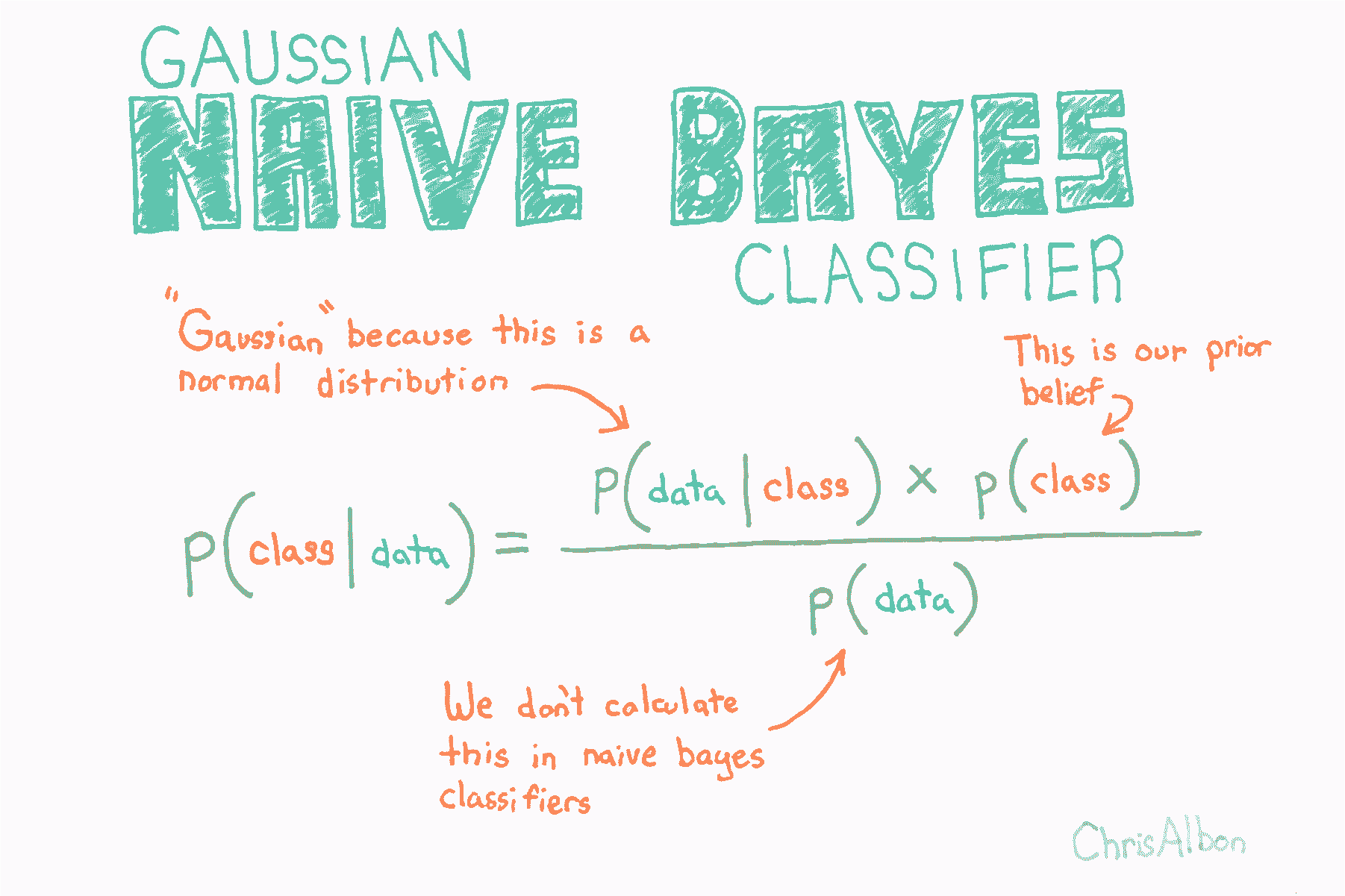
由于正态分布的假设，高斯朴素贝叶斯最适用于我们所有特征都是连续的情况。

# 加载库
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target# 创建高斯朴素贝叶斯对象，带有每个类别的先验概率
clf = GaussianNB(priors=[0.25, 0.25, 0.5])# 训练模型
model = clf.fit(X, y)# 创建新的观测
new_observation = [[ 4,  4,  4,  0.4]]# 预测类别
model.predict(new_observation)# array([1])

注意：来自高斯朴素贝叶斯的原始预测概率（使用predict_proba输出）未校准。也就是说，他们不应该是可信的。如果我们想要创建有用的预测概率，我们将需要使用等渗回归或相关方法来校准它们。

多项式逻辑回归

在多项逻辑回归（MLR）中，我们在 Recipe 15.1 中看到的逻辑函数被 softmax 函数替换：

P(yi=k∣X)=eβkxi∑j=1KeβjxiP(y_i=k \mid X)={\frac {e^{\beta_{k}x_{i}}}{{\sum_{j=1}^{K}}e^{\beta_{j}x_{i}}}}P(yi=k∣X)=∑j=1Keβjxieβkxi

其中 P(yi=k∣X)P(y_i=k \mid X)P(yi=k∣X) 是第 iii 个观测的目标值 yiy_iyi 是类 kkk 的概率，KKK 是类的总数。MLR 的一个实际优点是使用predict_proba方法预测的概率更可靠（即校准更好）。

# 加载库
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target# 标准化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)# 创建 OVR 逻辑回归对象
clf = LogisticRegression(random_state=0, multi_class='multinomial', solver='newton-cg')# 训练模型
model = clf.fit(X_std, y)# 创建新的观测
new_observation = [[.5, .5, .5, .5]]# 预测类别
model.predict(new_observation)# array([1]) # 查看预测概率
model.predict_proba(new_observation)# array([[ 0.01944996,  0.74469584,  0.2358542 ]])

多项式朴素贝叶斯分类器

多项式朴素贝叶斯的工作方式类似于高斯朴素贝叶斯，但假设这些特征是多项式分布的。在实践中，这意味着当我们具有离散数据（例如，电影评级范围为 1 到 5）时，通常使用该分类器。

# 加载库
import numpy as np
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer# 创建文本
text_data = np.array(['I love Brazil. Brazil!','Brazil is best','Germany beats both'])# 创建词袋
count = CountVectorizer()
bag_of_words = count.fit_transform(text_data)# 创建特征矩阵
X = bag_of_words.toarray()# 创建目标向量
y = np.array([0,0,1])# 创建多项式朴素贝叶斯对象，带有每个类别的先验概率
clf = MultinomialNB(class_prior=[0.25, 0.5])# 训练模型
model = clf.fit(X, y)# 创建新的观测
new_observation = [[0, 0, 0, 1, 0, 1, 0]]# 预测新观测的类别
model.predict(new_observation)# array([0])

从零编写朴素贝叶斯分类器

朴素贝叶斯是一种简单的分类器，当只有少量观测可用时，这种分类器表现良好。在本教程中，我们将从头开始创建一个高斯朴素贝叶斯分类器，并使用它来预测以前未见过的数据点的类别。本教程基于 Wikipedia 的朴素贝叶斯分类器页面上的示例，我已经用 Python 实现了它并调整了一些符号来改进解释。

import pandas as pd
import numpy as np

我们的数据集包含八个个体的数据。我们将使用数据集构建一个分类器，该分类器接收个体的身高，体重和脚码，并输出其性别预测。

# 创建空数据帧
data = pd.DataFrame()# 创建我们的目标变量
data['Gender'] = ['male','male','male','male','female','female','female','female']# 创建我们的特征变量
data['Height'] = [6,5.92,5.58,5.92,5,5.5,5.42,5.75]
data['Weight'] = [180,190,170,165,100,150,130,150]
data['Foot_Size'] = [12,11,12,10,6,8,7,9]# 查看数据
data

	Gender	Height	Weight	Foot_Size
0	male	6.00	180	12
1	male	5.92	190	11
2	male	5.58	170	12
3	male	5.92	165	10
4	female	5.00	100	6
5	female	5.50	150	8
6	female	5.42	130	7
7	female	5.75	150	9

上面的数据集用于构造我们的分类器。下面我们将创建一个新的个体，我们知道它的特征值，但不知道它的性别。我们的目标是预测它的性别。

# 创建空数据帧
person = pd.DataFrame()# 为这一行创建相同特征值
person['Height'] = [6]
person['Weight'] = [130]
person['Foot_Size'] = [8]# 查看数据
person

	Height	Weight	Foot_Size
0	6	130	8

贝叶斯定理是一个着名的方程，它允许我们根据数据进行预测。这是贝叶斯定理的经典版本：

P(A∣B)=P(B∣A) P(A)P(B)\displaystyle P(A\mid B)={\frac {P(B\mid A)\,P(A)}{P(B)}}P(A∣B)=P(B)P(B∣A)P(A)

这可能过于抽象，所以让我们替换一些变量以使其更具体。在贝叶斯分类器中，给定数据的情况下，我们有兴趣找出观测的类别（例如男性或女性，垃圾邮件或非垃圾邮件）：

p(class∣data)=p(data∣class)∗p(class)p(data)p(\text{class} \mid \mathbf {\text{data}} )={\frac {p(\mathbf {\text{data}} \mid \text{class}) * p(\text{class})}{p(\mathbf {\text{data}} )}}p(class∣data)=p(data)p(data∣class)∗p(class)

其中：

class\text{class}class 是特定类别（例如男性）
data\mathbf {\text{data}}data 是观测的数据
p(class∣data)p(\text{class} \mid \mathbf {\text{data}} )p(class∣data) 称为后验
p(data|class)p(\text{data|class})p(data|class) 叫做似然
p(class)p(\text{class})p(class) 叫做先验
p(data)p(\mathbf {\text{data}} )p(data) 叫做边缘概率

在贝叶斯分类器中，我们计算每个观测的每个类的后验（严格来说，我们只计算后验的分子，但现在忽略它）。然后，基于后验值最大的类别对观测分类。在我们的例子中，我们为观测预测两个可能的类别（例如男性和女性），因此我们将计算两个后验：一个用于男性，一个用于女性。

p(person is male∣person’s data)=p(person’s data∣person is male)∗p(person is male)p(person’s data)p(\text{person is male} \mid \mathbf {\text{person’s data}} )={\frac {p(\mathbf {\text{person’s data}} \mid \text{person is male}) * p(\text{person is male})}{p(\mathbf {\text{person’s data}} )}}p(person is male∣person’s data)=p(person’s data)p(person’s data∣person is male)∗p(person is male)

p(person is female∣person’s data)=p(person’s data∣person is female)∗p(person is female)p(person’s data)p(\text{person is female} \mid \mathbf {\text{person’s data}} )={\frac {p(\mathbf {\text{person’s data}} \mid \text{person is female}) * p(\text{person is female})}{p(\mathbf {\text{person’s data}} )}}p(person is female∣person’s data)=p(person’s data)p(person’s data∣person is female)∗p(person is female)

高斯朴素的贝叶斯可能是最受欢迎的贝叶斯分类器。为了解释这个名称的含义，让我们看一下当我们应用两个类别（男性和女性）和三个特征变量（高度，重量和尺寸）时贝叶斯方程式的样子：

posterior (male)=P(male) p(height∣male) p(weight∣male) p(foot size∣male)marginal probability{\displaystyle {\text{posterior (male)}}={\frac {P({\text{male}})\,p({\text{height}}\mid{\text{male}})\,p({\text{weight}}\mid{\text{male}})\,p({\text{foot size}}\mid{\text{male}})}{\text{marginal probability}}}}posterior (male)=marginal probabilityP(male)p(height∣male)p(weight∣male)p(foot size∣male)

posterior (female)=P(female) p(height∣female) p(weight∣female) p(foot size∣female)marginal probability{\displaystyle {\text{posterior (female)}}={\frac {P({\text{female}})\,p({\text{height}}\mid{\text{female}})\,p({\text{weight}}\mid{\text{female}})\,p({\text{foot size}}\mid{\text{female}})}{\text{marginal probability}}}}posterior (female)=marginal probabilityP(female)p(height∣female)p(weight∣female)p(foot size∣female)

现在让我们解释一下上面的方程式：

P(male)P({\text{male}})P(male) 是先验概率。正如您所看到的，只是观测是男性的概率。这只是数据集中的男性数量除以数据集中的总人数。
p(height∣female) p(weight∣female) p(foot size∣female)p({\text{height}}\mid{\text{female}})\,p({\text{weight}}\mid{\text{female}})\,p({\text{foot size}}\mid{\text{female}})p(height∣female)p(weight∣female)p(foot size∣female) 是似然。注意我们已经解释了 person’s data\mathbf {\text{person’s data}}person’s data 所以它现在是数据集中的每个特征。“高斯”和“朴素”来自似然中的两个假设：
1. 如果你查看似然中的每项，你会注意到，我们假设每个特征彼此不相关。也就是说，脚码与体重或身高等无关。这显然不是真的，而且是一个“朴素”的假设 - 因此称为“朴素贝叶斯”。
2. 其次，我们假设特征的值（例如女性的身体，女性的体重）通常是高斯分布的。这意味着 p(height∣female)p(\text{height}\mid\text{female})p(height∣female) 是通过将所需参数输入正态分布的概率密度函数来计算的：

p(height∣female)=12πvariance of female height in the data e−(observation’s height−average height of females in the data)22variance of female height in the datap(\text{height}\mid\text{female})=\frac{1}{\sqrt{2\pi\text{variance of female height in the data}}}\,e^{ -\frac{(\text{observation’s height}-\text{average height of females in the data})^2}{2\text{variance of female height in the data}} }p(height∣female)=2πvariance of female height in the data1e−2variance of female height in the data(observation’s height−average height of females in the data)2

marginal probability\text{marginal probability}marginal probability 可能是贝叶斯方法中最令人困惑的部分之一。在玩具示例（包括我们的）中，完全可以计算边际概率。但是，在许多实际情况中，要找到边际概率的值极其困难或不可能（解释为什么超出了本教程的范围）。对于我们的分类器来说，这并不像您想象的那么严重。为什么？因为我们不关心真正的后验值是什么，我们只关心哪个类具有最高的后验值。并且因为边际概率对于所有类别都是相同的，（1）我们可以忽略分母，（2）只计算每个类的后验分子，（3）选择最大的分子。也就是说，我们可以忽略后验分母，并仅根据后验分子的相对值进行预测。

好的！理论结束。现在让我们开始计算贝叶斯方程的所有不同部分。

先验可以是常数或概率分布。在我们的例子中，这只是性别的概率。计算这很简单：

# 男性数量
n_male = data['Gender'][data['Gender'] == 'male'].count()# 女性数量
n_female = data['Gender'][data['Gender'] == 'female'].count()# 总行数
total_ppl = data['Gender'].count()# 男性比例
P_male = n_male/total_ppl# 女性比例
P_female = n_female/total_ppl

请记住，我们的似然中的每一项（例如 p(height∣female)p(\text{height}\mid\text{female})p(height∣female)）都可以看做正态的 PDF。例如：

这意味着对于每个类别（例如女性）和特征（例如身高）组合，我们需要从数据计算方差和均值。Pandas 让这很容易：

# 按性别分组数据，并计算每个特征的均值
data_means = data.groupby('Gender').mean()# 查看值
data_means

	Height	Weight	Foot_Size
Gender
female	5.4175	132.50	7.50
male	5.8550	176.25	11.25

# 按性别分组数据，并计算每个特征的方差
data_variance = data.groupby('Gender').var()# 查看值
data_variance

	Height	Weight	Foot_Size
Gender
female	0.097225	558.333333	1.666667
male	0.035033	122.916667	0.916667

现在我们可以创建我们需要的所有变量。下面的代码可能看起来很复杂，但我们所做的，只是从上面两个表中的每个单元格中创建一个变量。

# 男性的均值
male_height_mean = data_means['Height'][data_variance.index == 'male'].values[0]
male_weight_mean = data_means['Weight'][data_variance.index == 'male'].values[0]
male_footsize_mean = data_means['Foot_Size'][data_variance.index == 'male'].values[0]# 男性的方差
male_height_variance = data_variance['Height'][data_variance.index == 'male'].values[0]
male_weight_variance = data_variance['Weight'][data_variance.index == 'male'].values[0]
male_footsize_variance = data_variance['Foot_Size'][data_variance.index == 'male'].values[0]# Means for female
female_height_mean = data_means['Height'][data_variance.index == 'female'].values[0]
female_weight_mean = data_means['Weight'][data_variance.index == 'female'].values[0]
female_footsize_mean = data_means['Foot_Size'][data_variance.index == 'female'].values[0]# Variance for female
female_height_variance = data_variance['Height'][data_variance.index == 'female'].values[0]
female_weight_variance = data_variance['Weight'][data_variance.index == 'female'].values[0]
female_footsize_variance = data_variance['Foot_Size'][data_variance.index == 'female'].values[0]

最后，我们需要创建一个函数来计算每个似然项的概率密度（例如 p(height∣female)p(\text{height}\mid\text{female})p(height∣female)）。

# 创建计算 p(x | y) 的函数
def p_x_given_y(x, mean_y, variance_y):# 将参数输入到概率密度函数p = 1/(np.sqrt(2*np.pi*variance_y)) * np.exp((-(x-mean_y)**2)/(2*variance_y))# 返回 preturn p

好的！我们的贝叶斯分类器准备就绪。请记住，既然我们可以忽略边际概率（分母），我们实际计算的是：

numerator of the posterior=P(female) p(height∣female) p(weight∣female) p(foot size∣female){\displaystyle {\text{numerator of the posterior}}={P({\text{female}})\,p({\text{height}}\mid{\text{female}})\,p({\text{weight}}\mid{\text{female}})\,p({\text{foot size}}\mid{\text{female}})}{}}numerator of the posterior=P(female)p(height∣female)p(weight∣female)p(foot size∣female)

为此，我们只需要插入未分类个体（height = 6）的值，数据集的变量（例如女性身高的均值）和我们上面编写的函数（p_x_given_y）：

# 如果未分类的观测是男性的后验分子
P_male * \
p_x_given_y(person['Height'][0], male_height_mean, male_height_variance) * \
p_x_given_y(person['Weight'][0], male_weight_mean, male_weight_variance) * \
p_x_given_y(person['Foot_Size'][0], male_footsize_mean, male_footsize_variance)# 6.1970718438780782e-09

# 如果未分类的观测是女性的后验分子
P_female * \
p_x_given_y(person['Height'][0], female_height_mean, female_height_variance) * \
p_x_given_y(person['Weight'][0], female_weight_mean, female_weight_variance) * \
p_x_given_y(person['Foot_Size'][0], female_footsize_mean, female_footsize_variance)# 0.00053779091836300176

因为女性的后验分子大于男性，所以我们预测这个人是女性。

数据科学和人工智能技术笔记十六、朴素贝叶斯相关推荐

数据科学和人工智能技术笔记十二、逻辑回归
十二.逻辑回归作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 C 超参数快速调优有时,学习算法的特征使我们能够比蛮力或随机模型搜索方法更快地搜索最佳超参数. sci ...
数据科学和人工智能技术笔记十五、支持向量机
十五.支持向量机作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 校准 SVC 中的预测概率 SVC 使用超平面来创建决策区域,不会自然输出观察是某一类成员的概率估计. ...
数据科学和人工智能技术笔记十、模型选择
十.模型选择作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 在模型选择期间寻找最佳预处理步骤在进行模型选择时,我们必须小心正确处理预处理. 首先,GridSearc ...
数据科学和人工智能技术笔记十四、K 最近邻
十四.K 最近邻作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 确定 K 的最佳值 # 加载库 from sklearn.neighbors import KNeig ...
数据科学和人工智能技术笔记十九、数据整理（上）
十九.数据整理(上) 作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 在 Pandas 中通过分组应用函数 import pandas as pd# 创建示例数据帧 d ...
数据科学和人工智能技术笔记十三、树和森林
十三.树和森林作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 Adaboost 分类器 # 加载库 from sklearn.ensemble import AdaB ...
数据科学和人工智能技术笔记七、特征工程
七.特征工程作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 稀疏特征矩阵上的降维 # 加载库 from sklearn.preprocessing import St ...
数据科学和人工智能技术笔记六、日期时间预处理
六.日期时间预处理作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 把日期和时间拆成多个特征 # 加载库 import pandas as pd# 创建数据帧 df = ...
数据科学和人工智能技术笔记二十一、统计学
二十一.统计学作者:Chris Albon 译者:飞龙协议:CC BY-NC-SA 4.0 贝塞尔校正贝塞尔的校正是我们在样本方差和样本标准差的计算中使用 n−1n-1n−1 而不是 nnn 的 ...

数据科学和人工智能技术笔记十六、朴素贝叶斯

十六、朴素贝叶斯

伯努利朴素贝叶斯

校准预测概率

高斯朴素贝叶斯分类器

多项式逻辑回归

多项式朴素贝叶斯分类器

从零编写朴素贝叶斯分类器

数据科学和人工智能技术笔记十六、朴素贝叶斯相关推荐

最新文章

热门文章

数据科学和人工智能技术笔记 十六、朴素贝叶斯

十六、朴素贝叶斯

伯努利朴素贝叶斯

校准预测概率

高斯朴素贝叶斯分类器

多项式逻辑回归

多项式朴素贝叶斯分类器

从零编写朴素贝叶斯分类器

数据科学和人工智能技术笔记 十六、朴素贝叶斯相关推荐

最新文章

热门文章

数据科学和人工智能技术笔记十六、朴素贝叶斯

数据科学和人工智能技术笔记十六、朴素贝叶斯相关推荐