RNN 入门教程 Part 3 – 介绍 BPTT 算法和梯度消失问题
转载 - Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients
本文是 RNN入门教程 的第三部分.
In the previous part of the tutorial we implemented a RNN from scratch, but didn’t go into detail on how Backpropagation Through Time (BPTT) algorithms calculates the gradients. In this part we’ll give a brief overview of BPTT and explain how it differs from traditional backpropagation. We will then try to understand the vanishing gradient problem, which has led to the development of LSTMs and GRUs, two of the currently most popular and powerful models used in NLP (and other areas). The vanishing gradient problem was originally discovered by Sepp Hochreiter in 1991 and has been receiving attention again recently due to the increased application of deep architectures.
To fully understand this part of the tutorial I recommend being familiar with how partial differentiation and basic backpropagation works. If you are not, you can find excellent tutorials here and here and here, in order of increasing difficulty.
Backpropagation Through Time (BPTT)
Let’s quickly recap the basic equations of our RNN. Note that there’s a slight change in notation from $o$ to $\hat{y}$. That’s only to stay consistent with some of the literature out there that I am referencing.
\[\begin{aligned} s_t &= \tanh(Ux_t + Ws_{t-1}) \\ \hat{y}_t &= \mathrm{softmax}(Vs_t) \end{aligned} \]
We also defined our loss, or error, to be the cross entropy loss, given by:
\[\begin{aligned} E_t(y_t, \hat{y}_t) &= - y_{t} \log \hat{y}_{t} \\ E(y, \hat{y}) &=\sum\limits_{t} E_t(y_t,\hat{y}_t) \\ & = -\sum\limits_{t} y_{t} \log \hat{y}_{t} \end{aligned} \]
Here, $y_t$ is the correct word at time step $t$, and $\hat{y_t}$ is our prediction. We typically treat the full sequence (sentence) as one training example, so the total error is just the sum of the errors at each time step (word).
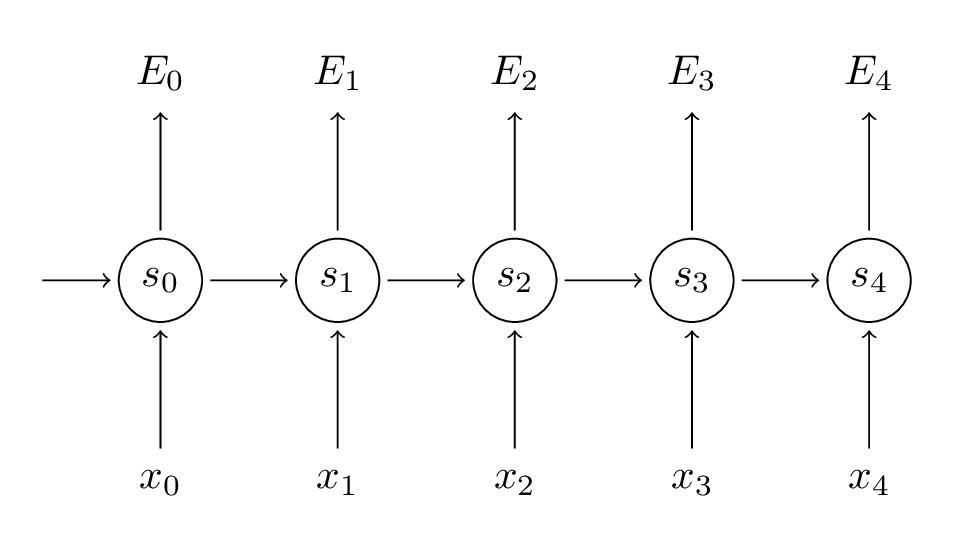
Remember that our goal is to calculate the gradients of the error with respect to our parameters $U,V$ and $W$ and then learn good parameters using Stochastic Gradient Descent. Just like we sum up the errors, we also sum up the gradients at each time step for one training example: $\frac{\partial E}{\partial W} = \sum\limits_{t} \frac{\partial E_t}{\partial W}$.
To calculate these gradients we use the chain rule of differentiation. That’s the backpropagation algorithm when applied backwards starting from the error. For the rest of this post we’ll use $E_3$ as an example, just to have concrete numbers to work with.
\[\begin{aligned} \frac{\partial E_3}{\partial V} &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial V}\\ &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial z_3}\frac{\partial z_3}{\partial V}\\ &=(\hat{y}_3 - y_3) \otimes s_3 \\ \end{aligned} \]
In the above, $z_3=Vs_3$, and $\otimes $ is the outer product of two vectors. Don’t worry if you don’t follow the above, I skipped several steps and you can try calculating these derivatives yourself (good exercise!). The point I’m trying to get across is that $\frac{\partial E_3}{\partial V} $ only depends on the values at the current time step, $\hat{y}_3, y_3, s_3 $. If you have these, calculating the gradient for $V$ a simple matrix multiplication.
But the story is different for $\frac{\partial E_3}{\partial W}$ (and for $U$). To see why, we write out the chain rule, just as above:
\[\begin{aligned} \frac{\partial E_3}{\partial W} &= \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial W}\\ \end{aligned} \]
Now, note that $s_3 = \tanh(Ux_t + Ws_2)$ depends on $s_2$, which depends on $W$ and $s_1$, and so on. So if we take the derivative with respect to $W$ we can’t simply treat $s_2$ as a constant! We need to apply the chain rule again and what we really have is this:
\[\begin{aligned} \frac{\partial E_3}{\partial W} &= \sum\limits_{k=0}^{3} \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \end{aligned} \]
We sum up the contributions of each time step to the gradient. In other words, because $W$ is used in every step up to the output we care about, we need to backpropagate gradients from $t=3$ through the network all the way to $t=0$:
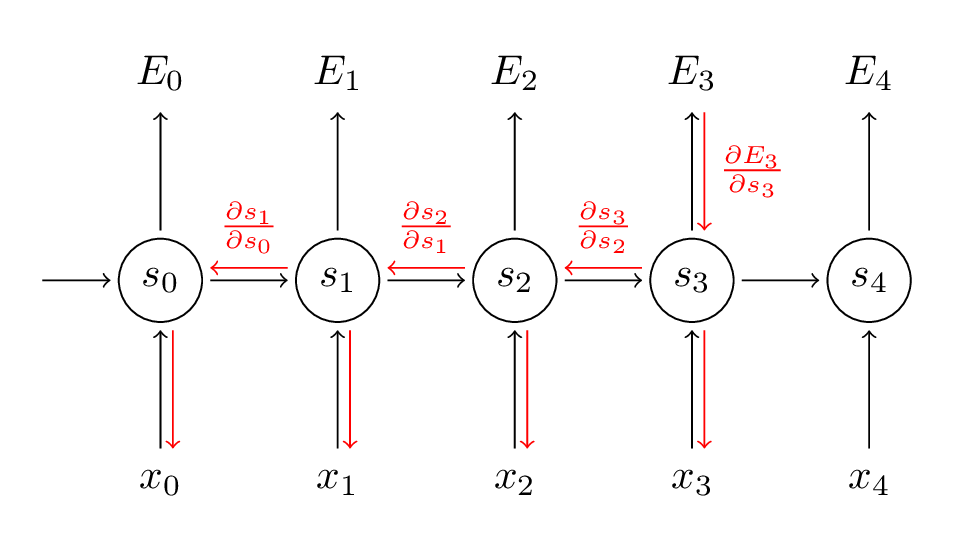
Note that this is exactly the same as the standard backpropagation algorithm that we use in deep Feedforward Neural Networks. The key difference is that we sum up the gradients for $W$at each time step. In a traditional NN we don’t share parameters across layers, so we don’t need to sum anything. But in my opinion BPTT is just a fancy name for standard backpropagation on an unrolled RNN. Just like with Backpropagation you could define a delta vector that you pass backwards, e.g.: $\delta_2^{(3)} = \frac{\partial E_3}{\partial z_2} =\frac{\partial E_3}{\partial s_3}\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial z_2}$ with $z_2 = Ux_2+ Ws_1$. Then the same equations will apply.
In code, a naive implementation of BPTT looks something like this:
def bptt(self, x, y):
T = len(y)
# Perform forward propagation
o, s = self.forward_propagation(x)
# We accumulate the gradients in these variables
dLdU = np.zeros(self.U.shape)
dLdV = np.zeros(self.V.shape)
dLdW = np.zeros(self.W.shape)
delta_o = o
delta_o[np.arange(len(y)), y] -= 1.
# For each output backwards...
for t in np.arange(T)[::-1]:
dLdV += np.outer(delta_o[t], s[t].T)
# Initial delta calculation: dL/dz
delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
# Backpropagation through time (for at most self.bptt_truncate steps)
for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
# print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
# Add to gradients at each previous step
dLdW += np.outer(delta_t, s[bptt_step-1])
dLdU[:,x[bptt_step]] += delta_t
# Update delta for next step dL/dz at t-1
delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
return [dLdU, dLdV, dLdW]
This should also give you an idea of why standard RNNs are hard to train: Sequences (sentences) can be quite long, perhaps 20 words or more, and thus you need to back-propagate through many layers. In practice many people truncate the backpropagation to a few steps.
The Vanishing Gradient Problem
In previous parts of the tutorial I mentioned that RNNs have difficulties learning long-range dependencies – interactions between words that are several steps apart. That’s problematic because the meaning of an English sentence is often determined by words that aren’t very close: “The man who wore a wig on his head went inside”. The sentence is really about a man going inside, not about the wig. But it’s unlikely that a plain RNN would be able capture such information. To understand why, let’s take a closer look at the gradient we calculated above:
\[\begin{aligned} \frac{\partial E_3}{\partial W} &= \sum\limits_{k=0}^{3} \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \end{aligned} \]
Note that $\frac{\partial s_3}{\partial s_k} $ is a chain rule in itself! For example, $\frac{\partial s_3}{\partial s_1} =\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial s_1}$. Also note that because we are taking the derivative of a vector function with respect to a vector, the result is a matrix (called theJacobian matrix) whose elements are all the pointwise derivatives. We can rewrite the above gradient:
\[\begin{aligned} \frac{\partial E_3}{\partial W} &= \sum\limits_{k=0}^{3} \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3} \left(\prod\limits_{j=k+1}^{3} \frac{\partial s_j}{\partial s_{j-1}}\right) \frac{\partial s_k}{\partial W}\\ \end{aligned} \]
It turns out (I won’t prove it here but this paper goes into detail) that the 2-norm, which you can think of it as an absolute value, of the above Jacobian matrix has an upper bound of 1. This makes intuitive sense because our $\tanh$ (or sigmoid) activation function maps all values into a range between -1 and 1, and the derivative is bounded by 1 (1/4 in the case of sigmoid) as well:
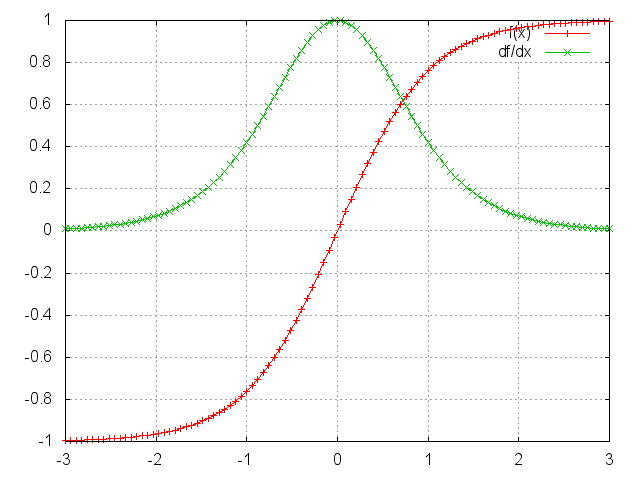
tanh and derivative.
You can see that the $\tanh$ and sigmoid functions have derivatives of 0 at both ends. They approach a flat line. When this happens we say the corresponding neurons are saturated. They have a zero gradient and drive other gradients in previous layers towards 0. Thus, with small values in the matrix and multiple matrix multiplications ($t-k$ in particular) the gradient values are shrinking exponentially fast, eventually vanishing completely after a few time steps. Gradient contributions from “far away” steps become zero, and the state at those steps doesn’t contribute to what you are learning: You end up not learning long-range dependencies. Vanishing gradients aren’t exclusive to RNNs. They also happen in deep Feedforward Neural Networks. It’s just that RNNs tend to be very deep (as deep as the sentence length in our case), which makes the problem a lot more common.
It is easy to imagine that, depending on our activation functions and network parameters, we could get exploding instead of vanishing gradients if the values of the Jacobian matrix are large. Indeed, that’s called the exploding gradient problem. The reason that vanishing gradients have received more attention than exploding gradients is two-fold. For one, exploding gradients are obvious. Your gradients will become NaN (not a number) and your program will crash. Secondly, clipping the gradients at a pre-defined threshold (as discussed in this paper) is a very simple and effective solution to exploding gradients. Vanishing gradients are more problematic because it’s not obvious when they occur or how to deal with them.
Fortunately, there are a few ways to combat the vanishing gradient problem. Proper initialization of the $W$ matrix can reduce the effect of vanishing gradients. So can regularization. A more preferred solution is to use ReLU instead of $\tanh$ or sigmoid activation functions. The ReLU derivative isn’t bounded by 1, so it isn’t as likely to suffer from vanishing gradients. An even more popular solution is to use Long Short-Term Memory (LSTM) or Gated Recurrent Unit (GRU) architectures. LSTMs were first proposed in 1997 and are the perhaps most widely used models in NLP today. GRUs, first proposed in 2014, are simplified versions of LSTMs. Both of these RNN architectures were explicitly designed to deal with vanishing gradients and efficiently learn long-range dependencies. We’ll cover them in the next part of this tutorial.
转载于:https://www.cnblogs.com/ZJUT-jiangnan/p/5234471.html
RNN 入门教程 Part 3 – 介绍 BPTT 算法和梯度消失问题相关推荐
- kettle详细使用oracle教程,Kettle入门教程(详细介绍控件使用方法)_kettle详细使用教程,kettle控件介绍...
Kettle入门教程(详细介绍控件使用方法)本手册主要是对Kettle工具的功能进行详细说明以及如何操作该系统,适合所有使用该系统的人员. 服务查询 数据库查询 数据库连接 流查询 调用存储过程 转换 ...
- ShaderToy入门教程(1) - SDF 和 Raymarching 算法
许多演示场景中使用的技术之一称为 光线追踪(Ray Marching) .该算法与一种称为 有符号距离函数 的特殊函数结合使用,可以实时创建一些非常酷的东西.这是系列教程,陆续推出,这篇涵盖以下黑体所 ...
- 【算法】梯度消失与梯度爆炸
概念 梯度不稳定 在层数比较多的神经网络模型的训练过程中会出现梯度不稳定的问题. 损失函数计算的误差通过梯度反向传播的方式,指导深度网络权值的更新优化.因为神经网络的反向传播算法是从输出层到输入层的逐 ...
- 算法基础--梯度消失的原因
深度学习训练中梯度消失的原因有哪些?有哪些解决方法? 1.为什么要使用梯度反向传播? 归根结底,深度学习训练中梯度消失的根源在于梯度更新规则的使用.目前更新深度神经网络参数都是基于反向传播的思想,即基 ...
- WPF真入门教程23--MVVM简单介绍
在WPF开发中,经典的编程模式是MVVM,是为WPF量身定做的模式,该模式充分利用了WPF的数据绑定机制,最大限度地降低了Xmal文件和CS文件的耦合度,也就是UI显示和逻辑代码的耦合度,如需要更换界 ...
- 浩辰3D设计软件新手入门教程:用户界面介绍
对于3D设计工程师来说, 3D设计软件作为日常不可或缺的工具,但是正在日常的设计工作中,为了更好更快的3D建模,最好选择一款好用的软件,浩辰3D软件具备和主流3D设计软件一致的用户界面,让工程师可以直 ...
- 简单实用的 TensorFlow 实现 RNN 入门教程
最近在看RNN模型,为简单起见,本篇就以简单的二进制序列作为训练数据,而不实现具体的论文仿真,主要目的是理解RNN的原理和如何在TensorFlow中构造一个简单基础的模型架构.其中代码参考了这篇博客 ...
- Python+Opencv图像处理新手入门教程(一):介绍,安装与起步
一步一步来吧 1.什么是opencv opencv: 是一个开源的计算机视觉库,它提供了很多函数,这些函数非常高效地实现了计算机视觉算法(最基本的滤波到高级的物体检测皆有涵盖). 使用 C/C++ 开 ...
- 易语言入门教程,工作界面介绍
下图是易语言打开后的界面点击新建才能看到窗口和控制台模块命令行的功能选择 下面是界面的介绍: 易语言窗口包含以下内容: 标题栏 菜单栏 工具栏(标准工具栏.对齐工具栏) 工作夹 状态夹 我们在以后的使 ...
最新文章
- 每一次宕机都是新的开始
- OVS datapath之action分析(十九)
- 关于box-shadow属性的一点心得
- 部署虚拟环境安装Linux系统(Linux就该这么学)笔记
- 数据预处理之将类别数据数字化的方法 —— LabelEncoder VS OneHotEncoder
- 给网页添加跟随你鼠标移动的线条动画
- java实时推送_JAVA 基于websocket的前台及后台实时推送
- 操作系统——概念、功能、特征及发展分类
- 清华大学计算机专业在职博士吧,清华大学在职博士含金量高吗?
- 如何下载天地图离线地图瓦片数据
- 计算机考研选择211还是重邮,22考研:这些容易但性价比高的院校专业千万别错过!...
- HTML+CSS伸缩式导航栏
- 配置 Eureka Server 集群
- Linux shell编程100例
- 乘法运算中的有效数据位
- Redis 的info命令信息解释
- 计算机视觉——SIFT描述子
- solidity第一课—了解Remix和Hellosolidity三行代码
- 【锐捷交换】交换机聚合接口配置
- bp前向传播和反向传播举例
