坐标离散化,imos
只是为了收藏一个很好的思路,算法。。。。
#include<alogrithm>
#include<vector>
#include<queue>
#include<iostream>
#include<cstring>
#define MAX_N 1000+16
using namespace std;
int N,H,W;
int x1[MAX_N],x2[MAX_N];,y1[MAX_N],y2[MAX_N];
int fid[2*MAX_N][2*MAX_N];
int dx[4]={1,-1,0,0},dy[4]={0,0,-1,1};
int compress(int *x1,int *x2,int w)
{vector<int>xs;for(i=0;i<N;i++){int tx1=x1[i],tx2=x2[i];if(1<=tx1&&tx1<W)xs.push_back(tx1);if(1<=tx2&&tx2<W)xs.push_back(tx2);}xs.push_back(0);xs.push_back(W);sort(xs.begin(),xs.end());xs.erase(unique(xs.begin(),xs.end()),xs.end());for(i=0;i<N;i++){x1[i]=find(xs.begin(),xs.end(),x1[i])-xs.begin();x2[i]=find(xs.begin(),xs.end(),x2[i])=xs.begin();}return xs.size()-1;
}
int bfs()
{int ans=0;for(int i=0;i<H;i++){for(int j=0;j<W;j++){if(fid[i][j])continue;ans++;queue<pair<int,int>>que;que.push(make_pair(j,i));while(!que.empty()){int nx=que.front().first,ny=que.front().second;que,pop();for(int i=0;i<4;i++){int tx=nx+d[i],ty=ny+dy[i];if(tx<0||W<tx||ty<0||H<ty||fid[ty][tx]>0)continue;que.push(make_pair(tx,ty));fid[tx][ty]=1;}}}}return ans;
}
int main()
{while(scanf("%d%d",&W,&H)&&W&&H){scanf("%d",&N);for(i=0;i<N;i++){scanf("%d%d%d%d",&x1[i],x2[i],y1[i],y2[i]);}memset(fid,0,sizeof(fid));W=compress(x1,x2,W);H=compress(y1,y2,H);for(i=0;i<N;i++){fid[y1[i]][x1[i]]++;fid[y1[i]][x2[i]]--;fid[y2[i]][x1[i]]++;fid[y2[i]][x2[i]]--;}for(int i=0;i<H;i++)for(int j=1;j<W;j++)fid[i][j]+=fid[i][j-1];for(int i=1;i<H;i++)for(j=0;j<W;j++)fid[i][j]+=fid[i-1][j];printf("%d\n",bfs());}
}以下是别人的帖子
for (int i = 0; i < T; i++) table[i] = 0;
for (int i = 0; i < C; i++) {// 時刻 S[i] から E[i] - 1 までのそれぞれについてカウントを 1 増やすfor (int j = S[i]; j < E[i]; j++) {table[j]++;}}// 最大値を調べるM = 0;for (int i = 0; i < T; i++) {if (M < table[i]) M = table[i];}
いもす法による解法
いもす法では,出入り口でのカウントのみをするという発想で入店時に +1 を,出店時に -1 を記録しておき,答えを求める直前に全体をシミュレートします.記録には O(C) が,シミュレートには O(T) がかかるので,全体としての計算量は O(C+T) となります.
for (int i = 0; i < T; i++) table[i] = 0;for (int i = 0; i < C; i++) {table[S[i]]++; // 入店処理: カウントを 1 増やすtable[E[i]]--; // 出店処理: カウントを 1 減らす}// シミュレートfor (int i = 0; i < T; i++) {if (0 < i) table[i] += table[i - 1];}// 最大値を調べるM = 0;for (int i = 0; i < T; i++) {if (M < table[i]) M = table[i];}
次元の拡張
いもす法の 1 番の特徴はナイーブな方法と比較して,次元の上昇に強いという点です.次元の呪いからは逃れられないので高次元に適用することは難しいですが,問題設定として 2 次元や 3 次元が用いられることは非常に多く,それらの状況においていもす法は有用です.
問題例
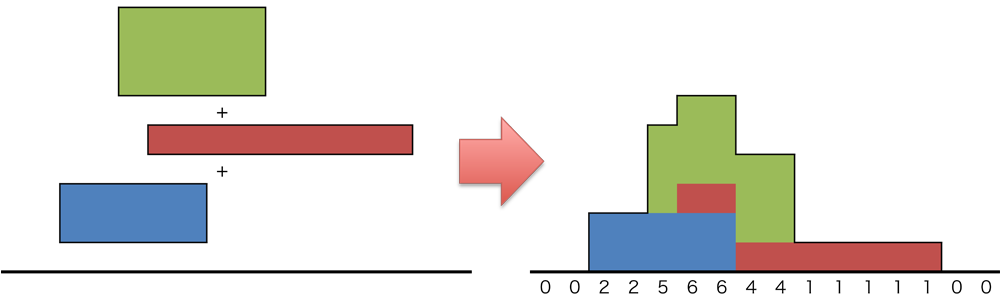
あなたは様々な種類のモンスターを捕まえるゲームをしています.今あなたがいるのは W×H のタイルからなる草むらです.この草むらでは N 種類のモンスターが現れます.モンスター i は Ai≦x<Bi, Ci≦y<Di の範囲にしか現れません.このゲームを効率的に進めるため,1 つのタイル上で現れるモンスターの種類の最大値が知りたいです.(ただし, W×H は計算可能な程度の大きさとし, N は大きくなりうるものとします.)
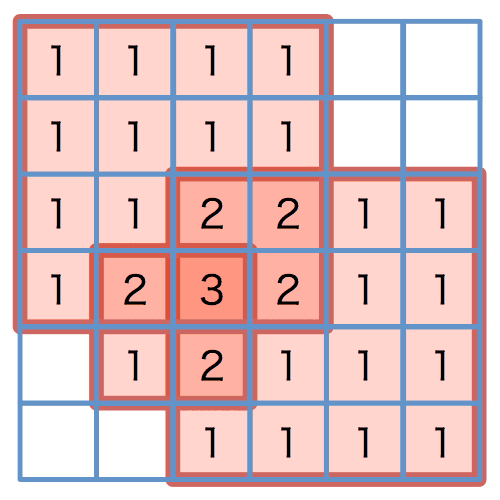
図 2: モンスターが現れる矩形(赤色)と,
各タイルで現れるモンスターの種類の数
ナイーブな解法
ナイーブな解法としては,それぞれのモンスターについて現れる矩形の範囲に含まれるすべてのタイルについて 1 を足す方法が挙げられます.しかし,これの計算量は O(NWH) です.
for (int y = 0; y < H; y++) {for (int x = 0; x < W; x++) {tiles[y][x] = 0;}}for (int i = 0; i < N; i++) {// モンスター i が現れる [(A[i],C[i]), (B[i],D[i])) の範囲に 1 を足すfor (int y = C[i]; y < D[i]; y++) {for (int x = A[i]; x < B[i]; x++) {tiles[y][x]++;}}}// 最大値を調べるint tile_max = 0;for (int y = 0; y < H; y++) {for (int x = 0; x < W; x++) {if (tile_max < tiles[y][x]) {tile_max = tiles[y][x];}}}
いもす法による解法
いもす法では,矩形の左上 (A[i],C[i]) に +1 を,右上 (A[i],D[i]) に −1 を,左下 (B[i],C[i]) に −1 を,右下 (B[i],D[i]) に +1 を加算し,答えを求める直前に累積和を求めます.記録には O(N) が,累積和の計算には O(WH) がかかるので,全体としての計算量は O(N+WH) となります.
for (int y = 0; y < H; y++) {for (int x = 0; x < W; x++) {tiles[y][x] = 0;}}// 重みの加算 (図 3)for (int i = 0; i < N; i++) {tiles[C[i]][A[i]]++;tiles[C[i]][B[i]]--;tiles[D[i]][A[i]]--;tiles[D[i]][B[i]]++;}// 横方向への累積和 (図 4, 5)for (int y = 0; y < H; y++) {for (int x = 1; x < W; x++) {tiles[y][x] += tiles[y][x - 1];}}// 縦方向の累積和 (図 6, 7)for (int y = 1; y < H; y++) {for (int x = 0; x < W; x++) {tiles[y][x] += tiles[y - 1][x];}}// 最大値を調べるint tile_max = 0;for (int y = 0; y < H; y++) {for (int x = 0; x < W; x++) {if (tile_max < tiles[y][x]) {tile_max = tiles[y][x];}}}
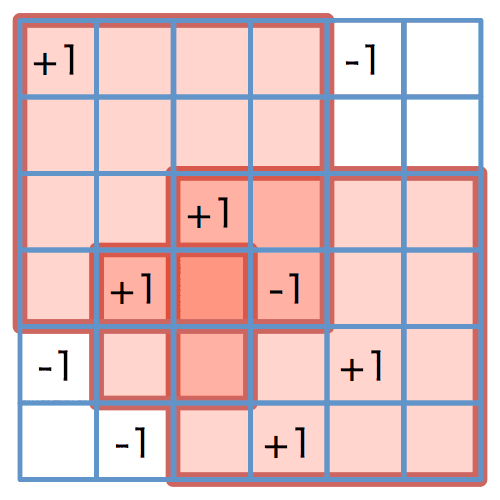
図 3: 重みの加算の結果
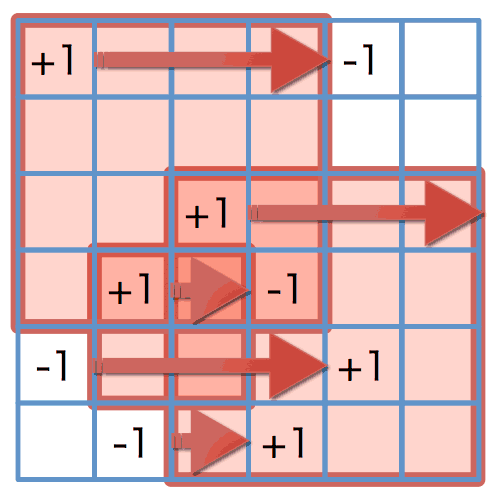
図 4: 横方向への累積
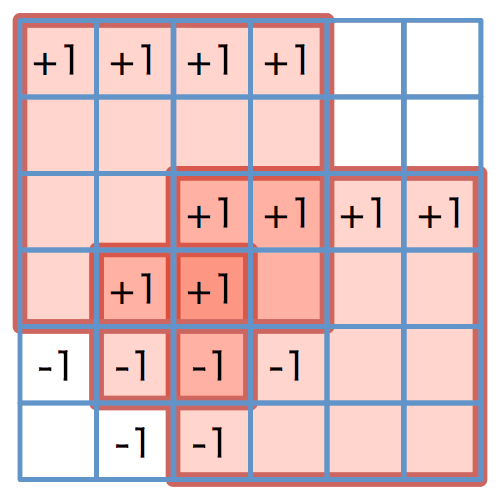
図 5: 横方向への累積の結果
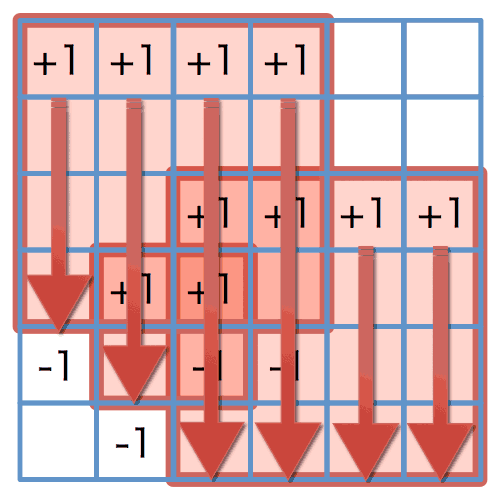
図 6: 縦方向への累積

図 7: 縦方向への累積の結果
特殊な座標系への拡張
いもす法は三角形や六角形の座標系にも適用できます.どこに重みを加算して,どのような方向に累積するのかは,目標となる形に対してできる限り数が少なくなるような方向に様々な方向に差分を取って見つけます.
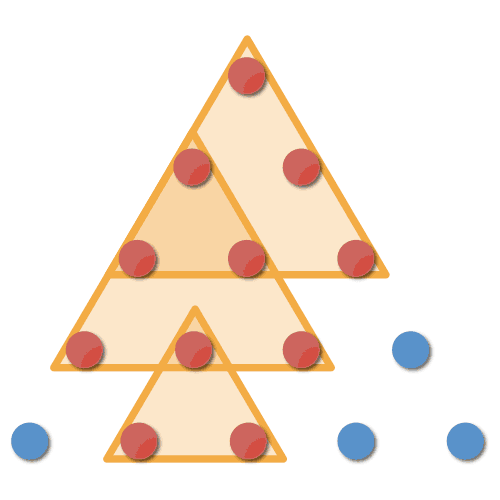
図 8: 三角形の座標系
差分を取る手法
図 9 は三角形の座標系において埋めるべき重みを表しています.緑の線は間が省略されていることを示します(一辺の長さが 4 である三角形の場合には線を無視してもこれらの図では同様の結果になります).いもす法でこのような重み付けを行うため,重みのあるセルの数が十分に少なくなるまで差分をとって,重みを付けるべきセルの配置と累積和をとる方向を知る必要があります. 図 9 〜 12 は差分をとる過程を表しています.これらの間に,「左上から右下への差分」「右上から左下への差分」「左から右への差分」をとったので,いもす法で三角形の累積和を求める場合は,図 12 のように数値を配置し逆の動作「左から右への累積和」「右上から左下への累積和」「左上から右下への累積和」を行います.
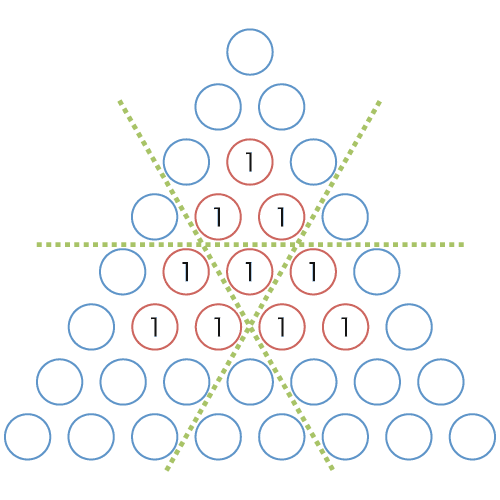
図 9: 埋めるべき重み
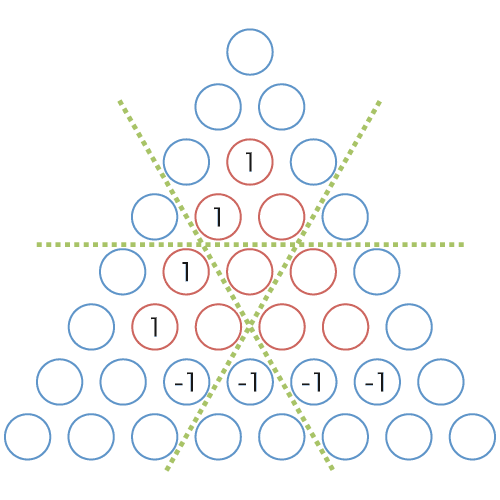
図 10: 図 9 の左上から右下への差分
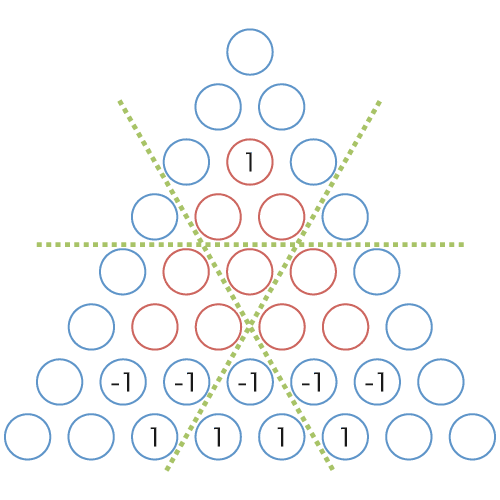
図 11: 図 10 の右上から左下への差分
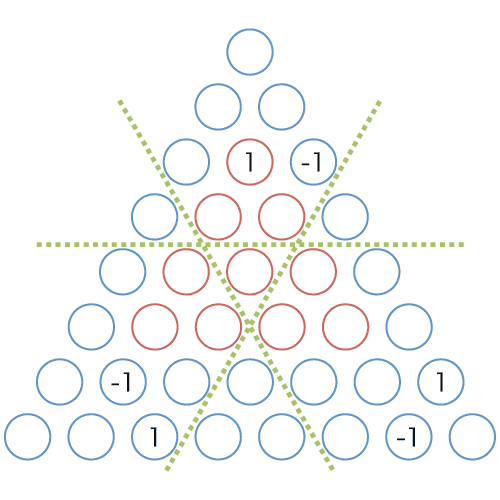
図 12: 図 11 の左から右への差分
同様の方法は三角形だけではなく,六角形の場合や,つける重みが定数ではなく傾き(ただし,多項式に限る)を持っている場合にも適用できます.
次数の拡張
競技プログラミングで出題される問題は高くとも 1 次までだとは思いますが,いもす法は高次の区分多項式関数も適用することができます.本来多項式で良い近似が得られないと思われている関数が区分多項式で表せられることがあり,それを利用すると連続ウェーブレット変換の高速化が可能になります.
2 次関数の差分
試しに 1 次元上で 2 次関数のいもす法を行なってみましょう.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 |
↓差分 ↑累積和
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
↓差分 ↑累積和
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
↓差分 ↑累積和
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
図 13: 2 次関数 (x−2)+2 の差分
図 13 より,2 次関数 (x−a)+2 を加算するとき,テーブルの a+1 および a+2 に 1 を加算し,最後に 3 度累積和をとることにより 2 次関数を用いた,いもす法が適用できることがわかります(ただし, (・)+=max(0,・) とする).同様の方法で,より高次の関数であっても,いもす法が適用可能です.
ガウス関数といもす法
次数の拡張の例としてガウス関数を見てみましょう.いもす法を適用するため,式 1 の左辺に表されるようなガウス関数を,右辺のような区分多項式で近似します.この近似関数は図 14 に示されるように非常によく近似されています.
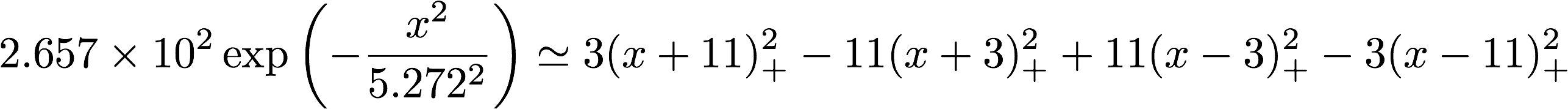
式 1: ガウス関数(左辺)とその近似(右辺)
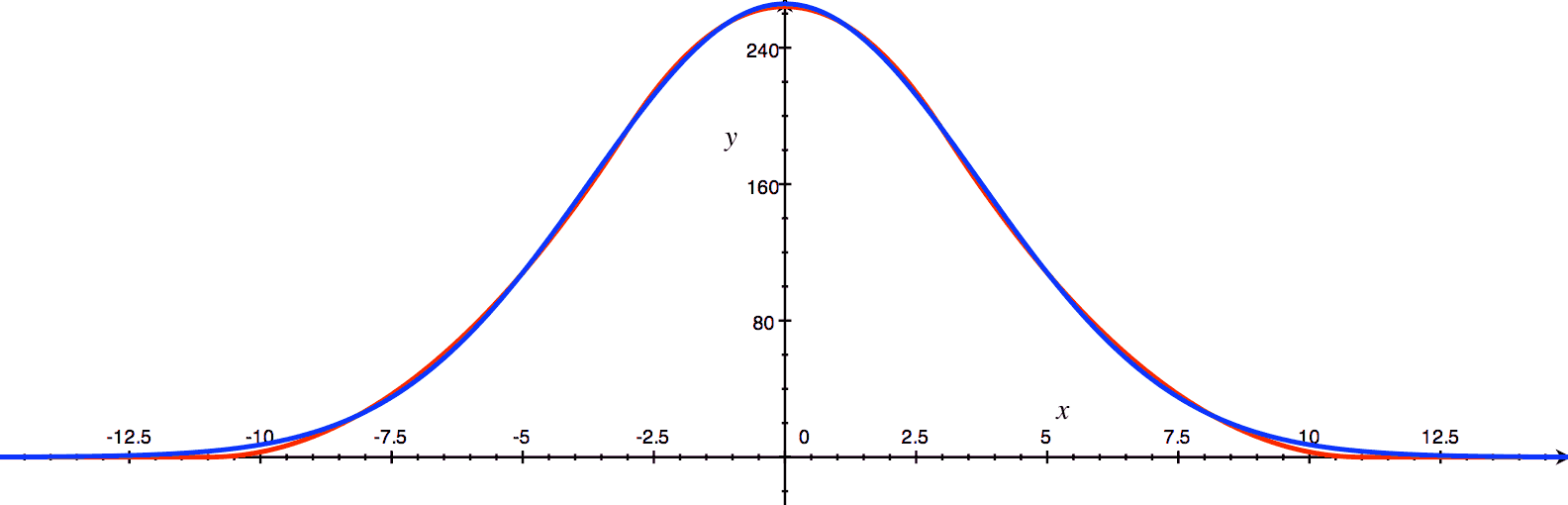
図 14: ガウス関数(青)と多項式近似(赤)
| -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | -11 | -11 | 0 | 0 | 0 |
↓累積和 ↑差分
| -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| 0 | 0 | 3 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | -5 | -16 | -16 | -16 | -16 |
↓累積和 ↑差分
| -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| 0 | 0 | 3 | 9 | 15 | 21 | 27 | 33 | 39 | 45 | 40 | 24 | 8 | -8 | -24 |
↓累積和 ↑差分
| -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| 0 | 0 | 3 | 12 | 27 | 48 | 75 | 108 | 147 | 192 | 232 | 256 | 264 | 256 | 232 |
図 15: いもす法によって近似されたガウス関数
| -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|
1 .49 |
3 .42 |
7 .28 |
14 .41 |
26 .57 |
45 .58 |
72 .76 |
108 .08 |
149 .41 |
192 .20 |
230 .09 |
256 .31 |
265 .70 |
256 .31 |
230 .09 |
図 16: 近似目標となるガウス関数
さらに, d 次元のガウス関数は 1 次元のガウス関数の積で表すことができるので, d 次元のいもす法が適用できます.またガウス関数は,中心からのユークリッド距離で重みが決まる(2 次元上では円形,3 次元上では球形である)ため,回転不変な値をとりたい時などに非常に有用です. これについてより詳しく知りたい場合は, ICPR 2012 での発表資料をご参照ください.
坐标离散化,imos相关推荐
- 算法复习之坐标离散化
离散化概念 例子: 1. 描述: 在桌子上放了N个平行于坐标轴的矩形,这N个矩形可能有互相覆盖的部分,求它们组成的图形的面积. 输入格式:输入第一行为一个数N(1<=N<=100),表示矩 ...
- hdu5925 Coconuts(坐标离散化)
题目 r*c(0<r,c<=1e9)的网格图,有n(0<=n<=200)个障碍点不能被访问,其余点是连通的, 输出这张网格图上的连通块的数量,按增序输出每个连通块的大小 思路来 ...
- CodeforcesBeta Round #19 D. Points 离线线段树 单点更新 离散化
题目链接: http://codeforces.com/contest/19/problem/D 题意: 有三种操作"add x y"往平面上添加(x,y)这个点,"re ...
- POJ 1177 Picture [离散化+扫描线+线段树]
http://poj.org/problem?id=1177 给若干矩形,求被覆盖的区域的周长. 将 y 坐标离散化后,按 x 坐标进行扫描.用线段树维护两个东西,当前竖线的叠加长度 len 和 条数 ...
- HDU - 1255 覆盖的面积(线段树求矩形面积交 扫描线+离散化)
链接:线段树求矩形面积并 扫描线+离散化 1.给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积. 2.看完线段树求矩形面积并 的方法后,再看这题,求的是矩形面积交,类同. 求面积时,用被覆 ...
- BZOJ #2874. 训练士兵(差分+离散化+主席树)
BZOJ #2874. 训练士兵 description solution code description Ryz正在着手于训练一批精锐士兵 Ryz手下有n*m个士兵,排成一个n行m列的方阵.在一天 ...
- HDU 1542 Atlantis 线段树+离散化+扫描线
题意:给出一些矩形的最上角坐标和右下角坐标,求这些矩形的面积并. NotOnlySuccess 线段树专辑中扫描线模板题,弱智的我对着大大的代码看了一下午才搞懂. 具体见思路见注释=.= #inclu ...
- poj3179 Corral the Cows(二分, 前缀和, 离散化, 双指针)
题目描述 农夫约翰希望为他的奶牛们建立一个畜栏. 这些挑剔的畜生要求畜栏必须是正方形的,而且至少要包含C单位的三叶草,来当做它们的下午茶. 畜栏的边缘必须与X,Y轴平行. 约翰的土地里一共包含N单位的 ...
- matlab 相机焦距,世界坐标、相机坐标、图像坐标、像素坐标的原理、关系,并用matlab仿真...
照相机是日常生活中最常见的.它能把三维的空间图片等比例缩小投影在照片上,称为一个二维图像. 以下我们就讲一讲原理,并相应的进行matlab仿真. 在学之前,先要了解几个概念: 什么是世界坐标? 也就是 ...
最新文章
- Python中如何拷贝一个对象?(赋值、深拷贝、浅拷贝的区别)
- BMP图片的解析,关于压缩方式
- Win7如何快速打开命令提示符
- 基本的SQL-SELECT语句练习
- python爬虫 爬取有道翻译详解
- Virtualbox中Ubuntu与windows共享文件夹设置
- C++中实例化一个类的方式
- 四叶草efi_Clover Configurator for Mac(四叶草配置引导工具)
- 水箱液位计算机控制系统设计,水箱水位PLC自动控制系统的设计_吕宁.pdf
- 北科大学计算机考研难度,2019二本考上北科计算机专硕经验分享
- KYLO的Java基础知识总结(其二)
- 怎么查微信公众号服务器,微信公众号查询数据库,微信公众号数据库怎么查询?...
- Python PTA实验课 输出星期名缩写+字典的创建
- vue单页面应用初始加载登录页_6 种 Vue 权限路由实现方式总结(最全)
- windows远程ubuntu键盘无法输入
- 蓝牙变成“未知USB设备”的解决方法
- android 仿微信demo————登录功能实现(服务端)
- 无效的列类型: 1111
- 24v转5v串多大电阻arduino
- 1602液晶显示器代码
