前言

2018年我写过一篇博客，叫：《一文读懂目标检测：R-CNN、Fast R-CNN、Faster R-CNN、YOLO、SSD》，该文相当于梳理了2019年之前CV领域的典型视觉模型，比如

2014 R-CNN
2015 Fast R-CNN、Faster R-CNN
2016 YOLO、SSD
2017 Mask R-CNN、YOLOv2
2018 YOLOv3

随着2019 CenterNet的发布，特别是2020发布的DETR(End-to-End Object Detection with Transformers)之后，自此CV迎来了生成式下的多模态时代(本文介绍其中有下划线的部分，其他部分下一篇介绍)

	1月	3月	4月	5月	6月	8月	10月	11月
2020				DETR	DDPM		DDIM VisionTransformer
2021	CLIP DALL·E	SwinTransformer						MAE SwinTransformerV2
2022	BLIP		DALL·E 2			StableDiffusion BEiT-3 Midjourney V3
2023	BLIP2	Visual ChatGPT GPT4 Midjourney V5	SAM(Segment Anything Model)

但看这些模型接二连三的横空出世，都不用说最后爆火的GPT4，便可知不少CV同学被卷的不行

说到GPT4，便不得不提ChatGPT，实在是太火了，改变了很多行业，使得国内外绝大部分公司的产品、服务都值得用LLM全部升级一遍(比如微软的365 Copilot、阿里所有产品、金山WPS等等)

而GPT4相比GPT3.5或GPT3最本质的改进就是增加了多模态的能力，使得ChatGPT很快就能支持图片的输入形式，从而达到图生文和文生图的效果，而AI绘画随着去年stable diffusion和Midjourney的推出，使得文生图火爆异常，各种游戏的角色设计、网上店铺的商品/页面设计都用上了AI绘画这样的工具，更有不少朋友利用AI绘画取得了不少的创收，省时省力还能赚钱，真香

但面对这么香的技术，其背后的一系列原理到底是什么呢，本文特从头开始，不只是简单的讲一下扩散模型的原理，而是在反复研读相关论文之后，准备把20年起相关的CV多模态模型全部梳理一遍，从VE、VAE、DDPM到ViT/Swin transformer、CLIP/BLIP，再到stable diffusion/Midjourney、GPT4，当然，实际写的时候，会分成两篇甚至多篇文章，比如

第一篇，即本文《AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、ViT/Swin transformer》
第二篇，即下篇《AIGC下的CV多模态原理解析：从CLIP/BLIP到stable diffusion/Midjourney、GPT4》

就当2020年之后的CV视觉发展史了，且过程中会尽可能写透彻每一个模型的原理，举两个例子

网上介绍VAE的文章都太数学化(更怕那种表面正确其实关键的公式是错的误导人)，如果更边推导边分析背后的理论意义(怎么来的出发点是什么为什么要这么做这么做的意义是什么)，则会更好理解，这就跟变介绍原理边coding实现会更好理解、理解更深一个道理
如果完全展开DDPM推导的所有细节，假定需要100步的话，本文正在朝展开80步而努力，截止5月份之前，绝大部分的中文资料只展开了60步(正在因为只展开了60%，让很多初学者卡到中途)，所以你害怕的不是公式，你只是怕公式的展开不够细致，毕竟对每一个人而言，公式展开越细致越不怕
(如果本文有任何一个公式展开的不够细致、不够一目了然，请随时指出，一定及时二次展开)

第一部分编码器VE与变分自编码器VAE

1.1 AE：编码器(数据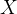 $X$ 压缩为低维表示 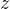$z$ )-解码器(低维表示恢复为原始数据 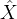$\hat{X}$ )架构

自编码器(Autoencoder，简称AE)是一种无监督学习的神经网络，用于学习输入数据的压缩表示。具体而言，可以将其分为两个部分：编码器和解码器

编码器：编码器是一个神经网络，负责将输入数据 $X$ （如图像、文本等）压缩为一个低维表示 $z$ ，且表示为 $z = g(X)$
解码器：解码器是另一个神经网络，负责将编码器生成的低维表示恢复为原始数据 $\hat{X}$ ，且表示为 $\hat{X} = f(z)$

从而最终完成这么一个过程： $X \rightarrow z \rightarrow \hat{X}$ ，而其训练目标即是最小化输入数据 $X$ 与解码器重建数据 $\hat{X}$ 之间的差异，所以自编码器常用的一个损失函数为 $l = || X - \hat{X} || ^2$

这个自编码的意义在于

模型训练结束后，我们就可以认为编码 $z$ 囊括了输入数据 $X$ 的大部分信息，也因此我们可以直接利用 $z$ 表达原始数据，从而达到数据降维的目的
解码器只需要输入某些低维向量 $z$ ，就能够输出高维的图片数据 $\hat{X}$ ，那我们能否把解码器模型直接当做生成模型，在低维空间中随机生成某些向量 $z$ ，再喂给解码器 $f(z)$ 来生成图片呢？

对于第二点，理论上可以这么做，但问题在于

绝大多数随机生成的 $z,f(z)$ 只会生成一些没有意义的噪声，之所以如此，原因在于没有显性的对 $z$ 的分布 $p(z)$ 进行建模，我们并不知道哪些 $z$ 能够生成有用的图片
而且我们用来训练 $f(z)$ 的数据是有限的， $f$ 可能只会对极有限的 $z$ 有响应。而整个低维空间又是一个比较大的空间，如果只在这个空间上随机采样的话，我们自然不能指望总能恰好采样到能够生成有用的图片的 $z$

有问题自然便得探索对应的解决方案，而VAE(自变分编码器，Variational Autoencoders)则是在AE的基础上，显性的对 $z$ 的分布 $p(z)$ 进行建模(比如符合某种常见的概率分布)，使得自编码器成为一个合格的生成模型

1.2 Variational AutoEncoder (VAE)

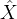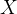1.2.1 VAE：标数据的分布 $\hat{X}$ 和目标分布 $X$ 尽量接近

VAE和GAN一样，都是从隐变量 $Z$ 生成目标数据，具体而言，先用某种分布随机生成一组隐变量 $Z = \left \{ Z_1,Z_2,\cdots ,Z_k \right \}$ (假设隐变量服从正态分布)，然后这个 $Z$ 隐变量经过一个生成器生成一组数据 $\hat{X} = \left \{ \hat{X_1},\hat{X_2},\cdots ,\hat{X_k} \right \}$ ，具体如下图所示(本1.2节的部分图来自苏建林)：

而VAE和GAN都希望这组生成数据的分布 $\hat{X}$ 和目标分布 $X$ 尽量接近，看似美好，但有两个问题

一方面，“尽量接近”并没有一个确定的关于 $\hat{X}$ 和 $X$ 的相似度的评判标准，比如KL散度便不行，原因在于KL散度是针对两个已知的概率分布求相似度的，而 $\hat{X}$ 和 $X$ 的概率分布目前都是未知(只有一批采样数据没有分布表达式)
二方面，经过采样出来的每一个 $Z_k$ ，不一定对应着每一个原来的 $X_k$ ，故最后没法直接最小化 $D^2(X_k,\hat{X_k})$

实际是怎么做的呢，事实上，与自动编码器由编码器与解码器两部分构成相似，VAE利用两个神经网络建立两个概率密度分布模型：

一个用于原始输入数据 $X=\{X_1,...,X_k\}$ 的变分推断，生成隐变量 $Z$ 的变分概率分布 $p(Z|X_k)$ ，称为推断网络
而VAE的核心就是，我们不仅假设 $p(Z)$ 是正态分布，而且假设每个 $p(Z|X_k)$ 也是正态分布。什么意思呢？即针对每个采样点 $X_k$ 获得一个专属于它和 $Z$ 的一个正态分布 $p(Z|X_k)$

换言之，有 $k$ 个 $X$ sample，就有 $k$ 个正态分布 $p(Z|X_k)$ ，毕竟没有任何两个采样点是完全一致的，而后面要训练一个生成器 $\hat{X_k}=f(Z)$ ，希望能够把从分布 $p(Z|X_k)$ 采样出来的一个 $Z_k$ 还原为 $X_k$ ，而如果从 $p(Z)$ 中采样一个 $Z_k$ ，没法知道这个 $Z_k$ 对应于真实的 $X_k$ 呢？现在 $p(Z|X_k)$ 专属于 $X_k$ ，我们有理由说从这个分布采样出来的 $Z_k$ 可以还原到对应的 $X_k$ 中去

而如何确定这 $k$ 个正态分布呢，众所周知，确定一个正太分布只需确定其均值 $u$ 和方差 $\sigma ^2$ 即可，故可通过已知的 $X_k$ 和假设的 $Z$ 去确定均值和方差
具体可以构建两个神经网络 $\mu _k = f_1(X_k)$ ， $log \sigma _{k}^{2} = f_2(X_k)$ 去计算。值得一提的是，选择拟合 $log \sigma _{k}^{2}$ 而不是直接拟合 $\sigma _{k}^{2}$ ，是因为 $\sigma _{k}^{2}$ 总是非负的，需要加激活函数处理，而拟合 $log \sigma _{k}^{2}$ 不需要加激活函数，因为它可正可负
另一个根据生成的隐变量 $Z$ 的变分概率分布 $p(Z)$ ，还原生成原始数据的近似概率分布 $p(\hat{X}|Z)$ ，称为生成网络
因为已经学到了这 $k$ 个正态分布，那可以直接从专属分布 $p(Z|X_k)$ 中采样一个 $Z_k$ 出来，然后经过一个生成器得到 $\hat{X_k} = f(Z_k)$ ，那接下来只需要最小化方差 $D^2(X_k,\hat{X_k})$ 就行

仔细理解的时候有没有发现一个问题？为什么在文章最开头，我们强调了没法直接比较 $X$ 与 $\hat{X}$ 的分布，而在这里，我们认为可以直接比较这俩？注意，这里的 $Z_k$ 是专属于或针对于 $X_k$ 的隐变量，那么和 $\hat{X_k}$ 本身就有对应关系，因此右边的蓝色方框内的“生成器”，是一一对应的生成。

另外，大家可以看到，均值和方差的计算本质上都是encoder。也就是说，VAE其实利用了两个encoder去分别学习均值和方差

1.2.2 VAE的Variational到底是个啥

这里还有一个非常重要的问题：由于我们通过最小化 $D^2(X_k,\hat{X_k})$ 来训练右边的生成器，最终模型会逐渐使得 $X_k$ 和 $\hat{X_k}$ 趋于一致。但是注意，因为 $Z_k$ 是重新随机采样过的，而不是直接通过均值和方差encoder学出来的，这个生成器的输入 $Z$ 是有噪声的

仔细思考一下，这个噪声的大小其实就用方差来度量。为了使得分布的学习尽量接近，我们希望噪声越小越好，所以我们会尽量使得方差趋于 0
但是方差不能为 0，因为我们还想要给模型一些训练难度。如果方差为 0，模型永远只需要学习高斯分布的均值，这样就丢失了随机性，VAE就变成AE了……这就是为什么VAE要在AE前面加一个Variational：我们希望方差能够持续存在，从而带来噪声！
那如何解决这个问题呢？其实保证有方差就行，但是VAE给出了一个优雅的答案：不仅需要保证有方差，还要让所有 $p(Z|X)$ 趋于标准正态分布 $N(0,1)$ ，根据定义可知
$P(Z) = \sum_{X}^{} p(Z|X)p(X) = \sum_{X}^{} N(0,1)p(X) = N(0,1)\sum_{X}p(X) = N(0,1)$

这个式子的关键意义在于告诉我吗：如果所有 $p(Z|X)$ 都趋于 $N(0,1)$ ，那么我们可以保证 $p(Z)$ 也趋于 $N(0,1)$ ，从而实现先验的假设，这样就形成了一个闭环！那怎么让所有 $p(Z|X)$ 趋于 $N(0,1)$ 呢？还是老套路：加loss

到此为止，我们可以把VAE进一步画成：

现在我们来回顾一下VAE到底做了啥。VAE在AE的基础上

一方面，对均值的encoder添加高斯噪声(正态分布的随机采样)，使得decoder(即生成器)有噪声鲁棒性
二方面，为了防止噪声消失，将所有 $p(Z|X)$ 趋近于标准正态分布，将encoder的均值尽量降为 0，而将方差尽量保持住

这样一来，当decoder训练的不好的时候，整个体系就可以降低噪声；当decoder逐渐拟合的时候，就会增加噪声

第二部分扩散模型DDPM：先前向加噪后反向去噪从而建立噪声估计模型

在写本文之前，我反复看了网上很多阐述DDPM的文章，实话说，一开始看到那种一上来就一堆公式的，起初基本看不下去，虽然后来慢慢的都看得下去了，但如果对于一个初次接触DDPM的初学者来说，一上来就一堆公式确实容易把人绕晕，但如果没有公式，则又没法透彻理解背后的算法步骤

两相权衡，本文将侧重算法每一步的剖析，而公式更多为解释算法原理而服务，说白了，侧重原理其次公式，毕竟原理透彻了，公式也就自然而然的能写出来了

言归正传，2020年，UC Berkeley等人的Jonathan Ho等人通过论文《Denoising Diffusion Probabilistic Models》正式提出DDPM(全称即论文名称：Denoising Diffusion Probabilistic Models，简称DDPM)

扩散模型的灵感来自非平衡热力学，通过定义了一个扩散步骤的马尔可夫链，以缓慢地将「符合高斯分布的随机噪声」添加到数据中，然后反转扩散过程以从噪声中构建所需的数据样本

每一个噪声都是在前一时刻增加噪声而来的，从最开始的 $x_0$ 时刻开始，最终得到 $x_T$ 时刻的纯噪声图像。不过问题来是为什么要加噪声？

Diffusion的最终目标是去噪以生成图片，而为了推导出逆向的去噪方法，必须了解增加噪声的原理。同时，添加噪声的过程其实就是不断构建标签的过程。如果在前一时刻可以预测出来后一时刻的噪声，便能很方便地实现还原操作(就和人走路一样，不管你从哪来，哪怕走过万水千山，最后都可按原路返回至原出发点)
说白了 当你学会了怎么加噪(前向扩散)，就一定能知道怎么去噪(逆向生成)，毕竟知道怎么来也必知道怎么回
且在噪声的添加过程中，每一步都要保持尽量相同的噪声扩散幅度。比如，在给上图加噪的过程中，前期的分布非常均匀，添加一些噪声便可以将原始分布改变，但到后期，需要添加更多的噪声，方可保证噪声扩散幅度相同(这就像往水中加糖，为了使糖的甜味增长相同，后期需要加更多的糖)

所以DDPM为了从随机噪声中直接生成图片，首先需要训练一个噪声估计模型，然后将输入的随机噪声还原成图片，相当于就两个关键，一个是训练过程，一个是推理过程

训练过程：随机生成噪声 $\epsilon$ ，经过 $T$ 步将噪声扩散到输入原始图片 $x_0$ 中，破坏后的图片 $x_T$ ，学习破坏图片的预估噪声 $\epsilon _\theta (x_t,t)$ ，用L2 loss约束与 $\epsilon$ 原始输入噪声的距离
推理过程：即输入噪声，经过预估噪声模型还原成图片

2.1 DDPM的两个过程：从前向过程到逆向过程

2.1.1 前向过程(加噪)：通过高斯噪音随机加噪 $\epsilon$ ——给图片打马赛克

前向过程(forward process)也称为扩散过程(diffusion process)，简单理解就是对原始图片 $x_0$ 通过逐步添加「方差为 $\beta _t$ 的高斯噪声」变成 $x_T$ ，从而达到破坏图片的目的，如下图

在从 $x_{t-1}$ 到 $x_t$ 的过程中，其对应的分布 $q(x_t|x_{t-1})$ 是一个正太分布，且其均值是 $u_t = \sqrt{1-\beta _t }x_{t-1}$ ，方差为 $\beta _t$ ，则有

$q(x_t|x_{t-1}) = N(x_t;u_t = \sqrt{1-\beta _t }x_{t-1},\beta _t \mathbb{I})$

对于这个公式，解释下3点

正态分布的概率密度函数具有以下形式：

$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

正态分布有两个参数：均值 $\mu$ 和方差 $\sigma ^2$ 。其中， $\mu$ 是分布的均值，决定了分布的中心位置， $\sigma$ 是标准差，决定了分布的宽度
上面的方差之所以表示为 $\beta _t \mathbb{I}$ ，原因在于我们一般处于多维情况下，而 $\mathbb{I}$ 是单位矩阵，表明每个维度有相同的标准偏差 $\beta _t$
且 $\beta _t \in (0,1)$ 是事先给定的常量，代表从 $x_{t-1}$ 到 $x_t$ 这一步的方差，且正因为 $\beta _t$ 设置的比较小，所以使得 $q(x_t|x_{t-1})$ 的均值在 $x_{t-1}$ 附近，换言之， $x_t$ 相当于就是在 $x_{t-1}$ 的基础上加了一些噪声，而且是渐进式逐步增加/扩散的，当然从加噪大小的角度上讲，前期加噪较弱，后期加噪加强，所以在DDPM的论文中，作者取 $\beta _1,\cdots \beta _T$ 为从0.0001到0.02的线性递增序列
此外，值得一提的是，因为是马尔可夫链，所以其联合分布便是：
$q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)=q\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{T} \mid \mathbf{x}_{0}\right)=\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$
如下图所示

接下来，如果我们定义 $\alpha _t = 1 - \beta_t$ , 且 $\left \{ {\alpha_t} \right \}_{t=1}^{T}$ 『被称为Noise schedule，通常是一些列很小的值』，以及 $\epsilon _{t-1} \sim N(0,1)$ 是高斯噪声，便可以得到 $x_t$ 的采样值

$x_t = \sqrt{\alpha _t}x_{t-1} + \sqrt{1-\alpha _t} \epsilon _{t-1}$

把上述公式迭代变换下，可以直接得出 $x_0$ 到 $x_t$ 的公式，如下：

$x_t = \sqrt{\bar{\alpha _t}}x_{0} + \sqrt{1-\bar{\alpha _t}} \epsilon$

其中 $\bar{\alpha _t} = \prod_{i=1}^{t} \alpha _i$ ， $\epsilon \sim N(0,1)$ 也是一个高斯噪声

换言之，所以 $x_t$ 在 $x_0$ 条件下的分布就是均值为 $\sqrt{\bar{\alpha _t}}x_0$ , 方差为 $1-\bar{\alpha _t}$ 的正态分布

$q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right)$

考虑到可能会有读者对这个 $x_0$ 到 $x_t$ 的一步到位感到困惑，而一般的同类文章不会展开的特别细，故本文细致展开下(能拆10步则10步确保阅读无障碍)

首先通过 $x_t = \sqrt{\alpha _t}x_{t-1} + \sqrt{1-\alpha _t} \epsilon _{t-1}$ 可知， $x_{t-1} = \sqrt{\alpha _{t-1}}x_{t-2} + \sqrt{1-\alpha _{t-1}} \epsilon _{t-2}$ ，把这个代入到 $x_t$ 的表达式后，再展开即可得
$\begin{aligned} \boldsymbol{x}_{t} & =\sqrt{\alpha_{t}} \boldsymbol{x}_{t-1}+\sqrt{1-\alpha_{t}} \boldsymbol{\epsilon}_{t-1}^{*} \\ & =\sqrt{\alpha_{t}}\left(\sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{1-\alpha_{t-1}} \boldsymbol{\epsilon}_{t-2}^{*}\right)+\sqrt{1-\alpha_{t}} \epsilon_{t-1}^{*} \\ & =\sqrt{\alpha_{t} \alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{\alpha_{t}-\alpha_{t} \alpha_{t-1}} \boldsymbol{\epsilon}_{t-2}^{*}+\sqrt{1-\alpha_{t}} \epsilon_{t-1}^{*} \end{aligned}$

考虑到「两个独立正态分布的随机变量之和是正态的，其均值是两个均值之和，其方差是两个方差之和（即标准差的平方是标准差的平方），比如两个方差不同的高斯分布 $\mathcal{N}(\mathbf{0}, \sigma_1^2\mathbf{I})$ 和 $\mathcal{N}(\mathbf{0}, \sigma_2^2\mathbf{I})$ 相加等于一个新的高斯分布 $\mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2)\mathbf{I})$ 」，然后再通过重参数技巧可得
$x_t \begin{array}{l} =\sqrt{\alpha_{t} \alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{{\sqrt{\alpha_{t}-\alpha_{t} \alpha_{t-1}}}^{2}+{\sqrt{1-\alpha_{t}}}^{2}} \boldsymbol{\epsilon}_{t-2} \\ =\sqrt{\alpha_{t} \alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{\alpha_{t}-\alpha_{t} \alpha_{t-1}+1-\alpha_{t}} \boldsymbol{\epsilon}_{t-2} \\ =\sqrt{\alpha_{t} \alpha_{t-1}} \boldsymbol{x}_{t-2}+\sqrt{1-\alpha_{t} \alpha_{t-1}} \boldsymbol{\epsilon}_{t-2} \\ =\ldots \end{array}$

对此，本文参考文献中的这篇《Understanding Diffusion Models: A Unified Perspective》也解释了这几个步骤

最后定义一个累积混合系数， $\bar{\alpha _t} = \prod_{i=1}^{t}\alpha _i$ ，即 $\sqrt{\bar{\alpha _t}} = \sqrt{\alpha _t} \sqrt{\alpha _{t-1}} \cdots \sqrt{\alpha _1}$ ，可得
$x_t \begin{array}{l} =\sqrt{\prod_{i=1}^{t} \alpha_{i}} \boldsymbol{x}_{0}+\sqrt{1-\prod_{i=1}^{t} \alpha_{i} \boldsymbol{\epsilon}_{0}} \\ =\sqrt{\bar{\alpha}_{t}} \boldsymbol{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_{0} \\ \sim \mathcal{N}\left(\boldsymbol{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \boldsymbol{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right) \end{array}$

2.1.2 逆向过程(去噪)：求解真实后验分布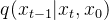 $q(x_{t-1}|x_t, x_0)$ —— 复原被加噪的图片使之清晰化

逆向过程就是通过估测噪声，多次迭代逐渐将被破坏的 $x_t$ 恢复成 $x_0$ ，如下图

更具体而言，正向扩散和逆扩散过程都是马尔可夫，唯一的区别就是正向扩散里每一个条件概率的高斯分布的均值和方差都是已经确定的（依赖于 $\beta _t$ 和 $x_0$ ），而逆扩散过程里面的均值和方差需要通过网络学出来，怎么个学法呢？

有人可能要说，直接把上一节得到的 $x_t = \sqrt{\bar{\alpha_t}}x_{0} + \sqrt{1-\bar{\alpha_t}} \epsilon$ 移个项不就行了(先把带 $x_0$ 的项移到等式左边，然后所有项各自除以 $\sqrt{\bar{\alpha }}$ ，最后把等式右边的 $1/\sqrt{\bar{\alpha }}$ 提取到括号外边即可)？
$\mathbf{x}_{0}=\frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon\right)$
但问题在于 $x_t = \sqrt{\bar{\alpha_t}}x_{0} + \sqrt{1-\bar{\alpha_t}} \epsilon$ 中的 $\epsilon$ 是个随机变量，意味着 $x_t$ 也是个随机变量，其具体取值由 $\epsilon$ 实际取值决定「相当于现在我们有一个具体的 $x_t$ ，它对应着 $\epsilon$ 的某个取值，但是什么值我们并不知道」，所以我们只能以前向过程的 $\epsilon$ 取值为标签，训练一个模型去估计它，即：
$\mathbf{x}_{\theta}\left(\mathbf{x}_{t}, t\right):=\frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right)$
其中 $\epsilon_\theta (x_t, t)$ 就是所谓的模型，用来近似真实的(即前向过程采样出来的) $\epsilon$ ；相应地， $\mathbf{x}_{\theta}\left(\mathbf{x}_{t}, t\right)$ 就是 $x_0$ 的近似。或者，你也可以无视 $\epsilon$ ，直接把 $\mathbf{x}_{\theta}\left(\mathbf{x}_{t}, t\right)$ 视为模型
为了训练它，最直接的想法就是用 L2 损失 $\left\|\epsilon-\epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}$ 或者 $\left\|\mathbf{x}_{0}-\mathbf{x}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}$

理论上没问题，但是实际效果很差，为什么呢？如果直接用 $\mathbf{x}_{\theta}\left(\mathbf{x}_{t}, t\right)$ ，那么中间的 $\mathbf{x}_{2}, \mathbf{x}_{3}, \ldots, \mathbf{x}_{T-1}$ 都没用了，整个 DDPM 就退化成了 VAE 的结构
但是 VAE 的生成模型和后验都是自己学习出来的，二者双向奔赴共同优化去寻找最优解；而 DDPM 的后验是人为指定的（即 $\mathbf{x}_{0} = 1/{\sqrt{\bar{\alpha}_{t}}}\left(\mathbf{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon\right)$ ），并且由于 $\bar{\alpha}_{t} \rightarrow 0$ ， $q(x_t|x_0)$ 基本上就是一个标准正态分布，磨灭掉了几乎所有的输入信息，全靠生成模型这一边去恢复，难度未免也..
所以，实际应用中，我们是一点一点来的，比如先生成 $x_{t-1}$ 、然后 $x_{t-2}$ ……由于每一步的变化都比较小，保留了上一步足够的信息，生成模型的负担就轻了很多
如果我们能够逆转前向过程并从真实分布 $q(x_{t-1}|x_t)$ 采样，就可以从高斯噪声 $x_t \sim N( 0, I )$ 还原出原图分布 $x_0 \sim q(x)$ 。因为我们可以证明如果前向 $q(x_t|x_{t-1})$ 满足高斯分布且 $\beta _t$ 足够小，其逆向 $q(x_{t-1}|x_t)$ 仍然是一个高斯分布

那样，我们便可以使用「参数为 θ 的U-Net+attention 结构 $p_\theta$ 」去预测这样的一个逆向的分布(类似VAE)：
$p_{\theta}\left(X_{0: T}\right)=p\left(x_{t}\right) \prod_{t=1}^{T} p_{\theta}\left(x_{t-1} \mid x_{t}\right)$
$p_{\theta}\left(x_{t-1} \mid x_{t}\right)=\mathcal{N}\left(x_{t-1} ; \mu_{\theta}\left(x_{t}, t\right), \Sigma_{\theta}\left(x_{t}, t\right)\right)$
不过在DDPM的论文中，作者把条件概率 $p_\theta (x_{t-1}|x_t)$ 的方差直接取了 $\beta _t$ ，而不是上面说的需要网络去估计的 $\Sigma_{\theta}\left(x_{t}, \mathrm{t}\right)$ ，所以说实际上只有均值需要网络去估计
然现在的问题是，我们无法直接去推断 $q(x_{t-1}|x_t)$

所以，接下来的问题自然而然就转换成了我们希望求解 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ ，因为我们知道前向过程 $q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$ ，所以自然想到使用贝叶斯公式：

$q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right) q\left(\mathbf{x}_{t-1}\right)}{q\left(\mathbf{x}_{t}\right)}$

可惜 $q(x_t)$ 和 $q(x_{t-1})$ 是未知的，事情到这里似乎走入了僵局，但是我们敏锐地发现 $q(x_t|x_0)$ 和 $q(x_{t-1}|x_0)$ 是已知的，如果给上式加上 $x_0$ 为条件，则立马柳暗花明，且如果知道 $x_0,q(x_{t-1}|x_t, x_0)$ 就可以直接写出 $q\left(x_{t-1} \mid x_{t}, x_{0}\right)=\mathcal{N}\left(x_{t-1} ; \tilde{\mu}\left(x_{t}, x_{0}\right), \tilde{\beta}_{t} \mathbf{I}\right)$

接下来，我们便好好推导下

解释下上面7.1~7.5这5个步骤的推导

7.1依据的是
$P(A|B) = \frac{P(AB)}{P(B)}$

7.2中，分母部分依据的是
$P(AB) = P(A)P(B|A)$
分子部分依据的是
$P(ABC)=P(A)P(B|A)P(C|AB)$

7.3依据的是分子分母同时除以 $q(x_0)$

至于7.3到7.4
$\begin{array}{l} =q\left(x_{t} \mid x_{t-1}, x_{0}\right) \frac{q\left(x_{t-1} \mid x_{0}\right)}{q\left(x_{t} \mid x_{0}\right)} \quad 7.3 \\ \propto \exp \left(-\frac{1}{2}\left(\frac{\left(x_{t}-\sqrt{\alpha_{t}} x_{t-1}\right)^{2}}{\beta_{t}}+\frac{\left(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}} x_{0}\right)^{2}}{1-\bar{a}_{t-1}}-\frac{\left(x_{t}-\sqrt{\bar{\alpha}_{t}} x_{0}\right)^{2}}{1-\bar{a}_{t}}\right)\right) \quad 7.4 \end{array}$
依据的是
$\rho(\mathrm{x})=\frac{1}{\sqrt{2 \pi \sigma}} \mathrm{e}^{-\frac{1}{2}\left(\frac{\mathrm{x}-\mu}{\sigma}\right)^{2}}$
且由前向扩散过程的特性『别忘了2.1.2节中，有 $q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right)$ 』，可知
$q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}, \mathbf{x}_{0}\right)=q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{1-\beta_{t}} \mathbf{x}_{t-1}, \beta_{t} \mathbf{I}\right)$
$q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t-1}\right) \mathbf{I}\right)$
$q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right)$

最后，再解释下怎么从7.4到的7.5
$\begin{array}{l} =q\left(x_{t} \mid x_{t-1}, x_{0}\right) \frac{q\left(x_{t-1} \mid x_{0}\right)}{q\left(x_{t} \mid x_{0}\right)} \quad 7.3 \\ \propto \exp \left(-\frac{1}{2}\left(\frac{\left(x_{t}-\sqrt{\alpha_{t}} x_{t-1}\right)^{2}}{\beta_{t}}+\frac{\left(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}} x_{0}\right)^{2}}{1-\bar{a}_{t-1}}-\frac{\left(x_{t}-\sqrt{\bar{\alpha}_{t}} x_{0}\right)^{2}}{1-\bar{a}_{t}}\right)\right)\\ =\exp \left(-\frac{1}{2}(\underbrace{\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) x_{t-1}^{2}}_{x_{t-1} \text {}}-\underbrace{\left(\frac{2 \sqrt{\alpha_{t}}}{\beta_{t}} x_{t}+\frac{2 \sqrt{\bar{a}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_{0}\right) x_{t-1}}_{\text {}x_{t-1}\text{}}+\underbrace{C\left(x_{t}, x_{0}\right)})\right) \cdot 7.5 \end{array}$
先举一个最简单的例子，比如对于 $\frac{1}{2} (Ax^2 + Bx + C)$ ，稍加转化下即是 $\frac{1}{2} A(x + \frac{B}{2A})^2 + C$ ，则其均值为 $- \frac{B}{2A}$ ，方差为 $\frac{1}{A}$
而这个 $A$ 则对应于7.5中的
$\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}$
$B$ 则对应于7.5中的
$- (\frac{2 \sqrt{\alpha_{t}}}{\beta_{t}} x_{t}+\frac{2 \sqrt{\bar{a}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_{0} )$
从而有
$\mu_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right)=\frac{-B}{2 A}$
$\begin{array}{l} =\left(\frac{\sqrt{\alpha_{t}}}{\beta_{t}} \mathbf{x}_{t}+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_{0}\right) /\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \\ =\left(\frac{\sqrt{\alpha_{t}}}{\beta_{t}} \mathbf{x}_{t}+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_{0}\right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t} \\ =\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_{t}} \mathbf{x}_{t}+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{1-\bar{\alpha}_{t}} \mathbf{x}_{0} \end{array}$
$\tilde{\beta _t} = \frac{1}{A} = 1 /\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_{t}-\bar{\alpha}_{t}+\beta_{t}}{\beta_{t}\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t}$

好，接下来关键来了

根据 $x_t = \sqrt{\bar{\alpha }_t} x_0 + \sqrt{1 - \bar{\alpha }_t} \epsilon$ ，可知 $x_{0}=\frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(x_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{t}\right)$ ，代入上面 $\mu _t(x_t,x_0)$ 的表达式可得

${\mu}(x_t,x_0)=\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}{\epsilon_t}\right)$

大部分对这个的推导都是一步到位的，但本文为细致起见，故还是一步步来推导下

首先直接把 $x_{0}=\frac{1}{\sqrt{\bar{\alpha}_{t}}}\left(x_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{t}\right)$ 和 $\beta _t = 1-\alpha _t$ 代入进去，可得

$\begin{aligned} \boldsymbol{\mu}_{}\left(\boldsymbol{x}_{t}, \boldsymbol{x}_{0}\right) & =\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_{t}+\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_{t}\right) \boldsymbol{x}_{0}}{1-\bar{\alpha}_{t}} \\ & =\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_{t}+\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_{t}\right) \frac{\boldsymbol{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{0}}{\sqrt{\bar{\alpha}_{t}}}}{1-\bar{\alpha}_{t}} \end{aligned}$
接下来，我们可以进一步观察到分子中的后半部分有 $\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_{t}\right) \frac{\boldsymbol{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{0}}{\sqrt{\bar{\alpha}_{t}}}$ 这一项，怎么进一步化简呢『接下来非常关键(截止23年5月份之前，暂时没看到有其他中英文资料解释了这个细节)』？
好在之前有定义： $\bar{\alpha _t} = \prod_{i=1}^{t}\alpha _i$ ，即 $\sqrt{\bar{\alpha _t}} = \sqrt{\alpha _t} \sqrt{\alpha _{t-1}} \cdots \sqrt{\alpha _1}$ ，从而有 $\sqrt{\bar{\alpha_t}} = \sqrt{\alpha_t} \sqrt{\bar{\alpha_{t-1}}}$

所以我们可以针对这一项 $\sqrt{\bar{\alpha}_{t-1}}\left(1-\alpha_{t}\right) \frac{\boldsymbol{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{0}}{\sqrt{\bar{\alpha}_{t}}}$ 的分子分母同时除以 $\sqrt{\bar{\alpha_{t-1}}}$ ，得到

$\mu _t(x_t,x_0) = \frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_{t}+\left(1-\alpha_{t}\right) \frac{\boldsymbol{x}_{t}-\sqrt{1-\bar{\alpha}_{t}} \epsilon_{0}}{\sqrt{\alpha_{t}}}}{1-\bar{\alpha}_{t}}$
之后的推导就比较简单了

$u(x_t,x_0) \begin{array}{l} =\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right) \boldsymbol{x}_{t}}{1-\bar{\alpha}_{t}}+\frac{\left(1-\alpha_{t}\right) \boldsymbol{x}_{t}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}}-\frac{\left(1-\alpha_{t}\right) \sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_{0}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}} \\ =\left(\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_{t}}+\frac{1-\alpha_{t}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}}\right) \boldsymbol{x}_{t}-\frac{\left(1-\alpha_{t}\right) \sqrt{1-\bar{\alpha}_{t}}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0} \\ =\left(\frac{\alpha_{t}\left(1-\bar{\alpha}_{t-1}\right)}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}}+\frac{1-\alpha_{t}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}}\right) \boldsymbol{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}} \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0} \end{array}$

以下分别对上面的三行公式做解释说明：
$\rightarrow$ 接着把上阶段2得到的式子的分子拆成三项，且三项中最后两项的分子分母同时乘以 $\sqrt{\alpha _t}$
$\rightarrow$ 然后再把上一步骤中分子三项中的前两项通过提取出 $x_t$ 从而实现合并
$\rightarrow$ 前两项合并之后，再对前两项中第一项的分子分母同时乘以 $\sqrt{\alpha _t}$ ，然后对第三项的分子分母同时除以 $\sqrt{1-\alpha _t}$ ，即可得 $\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}} \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0}$ ，原因很简单，因为： $1-\bar{\alpha_t} = \left ( \sqrt{1-\bar{\alpha _t}} \right )^2$
接下来，针对上面阶段3得到的式子的前两项再做合并，合并中用到了一个细节，即 $\alpha _t \times \bar{\alpha _{t-1}} = \bar{\alpha _t}$ ，原因也同样很简单，根据上面阶段2出现的这个式子 $\sqrt{\bar{\alpha_t}} = \sqrt{\alpha_t} \sqrt{\bar{\alpha_{t-1}}}$ 而来，再之后就更eazy 便不再赘述了

$\mu(x_t,x_0) \begin{array}{l} =\frac{\alpha_{t}-\bar{\alpha}_{t}+1-\alpha_{t}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}} \boldsymbol{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}} \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0} \\ =\frac{1-\bar{\alpha}_{t}}{\left(1-\bar{\alpha}_{t}\right) \sqrt{\alpha_{t}}} \boldsymbol{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}} \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0} \\ =\frac{1}{\sqrt{\alpha_{t}}} \boldsymbol{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}} \sqrt{\alpha_{t}}} \boldsymbol{\epsilon}_{0} \end{array}$

从最终得到的结果可以看出，在给定 $x_0$ 的条件下

后验条件高斯分布的均值只和超参数 $\alpha _t$ 、 $x_t$ 、 $\epsilon_t$ 有关，即

${\mu}(x_t,x_0)=\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}{\epsilon_t}\right)$

方差只与超参数 $\alpha$ 有关，即

$\tilde{\beta _t} = \frac{1}{A} = 1 /\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_{t}-\bar{\alpha}_{t}+\beta_{t}}{\beta_{t}\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t}$

从而通过以上的方差和均值，我们就得到了 $q(x_{t-1}|x_t, x_0)$ 的解析形式

2.2 DDPM如何训练：通过噪声估计模型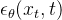 $\epsilon _\theta (x_t,t)$ 预测真实噪声——最小化估计噪声与真实噪声之间的差距

接下来介绍这个模型要怎么优化，即网络该怎么训练：去估计分布 $q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ 的条件概率 $p_\theta (x_{t-1}|x_t)$ 的均值 $u_\theta (x_t,t)$ 和方差 $\Sigma_{\theta}\left(x_{t}, \mathrm{t}\right)$

与之前介绍的VAE相比，扩散模型的隐变量是和原始数据是同维度的，而且encoder（即扩散过程）是固定的

既然扩散模型是隐变量模型，那么我们可以基于变分推断来得到variational lower bound（VLB，又称ELBO）作为最大化优化目标，当然实际训练时一般对VLB取负，即我们要最小化目标分布的负对数似然：

$\begin{aligned} -\log p_{\theta}\left(\mathbf{x}_{0}\right) & \leq-\log p_{\theta}\left(\mathbf{x}_{0}\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)\right) \\ & =-\log p_{\theta}\left(\mathbf{x}_{0}\right)+\mathbb{E}_{\mathbf{x}_{1: T} \sim q\left(\mathbf{x}_{\left.1: T \mid \mathbf{x}_{0}\right)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right) / p_{\theta}\left(\mathbf{x}_{0}\right)}\right] \\ & =-\log p_{\theta}\left(\mathbf{x}_{0}\right)+\mathbb{E}_{q}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}+\log p_{\theta}\left(\mathbf{x}_{0}\right)\right] \\ & =\mathbb{E}_{q}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}\right] \end{aligned}$

考虑到本文的定位起见，逐一解释下上面推导的每一行

第一行：由 KL 散度的非负性质（KL 散度始终大于等于零），我们得到如下不等式： $-\log p_{\theta}\left(\mathbf{x}_{0}\right) \leq-\log p_{\theta}\left(\mathbf{x}_{0}\right)+D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)\right)$

第二行：将 KL 散度的定义代入上式可得

其中 $E$ 表示期望，即对分布 $q(x_{1:T} | x_0)$ 中的所有可能值求期望

第三行：对上式进行简化，将 $-log p_{\theta }(x_0)$ 项移到期望内部

其中 $E_q$ 表示对分布 $q(x_{1:T} | x_0)$ 中的所有可能值求期望

第四行： $-log p_{\theta }(x_0)$ 和 $+log p_{\theta }(x_0)$ 相互抵消可得

令

$\text { Let } L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}\right] \geq-\mathbb{E}_{q\left(\mathbf{x}_{0}\right)} \log p_{\theta}\left(\mathbf{x}_{0}\right)$

所以 $L_{VLB}$ 就是我们的上界，我们要最小化它，接着进行变形

老规矩，上面整个推导总计九行，下面逐行解释下上面推导的每一行(纵使其他所有文章都不解释，本文也要给你解释的明明白白)

第一行，直接给出了 $L_{\mathrm{VLB}}$ 的定义，即计算概率分布 $q$ 和 $p_{\theta}$ 之间的对数比值的期望(注意，这是咱们的目标)

$L_{\mathrm{VLB}}=\mathbb{E}_{q\left(\mathbf{x}_{0: T)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}\right]$

第二行，将条件概率 $q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)$ 和联合概率 $p_{\theta}\left(\mathbf{x}_{0: T}\right)$ 展开为一系列条件概率的乘积
$q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)=\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$
考虑到 $p_{\theta}\left(\mathbf{x}_{0: T}\right)$ 实际上就是 $p_{\theta}\left(\mathbf{x}_{1: T} \mid \mathbf{x}_0\right)$ ，所以有
$p_{\theta}\left(\mathbf{x}_{0: T}\right)= p_{\theta }(x_{0}) \prod_{t=1}^{T} p_{\theta }(x_{t} | x_{0: t-1}) = p_{\theta}\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$

然后把上述结果分别分别代入 $q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)$ 和 $p_{\theta}(\mathbf{x}_{0:T})$ ，即可得到第二行的结果

$\mathbb{E}_{q}\left[\log \frac{\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right]$

第三行，将乘积转换为求和，并将 $p_\theta(\mathbf{x}_T)$ 项移到前面

$\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=1}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right]$

第四行，调整求和的范围，使其从2开始，从而达到将 $t=1$ 的项分离出来的目的

$\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right]$

第五行，将 $t$ 项的对数比值分解为两个对数比值的和，其中一个涉及 $\mathbf{x}_{t-1}$ 和 $\mathbf{x}_{t}$ ，另一个涉及 $\mathbf{x}_{t}$ 和 $\mathbf{x}_{0}$ ，相当于补了个 $x_0$

$\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)} \cdot \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}\right)+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right]$

这里得着重解释下
把第四行的第二项的分子和分母都乘以 $q(\mathbf{x}_{t-1}|\mathbf{x}_0)$ ，即得
$\log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}=\log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)} \cdot \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}\right)$

这里面的关键是，即同时乘以 $q(\mathbf{x}_{t-1}|\mathbf{x}_0)$ 后，怎么就得到上式了呢，分母部分一目了然，直接乘上的 $q(\mathbf{x}_{t-1}|\mathbf{x}_0)$ ，但分子部分呢，明明应该是 $q(x_t|x_{t-1}) q(x_{t-1}|x_0)$ ，则就变成了这个呢： $q(x_{t-1}|x_t,x_0) q(x_t|x_0)$ ？好问题! 原因在于这两个式子是等价的，即(定义为等式1)

$q(x_t|x_{t-1}) q(x_{t-1}|x_0) = q(x_{t-1}|x_t,x_0) q(x_t|x_0)$

为何等价呢，或者说上面这个等式1是怎么来的？下面再细致解释下

对于上面等式1右边的第一项 $q(x_{t-1}|x_t,x_0)$ 表示的是给定 $x_t$ 和 $x_0$ 的条件下 $x_{t-1}$ 的条件概率，因在给定 $x_0$ 的情况下， $x_t$ 和 $x_{t-1}$ 是条件独立的，根据条件概率的定义，我们可以将这个条件概率表示为联合概率与条件概率的比值，故我们有(定义为等式2)：

$q\left(x_{t-1} \mid x_{t}, x_{0}\right)=\frac{q\left(x_{t-1}, x_{t} \mid x_{0}\right)}{q\left(x_{t} \mid x_{0}\right)}$

在这个等式中，分子表示 $x_{t-1}$ 和 $x_t$ 在给定 $x_0$ 的情况下同时出现的概率，而分母表示在给定 $x_0$ 的情况下 $x_t$ 出现的概率
对于这个等式2右边项中的分子 $q(x_{t-1}, x_t \mid x_0)$ ，可以表示为(定义为等式3)：

$q\left(x_{t-1}, x_{t} \mid x_{0}\right)=q\left(x_{t} \mid x_{t-1}, x_{0}\right) q\left(x_{t-1} \mid x_{0}\right)$

由于在给定 $x_0$ 的情况下， $x_t$ 和 $x_{t-1}$ 是条件独立的，且在马尔科夫假设下，状态 $x_t$ 仅仅依赖于它的前一个状态 $x_{t-1}$ ，所以可以简化这个等式3(定义为等式4)：

$q\left(x_{t-1}, x_{t} \mid x_{0}\right)=q\left(x_{t} \mid x_{t-1}\right) q\left(x_{t-1} \mid x_{0}\right)$

现在，我们可以将上面这个等式4代入进等式2中，替换掉等式2右边项中的分子(定义为等式5)

$q\left(x_{t-1} \mid x_{t}, x_{0}\right)=\frac{q\left(x_{t} \mid x_{t-1}\right) q\left(x_{t-1} \mid x_{0}\right)}{q\left(x_{t} \mid x_{0}\right)}$

等式5右边项的分子部分等于等式右边项的分母部分乘以等式的左边项，也就得到了我们想要的这个结论：

$q(x_t|x_{t-1}) q(x_{t-1}|x_0) = q(x_{t-1}|x_t,x_0) q(x_t|x_0)$

此外，针对这个第五行，还有另外一种推法『下面五个等式先后依据：马尔科夫假设倒推、条件概率定义、分母中联合概率定义、分子中联合概率定义、分子分母同时约掉 $q(x_0)$ 』

$\begin{aligned} q\left(x_{t} \mid x_{t-1}\right) &=q\left(x_{t} \mid x_{t-1}, x_{0}\right) \\&= \frac{q\left(x_{t}, x_{t-1}, x_{0}\right)}{q\left(x_{t-1}, x_{0}\right)} \\& =\frac{q\left(x_{t-1} \mid x_{t}, x_{0}\right) q\left(x_{t} \mid x_{0}\right) q\left(x_{0}\right)}{q\left(x_{t-1}, x_{0}\right)} \\ & = \frac{q(x_{t-1}\mid x_{t},x_{0}) q(x_t\mid x_0) q(x_0)}{q(x_{t-1}\mid x_0)q(x_0)} \\ & =\frac{q\left(x_{t-1} \mid x_{t}, x_{0}\right) q\left(x_{t} \mid x_{0}\right)}{q\left(x_{t-1} \mid x_{0}\right)} \end{aligned}$

第六行，将第五行的中间项一分为二，即拆分为两个求和项

$\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right]$

第七行，将第五行中间部分得到的两个求和项的第二个求和项的最后一项 $t = T$ 分离出来，说白了，将第二个求和项的范围调整为从1到 $T-1$ ，啥意思呢
首先，第五行中间部分的两个求和项可以表示为

$\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)} = \sum_{t=2}^{T} \left[ \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)} + \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)} \right]$

接下来，关键的一步在于，上面中括号里的第二个求和项在求和过程中相邻两项会相互抵消。具体地，当 $t=k$ 时的 $q\left(\mathbf{x}_{k} \mid \mathbf{x}_{0}\right)$ 会和当 $t=k+1$ 时的 $q\left(\mathbf{x}_{k} \mid \mathbf{x}_{0}\right)$ 相互抵消。这样的抵消会发生在每一对相邻的项上，从2到 $T-1$ ，最后，只剩下 $t=T$ 和 $t=2$ 时的两项，即 $\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}$ ，从而得到最终整个第7行所示的结果，如下

$\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right]$

第八行，上一行第7行总共4项，把最后两个log项拆开成4个式子，抵消两个，还分别剩一个 $logq(x_{T}|x_0)$ 、一个 $-logp_\theta(x_0|x_1)$ ，然后 $logq(x_{T}|x_0)$ 与最初4项中的第1项 $-logp_\theta(x_T)$ 合并，即可得到整个第八行的结果

$\mathbb{E}_{q}\left[\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}-\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)\right]$

第九行，将最后一项中的负号移到对数里面，并将整个表达式重写为一系列 KL 散度项的和，这些项分别为 $L_{T}$ 、 $L_{t-1}$ 和 $L_{0}$

$\mathbb{E}_{q}[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{T}\right)\right)}_{L_{T}}+\sum_{t=2}^{T} \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\right)}_{L_{t-1}}-\underbrace{\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}_{L_{0}}]$

最后得到的表达式表示了最初我们想求解的 $L_{\mathrm{VLB}}$ 最终是一系列 KL 散度项之和，我们可以利用这个结果进行参数优化，使得两个概率分布之间的差异最小

对于上面公式最后第九行得到的结果

首先， $L_T$ 是和优化无关的(由于前向过程 q 没有可学习参数，而 $x_T$ 则是纯高斯噪声，因此 $L_T$ 可以当做常量忽略)，所以不用管，只用看右边的 $L_{t-1}$
然后， $L_{t-1}$ 是KL散度，则可以看做拉近估计分布 $p_\theta (x_{t-1}\mid x_t)$ 和真实后验分布 $q(x_{t-1}|x_t,x_0)$ 这两个分布之间的距离：
对于真实后验分布 $q(x_{t-1}|x_t,x_0)$ ，我们已经在上一节2.1.2节推导出其解析形式，这是一个高斯分布，其均值和方差为
$\tilde{\mu}_{t}=\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{t}\right)$
$\tilde{\beta}_{t}=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t}$
对于估计分布 $p_\theta (x_{t-1}\mid x_t)$ ，其是我们网络期望拟合的目标分布，也是一个高斯分布，均值用网络估计，方差被设置为了一个和 $\beta_t$ 有关的常数
$p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right), \boldsymbol{\Sigma}_{\theta}\left(\mathbf{x}_{t}, t\right)\right)$
考虑到，如果有两个分布 p,q 都是高斯分布，则他们的KL散度为
$K L(p, q)=\log \frac{\sigma_{2}}{\sigma_{1}}+\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}-\frac{1}{2}$
然后因为这两个分布的方差全是常数，和优化无关『说白了，去掉 $\sigma$ 相关的项，只留下 $(\mu _1 - \mu _2)^2$ 』，所以其实优化目标就是两个分布均值的二范数，从而可得

怎么来的？我再细致解释下，对于这个公式而言

$L_{t} =\mathbb{E}_{q}\left[\left\|\tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right]$

这里的 $\mathbb{E}_{q}$ 是在分布 $q$ 下的期望，当我们 $\tilde{\mu _t}$ 的表达式代入后，得到：
$L_{t}=\mathbb{E}_{q}\left[\left\|\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right]$

在这个式子中， $\epsilon$ 是一个服从标准正态分布的随机变量，而 $x_t$ 则取决于 $x_0$ 和 $\epsilon$ 。因此，这个期望 $\mathbb{E}_{q}$ 实际上是在 $x_0$ 和 $\epsilon$ 的联合分布下的期望(在 $x_0$ 和 $\epsilon$ 的所有可能值上取平均)，于是我们得到：
$L_{t}=\mathbb{E}_{\mathbf{x}_{0}, \epsilon}\left[\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \epsilon\right)-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}\left(\mathbf{x}_{0}, \epsilon\right), t\right)\right\|^{2}\right]$
$E_{x_0,\epsilon}$ 代表就是在 $x_0$ 和 $\epsilon$ 的联合分布下的期望， $\epsilon$ 依然是从标准正态分布 $N(0,1)$ 中采样的噪声
这个时候我们可以直接整个网络出来直接学习 $u_\theta (x_t,t)$ ，然后 $u_\theta (x_t,t)$ 再去预测

因为 $x_t$ 是 $u_\theta$ 的输入，其它的量都是常数，所以其中的未知量其实只有 $\epsilon$ ，所以我们干脆把需要学习的 $u_\theta (x_t,t)$ 定义成：
$\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right)=\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right)$
也就是说，不用网络预测 $\tilde{u_t}(x_t,x_0)$ ，而是用网络 $\epsilon _\theta (x_t,t)$ 先预测噪声 $\epsilon$ ，然后把预测出来的噪声带入到定义好的表达式中去计算出预测的均值即可
所以，最终把这个公式，代入到步骤3得到的公式中，可得：

经过这样一番推导之后就是个 L2 loss,网络的输入是一张和噪声线性组合的图片，然后要估计出来这个噪声：
$\epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \epsilon, t\right)$

由上可知，DDPM的关键是训练 $\epsilon _\theta (x_t,t)$ 模型，使其预测的 $\hat{\epsilon }$ 与真实用于破坏的 $\epsilon$ 相近，用L2距离刻画相近程度就好，因此我们的Loss就是如下公式『相当于训练时，网络输入为 $x_t$ (由 $x_0$ 和噪声 $\epsilon$ 线性组合而成) 和时刻 $t$ ，输出要尽可能的拟合输入的噪声 $\epsilon$ (通过L2 loss约束)』

而整个训练过程可如下图描述

DDPM论文中对应的伪代码为

2.3 如何通过训练好的DDPM生成图片

通过上文2.1节的最后，我们得知

从最终得到的结果可以看出，在给定 $x_0$ 的条件下

后验条件高斯分布的均值只和超参数 $\alpha _t$ 、 $x_t$ 、 $\epsilon_t$ 有关，即

${\mu}(x_t,x_0)=\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}}{\epsilon_t}\right)$

方差只与超参数 $\alpha$ 有关，即

$\tilde{\beta _t} = \frac{1}{A} = 1 /\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_{t}-\bar{\alpha}_{t}+\beta_{t}}{\beta_{t}\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \cdot \beta_{t}$

从而通过以上的方差和均值，我们就得到了 $q(x_{t-1}|x_t, x_0)$ 的解析形式

通过2.2节的最后，我们估计到了噪声估测模型 $\epsilon _\theta (x_t,t)$ ，接下来要生成模型就很简单了。从N(0,1)中随机生成一个噪声作为 $X_T$ ，然后再用该模型逐步从估测噪声，并用去噪公式逐渐恢复到 $x_0$ 即可，见如下伪代码

相当于推理时，我们从各项独立的高斯分布 $x_t$ 开始，一共 $T$ 步，每一步其实都是用了一次reparameterization trick

每一步具体来说，我们有了 $x_t$ ，想要得到 $x_{t-1}$ ，因为我们之前逆扩散过程建模有：

$p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}\left(\mathbf{x}_{t-1} ; \mu_{\theta}\left(\mathbf{x}_{t}, t\right), \Sigma_{\theta}^{2}\left(\mathbf{x}_{t}, t\right)\right)$

$=\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{\theta}\left(\mathbf{x}_{t}, t\right)\right), \beta_{t}\right)$

所以由reparameterization trick我们有：

每一轮都这样迭代，最终就得到了生成的图片

第三部分 DETR：首次通过结合CNN+Transformer端对端解决object detection

注，本小节的内容主要参考科技猛兽此文的相关部分

一般目标检测的任务是预测一系列的Bounding Box的坐标以及Label，而大多数检测器的具体做法是

要么基于proposal，比如RCNN系列的工作，类似Faster R-CNN、Mask R-CNN
要么基于anchor，比如YOLO

把问题构建成为一个分类和回归问题来间接地完成这个任务，但最后都会生成很多个预测框(确定框的坐标及框内是什么物体)，从而不可避免的出现很多冗余的框，而要去除这些冗余的框，则都需要做一个NMS(non-maximum suppersion，非极大值抑制)的后处理(使得最后调参不易、部署不易)，所以如果要是有一个端对端的模型，不需要做NMS之类的后处理也不需要太多先验知识则该有多好

而通过论文《End-to-End Object Detection with Transformers》提出的DETR则满足了大家这个期待，其取代了现在的模型需要手工设计的工作，效果不错且可扩展性强(在DETR上加个专用的分割头便可以做全景分割)，其解决的方法是把检测问题看做是一个集合预测的问题(即set prediction problem，说白了，各种预测框本质就是一个集合)，其基本流程如下图所示

CNN抽特征且拉直
全局建模，给到transformer-encoder去进一步学习全局信息
通过借助Transformer中的的self-attention机制，可以显式地对一个序列中的所有elements两两之间的interactions进行建模或交互，如此就知道了图片中哪块是哪个物体，从而对于同一个物体只需出一个预测框即可
接着通过不带掩码机制的transformer-decoder生成很多预测框
注意是并行预测(即并行出框，而不是像原始transformer预测下一个token时一个一个往外蹦)
相当于一次性生成 $N$ 个box prediction，其中 $N$ 是一个事先设定的远远大于image中object个数的一个整数(比如100)
预测框和真实框做二分图匹配
最后通过bipartite matching loss的方法，基于预测的100个boxex和ground truth boxes的二分图做匹配，计算loss的大小，从而使得预测的box的位置和类别更接近于ground truth
当然，这第4步更多是做模型训练的时候用，如果模型训练好了去做推理时，该第4步就不需要了，可以直接在预测的100个框中设定个阈值，比如置信度大于0.7的预测框保留下来，其他视为背景物体而舍弃

3.1 DETR整体结构：backbone，encoder，decoder和FFN

3.1.1 DETR结构之前两部分：backbone与encoder

更细致的讲，DETR整体结构可以分为四个部分：backbone，encoder，decoder和FFN，如下图所示

对于前两部分而言

一开始的backbone面对的是 $x_{img} \in B \times 3 \times H_0 \times W_0$ 维的图像，首先把它转换为 $f \in R^{B \times C \times H \times W}$ 维的feature map（一般来说，通道数 $C = 2048$ 或256， $H = \frac{H_0}{32}$ ， $W = \frac{W_0}{32}$ ）

然后由于encoder的输入是 $f \in R^{B \times C \times H \times W}$ 维的feature map，故正式输入encoder之前还需要依次进行以下过程(图源：科技猛兽)：

通道数压缩(其实就是降维操作)：用 1×1 convolution处理将通道数channels数量从 $C$ 压缩到 $d$ ，即得到 $z_0 \in R^{B \times d \times H \times W}$ 维的新feature map
转化为序列化数据：将空间的维度(高 $H$ 和宽 $W$ )压缩为一个维度 $HW$ ，即把上一步得到的 $z_0 \in R^{B \times d \times H \times W}$ ( $d = 256$ )维的feature map通过reshape成( $HW,B,256$ )维的feature map
这步相当于把编码矩阵的维度是 $(B,256,H,W)$ ，序列化成维度为 $(HW,B,256)$ 维的张量
位置编码：在上一步得到了 $z_0 \in R^{B \times d \times H \times W}$ 维的feature map之后，再对 $z_0 \in R^{B \times d \times H \times W}$ 维的feature map做positional encoding，最后也做下reshape：高 $H$ 和宽 $W$ 压缩为一个维度 $HW$ ，使得其与上面input embedding维度是一致的

3.1.2 详解DETR的位置编码

对于上节第三步的位置编码，再好好解释说明下
首先，通过此文《类ChatGPT逐行代码解读(1/2)：从零实现Transformer、ChatGLM-6B》的1.1.2节可知，原始transformer中的Positional Encoding的表达式为：

$PE_{(pos,2i+1)} = cos\left ( \frac{pos}{10000^{\frac{2i}{d_{model}}}} \right )$

$PE_{(pos,2i)} = sin\left ( \frac{pos}{10000^{\frac{2i}{d_{model}}}} \right )$

其中， $d$ 就是这个 $d \times HW$ 维的feature map的第一维， $pos \in [1,HW]$ 表示token在sequence中的位置，sequence的长度是 $HW$ ，例如第一个token 的 $pos = 0$ ，第二个token的 $pos = 1$
$i$ ，或者准确意义上是 $2i$ 和 $2i+1$ 表示了Positional Encoding的维度， $i$ 的取值范围是： $[0,...,d_{model}/2]$ ，所以当 $pos$ 为1时，对应的Positional Encoding可以写成(注意到 $d = 256$ )：

$PE_1 = [sin(\frac{1}{10000^{\frac{0}{256}}}),cos(\frac{1}{10000^{\frac{0}{256}}}), sin(\frac{1}{10000^{\frac{2}{256}}}),cos(\frac{1}{10000^{\frac{2}{256}}}), sin(\frac{1}{10000^{\frac{4}{256}}}), cos(\frac{1}{10000^{\frac{4}{256}}}),..., sin(\frac{1}{10000^{\frac{255}{256}}}),cos(\frac{1}{10000^{\frac{255}{256}}})]$

其次，DETR与原版transformer中的位置编码有两点不同

第一点不同的是，原版Transformer只考虑 $x$ 方向的位置编码，但是DETR考虑了 $xy$ 方向的位置编码，因为图像特征是2-D特征。采用的依然是 sin cos 模式，但是需要考虑 $xy$ 两个方向。不是类似vision transoformer做法简单的将其拉伸为 $d \times HW$ ，然后从 $[1,HW]$ 进行长度为256的位置编码，而是考虑了 $xy$ 方向同时编码，每个方向各编码128维向量，这种编码方式更符合图像特点

Positional Encoding的输出张量是： $(B,d,H,W)$ , $d = 256$ ，其中 $d$ 代表位置编码的长度， $H,W$ 代表张量的位置。意思是说，这个特征图上的任意一个点 $(H_1,W_1)$ 有个位置编码，这个编码的长度是256，其中，前128维代表 $H_1$ 的位置编码，后128维代表 $W_1$ 的位置编码

$a) P E_{\left(p_{x}, 2 i\right)}=\sin \left(\operatorname{pos}_{x} / 10000^{2 i / 128}\right) \\\ b) P E_{\left(p_{0}, 2 i+1\right)}=\cos \left(\operatorname{pos}_{x} / 10000^{2 i / 128}\right) \\c) P E_{\left(p o s_{y}, 2 i\right)}=\sin \left(\operatorname{pos}_{y} / 10000^{2 i / 128}\right) \\ d) P E_{\left(p o s_{y}, 2 i+1\right)}=\cos \left(\operatorname{pos}_{y} / 10000^{2 i / 128}\right)$

假设你想计算任意一个位置 $(pos_x,pos_y)$ ， $pos_x \in[1,HW]$ ， $pos_y \in[1,HW]$ 的Positional Encoding
$\rightarrow$ 先把 $pos_x$ 代入上面4个公式中的 $a$ 式和 $b$ 式可以计算得到128维的向量，它代表 $pos_x$ 的位置编码
$\rightarrow$ 再把 $pos_y$ 代入上面4个公式中的 $c$ 式和 $d$ 式可以计算得到128维的向量，它代表 $pos_y$ 的位置编码
$\rightarrow$ 把这2个128维的向量拼接起来，就得到了一个256维的向量，它代表 $(pos_x,pos_y)$ 的位置编码
从而计算所有位置的编码，就得到了 $(256,H,W)$ 的张量，代表这个batch的位置编码
第二点不同的是，原版Transformer只在Encoder之前使用了Positional Encoding，而且是在输入上进行Positional Encoding，再把输入经过transformation matrix变为Query，Key和Value这几个张量
但是DETR在Encoder的每一个Multi-head Self-attention之前都使用了Positional Encoding，且只对Query和Key使用了Positional Encoding，即：只把维度为 $(HW,B,256)$ 维的位置编码与维度为 $(HW,B,256)$ 维的Query和Key相加，而不与Value相加

下图为DETR的Transformer的详细结构，读者可以对比下原版Transformer的结构可以发现，除了Positional Encoding设置的不一样外，Encoder其他的结构是一致的。每个Encoder Layer包含一个multi-head self-attention 的module和一个前馈网络Feed Forward Network

所以，了解了DETR的位置编码之后，你应该明白了其实input embedding和位置编码维度其实是一样的，从而也就可以直接相加，使得Encoder最终输出的是 $(HW,b,256)$ 维的编码矩阵Embedding，按照原版Transformer的做法，把这个东西给Decoder

3.1.3 DETR结构的后两部分：decoder和FFN

通过上节最后的对比图，可知DETR的Decoder和原版Transformer的decoder也是不太一样的

对于原版Transformer，其decoder的最后一个框(上节最后对比图的左图右上角所示)：output probability，代表我们一次只产生一个单词的softmax，根据这个softmax得到这个单词的预测结果，即：predicts the output sequence one element at a time
不同的是，DETR的Transformer Decoder是一次性处理全部的object queries(上节最后对比图的右图右上角所示)，即一次性输出全部的predictions(而不像原始的Transformer是auto-regressive的，从左到右一个词一个词地输出)，即：decodes the N objects in parallel at each decoder layer

至于DETR的Decoder主要有两个输入：

第一个输入是Transformer Encoder输出的Embedding与 position encoding(在下图右侧第二个multi-head self-attention处)相加之后给到 $K$
其中的Embedding就是上文提到的 $(HW,B,256)$ 的编码矩阵
第二个输入是Object queries
所谓Object queries是一个维度为 $(100,b,256)$ 维的张量，数值类型是nn.Embedding(意味着是可以学习的)。Object queries矩阵内部通过学习建模了100个物体之间的全局关系，例如房间里面的桌子旁边(A类)一般是放椅子(B类)，而不会是放一头大象(C类)，那么在推理时候就可以利用该全局注意力更好的进行解码预测输出

关于上图右侧第1个multi-head self-attention的Q K V
如上图所示，它的Q K是这么来的：Decoder原本的输入一开始初始化成维度为 $(100,b,256)$ 维的全部元素都为0的张量，然后和Object queries加在一起之后充当第1个multi-head self-attention的Query和Key，至于Value则是Decoder原本的输入，也就是全0的张量

关于上图右侧第2个multi-head self-attention的Q K V
它的Key和Value来自Encoder的输出张量，维度为 $(hw,b,256)$ ，其中Key值还进行位置编码(正如上面第一个输入所述)
至于其Query值一部分来自第1个Add and Norm的输出，维度为 $(100,b,256)$ 的张量，另一部分来自Object queries，充当可学习的位置编码
所以，第2个multi-head self-attention的Key和Value的维度为 $(hw,b,256)$ ，而Query的维度为 $(100,b,256)$

每个Decoder的输出维度为 $(1,b,100,256)$ ，送入后面的前馈网络

到这里你会发现：Object queries充当的其实是位置编码的作用，只不过它是可以学习的位置编码，所以，我们对Encoder和Decoder的每个self-attention的Query和Key的位置编码做个归纳，如下图所示，Value没有位置编码

3.1.4损失函数部分解读

得到了Decoder的输出以后，如前文所述，应该是输出维度为 $(b,100,256)$ 的张量。接下来要送入2个前馈网络FFN得到class和Bounding Box(如再度引用的下图所示)，它们会得到 $N=100$ 个预测目标包含类别和Bounding Box(当然这个100肯定是大于图中的目标总数的，如果不够100，则采用背景填充

所以，DETR输出张量的维度为 $(b,100,class+1)$ ，和 $(b,100,4)$ 『对应COCO数据集来说： $class+1=92$ ， 4 指的是每个预测目标归一化的 $(c_x,c_y,w,h)$ ，归一化就是除以图片宽高进行归一化』，对于这两个维度

前者代表分类分支，指100个预测框的类型
后者代表回归分支，指100个预测框的Bounding Box(仅仅计算有物体位置，背景集合忽略)

但是读者可能会有疑问：预测框和真值是怎么一一对应的？换句话说：你怎么知道第47个预测框对应图片里的狗，第88个预测框对应图片里的车？..

这就需要用到经典的双边匹配算法了，也就是常说的匈牙利算法，该算法广泛应用于最优分配问题
一幅图片，我们把第 $i$ 个物体的真值表达为 $y_i = (c_i,b_i)$ ，其中， $c_i$ 表示它的 class ， $b_i$ 表示它的 Bounding Box
然后定义 $\hat{y}=\left\{\hat{y}_{i}\right\}_{i=1}^{N}$ 为网络输出的 $N$ 个预测值
对于第 $i$ 个真值 $GT$ ， $\sigma (i)$ 为匈牙利算法得到的与真值 $GT_i$ 对应的预测值prediction的索引，举个例子，比如 $i = 3$ ， $\sigma (i) = 18$ ，意思就是：与第3个真值对应的预测值是第18个
那如何根据匈牙利算法找到与每个真值对应的预测值到底是哪个呢？
$\hat{\sigma}=\arg \min _{\sigma \in \Sigma_{N}} \sum_{i}^{N} L_{\text {match }}\left(y_{i}, \hat{y}_{\sigma(i)}\right)$

对于某一个真值 $y_i$ ，假设已经找到这个真值对应的预测值 $\hat{y}_{\sigma (i)}$ ，这里的 $\Sigma _N$ 是所有可能的排列(代表从真值索引到预测值索引的所有的映射)，然后用 $L_{match}$ 最小化 $y_i$ 和 $\hat{y}_{\sigma (i)}$ 的距离
这个 $L_{match}$ 具体是：
$-1_{\left\{c_{i} \neq \varnothing\right\}} \hat{p}_{\sigma(i)}\left(c_{i}\right)+1_{\left\{c_{i} \neq \varnothing\right\}} L_{b o x}\left(b_{i}, \hat{b}_{\sigma(i)}\right)$

意思是：假设当前从真值索引到预测值索引的所有映射为 $\sigma$ ，对于图片中的每个真值 $i$
$\rightarrow$ 先找到对应的预测值 $\sigma (i)$ ，再看看分类网络的结果 $\hat{p}_{\sigma(i)}\left(c_{i}\right)$ ，取反作为 $L_{match}$ 的第1部分
$\rightarrow$ 再计算回归网络的结果 $\hat{b}_{\sigma(i)}$ 与真值的 Bounding Box 的差异，即 $L_{b o x}\left(b_{i}, \hat{b}_{\sigma(i)}\right)$ ，作为 $L_{match}$ 的第2部分
所以，可以使得 $L_{match}$ 最小的排列 $\hat{\sigma }$ 就是我们要找的排列，即：对于图片中的每个真值 $i$ 来讲， $\hat{\sigma}(i)$ 就是这个真值所对应的预测值的索引
上述这个匈牙利算法的过程与Anchor或Proposal有异曲同工的地方，只是此时我们找的是一对一匹配
接下来就是使用上一步得到的排列 $\hat{\sigma }$ ，计算匈牙利损失
$L_{\text {Hungarian }}(y, \hat{y})=\sum_{i=1}^{N}\left[-\log \hat{p}_{\hat{\sigma}(i)}\left(c_{i}\right)+1_{\left\{c_{i} \neq \varnothing\right\}} L_{b o x}\left(b_{i}, \hat{b}_{\hat{\sigma}(i)}\right)\right]$
式中的 $L_{box}$ 具体为：

最常用的 $L_1$ loss对于大小 Bounding Box 会有不同的标度，即使它们的相对误差是相似的。为了缓解这个问题，作者使用了 $L_1$ loss和广义IoU损耗 $L_{iou}$ 的线性组合，它是比例不变的
Hungarian意思就是匈牙利，也就是前面的 $L_{match}$ ，上述意思是需要计算 $M$ 个 GTBounding Box 和 $N$ 个输预测出集合两两之间的广义距离，距离越近表示越可能是最优匹配关系，也就是两者最密切，广义距离的计算考虑了分类分支和回归分支

第四部分 ViT到SwinTransformer

//待更..

参考文献与推荐阅读

变分自编码器（一）：原来是这么一回事
..
关于VAE的几篇文章：一文理解变分自编码器（VAE）、机器学习方法—优雅的模型（一）：变分自编码器（VAE）、
苏剑林关于扩散模型的几篇文章：（一）：DDPM = 拆楼 + 建楼、（二）：DDPM = 自回归式VAE
怎么理解今年 CV 比较火的扩散模型（DDPM）？
知乎上关于扩散模型的几篇文章：全网最简单的扩散模型DDPM教程、Diffusion扩散模型大白话讲解、扩散生成模型: 唯美联姻物理概念与机器学习
Understanding Diffusion Models: A Unified Perspective(写于2022年8月，此文写的非常细致，另，这是其PDF版本)
扩散模型是如何工作的：从0开始的数学原理
What are Diffusion Models?，写于2021年7月
Introduction to Diffusion Models for Machine Learning
关于扩散模型的几篇论文
CVPR 2022 Tutorial: Denoising Diffusion-based Generative Modeling: Foundations and Applications
Diffusion Models Beat GANs on Image Synthesis
关于DDPM的几篇文章(如果相关文章与本文有冲突，建议以本文为准，因为有些文章有笔误或错误)：DDPM概率扩散模型（原理+代码)、Denoising Diffusion Probabilistic Models (DDPM)、从VAE到DDPM、扩散模型原理解析
Vision Transformer 超详细解读 (原理分析+代码解读) (一)
DETR论文的解读之一
End-to-End Object Detection with Transformers，DETR原始论文

创作、修改/完善记录

第一大阶段
4.28，因要发布AI绘画与CV多模态原理解析的博客，从VAE开始写起
反复理了一个下午，总算把VAE写清楚了，也看了很多同类文章，之前推导看不下去的都能看得下去了
5.1，拆解DDPM的前向过程，其他同类文章对于一个公式可能一步或两三步到位我而言，能拆10步则10步阅读无障碍，不然何必我来写
5.3，连续抠了两天DDPM的推导总算有雏形了
5.4，今天又抠了一天的DDPM公式推导，增加了很多同类文章里没有的细节，很爽这就是我提笔的价值和意义所在了
5.6，完善2.2节
从5.2日起，连抠了整整4天DDPM的前向逆向推导，总算快写清楚了整个推导过程
大家害怕的不是公式，只是怕公式的展开不够细致，毕竟对每一个人而言，公式展开越细致越不怕

且解读 $L_{VLB}$ 九行推导的每一行
解读代码时对每一行代码都加注释
拆解公式时对每一行公式都做解释

已是一个固定的风格，这样人人都能理解
5.10，继续完善2.2节
理解DDPM不难，但里面的公式推导特别多，为了让每位朋友可以一目了然的理解每一个公式的推导
只要能拆开的一定拆开要解释的一定解释
5.12，再次完善2.1.2节逆向过程(去噪)
为让整个推导看下来不费劲，修改部分描述以更流畅，使得最终尽可能就像看小说一样
5.14，开始更新3.1节DETR的部分
5.15，修改完善3.1节DETR结构之前两部分：backbone与encoder
5.16，开始更新3.1节DETR结构的后两部分：decoder和FFN，以及损失函数部分解读
第二大阶段
5.19，修改完善3.1节3.1节DETR结构的后两部分：decoder和FFN，以及损失函数部分解读
尽可能让行文清晰直观一目了然避免看着费劲/别扭

AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、DETR、ViT/Swin transformer相关推荐

LDA通俗理解LDA主题模型
转自:http://blog.csdn.net/v_july_v/article/details/41209515#t13 通俗理解LDA主题模型 0 前言印象中,最开始听说"LDA&qu ...
通俗理解LDA主题模型(转载自 v_JULY_v 大佬)
通俗理解LDA主题模型原文:https://blog.csdn.net/v_july_v/article/details/41209515 0 前言印象中,最开始听说"LDA" ...
通俗理解LDA主题模型（转）
from :http://blog.csdn.net/v_july_v/article/details/41209515 也推荐:LDA漫步指南通俗理解LDA主题模型 0 前言印象中,最开始听说& ...
李沐论文精读系列五：DALL·E2（生成模型串讲，从GANs、VE/VAE/VQ-VAE/DALL·E到扩散模型DDPM/ADM）
文章目录一. 前言 1.1 DALL·E简介 1.2 DALL·E2简介 1.3 文生图模型进展二. 引言 2.1 摘要 2.2 引言&模型结构三. 算法铺垫 3.1 GANs 3.2 ...
AI绘画最强工具：集成所有国内外主流大模型AI绘画能力文生图、图生图、图修复和超分辨率能力。
AIGC(Artificial Intelligence Generated Content)登上舞台,以高效.精准.定制化等能力特征,重新定义了内容生产方式. 只需通过4行代码就能实现强大的文图生成 ...
通俗理解LDA主题模型
0 前言印象中,最开始听说"LDA"这个名词,是缘于rickjin在2013年3月写的一个LDA科普系列,叫LDA数学八卦,我当时一直想看来着,记得还打印过一次,但不知是因为这篇 ...
NLP系列笔记：通俗理解LDA主题模型
0 前言印象中,最开始听说"LDA"这个名词,是缘于rickjin在2013年3月写的一个LDA科普系列,叫LDA数学八卦,我当时一直想看来着,记得还打印过一次,但不知是 ...
人工智能 AI 绘画发展史
到了去年4月, 著名人工智能团队OpenAI 也发布了新模型 DALL·E 2代,该名称来源于著名画家达利(Dalí)和机器人总动员(Wall-E), 同样支持从文本描述生成效果良好的图像. 而很多读 ...
【分布式】分布式深度学习DDLs系统Review——分布式学习通俗理解Distributed Deep Learning Systems（最全面的论述）
分布式深度学习系统 (DDLS) 通过利用集群的分布式资源来训练深度神经网络模型. DDLS 的开发人员需要做出许多决定,以在他们选择的环境中有效地处理他们的特定工作负载. 基于 GPU 的深度学习的 ...

AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、DETR、ViT/Swin transformer

前言

第一部分编码器VE与变分自编码器VAE

1.1 AE：编码器(数据 $X$ 压缩为低维表示 $z$ )-解码器(低维表示恢复为原始数据 $\hat{X}$ )架构

1.2 Variational AutoEncoder (VAE)

1.2.1 VAE：标数据的分布 $\hat{X}$ 和目标分布 $X$ 尽量接近

1.2.2 VAE的Variational到底是个啥

第二部分扩散模型DDPM：先前向加噪后反向去噪从而建立噪声估计模型

2.1 DDPM的两个过程：从前向过程到逆向过程

2.1.1 前向过程(加噪)：通过高斯噪音随机加噪 $\epsilon$ ——给图片打马赛克

2.1.2 逆向过程(去噪)：求解真实后验分布 $q(x_{t-1}|x_t, x_0)$ —— 复原被加噪的图片使之清晰化

2.2 DDPM如何训练：通过噪声估计模型 $\epsilon _\theta (x_t,t)$ 预测真实噪声——最小化估计噪声与真实噪声之间的差距

2.3 如何通过训练好的DDPM生成图片

第三部分 DETR：首次通过结合CNN+Transformer端对端解决object detection

3.1 DETR整体结构：backbone，encoder，decoder和FFN

3.1.1 DETR结构之前两部分：backbone与encoder

3.1.2 详解DETR的位置编码

3.1.3 DETR结构的后两部分：decoder和FFN

3.1.4损失函数部分解读

第四部分 ViT到SwinTransformer

参考文献与推荐阅读

创作、修改/完善记录

AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、DETR、ViT/Swin transformer相关推荐

最新文章

热门文章

AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、DETR、ViT/Swin transformer

前言

第一部分 编码器VE与变分自编码器VAE

1.1 AE：编码器(数据压缩为低维表示)-解码器(低维表示恢复为原始数据)架构

1.2 Variational AutoEncoder (VAE)

1.2.1 VAE：标数据的分布和目标分布尽量接近

1.2.2 VAE的Variational到底是个啥

第二部分 扩散模型DDPM：先前向加噪后反向去噪从而建立噪声估计模型

2.1 DDPM的两个过程：从前向过程到逆向过程

2.1.1 前向过程(加噪)：通过高斯噪音随机加噪 ——给图片打马赛克

2.1.2 逆向过程(去噪)：求解真实后验分布—— 复原被加噪的图片使之清晰化

2.2 DDPM如何训练：通过噪声估计模型预测真实噪声——最小化估计噪声与真实噪声之间的差距

2.3 如何通过训练好的DDPM生成图片

第三部分 DETR：首次通过结合CNN+Transformer端对端解决object detection

3.1 DETR整体结构：backbone，encoder，decoder和FFN

3.1.1 DETR结构之前两部分：backbone与encoder

3.1.2 详解DETR的位置编码

3.1.3 DETR结构的后两部分：decoder和FFN

3.1.4损失函数部分解读

第四部分 ViT到SwinTransformer

参考文献与推荐阅读

创作、修改/完善记录

AI绘画能力的起源：通俗理解VAE、扩散模型DDPM、DETR、ViT/Swin transformer相关推荐

最新文章

热门文章

第一部分编码器VE与变分自编码器VAE

1.1 AE：编码器(数据 $X$ 压缩为低维表示 $z$ )-解码器(低维表示恢复为原始数据 $\hat{X}$ )架构

1.2.1 VAE：标数据的分布 $\hat{X}$ 和目标分布 $X$ 尽量接近

第二部分扩散模型DDPM：先前向加噪后反向去噪从而建立噪声估计模型

2.1.1 前向过程(加噪)：通过高斯噪音随机加噪 $\epsilon$ ——给图片打马赛克

2.1.2 逆向过程(去噪)：求解真实后验分布 $q(x_{t-1}|x_t, x_0)$ —— 复原被加噪的图片使之清晰化

2.2 DDPM如何训练：通过噪声估计模型 $\epsilon _\theta (x_t,t)$ 预测真实噪声——最小化估计噪声与真实噪声之间的差距