Floyd-Warshall算法，简称Floyd算法，用于求解任意两点间的最短距离，时间复杂度为O(n^3)。我们平时所见的Floyd算法的一般形式如下：

1  void  Floyd(){
2       int  i,j,k;
3       for (k = 1 ;k <= n;k ++ )
4           for (i = 1 ;i <= n;i ++ )
5               for (j = 1 ;j <= n;j ++ )
6                   if (dist[i][k] + dist[k][j] < dist[i][j])
7                      dist[i][j] = dist[i][k] + dist[k][j];
8  }

注意下第6行这个地方，如果dist[i][k]或者dist[k][j]不存在，程序中用一个很大的数代替。最好写成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j])，从而防止溢出所造成的错误。
  上面这个形式的算法其实是Floyd算法的精简版，而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。
  设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度，其中k 表示该路径中的最大顶点，也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此，如果G中包含边<i, j>，则c[i, j, 0] =边<i, j> 的长度；若i= j ，则c[i,j,0]=0；如果G中不包含边<i, j>，则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。
  对于任意的k>0，通过分析可以得到：中间顶点不超过k 的i 到j 的最短路径有两种可能：该路径含或不含中间顶点k。若不含，则该路径长度应为c[i, j, k-1]，否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。
  状态转移方程：c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]}，k＞0。
  这样，问题便具有了最优子结构性质，可以用动态规划方法来求解。

为了进一步理解，观察上面这个有向图：若k=0, 1, 2, 3，则c[1,3,k]= +∞；c[1,3,4]= 28；若k = 5, 6, 7，则c [1,3,k] = 10；若k=8, 9, 10，则c[1,3,k] = 9。因此1到3的最短路径长度为9。
  下面通过程序来分析这一DP过程，对应上面给出的有向图：

 1  #include  < iostream >
 2  using   namespace  std;
 3 
 4  const   int  INF  =   100000 ;
 5  int  n = 10 ,map[ 11 ][ 11 ],dist[ 11 ][ 11 ][ 11 ];
 6  void  init(){
 7       int  i,j;
 8       for (i = 1 ;i <= n;i ++ )
 9           for (j = 1 ;j <= n;j ++ )
10              map[i][j] = (i == j) ? 0 :INF;
11      map[ 1 ][ 2 ] = 2 ,map[ 1 ][ 4 ] = 20 ,map[ 2 ][ 5 ] = 1 ;
12      map[ 3 ][ 1 ] = 3 ,map[ 4 ][ 3 ] = 8 ,map[ 4 ][ 6 ] = 6 ;
13      map[ 4 ][ 7 ] = 4 ,map[ 5 ][ 3 ] = 7 ,map[ 5 ][ 8 ] = 3 ;
14      map[ 6 ][ 3 ] = 1 ,map[ 7 ][ 8 ] = 1 ,map[ 8 ][ 6 ] = 2 ;
15      map[ 8 ][ 10 ] = 2 ,map[ 9 ][ 7 ] = 2 ,map[ 10 ][ 9 ] = 1 ;
16  }
17  void  floyd_dp(){
18       int  i,j,k;
19       for (i = 1 ;i <= n;i ++ )
20           for (j = 1 ;j <= n;j ++ )
21              dist[i][j][ 0 ] = map[i][j];
22       for (k = 1 ;k <= n;k ++ )
23           for (i = 1 ;i <= n;i ++ )
24               for (j = 1 ;j <= n;j ++ ){
25                  dist[i][j][k] = dist[i][j][k - 1 ];
26                   if (dist[i][k][k - 1 ] + dist[k][j][k - 1 ] < dist[i][j][k])
27                      dist[i][j][k] = dist[i][k][k - 1 ] + dist[k][j][k - 1 ];
28              }
29  }
30  int  main(){
31       int  k,u,v;
32      init();
33      floyd_dp();
34       while (cin >> u >> v,u || v){
35           for (k = 0 ;k <= n;k ++ ){
36               if (dist[u][v][k] == INF) cout << " +∞ " << endl;
37               else  cout << dist[u][v][k] << endl;
38          }
39      }
40       return   0 ;
41  }

输入 1 3
  输出 +∞
            +∞
            +∞
            +∞
            28
            10
            10
            10
            9
            9
            9

Floyd-Warshall算法不仅能求出任意2点间的最短路径，还可以保存最短路径上经过的节点。下面用精简版的Floyd算法实现这一过程，程序中的图依然对应上面的有向图。

 1  #include  < iostream >
 2  using   namespace  std;
 3 
 4  const   int  INF  =   100000 ;
 5  int  n = 10 ,path[ 11 ][ 11 ],dist[ 11 ][ 11 ],map[ 11 ][ 11 ];
 6  void  init(){
 7       int  i,j;
 8       for (i = 1 ;i <= n;i ++ )
 9           for (j = 1 ;j <= n;j ++ )
10              map[i][j] = (i == j) ? 0 :INF;
11      map[ 1 ][ 2 ] = 2 ,map[ 1 ][ 4 ] = 20 ,map[ 2 ][ 5 ] = 1 ;
12      map[ 3 ][ 1 ] = 3 ,map[ 4 ][ 3 ] = 8 ,map[ 4 ][ 6 ] = 6 ;
13      map[ 4 ][ 7 ] = 4 ,map[ 5 ][ 3 ] = 7 ,map[ 5 ][ 8 ] = 3 ;
14      map[ 6 ][ 3 ] = 1 ,map[ 7 ][ 8 ] = 1 ,map[ 8 ][ 6 ] = 2 ;
15      map[ 8 ][ 10 ] = 2 ,map[ 9 ][ 7 ] = 2 ,map[ 10 ][ 9 ] = 1 ;
16  }
17  void  floyd(){
18       int  i,j,k;
19       for (i = 1 ;i <= n;i ++ )
20           for (j = 1 ;j <= n;j ++ )
21              dist[i][j] = map[i][j],path[i][j] = 0 ;
22       for (k = 1 ;k <= n;k ++ )
23           for (i = 1 ;i <= n;i ++ )
24               for (j = 1 ;j <= n;j ++ )
25                   if (dist[i][k] + dist[k][j] < dist[i][j])
26                      dist[i][j] = dist[i][k] + dist[k][j],path[i][j] = k;
27  }
28  void  output( int  i, int  j){
29       if (i == j)  return ;
30       if (path[i][j] == 0 ) cout << j << '   ' ;
31       else {
32          output(i,path[i][j]);
33          output(path[i][j],j);
34      }
35  }
36  int  main(){
37       int  u,v;
38      init();
39      floyd();
40       while (cin >> u >> v,u || v){
41           if (dist[u][v] == INF) cout << " No path " << endl;
42           else {
43              cout << u << '   ' ;
44              output(u,v);
45              cout << endl;
46          }
47      }
48       return   0 ;
49  }

输入 1 3                    
  输出 1 2 5 8 6 3

floyd算法

弗洛伊德（Floyd）算法过程：
１、用D[v][w]记录每一对顶点的最短距离。
２、依次扫描每一个点，并以其为基点再遍历所有每一对顶点D[][]的值，看看是否可用过该基点让这对顶点间的距离更小。

算法理解：
最短距离有三种情况：
１、两点的直达距离最短。（如下图<v,x>）
２、两点间只通过一个中间点而距离最短。（图<v,u>）
３、两点间用通过两各以上的顶点而距离最短。（图<v,w>）

对于第一种情况：在初始化的时候就已经找出来了且以后也不会更改到。
对于第二种情况：弗洛伊德算法的基本操作就是对于每一对顶点，遍历所有其它顶点，看看可否通过这一个顶点让这对顶点距离更短，也就是遍历了图中所有的三角形（算法中对同一个三角形扫描了九次，原则上只用扫描三次即可，但要加入判断，效率更低）。
对于第三种情况：如下图的五边形，可先找一点（比如x，使<v,u>=2），就变成了四边形问题，再找一点（比如y,使<u,w>=2），可变成三角形问题了（v,u,w），也就变成第二种情况了，由此对于n边形也可以一步步转化成四边形三角形问题。（这里面不用担心哪个点要先找哪个点要后找，因为找了任一个点都可以使其变成（n－1）边形的问题）。

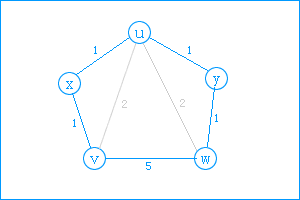
floyd的核心代码:

for  (k = 0 ;k < g.vexnum;k ++ )
{
     for  (i = 0 ;i < g.vexnum;i ++ )
    {
         for  (j = 0 ;j < g.vexnum;j ++ )
        {
             if  (distance[i][j] > distance[i][k] + distance[k][j])
            {
                distance[i][j] = distance[i][k] + distance[k][j];
            }
        }
    }
}

结合代码 并参照上图所示 我们来模拟执行下 这样才能加深理解：
第一关键步骤：当k执行到x，i=v,j=u时，计算出v到u的最短路径要通过x，此时v、u联通了。
第二关键步骤：当k执行到u，i=v，j=y，此时计算出v到y的最短路径的最短路径为v到u，再到y(此时v到u的最短路径上一步我们已经计算过来，直接利用上步结果)。
第三关键步骤：当k执行到y时，i=v，j=w，此时计算出最短路径为v到y(此时v到y的最短路径长在第二步我们已经计算出来了)，再从y到w。

依次扫描每一点(k)，并以该点作为中介点，计算出通过k点的其他任意两点(i,j)的最短距离，这就是floyd算法的精髓！同时也解释了为什么k点这个中介点要放在最外层循环的原因.

// 多源最短路径,floyd_warshall算法,复杂度O(n^3)
// 求出所有点对之间的最短路经,传入图的大小和邻接阵
// 返回各点间最短距离min[]和路径pre[],pre[i][j]记录i到j最短路径上j的父结点
// 可更改路权类型,路权必须非负!
#define  MAXN 200
#define  inf 1000000000
typedef  int  elem_t;

void  floyd_warshall( int  n,elem_t mat[][MAXN],elem_t min[][MAXN], int  pre[][MAXN]){
     int  i,j,k;
     for  (i = 0 ;i < n;i ++ )
         for  (j = 0 ;j < n;j ++ )
            min[i][j] = mat[i][j],pre[i][j] = (i == j) ?- 1 :i;
     for  (k = 0 ;k < n;k ++ )
         for  (i = 0 ;i < n;i ++ )
             for  (j = 0 ;j < n;j ++ )
                 if  (min[i][k] + min[k][j] < min[i][j])
                    min[i][j] = min[i][k] + min[k][j],pre[i][j] = pre[k][j];
}

Floyd-Warshall算法详解（转）相关推荐

  1. O-矩阵相乘-Warshall算法详解

    给出2个N * N的矩阵M1和M2,输出2个矩阵相乘后的结果. Input第1行:1个数N,表示矩阵的大小(2 <= N <= 100)  第2 - N + 1行,每行N个数,对应M1的1 ...

  2. Floyed（floyd）算法详解

    是真懂还是假懂? Floyed算法:是最短路径算法可以说是最慢的一个. 原理:O(n^3)的for循环,对每一个中间节点k做松弛(寻找更短路径): 但它适合算多源最短路径,即任意两点间的距离. 但sp ...

  3. 【最短路径Floyd算法详解推导过程】看完这篇，你还能不懂Floyd算法？还不会？...

    简介 Floyd-Warshall算法(Floyd-Warshall algorithm),是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似.该算法名称以 ...

  4. 最短路径问题---Floyd算法详解

    前言 Genius only means hard-working all one's life. Name:Willam Time:2017/3/8 1.最短路径问题介绍 问题解释: 从图中的某个顶 ...

  5. 排序算法(五)——堆排序算法详解及Python实现

    本文目录 一.简介 二.算法介绍 三.代码实现 排序算法系列--相关文章 一.简介 堆排序(Heap Sort)算法,属于选择排序类,不稳定排序,时间复杂度O(nlogn). 堆排序由Floyd和Wi ...

  6. Dijkstra算法详解（完美图解、趣学算法）

    Dijkstra算法详解 Dijkstra算法设计 Dijkstra算法简介 Dijkstra算法的基本思想 Dijkstra贪心策略 完美图解 伪代码详解 完整代码 算法解析及优化拓展 使用优先队列 ...

  7. Matlab人脸检测算法详解

    这是一个Matlab人脸检测算法详解 前言 人脸检测结果 算法详解 源代码解析 所调用函数解析 bwlabel(BW,n) regionprops rectangle 总结 前言 目前主流的人脸检测与 ...

  8. 图论-最短路Dijkstra算法详解超详 有图解

    整体来看dij就是从起点开始扩散致整个图的过程,为什么说他稳定呢,是因为他每次迭代,都能得到至少一个结点的最短路.(不像SPFA,玄学复杂度) 但是他的缺点就是不能处理带负权值的边,和代码量稍稍复杂. ...

  9. C++中的STL算法详解

    1.STL算法详解 STL提供能在各种容器中通用的算法(大约有70种),如插入.删除.查找.排序等.算法就是函数模板,算法通过迭代器来操纵容器中的元素.许多算法操作的是容器上的一个区间(也可以是整个容 ...

  10. 粒子群(pso)算法详解matlab代码,粒子群(pso)算法详解matlab代码

    粒子群(pso)算法详解matlab代码 (1)---- 一.粒子群算法的历史 粒子群算法源于复杂适应系统(Complex Adaptive System,CAS).CAS理论于1994年正式提出,C ...

最新文章

  1. Loj #6287 诗歌
  2. 设计原则——依赖倒置
  3. linux下的c编程
  4. 源代码管理工具优缺点
  5. python微信跳一跳小游戏刷分
  6. Windows Azure 将正式更名为 Microsoft Azure
  7. Redis 2.8.9源码 - Redis中的字符串实现 sds
  8. 软件开发中的需求种类
  9. pygame安装教程
  10. 小工具 | 全站仪图根测量平差excel计算表格
  11. 基于docker搭开源iredmail邮箱服务器
  12. LeetCode 714. 买卖股票的最佳时机含手续费
  13. 系统分析师学习笔记（十七）
  14. 北京邮电计算机相关知识,2019北京邮电大学计算机专业考研经验分享
  15. 驾考通-小型汽车考试
  16. MATLAB之多项式插值
  17. 将两个各有n个元素的有序表归并成一个有序表,其最多的比较次数
  18. gpu超算算法_GPU: 超算加速
  19. MindMapper 与MindManager之间的区别
  20. CSS基础（12）- 定位

热门文章

  1. 最优秀好用的免费文件压缩/解压缩工具软件 (可替代WinRAR与7-Zip)——Bandizip
  2. Sam Altman 山姆奥特曼：How To Invest In Startups如何投资初创公司
  3. String类型的测量长度
  4. 苹果弃妇效应再现:Audience一夜跌去63%(转)
  5. 与智能汽车相见恨晚的SOA到底是什么？
  6. 电影《美丽心灵》中纳什的经典演讲（双语）
  7. 【Spark NLP】第 7 章：分类和回归
  8. 【机器视觉】Halcon 19安装教程详解
  9. 最好看的Excel条形图 如何用Excel图表把它做出来
  10. 解决：Excel打开文件，内容不显示