JuMP: 用Julia进行优化建模及求解- 覃含章的文章 - 知乎 https://zhuanlan.zhihu.com/p/40807662

JuMP: 用Julia进行优化建模及求解 - 覃含章的文章 - 知乎 https://zhuanlan.zhihu.com/p/40807662

0. 为什么要用Julia做优化？

本文是我在Julia中文社区2018用户见面会上关于用Julia进行优化建模及求解的分享内容。

本Tutorial主要介绍JuMP.jl,一种在Julia语言中的开源AML(Algebraic Modeling Language), 类似于AMPL, YALMIP, CVX, Poymo, GAMS等。JuMP的优化建模+solver内存传递速度，与其它商业/开源AML的比较见下表。不涉及Convex.jl，类似Matlab中的CVX，由Boyd et al. 开发的另一种Julia中的AML。

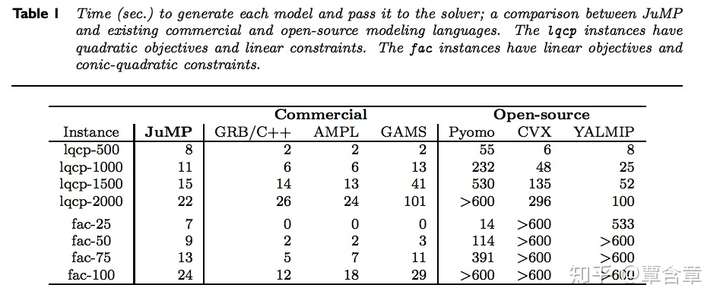
该表来自：Dunning, Iain, Joey Huchette, and Miles Lubin. JuMP: A modeling language for mathematical optimization. SIAM Review 59.2 (2017): 295-320. 更多JuMP的实现细节和与其它AML的比较可参

我们发现JuMP在优化建模速度上不输商业AML，比其它的开源AML要明显快出许多。

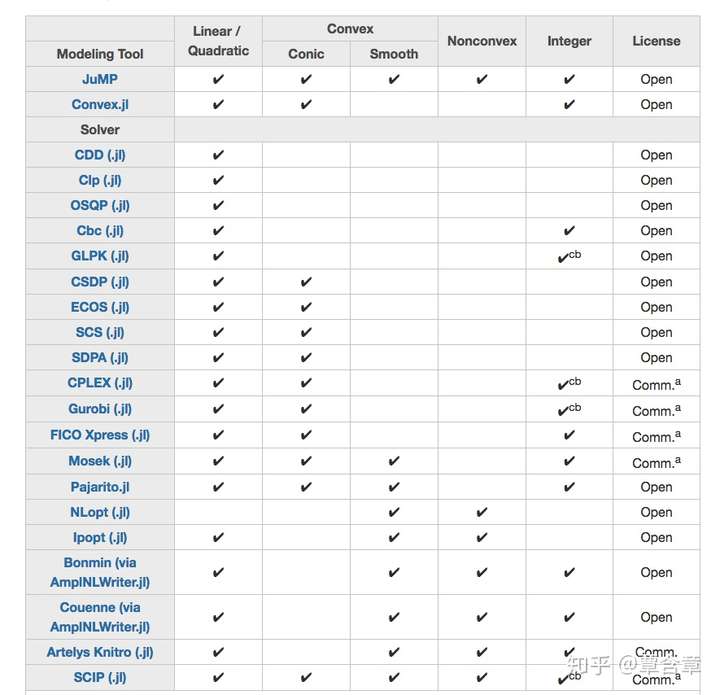
该表来自：https://www.juliaopt.org/

JuMP的另一大好处在于无缝衔接各种商业/开源solver: Gurobi, CPLEX, SCIP, Knitro, Mosek等......

1. 优化建模初步（最基本的线性规划）

(这部分主要针对优化理论零基础的读者，例子来自于——覃含章：运筹学中应该如何理解互补松弛性。这条性质又该如何运用?)

假设你是一个木匠，出售手工制作的木头桌子和木头椅子。现在你想要制定一个生产计划，让这个月的利润最大化。

注意，生产一张桌子，或者一把椅子，都需要消耗一定数量的木材和时间，而作为一个手工小作坊，你每个月能用来生产的时间是有限的，你每个月能进到的木材也是有限的。

简单起见，我们假定桌子的利润固定为一张10元，椅子为一把3元。生产一张桌子需要5单位木材和3单位时间，生产一把椅子需要2单位木材和1单位时间。且我们所有生产的桌子椅子都是能被卖掉的。先假设当月我们总共有200单位木材和90单位时间。

显然，这个生产规划问题可以用线性规划来建模：

$\begin{align*} \max~ & 10x_1+3x_2\tag{P}\\ \text{s.t. } & 5x_1+2x_2\leq 200 \tag{P1}\\ & 3x_1+x_2\leq 90 \tag{P2} \\ & x_1,x_2\geq 0. \end{align*}$

根据对偶理论，我们也知道等价的对偶问题为：

$\begin{align*} \min~ & 200p_1+90p_2 \tag{D}\\ \text{s.t. } & 5p_1+3p_2\geq 10\tag{D1}\\ & 2p_1+p_2\geq 3\tag{D2} \\ & p_1,p_2\geq 0. \end{align*}$

# 利用JuMP求解原问题
function CarpenterPrimal(c,A,b)# 定义Model对象, OutputFlag = 0指不输出logPrimal = Model(solver = GurobiSolver(OutputFlag = 0))# 定义变量，注意这里使用了宏（macro），宏的调用也是Julia&JuMP高效编译/元编程(metaprogramming)的重要技巧@variable(Primal, x[1:2]>=0)# 定义不等式约束constr = @constraint(Primal, A*x.<=b)# 定义目标函数@objective(Primal, Max, dot(c,x))# 求解solve(Primal)# 返回最优目标函数值，最优解（原问题），最优解（对偶问题）return getobjectivevalue(Primal), getvalue(x), getdual(constr)
end

调用CarpenterPrimal函数，得到最优解是生产30张桌子，不生产椅子： $x_1^*=30,x_2^*=0.$ 。接下来我们看一下这个解背后所蕴含的其他信息。同时，对应木材和时间的影子价格 $p_1^*,p_2^*$ 是0和10/3。

我们指出，也可以利用JuMP进行敏感度分析（Sensitivity Analysis）。考虑以下四个（P）的变种问题：（当然，其实都可以手解，用CarpenterPrimal进行验证）

(1) 把(P)中的(P1)右端项改成250，即木材总量增加。其余不变。最优解是什么？
(2) 把(P)中的(P2)右端项改成120，即生产时间增加。其余不变。最优解是什么？增加的利润（相比原来的(P)）和（P2）的影子价格的关系？
(3) 假设桌子的单位利润不变，椅子的单位利润增加到多少的时候(P)的最优解开始生产椅子（而不生产桌子）？
(4) 假设时间的总量仍为90，木材的总量减少到多少的时候木材的影子价格严格大于0（时间的影子价格反而变成0）？

如对这些基本概念不熟悉，可参阅本节一开始提到的我的回答。

2. 线性规划中的Column Generation实例：大规模additive convex regression

给定数据 $Y\in \mathbb{R}^n, X\in \mathbb{R}^{n\times d},$ 我们考虑以下线性规划问题：

$\begin{align*} \min~ & \sum_{i=1}^n \left|Y_i-\sum_{j=1}^d f_j(X_{ij})\right|\\ \text{s.t. } & f_j:\mathbb{R}\rightarrow\mathbb{R} \text{ is convex}, \forall~j=1,\ldots, d. \end{align*}$

注意我们如果在目标函数中再额外加上正则项 $\lambda\sum_{j=1}^d \left| \sum_{i=1}^n f_j(X_{ij}) \right|$ （ $\lambda>0$ ）, 则我们可以得到一个稀疏的(sparse) additive model。详见：Ravikumar, Pradeep, et al. "Sparse additive models." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71.5 (2009): 1009-1030.

上述模型是线性规划因为等价于(记 $[:]_j$ 为 $X_{:j}$ 升序排序后的对应原index的序列)

$\begin{align*} \min~ & \sum_{i=1}^n r_i^++r_i^-\\ \text{s.t. } & Y_i - \sum_{j=1}^d f_{ij} = r_i^+-r_i^-, \forall~i=1,\ldots,n\\ & (f_{[i]_j j}-f_{[i-1]_j j})(X_{[i+1]_j j}-X_{[i]_j j})\leq (f_{[i+1]_j j}-f_{[i]_j j})(X_{[i]_j j}-X_{[i-1]_j j}),\forall~i=2,\ldots,n-1,\forall~j=1,\ldots,d. \end{align*}$

# 生成样本
n = 5000
d = 2
function_list = [x->0.5*abs.(x).^2,x->2*abs.(x),x->5*x.^2,x->0.5*exp.(x),x->0.3*x,x->0.7*x,x->2*x.^2,x->0.1*exp.(x),x->x.^2,x->exp.(x)]
srand(123)
X = rand(n,d) - 0.5
Y = 0.02*randn(n,1)
for i = 1:dY = Y + function_list[mod(i-1,10)+1](X[:,i])
end

# Full-sized的线性规划模型
function Full_ConvReg(Max_T)M_conv_full = Model(solver=GurobiSolver(TimeLimit=Max_T, OutputFlag=0))@variable(M_conv_full, f_hat[1:n,1:d])@variable(M_conv_full, Res_pos[1:n]>=0)@variable(M_conv_full, Res_neg[1:n]>=0)    for k = 1:dxx = X[:,k] ids = sortperm(vec(xx),rev=false)xx = xx[ids]for i in 2:(n-1)d1 = (xx[i+1]-xx[i]); d2=(xx[i]-xx[i-1]);@constraint(M_conv_full, (f_hat[ids[i],k]-f_hat[ids[i-1],k])*d1<=(f_hat[ids[i+1],k]-f_hat[ids[i],k])*d2);end   endfor i in 1:n@constraint(M_conv_full, Y[i] - sum(f_hat[i,k] for k=1:d) == Res_pos[i] - Res_neg[i]  )end  @objective(M_conv_full, :Min, sum(Res_pos[i] + Res_neg[i] for i = 1:n) )   solve(M_conv_full)   return getvalue(f_hat)
end

接下来我们介绍什么是Column Generation，并展示如何对上述问题利用JuMP和Gurobi进行Column Generation。这种方法是基于单纯形法（simplex methopd）的。即我们在一开始默认所有的变量都为0且不是基变量，而在每步iteration的时候利用前一轮的对偶变量的值计算reduced cost(只需要计算一步矩阵和向量的乘法)，并将reduced cost最负的变量加入（成为基变量）。同时注意到，因为原问题的约束矩阵实际上具有分块特性（按照 $j=1,…,d$ 分块），实际上我们可以采取Dantzig-Wolfe的formulation，即利用一个cyclic的update方式，在每个iteration对每个block单独计算reduced cost（比一起算快了 $d$ 倍）。当所有reduced cost非负的时候，找到最优解：算法终止。

对Dantzig-Wolfe或者column generation不太了解的同学，请见一些经典的资料，如：https://perso.uclouvain.be/anthony.papavasiliou/public_html/DantzigWolfe.pdf

当然，第五个例子里的constraint generation其实原理和column(variable) generation类似，那个例子对于零背景知识的同学可能更容易看。

# Column Generation化的线性规划模型
function CG_ConvReg(Max_T)# build the LO: no Δ includedM_conv = Model(solver=GurobiSolver(TimeLimit = Max_T,OutputFlag = 0,Method = 0))@variable(M_conv, Res_pos[1:n]>=0)@variable(M_conv, Res_neg[1:n]>=0)@constraintref constr[1:n]MaxIter = 1000XX = zeros(n,d)L = zeros(n,n+2,d)ids = convert(Array{Int64,2},zeros(n,d))ids_rec = convert(Array{Int64,2},zeros(n,d))for k = 1:d# sort the sequencesids[:,k] = sortperm(vec(X[:,k]),rev=false)ids_rec[:,k] = sortperm(ids[:,k],rev=false)XX[:,k] = X[ids[:,k],k]  # needed for column generationL[:,1,k] = ones(n,1)L[:,2,k] = -ones(n,1)L[2,3,k] = XX[2] - XX[1]L[2,4,k] = - XX[2] + XX[1]for i = 3:nL[i,3,k] = XX[i,k] - XX[1,k]L[i,4,k] = - XX[i,k] + XX[1,k]L[i,5:i+2,k] = [XX[i,k]-XX[j+1,k] for j=1:i-2]'endL[:,:,k] = L[ids_rec[:,k],:,k] end@constraint(M_conv, constr[i=1:n], Res_pos[i] - Res_neg[i] == Y[i])@objective(M_conv, :Min, sum(Res_pos[i] + Res_neg[i] for i = 1:n) )solve(M_conv)dual_var = getdual(constr)NewColumns = [Variable[] for i=1:d]IdxList = [[] for i=1:d]                       # Implement column generation                 iter = 1   flag = vec(ones(d,1))while sum(flag) > 1e-3 && iter < MaxIter#for t = 1:30for k = 1:d    if flag[k] == 1 Δ_r = -L[:,:,k]'*dual_var elsecontinueendif findmin(Δ_r)[1] < -1e-3idx = findmin(Δ_r)[2]constr_list = constr[1:n]coeff_list = L[:,idx,k]@variable(M_conv, Δ_temp >= 0, objective = 0., inconstraints = constr_list, coefficients =  coeff_list ) #print("CG iteration ", iter,": enter Δ ",idx," for covariate ",k, "\n")push!(NewColumns[k],Δ_temp)push!(IdxList[k],idx)solve(M_conv) iter = iter + 1dual_var = getdual(constr);else#print("Skip covariate ", k,"\n")flag[k] = 0endendend#print("CG ends after ", iter-1, " itertaions.\n")# Retrieve the ϕ valuesdelta = zeros(n+2,d)zz = zeros(n,d)phi = zeros(n,d)for k = 1:ddelta[IdxList[k],k]=getvalue(NewColumns[k])if isempty(find(IdxList[k].==2))zz[1,k] = delta[1,k]elsezz[1,k] = -delta[2,k]endif isempty(find(IdxList[k].==4))zz[2,k] = delta[3,k]elsezz[2,k] = -delta[4,k]endphi[1,k] = zz[1,k]phi[2,k] = zz[1,k]+zz[2,k]*(XX[2,k]-XX[1,k])                           for i = 3:nzz[i,k] = zz[i-1,k] + delta[i+2,k]phi[i,k] = zz[i,k]*(XX[i,k]-XX[i-1,k])+phi[i-1,k]endendreturn phi
end

phi = CG_ConvReg(200);
# 画出第一维上的解
XX = zeros(n,d)
ids = convert(Array{Int64,2},zeros(n,d))
ids_rec = convert(Array{Int64,2},zeros(n,d))for k = 1:d # sort the sequencesids[:,k] = sortperm(vec(X[:,k]),rev=false)ids_rec[:,k] = sortperm(ids[:,k],rev=false)XX[:,k] = X[ids[:,k],k]
end
plot(XX[:,1],phi[:,1])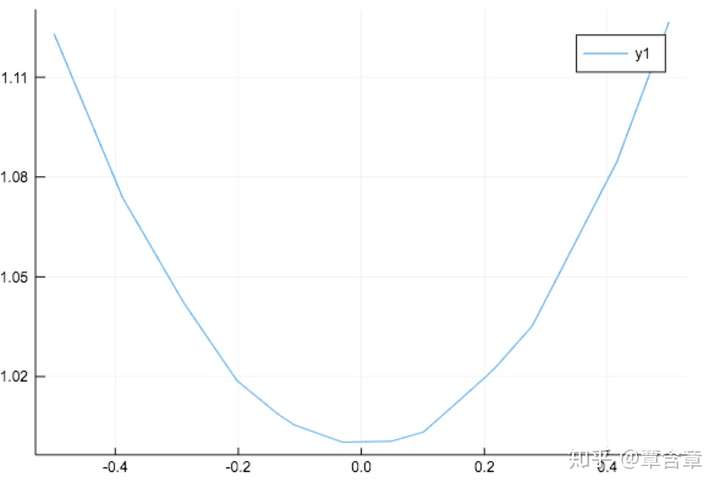

接下来我们比较这两种formulation的求解速度。

@benchmark CG_ConvReg(200)

@benchmark Full_ConvReg(600)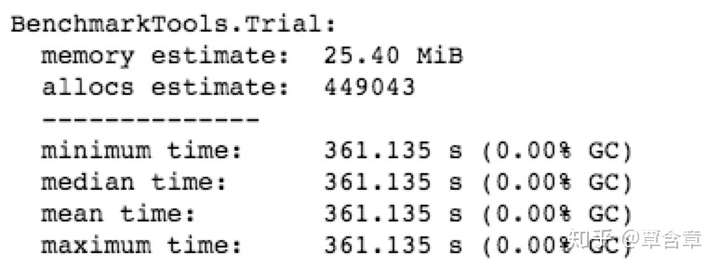

令人惊讶的是，基于古老的单纯形法和Column Generation的算法竟然要远快于Gurobi求解LP默认的non-deterministic concurrent方法！这证明针对特定的优化问题，有时候更聪明的建模会给你更快的算法。

3. 鲁棒线性规划（Robust Linear Programming）

我们考虑最小费用流问题（minimum cost flow），其中每条边上的cost具有不确定性（uncertainty）。即我们考虑一个有向图 $G=(V,E)，V={1,…,n}$ ,我们考虑优化问题：

$\begin{align*} \min~ & \sum_{(i,j)\in E} c_{ij}x_{ij}\\ \text{s.t. } & \sum_{(1,i)\in E}x_{1i} = 1\\ & \sum_{(i,n)\in E}x_{in} = 1\\ & \sum_{(i,j)\in E}x_{ij} = \sum_{(j,k)\in E} x_{jk},\forall~j\in V \backslash \{1,n\}\\ & 0\leq x_{ij}\leq C_{ij}. \end{align*}$

# Nominal Problem
function NominalProblem(n,μ,δ)NetworkModel = Model(solver=GurobiSolver(OutputFlag=0))capacity = (ones(n,n)-eye(n,n))*0.5capacity[1,n] = 0capacity[n,1] = 0@variable(NetworkModel, flow[i=1:n,j=1:n]>=0)@constraint(NetworkModel, flow .<= capacity)@constraint(NetworkModel, sum(flow[1,i] for i=1:n)==1)@constraint(NetworkModel, sum(flow[i,n] for i=1:n)==1)for j = 2:n-1@constraint(NetworkModel, sum(flow[i,j] for i=1:n) == sum(flow[j,k] for k=1:n)  )end@objective(NetworkModel,Min, sum(flow[i,j]*μ[i,j] for i=1:n for j=1:n) );solve(NetworkModel)return getvalue(flow)
end

我们考虑以下三种uncertainty set:

$\begin{align*} & (i)~\text{Box Uncertainty}: \mathcal{U}_{L_\infty} = \{\textbf{c}:μ_{ij}-\delta_{ij}\gamma_{ij}\leq c_{ij}\leq \mu_{ij}+\delta_{ij}\gamma_{ij}, \|\gamma\|_{\infty}\leq \Gamma \}\\ & (ii)~\text{Polyhedral Uncertainty}: \mathcal{U}_{L_1} = \{\textbf{c}:μ_{ij}-\delta_{ij}\gamma_{ij}\leq c_{ij}\leq \mu_{ij}+\delta_{ij}\gamma_{ij}, \|\gamma\|_1\leq \Gamma \}\\ & (iii)~\text{Elliopsoidal Uncertainty}: \mathcal{U}_{L_2} = \{\textbf{c}:μ_{ij}-\delta_{ij}\gamma_{ij}\leq c_{ij}\leq \mu_{ij}+\delta_{ij}\gamma_{ij}, \|\gamma\|_2\leq \Gamma \}\\ \end{align*}$

其实，容易知道(i)(ii)的robust min cost flow问题仍可写成一个线性规划，(iii)的robust min cost flow问题可写成一个二阶锥规划问题(second-order cone optimization)。不过我们这里展示利用JuMPeR包可以省去推导robust counterpart的步骤。

# Robust Problem
function RobustProblem(n,μ,δ,Γ,norm_type)NetworkModel_robust = RobustModel(solver=GurobiSolver(OutputFlag=0))capacity = (ones(n,n)-eye(n,n))*0.5capacity[1,n] = 0capacity[n,1] = 0@variable(NetworkModel_robust, flow[i=1:n,j=1:n]>=0)@uncertain(NetworkModel_robust, cost[i=1:n,j=1:n])@uncertain(NetworkModel_robust, r[i=1:n,j=1:n])@variable(NetworkModel_robust, obj) for i = 1:nfor j = 1:n@constraint(NetworkModel_robust, cost[i,j] == μ[i,j]+r[i,j]*δ[i,j])endend  @constraint(NetworkModel_robust, norm(r,norm_type) <= Γ)@constraint(NetworkModel_robust, flow .<= capacity)@constraint(NetworkModel_robust, sum(flow[1,i] for i=1:n) == 1)@constraint(NetworkModel_robust, sum(flow[i,n] for i=1:n) == 1)for j = 2:n-1@constraint(NetworkModel_robust, sum(flow[i,j] for i=1:n) == sum(flow[j,k] for k=1:n))end@constraint(NetworkModel_robust, sum(cost[i,j]*flow[i,j] for i=1:n for j=1:n) <= obj )@objective(NetworkModel_robust, Min, obj)solve(NetworkModel_robust)return getvalue(flow)
end

我们这里做一些仿真来看一下robust solution的表现。假设G是完全连同的，所有边的容量都是0.5，我们随机产生 $μ_{ij}∼Uniform(0,10)$ $δ_{ij}∼Uniform(0,μ_{ij})$ ，然后我们再随机产生 $c_{ij}$ 来看实际的cost的情况。我们以nominal problem的解为benchmark,输出robust solution的cost与其的差。

function Evaluation()n_type = [10,25,50,75,100]Γ_type = [1e-4,1e-1,1e1,1e4]report_data = zeros(13,5)for n_idx = 1:5n = n_type[n_idx]count = 2μ = 10*rand(n,n)δ = zeros(n,n)for i = 1:nfor j = 1:nδ[i,j] = μ[i,j]*rand()endendcost_sim = zeros(n,n)for i = 1:nfor j = 1:ncost_sim[i,j] = μ[i,j] + δ[i,j] * (rand()-0.5) * 2endendsol_0 = NominalProblem(n,μ,δ)report_data[1,n_idx] = sum(sum(cost_sim.*sol_0))for Γ in Γ_typeprint("n=",n," Γ=",Γ)sol_inf = RobustProblem(n,μ,δ,Γ,Inf)sol_1 = RobustProblem(n,μ,δ,Γ,1)sol_2 = RobustProblem(n,μ,δ,Γ,2)    report_data[count,n_idx] = sum(sum(cost_sim.*(sol_inf-sol_0)))report_data[count+1,n_idx] = sum(sum(cost_sim.*(sol_1-sol_0) ))report_data[count+2,n_idx] = sum(sum(cost_sim.*(sol_2-sol_0) ))count = count + 3endendreturn report_data
end
output = Evaluation();
# 输出Γ=10时三种uncertainty set给出的difference
temp_p = plot([10,25,50,75,100],output[8,:],xlabel = "n", label = "Uinf")
plot!(temp_p,[10,25,50,75,100],output[9,:], label = "U1")
plot!(temp_p,[10,25,50,75,100],output[10,:], label = "U2")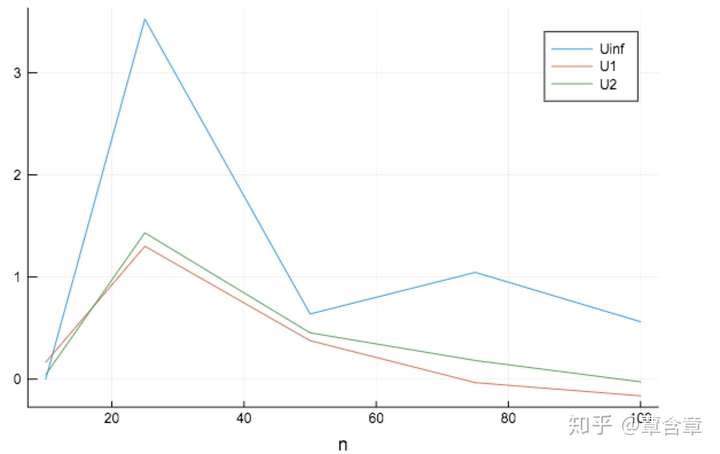

那么我们确实看到box constraint给出了更robust的solution，而L1/2 uncertainty构建下的鲁棒优化问题更mild一些。

JuMPeR也可以model多阶段的鲁棒优化问题，尤其比如是affinely-adjustable policy的(这比uncertainty set的formulation要松的多)。这里只是提一下，不详细介绍了，有兴趣的同学可以自行研究，其实也是很有用的。

4. 近似解Stable Number: 半正定规划/整数规划

一个无向图 $G=(V,E)$ 的stable(independent) set是V的一个子集，其中所有节点互相都不相连。 stable set的最大cardinality定义为α(G)，也叫做图的stability number. 假设|V|=n. 自然，其0/1整数规划可以写成：

$\begin{align} \alpha(G) = & \max_x~ \sum_{i=1}^n x_i\\ &\text{s.t. } x_i+x_j\leq 1,~ \text{if } (i,j)\in E,\\ & x_i\in \{0,1\},\forall~i=1,\ldots,n. \end{align}$

利用 $x_i+x_j≤1$ 和 $x_ix_j=0$ 等价，我们可以得到一个半正定规划的relaxation：

$\begin{align} \alpha(G) = & \max_X~ \text{tr}(ee^TX) \\ &\text{s.t. } X_{ij} = 0,~ \text{if } (i,j)\in E,\\ & \text{tr}(X) = 1,\\ & X\succeq 0,\\ & X\geq 0. \end{align}$

例子来源：Pena, Javier, Juan Vera, and Luis F. Zuluaga. "Computing the stability number of a graph via linear and semidefinite programming." SIAM Journal on Optimization 18.1 (2007): 87-105.

function StableBin(A)n = size(A,1)StableB = Model(solver = GurobiSolver(OutputFlag = 0))@variable(StableB, x[1:n], Bin)for i = 1:nfor j in find(A[i,:].== 1)@constraint(StableB, x[i] + x[j] <= 1)endend@objective(StableB, Max, sum(x))solve(StableB)return getobjectivevalue(StableB)
end

function StableSDP(A)n = size(A,1)StableDD = Model(solver = MosekSolver(MSK_IPAR_LOG = 0))@variable(StableDD, X[1:n,1:n])@SDconstraint(StableDD, X>=0)@constraint(StableDD, X.>=0)@constraint(StableDD, sum(sum(A.*X)) == 0 )@constraint(StableDD, sum(X[i,i] for i=1:n) == 1)@objective(StableDD, Max, sum(sum(X)))solve(StableDD)return getobjectivevalue(StableDD)
end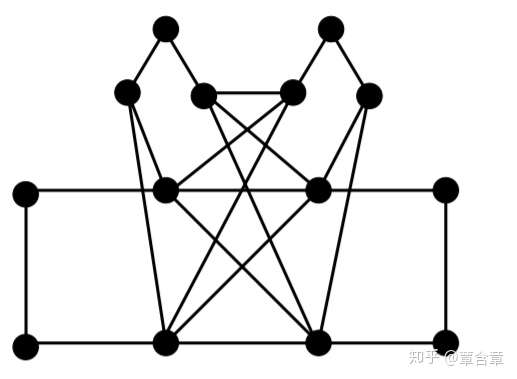

以这个G为例子。

A14 = [0 1 1 0 0 0 0 0 0 0 0 0 0 0; 1 0 0 1 0 0 0 0 0 0 0 0 0 0;1 0 0 0 1 1 0 0 1 0 0 1 0 0;0 1 0 0 1 1 0 0 1 0 0 1 0 0;0 0 1 1 0 0 1 0 0 0 1 0 0 1;0 0 1 1 0 0 0 1 0 0 1 0 0 1;0 0 0 0 0 1 0 1 0 0 0 0 0 0;0 0 0 0 0 1 1 0 0 0 0 0 0 0;0 0 1 1 0 0 0 0 0 1 0 0 0 0;0 0 0 0 0 0 0 0 1 0 1 0 0 0;0 0 0 0 1 1 0 0 0 1 0 1 0 0;0 0 1 1 0 0 0 0 0 0 1 0 1 0;0 0 0 0 0 0 0 0 0 0 0 1 0 1;0 0 0 0 1 1 0 0 0 0 0 0 1 0];
# α(G14) = 5
StableBin(A14)
# 松弛之后的解：5.694362954824882
StableSDP(A14)

5. Lazy Constriant Generation: 在整数规划中用分段线性函数近似L2球

我们指出Gurobi还暂不支持整数规划和column generation结合（即branch and price）,然而自定义user cut确是支持的（即branch and cut）！简单来说，即我们可以一开始只加入少量的约束，在一边求解整数规划的过程中将被violate的约束加入，因此也叫lazy callback。

这个例子来自于：https://github.com/JuliaOpt/juliaopt-notebooks/blob/master/notebooks/JuMP-LazyL2Ball.ipynb

我们要求解的问题是一个整数约束的二阶锥规划问题：

$\begin{align*} \max ~ & c^T x\\ \text{s.t. } & \|x\|_2\leq \Gamma,\\ & x\in \mathbb{Z}^n. \end{align*}$

function solve_ball(c, Γ, ϵ=1e-6)n = length(c)m = Model(solver=GurobiSolver(OutputFlag=0))# 初始consrtaint: 一个box@variable(m, -Γ ≤ x[1:n] ≤ Γ, Int)# 定义目标函数@objective(m, Max, dot(c,x))#核心：定义callback function，记录加入cut的数量num_callbacks = 0function norm_callback(cb)num_callbacks += 1N = getvalue(x)# 求得当前x的L2 normL = norm(N)# 如果足够小，说明已经得到一个可行解，即解最优if L ≤ Γ + ϵreturnend# 不然的话，加入cut!注意这个cut将使得x变得不可行（infeasible），下步迭代必然会得到一个新的解@lazyconstraint(cb, dot(N,x) ≤ Γ*L)end# 将callback函数加入JuMP/Gurobi模型addlazycallback(m, norm_callback)#求解solve(m)return getvalue(x), num_callbacks
end#产生一个随机样例
srand(1234)
n = 2
c = rand(n)
Γ = 50.0# 求解，输出callback次数
sol, num_callbacks = solve_ball(c, Γ)
println(sol)
println(norm(sol))
println(num_callbacks)

经过11次lazycallback我们得到最优解。接下来还有个交互的例子，我这边懒得做动画了，只给code。效果请自行在jupyter notebook里体验。实际上就是说可以手动在bar上调整参数看到不同情况下的最优解和可行域在二维平面的图像。

# 这里展示Interact和Compose包，可用来进行交互
# 画出2D情况下的解
set_default_graphic_size(8cm, 8cm)@manipulate for c1 in -1:0.1:+1, c2 in -1:0.1:+1, logϵ in -4:2sol, _ = solve_ball([c1,c2], 100, 10.0^logϵ)compose(context(),compose(context(),line([(0.5,0.5),(0.5+sol[1]/300,0.5+sol[2]/300)]),Compose.stroke("black")),compose(context(),circle((0.5 + (100/norm(sol))*sol/300)...,0.02),fill("red")),compose(context(),circle(0.5,0.5,0.333),fill("lightblue")))
end

6. 一般的非线性整数规划：密堆积球问题

我们考虑这样一个问题：有k个半径为r的球和一个尺寸d1×d2的长方形盒子，是否有办法将这些球塞入长方形？显然，一个更一般的问题是对任意长方形找到最大的k。不过这个一般的问题可以通过顺序求解（不断增大k）之前的决策问题来解决，所以我们就讨论给定k的决策问题。

定义变量 $(p_{11},…,p_{1k}),(p_{21},…,p_{2k} )$ 为圆心的x和y坐标. 那么决策问题可以用如下非凸非线性规划问题来求解, 也见：Birgin, Ernesto G., J. M. Martınez, and Débora P. Ronconi. "Optimizing the packing of cylinders into a rectangular container: a nonlinear approach." European Journal of Operational Research 160.1 (2005): 19-33.

$\begin{align} \min~ & \sum_{i\neq j\in \{1,\ldots, k\} } \max\left(0,2r - \sqrt{(p_i^1-p_j^1)^2+(p_i^2-p_j^2)^2} \right)\\ \text{s.t. } & r\leq p_1^i\leq d_1-r,\forall~ i=1,\ldots,k, \\ & r\leq p_2^i\leq d_2-r,\forall~ i=1,\ldots,k. \\ \end{align}$

和上一节思路类似，我们这里也利用分段线性函数和整数规划来近似这里的L2函数。当然，我们这里采取更一般的做法，利用PiecewiseLinear包来方便完成。具体来说，我们考虑用整数线性规划近似如下非线性规划中的非凸约束。

$\begin{align} \min~ & \sum_{i\neq j\in \{1,\ldots, k\} } z_{ij}\\ \text{s.t. } & z_{ij}\geq 2r - \sqrt{(p_i^1-p_j^1)^2+(p_i^2-p_j^2)^2}, \forall ~ i\neq j\in \{1,\ldots,k\},\\ &r\leq p_1^i\leq d_1-r,\forall~ i=1,\ldots,k, \\ & r\leq p_2^i\leq d_2-r,\forall~ i=1,\ldots,k. \\ & z_{ij}\geq 0, \forall ~ i\neq j\in \{1,\ldots,k\}. \end{align}$

# 画图
function PlotCirclesRectangle(p1,p2)p = scatter((p2),(p1))for i = 1:kplot!(p,(p2[i]).+r*cos.(linspace(0,2*π,100)), (p1[i]).+r*sin.(linspace(0,2*π,100)), color = "blue", legend=false, aspect_ratio = 1 )endplot!(p,linspace(0,d2,100),zeros(100,1),color = "red")plot!(p,zeros(100,1),linspace(0,d1,100),color = "red")plot!(p,linspace(0,d2,100),ones(100,1)*d1,color = "red")plot!(p,d2*ones(100,1),linspace(0,d1,100),color = "red")p
end

# 考虑这样一组问题
r = 25
d1 = 160
d2 = 190
k = 11;
# MIO
function PackCirclesGen(r,d1,d2,k,Method,MaxTime)tic()PackCircles = Model(solver = GurobiSolver(MIPGap = 1e-3, OutputFlag = 0, TimeLimit = MaxTime))@variable(PackCircles, p1[1:k]>=r)@variable(PackCircles, p2[1:k]>=r)@variable(PackCircles, s1[1:k,1:k])@variable(PackCircles, s2[1:k,1:k]>=0)@variable(PackCircles, z[1:k,1:k]>=0)@constraint(PackCircles, p1.<=d1-r)@constraint(PackCircles, p2.<=d2-r)for i = 1:kfor j = i+1:kif j - i > 2 continueend@constraint(PackCircles,s1[i,j] == p1[j]-p1[i])@constraint(PackCircles,s2[i,j] == p2[j]-p2[i])#使用PiecewiseLinearOpt包近似nonconvex constraintfun_dist = piecewiselinear(PackCircles, s1[i,j] , s2[i,j], -(j-i)*r*2:r/5:(j-i)*r*2, 0:r/5:(j-i)*r*2, (u,v) -> (u^2+v^2)^0.5, method=Method)@constraint(PackCircles, z[i,j] >=  2*r - fun_dist )endend@objective(PackCircles, Min, sum(z[i,j] for i = 1:k for j = i+1:k))solve(PackCircles)return getvalue(p1),getvalue(p2),toc()
end
p1,p2,time = PackCirclesGen(r,d1,d2,k,:ZigZagInteger,Inf);
# 一个可行解
PlotCirclesRectangle(p1,p2)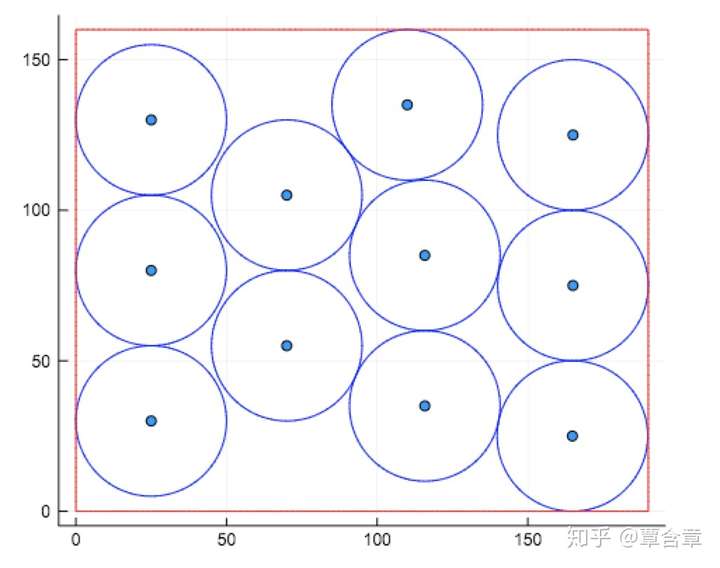

这个程序也可以作为这个知乎问题的探索：

2×1000的矩形中能放多少个直径为1的圆？www.zhihu.com

# 不同bivariate分段线性方法的比较
r = 21
d1 = 120
d2 = 120
k = 6;
Method_List = [:CC,:MC,:DisaggLogarithmic,:SOS2,:Logarithmic,:ZigZag,:ZigZagInteger]
# The experiment, note the cutoff time set as 600 seconds
for Method in Method_Listp1,p2,time = PackCirclesGen(r,d1,d2,k,Method,600)print("The method ", Method, " uses ", time, " seconds!\n")
end

我们注意到不同的线性分段逼近方法的计算速度是大不一样的，ZigZag的速度最快，CC/MC这样的formulation一般不建议用。详细的理论方法请见：Huchette, Joey, and Juan Pablo Vielma. "Nonconvex piecewise linear functions: Advanced formulations and simple modeling tools."

7. 更多

这篇Tutorial的GitHub链接，包括meetup上其它的julia相关资料：

JuliaCN/MeetUpMaterialsgithub.com

其它JuMP支持的优化拓展包可见：https://www.juliaopt.org/packages/

比如，支持多目标优化的MultiJuMP.jl，机会约束（chance constraint）的JuMPChance.jl，多项式（polynomial）优化的 PolyJuMP.jl，还有支持随机动态规划，非线性控制，平衡约束问题，图论算法，元启发式算法等等的package。