计算几何基本知识整理

向量

向量有方向与长度

两个点可以得到一个向量,如果交换点对位置，向量的方向也会取反。

要注意的是，向量本身只有方向和长度。

方便起见，我们可以简单地用二元组\((x,y)\)表示一个向量，即默认起点为原点\((0,0)\)。

前置知识：极角

\(update\ on\ 7.13.2019\)

定义

在极坐标系中，平面上任何一点到极点的连线和极轴的夹角叫做极角

向量的极角可以理解为其平移至原点时与x轴的夹角。

计算方法

对于向量\((x,y)\),其极角

\(\theta=tan^{-1}(\large\frac{y}{x})\)

\(Code:\)

double theta=atan2(y,x);//没传错，atan2函数就是这样

向量的运算

• 向量与一般数的运算，几何意义上，向量乘以某个数x等价于将向量放大\(x\)倍。

  一般的，向量\((x,y)*k = (kx,ky)\)

• 向量的特殊运算。

  加减就直接对应分量相加减就好了，几何意义如下图。

  

  乘法,向量的乘法分为两种，点乘与叉乘。

  点乘

  也叫内积，数量积，几何意义由余弦定理得来，在上图的三角形ADB中，运用余弦定理就可以了

  定义:\(a*b=|a||b|cos\theta\)

  其中\(\theta\)表示向量\(a\)旋转到向量\(b\)经过的夹角。

  当用二元组表示时,形式如下，

  \((x_1,y_1)*(x_2,y_2) = x_1y_1+x_2y_2\)

  点积的几何意义为\(a\)在\(b\)上的模长乘上\(b\)的长度，过\(a\)端点向\(b\)做垂线即可看出。

  叉乘

  也叫外积，向量积

  定义:\(a\times b=|a||b|sin{\theta}\)

  当用二元组表示时，形式如下，

  \((x_1,y_1)\times(x_2,y_2)=x_1y_2-x_2y_1\)

  叉积的数量上的意义为对应平行四边形的面积，几何上好像对应一个更高维的向量，这个暂时用不到。

  若\(a \times b >0\) 则\(a\)在\(b\)的逆时针方向，即\(a\)的极角大于\(b\)，反之同理。

  注意\(a\times b =0\)时\(a\)与\(b\)重合，但可能反向。

  旋转

  将向量\(\overrightarrow{a}=(x,y)\)旋转角度\(\theta\)的公式为

  \((x_1,y_1) \rightarrow (x_1cos\theta-y_1sin\theta,x_1sin\theta+y_1cos\theta)\)

  我们设\(\overrightarrow{a}\)的极角为\(\beta\)

  向量\(\overrightarrow{a}=(|a|cos\beta,|a|sin\beta)\)

  旋转后得到的新向量\(\overrightarrow{a'}=(|a|cos(\beta+\theta),|a|sin(\beta+\theta))\)

  运用和角公式

  \(sin(\alpha+\beta)=sin\alpha cos\beta+cos\alpha sin\beta\)

  \(cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta\)

  展开化简即得。

其他技巧

\(1.\)求夹角

\(\theta=\large cos^{-1}(\large\frac{a*b}{|a||b|})\)

\(2.\)判断两个向量的相对位置

判断\(a\times b\)的正负即可

\(3.\)求一个向量在另一个向量上的投影(点到直线的投影同理)

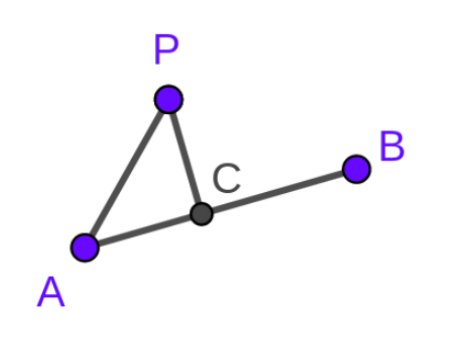
首先可以求出向量
\(AP*AB = |AC||AB|\)

\(AB*AB = |AB||AB|\)

\(\large \therefore \frac{|AP|}{|AB|}=\frac{AP*AB}{AB*AB}\)

\(\large\therefore \overrightarrow{AC}=\overrightarrow{AB}\times \frac{|AP|}{|AB|}\)

\(\therefore \large C=A+\overrightarrow{AB}\times \frac{|AP|}{|AB|}\)

\(4.\)点到直线距离

直线用一个点与从这个点出发的向量表示。

\(a\)为直线向量，b为向量端点与点的向量

原理:\(h=\large \frac{S}{a}\) 用平行四边形的面积除底即可

\(Length=\large\frac{a\times b}{|a|}\)

\(5.\)点到线段距离

同\(4\)，多判断特殊情况即可

这个给一下代码

inline int dcmp(double val){if(fabs(val) < eps)return 0;else return val > 0 ? 1 : -1;
}
double DisTS(Point P,Point A,Point B){ //Distance_to_Segmentif(A==B)return Length(P-A);Vector V1=B-A,V2=P-A,V3=P-B;if(dcmp(Dot(V1,V2))<0) return Length(V2);else if(dcmp(Dot(V1,V3))>0) return Length(V3);else return fabs(Cross(V1,V2)/Length(V1));
}

\(6.\)两直线的交点与相交判定

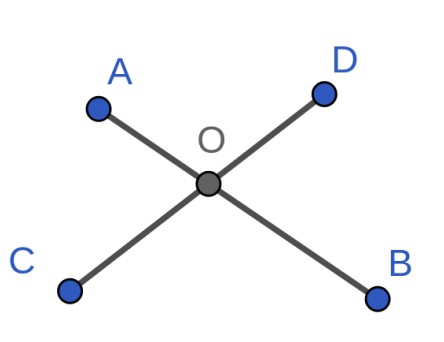
求交点常用的方法同样是利用叉积。

我们可以先求出 \(\triangle {ABC}\)和
\(\triangle {ABD}\) 的面积，从而得到\(OC\)与\(OD\)的比值。然后就可以得到\(O\)点坐标了

对于相交判定，先考虑直线与线段的相交判定，利用叉积判断线段两
点是否在直线的同侧即可。

//下面的两个判断函数均允许线段在端点处相交
bool IsLSI(Point A,Vector P,Point B,Vector Q){ //Is_Line_and_Segment_Has_IntersectionVector V1=B-A,V2=B+Q-A;return dcmp(Cross(P,V1))!=dcmp(Cross(P,V2));
}
bool IsSSI(Point A,Vector P,Point B,Vector Q){ //Is_Segment_and_another_Segment_Has_Intersectionreturn IsLSI(A,P,B,Q) && IsLSI(B,Q,A,P);
}

\(7.\)判断点在不规则多边形内

假想有一条从该点出发，水平向右的射线。依次枚举多边形相邻两
点，统计这两个点的连边穿过这条射线的次数。

如果次数为偶数，则点在多边形外部，否则在多边形内部。

原理大概是，直线穿越多边形边界时，只可能进入多边形或穿出多边形，这只能交替进行，而最后一次一定是穿出。

注意判断点在多边形上的情况，代码口胡，不保证正确。

bool IsPoS(Point P,Point A,Point B){ //Is_Point_on_Segmentif(A.x>B.x)swap(A,B);if(P.x<A.x || P.x>B.x || dcmp(Cross(B-A,P-A))return 0;return 1;
}
int IsPiP(Point P,Point Poly[],int n){ //Is_Point_in_Polygonint wn=0;For(i,1,n){Point A=Poly[i],B=Poly[i%n+1];//取两个点if(IsPoS(P,A,B))return -1;//判断是否在线段上if((A.x>P.x||B.x>P.x)&&dcmp(A.y-P.y)!=dcmp(B.y-P.y))wn^=1;//两个端点有一个在其右，并上下分布就一定穿过。}return wn;
}

凸包

定义

给出平面上的n个点，凸包为最小的能将其全部包含在内的凸几何图形。

一个形象的比喻就是橡皮筋箍图钉，要求包住全部图钉。

显而易见，凸包的顶点一定在原点集中。

计算方法

Graham 扫描法

先求上凸壳，将点按横坐标排序，依次加入一个斜率递减的单调栈中即可，

假设最后加入的点为A,B

如果当前加入的点C与A形成的向量在AB的左侧，ABC为凹的，B已经失去作用，可以从单调栈中弹出。

不断弹出直到满足凸多边形的性质即可。

具体判断斜率时，我们可以使用叉积的性质来判断，这样就可以有效的避免一些边界判断。

下凸壳同理。

执行部分\(O(n)\),排序\(O(nlog_2n)\)

总时间复杂度\(O(nlog_2n)\)

代码很短

洛谷凸包模板P2742的AC代码\((C++11)\)

/*
@Date    : 2019-07-12 18:11:10
@Author  : Adscn (1349957827@qq.com)
@Link    : https://www.cnblogs.com/LLCSBlog
*/
#include<bits/stdc++.h>
using namespace std;
#define IL inline
#define RG register
#define gi getint()
#define gc getchar()
#define File(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout)
IL int getint()
{RG int xi=0;RG char ch=gc;bool f=0;while(ch<'0'||ch>'9')ch=='-'?f=1:f,ch=gc;while(ch>='0'&&ch<='9')xi=(xi<<1)+(xi<<3)+ch-48,ch=gc;return f?-xi:xi;
}
IL void pi(int k,char ch=0)
{if(k<0)k=-k,putchar('-');if(k>=10)pi(k/10,0);putchar(k%10+'0');if(ch)putchar(ch);
}
const int N=1e4+10;
struct Vector{double x,y;};
struct Point{double x,y;explicit Point(double _x,double _y):x(_x),y(_y){}Point(){}
}p[N];
istream& operator >> (istream &is,Point &x){scanf("%lf%lf",&x.x,&x.y);return is;
}
Vector operator - (const Point &a,const Point &b){return (Vector){a.x-b.x,a.y-b.y};}//两点相减得到一个向量
double Length(Vector x){return sqrt(x.x*x.x+x.y*x.y);}//返回长度
double Cross(Vector x,Vector y){return x.x*y.y-x.y*y.x;}//叉乘
const double eps=1e-8;
int judge(double k){if(fabs(k)<eps)return 0;return k>0?1:-1;}//防止精度问题，判断浮点数正负
Point stk[N];
int top,n;
int main(void)
{n=gi;for(int i=1;i<=n;++i)cin>>p[i];sort(p+1,p+n+1,[&](Point a,Point b){return a.x==b.x?a.y<b.y:a.x<b.x;});for(int i=1;i<=n;++i){while(top>1&&judge(Cross(stk[top]-stk[top-1],p[i]-stk[top-1]))<0)--top;stk[++top]=p[i];}int tmp=top;for(int i=n-1;i>1;--i){while(top>tmp&&judge(Cross(stk[top]-stk[top-1],p[i]-stk[top-1]))<0)--top;stk[++top]=p[i];}stk[0]=stk[top];double ans=0;for(int i=1;i<=top;++i)ans+=Length(stk[i]-stk[i-1]);printf("%.2lf",ans);return 0;
}

\(Problem\ List:\)

练手毒瘤卡精度题，\(SHOI2012\) 信用卡凸包

求凸包面积

\(update\ on\ 7.14.2019\)

这个比较简单，

我们把一个n个点的凸包拆成n-2个三角形来处理，用向量叉乘算三角形面积

具体来说就是取0号点A为定点，依次枚举相邻端点B,C。

答案累加上\(\frac12{|AB|\times |AC|}\)

代码略。

动态凸包

平衡树维护动态凸包

支持以下操作

• 查询面积 \(O(1)\)
• 动态插入 均摊\(O(log_2n)\)
• 查询某点是否在凸包内 \(O(log_2n)\)

在上下凸壳各维护一个以横坐标为关键字的平衡树。

在平衡树上找到对应点的位置，用叉积判断新加入的点是否在凸包内。

向左右依次删点，顺便维护凸包面积就可以了。

模板题:\(Codeforce\ 70D\)

太毒瘤，不想写，有空再更新吧。

半平面交

\(update\ on\ 7.13.2019\)

定义

半平面就是对于一条给定直线，半平面就是其左（右）侧的平面。

顾名思义，半平面交就是半平面的交集。

计算方法

类似于凸包的做法，和凸包又有所不同。

按照之前所说的，直线可以表示一个半平面，

先将所有半平面按照对应直线极角来排序，按照顺序加入一个双端队列。

每次新加入一个半平面，就判断一下队首两个半平面的交点，队尾两个半平面的交点，与新的半平面的位置关系，
前后弹队列。

最后注意两个边界：

• 当两个半平面的极角相同的时候，需要取更靠左的那一个。
• 最后收尾的时候，可能第一个半平面还有可能把最后的半平面排
  除掉，因此最后还要弹一次队列。

Point LI(Point A,Vector P,Point B,Vector Q){ //Line_IntersectionVector V=A-B;return A+P*Cross(Q,V)/Cross(P,Q);
}
struct Line{Point P;Vector V;double ang;Line(Point a=Point(0,0),Vector b=Vector(0,0)):P(a),V(b){ang=atan2(V.y,V.x);}//极角bool operator < (const Line &rhs) const {return ang<rhs.ang;}
};
bool OnLeft(Line L,Point P){return Cross(L.V,P-L.P)>0;}//点在直线左侧
int HpI(Line L[],int n,Point Poly[]){sort(L+1,L+n+1);int f,l;static Point p[N];static Line q[N];q[f=l=1]=L[1];For(i,2,n){while(f<l && !OnLeft(L[i],p[l-1]))l--;//如果原来的交点在新加入直线的右边，就没用了。while(f<l && !OnLeft(L[i],p[f]))f++;q[++l]=L[i];if(!dcmp(Cross(q[l].V,q[l-1].V))){//与上一条直线极角相同l--;if(OnLeft(q[l],L[i].P))q[l]=L[i];}if(f<l)p[l-1]=LI(q[l].P,q[l].V,q[l-1].P,q[l-1].V);//新的交点}while(f<l && !OnLeft(q[f],p[l-1]))l--;if(l-f<=1)return 0;p[l]=LI(q[l].P,q[l].V,q[f].P,q[f].V);int cnt=0;for(int i=f;i<=l;i++)Poly[++cnt]=p[i];return cnt;
}

\(Problem\ List:\)

$UVA 1475  Jungle  Outpost $

$Solution $

\(update \ on \ 7.14.2019\)

计算几何板子+二分答案即可，思维难度不高

/*
@Date    : 2019-07-13 22:00:02
@Author  : Adscn (1349957827@qq.com)
@Link    : https://www.cnblogs.com/LLCSBlog
*/
#include<bits/stdc++.h>
using namespace std;
#define IL inline
#define RG register
#define gi getint()
#define gc getchar()
#define File(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout)
IL int getint()
{RG int xi=0;RG char ch=gc;bool f=0;while(ch<'0'||ch>'9')ch=='-'?f=1:f,ch=gc;while(ch>='0'&&ch<='9')xi=(xi<<1)+(xi<<3)+ch-48,ch=gc;return f?-xi:xi;
}
IL void pi(int k,char ch=0)
{if(k<0)k=-k,putchar('-');if(k>=10)pi(k/10,0);putchar(k%10+'0');if(ch)putchar(ch);
}
const int N=5e4+7;
const double eps=1e-9;
int dcmp(double x)
{if(fabs(x)<eps)return 0;return x<0?-1:1;
}
struct Point{double x,y;Point(double a,double b):x(a),y(b){}Point(){}
}po[N];
typedef Point Vector;
Point operator + (const Point & a, const Point & b){return (Point){a.x+b.x,a.y+b.y};}
Point operator - (const Point & a, const Point & b){return (Point){a.x-b.x,a.y-b.y};}
Point operator * (const Point &a, const double &b){return (Point){a.x*b,a.y*b};}
bool operator < (const Point & a, const Point & b){return (!dcmp(a.x-b.x))?(dcmp(a.y-b.y)<0):(dcmp(a.x-b.x)<0);
}
//bool operator == (const Point &a, const Point &b){return !(dcmp(a.x-b.x)&&dcmp(a.y-b.y));}
double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
struct Line{Point st;Vector v;double ang;Line(Point a,Vector ve):st(a),v(ve){ang=atan2(v.y,v.x);}Line(){}
};
bool operator < (const Line &a,const Line &b){return a.ang<b.ang;}
inline Point LI(Line a,Line b)
{Vector V=a.st-b.st;return a.st+a.v*(Cross(b.v,V)/Cross(a.v,b.v));
}
inline bool OnLeft(Line a,Point b){return Cross(b-a.st,a.v)<0;}
int HpI(Line L[],int n)
{sort(L+1,L+n+1);static Point p[N];static Line q[N];int head,tail;q[head=tail]=L[1];for(int i=2;i<=n;++i){while(head<tail&&!OnLeft(L[i],p[tail-1]))--tail;//此时交点比边少while(head<tail&&!OnLeft(L[i],p[head]))++head;q[++tail]=L[i];if(!dcmp(Cross(q[tail].v,q[tail-1].v))){--tail;if(OnLeft(q[tail],L[i].st))q[tail]=L[i];}if(head<tail)p[tail-1]=LI(q[tail-1],q[tail]);}while(head<tail&&!OnLeft(q[head],p[tail-1]))--tail;if(tail-head<=1)return 0;p[tail]=LI(q[head],q[tail]);return 1;
}
int n;
inline bool check(int mid)
{static Line Li[N];for(int i=1;i<=n;++i)Li[i]=(Line){po[i],po[i]-po[(i+mid)%n+1]};return HpI(Li,n);
}
int main(void)
{#ifndef ONLINE_JUDGEFile("file");#endifwhile(cin>>n){for(int i=1;i<=n;++i)po[i]=(Point){static_cast<double>(gi),static_cast<double>(gi)};int le=1,ri=n,ans;while(le<=ri){int mid=(le+ri)>>1;if(check(mid))le=mid+1;else ans=mid,ri=mid-1;}pi(ans,'\n');}return 0;
}

旋转卡壳

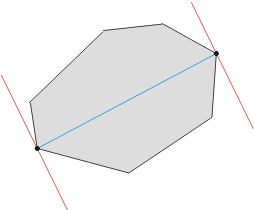
先放一张图，

定义

旋转卡壳，就是弄两条平行的直线卡在凸包的两边，绕着凸包旋转一周，对于每一对直线上对应出现过的点对的距离长度取最大值来求凸包的直径。

其中出现的点对被称为对踵点。

计算方法

如果真的这样写的话会写死的。。。

我们发现对于凸包上的一个定点，顺时针方向的凸包上的其他的点到此点的距离是先单调上升，再单调下降的。

于是我们只要考虑两个指针指向对踵点A,B,

先指定A=1,B=2，向顺时针方向不断移动B点，一旦A到B的距离不再单调上升，就存下最大距离，并移动A点。

显然时间复杂度为\(O(n)\)

不过肯定要先做一遍凸包。

所以复杂度为\(O(nlog_2n)\)

我们判断A与B的距离是否上升，等价于判断矢量|B B+1|的方向在矢量|A A+1|顺时针处，用叉乘就可以了。

如果搞不清楚用勾股定理应该也可以

\(Code:\)

const int N=1e5+10;
Point P[N<<2],Poly[N<<2];
inline int ConvexHull(Point A[],int n,Point Ans[]){sort(A+1,A+n+1);int cnt=0;For(i,1,n){while(cnt>1 && Cross(Ans[cnt]-Ans[cnt-1],A[i]-Ans[cnt-1])<=0)cnt--;Ans[++cnt]=A[i];}int k=cnt;Fordown(i,n-1,1){while(cnt>k && Cross(Ans[cnt]-Ans[cnt-1],A[i]-Ans[cnt-1])<=0)cnt--;Ans[++cnt]=A[i];}return cnt-1;
}
inline double Rotating_Calipers(Point A[],int n){n=ConvexHull(A,n,Poly);Poly[n+1]=Poly[1];double ans=0;for(int u=1,v=2;u<=n;u++){while(true){int val=dcmp(Cross(Poly[u+1]-Poly[u],Poly[v+1]-Poly[v]));if(val<=0){ans=max(ans,Length(Poly[u]-Poly[v]));if(!val)ans=max(ans,Length(Poly[u]-Poly[v+1]));break;}v=v%n+1;}}return ans;
}

\(Problem\ List\)

\(BZOJ1069\ [SCOI2007]\)最大土地面积

\(Solution\)

首先不难证明四个点一定都在凸包上。

考虑枚举四边形的对角线，这样我们只要最大化对角线两边的三角形面积即可。这个只需要在枚举
第二个点的过程中，顺便做旋转卡壳求出两边距离最远的点即可。

时间复杂度\(O(n^2)\)

/*
@Date    : 2019-07-14 21:50:18
@Author  : Adscn (1349957827@qq.com)
@Link    : https://www.cnblogs.com/LLCSBlog
*/
#include<bits/stdc++.h>
using namespace std;
#define IL inline
#define RG register
#define gi getint()
#define gc getchar()
#define File(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout)
IL int getint()
{RG int xi=0;RG char ch=gc;bool f=0;while(ch<'0'||ch>'9')ch=='-'?f=1:f,ch=gc;while(ch>='0'&&ch<='9')xi=(xi<<1)+(xi<<3)+ch-48,ch=gc;return f?-xi:xi;
}
IL void pi(int k,char ch=0)
{if(k<0)k=-k,putchar('-');if(k>=10)pi(k/10,0);putchar(k%10+'0');if(ch)putchar(ch);
}
const double eps=1e-9;
inline int dcmp(double a){if(fabs(a)<eps)return 0;return a>0?1:-1;}
struct Point{double x,y;Point(double a=0,double b=0):x(a),y(b){}
}p[2007];
inline bool operator < (const Point &a,const Point &b){return dcmp(a.x-b.x)<0||(!dcmp(a.x-b.x)&&a.y<b.y);
}
inline Point operator + (const Point &a,const Point &b){return (Point){a.x+b.x,a.y+b.y};}
inline Point operator - (const Point &a,const Point &b){return (Point){a.x-b.x,a.y-b.y};}
inline Point operator * (const Point &a,const double &b){return (Point){a.x*b,a.y*b};}
typedef Point Vector;
inline double Dot(const Vector &x,const Vector &y){return x.x*y.x+x.y*y.y;}
inline double Cross(const Vector &x,const Vector &y){return x.x*y.y-x.y*y.x;}
inline int Tubao(Point po[],int n,Point tb[])
{sort(po+1,po+n+1);int top=0;for(int i=1;i<=n;++i){while(top>1&&dcmp(Cross(tb[top]-tb[top-1],po[i]-tb[top-1]))<=0)--top;tb[++top]=po[i];}int tmp=top;for(int i=n-1;i>1;--i){while(top>tmp&&dcmp(Cross(tb[top]-tb[top-1],po[i]-tb[top-1]))<=0)--top;tb[++top]=po[i];}return top;
}
inline double area(Point a,Point b,Point c){return fabs(Cross(b-a,c-a));}
Point tb[2007];
#define nxt(qwq) ((qwq)%m+1)
int main(void)
{int n=gi;for(int i=1;i<=n;++i)scanf("%lf%lf",&p[i].x,&p[i].y);int m=Tubao(p,n,tb);double ans=0;for(int i=1;i<=m;++i){int a=nxt(i),b=nxt(i+2);for(int j=i%m+2;j<=m;++j){while(nxt(a)!=j&&Cross(tb[nxt(a)]-tb[a],tb[j]-tb[i])>0)a=nxt(a);while(nxt(b)!=i&&Cross(tb[nxt(b)]-tb[b],tb[i]-tb[j])>0)b=nxt(b);ans=max(area(tb[a],tb[i],tb[j])+area(tb[b],tb[i],tb[j]),ans);}}printf("%.3lf",ans/2);return 0;
}