机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络

1 贝叶斯方法长久以来，人们对一件事情发生或不发生的概率，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率是多少？”他们会想都不用想，会立马告诉你，取出白球的概率就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果X 的变化而变化。这种频率派的观点长期统治着人们的观念，直到后来一个名叫Thomas Bayes的人物出现。

1.1 贝叶斯方法的提出托马斯·贝叶斯Thomas Bayes（1702-1763）在世时，并不为当时的人们所熟知，很少发表论文或出版著作，与当时学术界的人沟通交流也很少，用现在的话来说，贝叶斯就是活生生一民间学术“屌丝”，可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”，翻译过来则是：机遇理论中一个问题的解。你可能觉得我要说：这篇论文的发表随机产生轰动效应，从而奠定贝叶斯在学术史上的地位。

事实上，上篇论文发表后，在当时并未产生多少影响，在20世纪后，这篇论文才逐渐被人们所重视。对此，与梵高何其类似，画的画生前一文不值，死后价值连城。回到上面的例子：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率θ是多少？”贝叶斯认为取得白球的概率是个不确定的值，因为其中含有机遇的成分。比如，一个朋友创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？你如果对他为人比较了解，而且有方法、思路清晰、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯式的思考方式。

继续深入讲解贝叶斯方法之前，先简单总结下频率派与贝叶斯派各自不同的思考方式：频率派把需要推断的参数θ看做是固定的未知常数，即概率虽然是未知的，但最起码是确定的一个值，同时，样本X 是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本X 的分布；而贝叶斯派的观点则截然相反，他们认为参数是随机变量，而样本X 是固定的，由于样本是固定的，所以他们重点研究的是参数的分布。相对来说，频率派的观点容易理解，所以下文重点阐述贝叶斯派的观点。贝叶斯派既然把看做是一个随机变量，所以要计算的分布，便得事先知道的无条件分布，即在有样本之前（或观察到X之前），有着怎样的分布呢？比如往台球桌上扔一个球，这个球落会落在何处呢？如果是不偏不倚的把球抛出去，那么此球落在台球桌上的任一位置都有着相同的机会，即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为先验分布，或的无条件分布。

至此，贝叶斯及贝叶斯派提出了一个思考问题的固定模式：

上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对θ的认知是先验分布π（θ），在得到新的样本信息X后，人们对的认知为π（θ|X）。

其中，先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决，解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如，某工厂每天都要对产品进行质检，以评估产品的不合格率θ，经过一段时间后便会积累大量的历史资料，这些历史资料便是先验知识，有了这些先验知识，便在决定对一个产品是否需要每天质检时便有了依据，如果以往的历史资料显示，某产品的不合格率只有0.01%，便可视为信得过产品或免检产品，只每月抽检一两次，从而省去大量的人力物力。

而后验分布π（θ|X）一般也认为是在给定样本X的情况下的θ条件分布，而使π（θ|X）达到最大的值θMD称为最大后验估计，类似于经典统计学中的极大似然估计。

综合起来看，则好比是人类刚开始时对大自然只有少得可怜的先验知识，但随着不断观察、实验获得更多的样本、结果，使得人们对自然界的规律摸得越来越透彻。所以，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼。

此外，贝叶斯除了提出上述思考模式之外，还特别提出了举世闻名的贝叶斯定理。

1.2 贝叶斯定理
在引出贝叶斯定理之前，先学习几个定义：条件概率（又称后验概率）就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在B条件下A的概率”。比如，在同一个样本空间Ω中的事件或者子集A与B，如果随机从Ω中选出的一个元素属于B，那么这个随机选择的元素还属于A的概率就定义为在B的前提下A的条件概率，所以：P(A|B) = |A∩B|/|B|，接着分子、分母都除以|Ω|得到

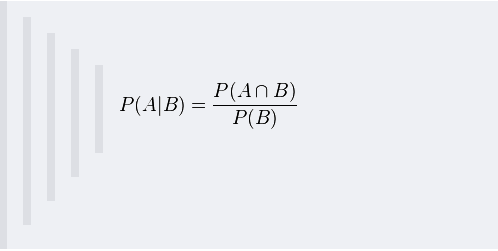
联合概率表示两个事件共同发生的概率。A与B的联合概率表示为

边缘概率（又称先验概率）是某个事件发生的概率。边缘概率是这样得到的：在联合概率中，把最终结果中那些不需要的事件通过合并成它们的全概率，而消去它们（对离散随机变量用求和得全概率，对连续随机变量用积分得全概率），这称为边缘化（marginalization），比如A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

接着，考虑一个问题：P(A|B)是在B发生的情况下A发生的可能性。1、首先，事件B发生之前，我们对事件A的发生有一个基本的概率判断，称为A的先验概率，用P(A)表示；
2、其次，事件B发生之后，我们对事件A的发生概率重新评估，称为A的后验概率，用P(A|B)表示；
3、类似的，事件A发生之前，我们对事件B的发生有一个基本的概率判断，称为B的先验概率，用P(B)表示；
4、同样，事件A发生之后，我们对事件B的发生概率重新评估，称为B的后验概率，用P(B|A)表示。贝叶斯定理便是基于下述贝叶斯公式：

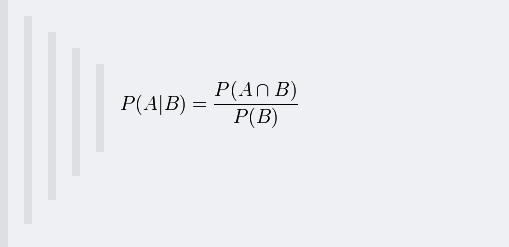
上述公式的推导其实非常简单，就是从条件概率推出。

根据条件概率的定义，在事件B发生的条件下事件A发生的概率是

整理与合并上述两个方程式，便可以得到：

接着，上式两边同除以P(B)，若P(B)是非零的，我们便可以得到贝叶斯定理的公式表达式：

所以，贝叶斯公式可以直接根据条件概率的定义直接推出。即因为P(A,B) = P(A)P(B|A) = P(B)P(A|B)，所以P(A|B) = P(A)P(B|A)  / P(B)。

1.3 应用：拼写检查
经常在网上搜索东西的朋友知道，当你不小心输入一个不存在的单词时，搜索引擎会提示你是不是要输入某一个正确的单词，比如当你在Google中输入“Pythom”时，系统会猜测你的意图：是不是要搜索“Python”，如下图所示：

这叫做拼写检查。根据谷歌一员工写的文章显示，Google的拼写检查基于贝叶斯方法。下面我们就来看看，怎么利用贝叶斯方法，实现"拼写检查"的功能。

用户输入一个单词时，可能拼写正确，也可能拼写错误。如果把拼写正确的情况记做c（代表correct），拼写错误的情况记做w（代表wrong），那么"拼写检查"要做的事情就是：在发生w的情况下，试图推断出c。换言之：已知w，然后在若干个备选方案中，找出可能性最大的那个c，也就是求

而根据贝叶斯定理，有：

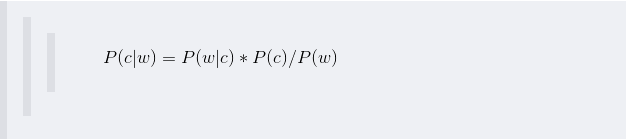
由于对于所有备选的c来说，对应的都是同一个w，所以它们的P(w)是相同的，因此我们只要最大化

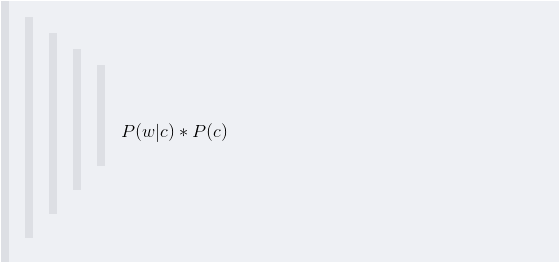
即可。其中：▶ P(c)表示某个正确的词的出现"概率"，它可以用"频率"代替。如果我们有一个足够大的文本库，那么这个文本库中每个单词的出现频率，就相当于它的发生概率。某个词的出现频率越高，P(c)就越大。比如在你输入一个错误的词“pythom”时，系统更倾向于去猜测你可能想输入的词是“python”，而不是“pythow”，因为“python”更常见。▶ P(w|c)表示在试图拼写c的情况下，出现拼写错误w的概率。为了简化问题，假定两个单词在字形上越接近，就有越可能拼错，P(w|c)就越大。举例来说，相差一个字母的拼法，就比相差两个字母的拼法，发生概率更高。你想拼写单词python，那么错误拼成pythom（相差一个字母）的可能性，就比拼成pythow高（相差两个字母）。值得一提的是，一般把这种问题称为“编辑距离”.

所以，我们比较所有拼写相近的词在文本库中的出现频率，再从中挑出出现频率最高的一个，即是用户最想输入的那个词。具体的计算过程及此方法的缺陷请参见这里。

02 贝叶斯网络2.1 贝叶斯网络的定义贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型(directed acyclic graphical model)，是一种概率图模型，于1985年由Judea Pearl首先提出。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓朴结构是一个有向无环图(DAG)。 贝叶斯网络的有向无环图中的节点表示随机变量

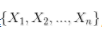
它们可以是可观察到的变量，或隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。

总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。例如，假设节点E直接影响到节点H，即E→H，则用从E指向H的箭头建立结点E到结点H的有向弧(E,H)，权值(即连接强度)用条件概率P(H|E)来表示，如下图所示：

简言之，把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。其主要用来描述随机变量之间的条件依赖，用圈表示随机变量(random variables)，用箭头表示条件依赖(conditional dependencies)。令G = (I,E)表示一个有向无环图(DAG)，其中I代表图形中所有的节点的集合，而E代表有向连接线段的集合，且令X = (Xi)i ∈ I为其有向无环图中的某一节点i所代表的随机变量，若节点X的联合概率可以表示成：

则称X为相对于一有向无环图G 的贝叶斯网络，其中，pa(i)表示节点i之“因”，或称pa(i)是i的parents（父母）。 此外，对于任意的随机变量，其联合概率可由各自的局部条件概率分布相乘而得出：

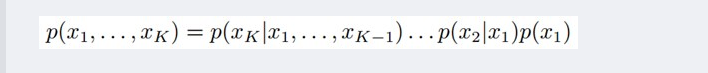
如下图所示，便是一个简单的贝叶斯网络：

因为a导致b，a和b导致c，所以有

2.2 贝叶斯网络的3种结构形式

给定如下图所示的一个贝叶斯网络：

从图上可以比较直观的看出：1. x1,x2,…x7的联合分布为

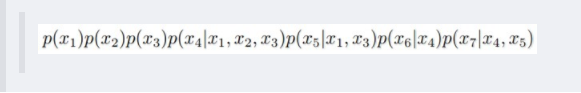
2. x1和x2独立（对应head-to-head）；3. x6和x7在x4给定的条件下独立（对应tail-to-tail）。根据上图，第1点可能很容易理解，但第2、3点中所述的条件独立是啥意思呢？其实第2、3点是贝叶斯网络中3种结构形式中的其中二种。为了说清楚这个问题，需要引入D-Separation（D-分离）这个概念。D-Separation是一种用来判断变量是否条件独立的图形化方法。换言之，对于一个DAG(有向无环图)E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

2.2.1 形式1：head-to-head贝叶斯网络的第一种结构形式如下图所示：

所以有：P(a,b,c) = P(a)*P(b)*P(c|a,b)成立，化简后可得：

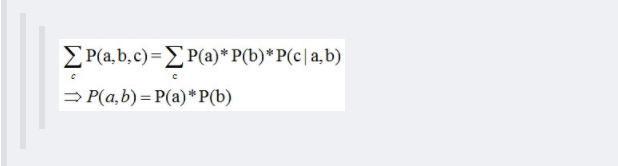
即在c未知的条件下，a、b被阻断(blocked)，是独立的，称之为head-to-head条件独立，对应本节中最开始那张图中的“x1、x2独立”。2.2.2 形式2：tail-to-tail

贝叶斯网络的第二种结构形式如下图所示

考虑c未知，跟c已知这两种情况：1、在c未知的时候，有：P(a,b,c)=P(c)*P(a|c)*P(b|c)，此时，没法得出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。2、在c已知的时候，有：P(a,b|c)=P(a,b,c)/P(c)，然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入式子中，得到：P(a,b|c)=P(a,b,c)/P(c) = P(c)*P(a|c)*P(b|c) / P(c) = P(a|c)*P(b|c)，即c已知时，a、b独立。所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为tail-to-tail条件独立，对应本节中最开始那张图中的“x6和x7在x4给定的条件下独立”。

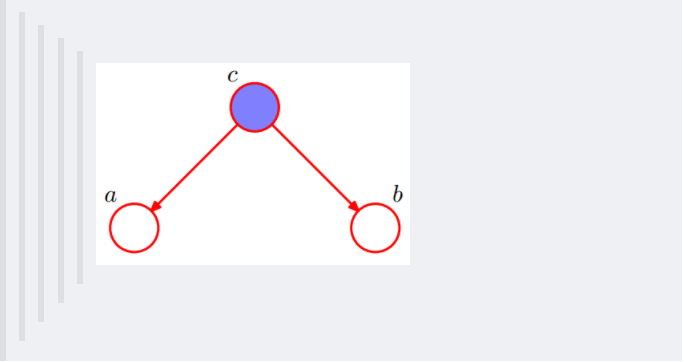
2.2.3 形式3：head-to-tail贝叶斯网络的第三种结构形式如下图所示：

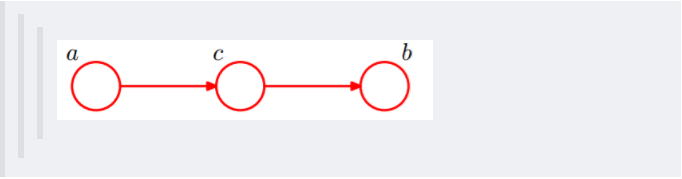
还是分c未知跟c已知这两种情况：1、c未知时，有：P(a,b,c)=P(a)*P(c|a)*P(b|c)，但无法推出P(a,b) = P(a)P(b)，即c未知时，a、b不独立。2、c已知时，有：P(a,b|c)=P(a,b,c)/P(c)，且根据P(a,c) = P(a)*P(c|a) = P(c)*P(a|c)，可化简得到：

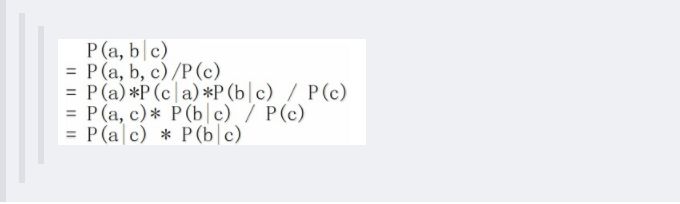
所以，在c给定的条件下，a，b被阻断(blocked)，是独立的，称之为head-to-tail条件独立。

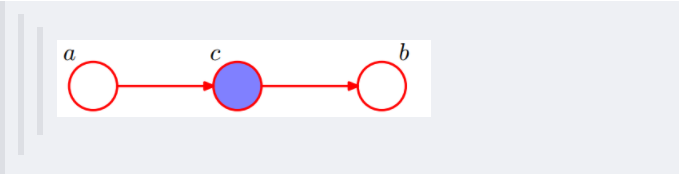
  插一句：这个head-to-tail其实就是一个链式网络，如下图所示：

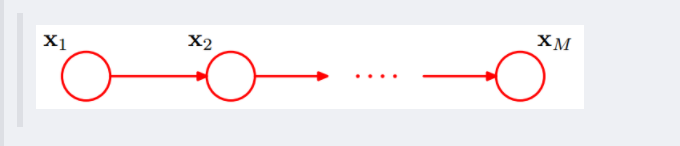
根据之前对head-to-tail的讲解，我们已经知道，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。意味着啥呢？意味着：xi+1的分布状态只和xi有关，和其他变量条件独立。通俗点说，当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。且有：

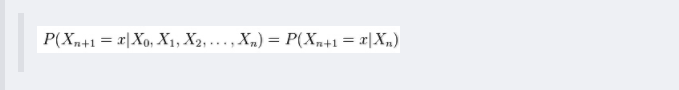
接着，将上述结点推广到结点集，则是：对于任意的结点集A，B，C，考察所有通过A中任意结点到B中任意结点的路径，若要求A，B条件独立，则需要所有的路径都被阻断(blocked)，即满足下列两个前提之一：

A和B的“head-to-tail型”和“tail-to-tail型”路径都通过C；A和B的“head-to-head型”路径不通过C以及C的子孙；最后，举例说明上述D-Separation的3种情况（即贝叶斯网络的3种结构形式），则是如下图所示：

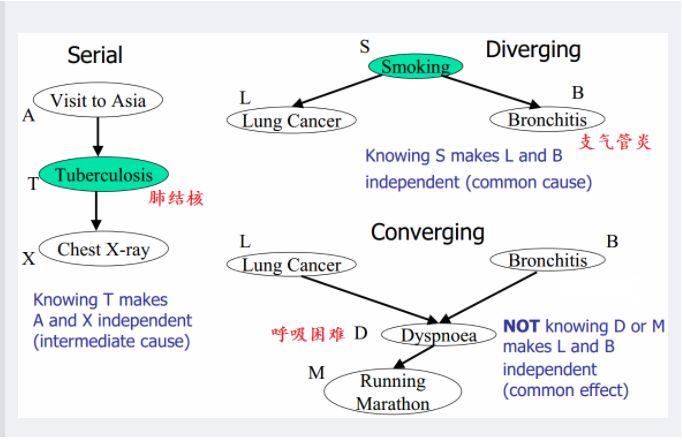
上图中左边部分是head-to-tail，给定 T 时，A 和 X 独立；右边部分的右上角是tail-to-tail，给定S时，L和B独立；右边部分的右下角是head-to-head，未给定D时，L和B独立。2.3 贝叶斯网络的实例给定如下图所示的贝叶斯网络：

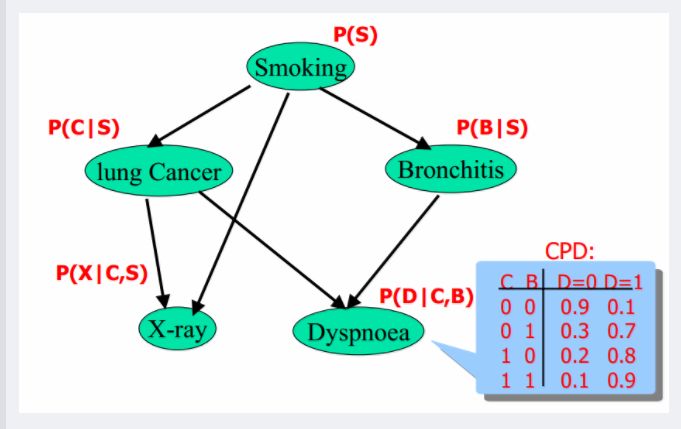
其中，各个单词、表达式表示的含义如下：▶ smoking表示吸烟，其概率用P(S)表示，lung Cancer表示的肺癌，一个人在吸烟的情况下得肺癌的概率用P(C|S)表示，X-ray表示需要照医学上的X光，肺癌可能会导致需要照X光，吸烟也有可能会导致需要照X光（所以smoking也是X-ray的一个因），所以，因吸烟且得肺癌而需要照X光的概率用P(X|C,S)表示。▶ Bronchitis表示支气管炎，一个人在吸烟的情况下得支气管炎的概率用P(B|S)，dyspnoea表示呼吸困难，支气管炎可能会导致呼吸困难，肺癌也有可能会导致呼吸困难（所以lung Cancer也是dyspnoea的一个因），因吸烟且得了支气管炎导致呼吸困难的概率用P(D|C,B)表示。lung Cancer简记为C，Bronchitis简记为B，dyspnoea简记为D，且C = 0表示lung Cancer不发生的概率，C = 1表示lung Cancer发生的概率，B等于0（B不发生）或1（B发生）也类似于C，同样的，D=1表示D发生的概率，D=0表示D不发生的概率，便可得到dyspnoea的一张概率表，如上图的最右下角所示。

2.4 因子图回到2.3节中那个实例上，如下图所示：

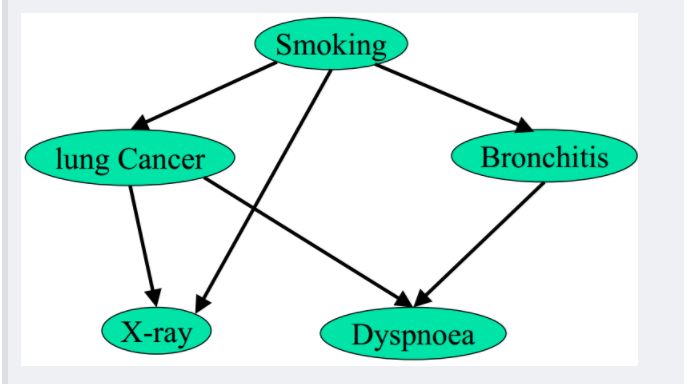
对于上图，在一个人已经呼吸困难（dyspnoea）的情况下，其抽烟（smoking）的概率是多少呢？即：

咱们来一步步计算推导下：

解释下上述式子推导过程：1、第二行：对联合概率关于b,x,c求和（在d=1的条件下），从而消去b,x,c，得到s和d=1的联合概率。2、第三行：最开始，所有变量都在sigma(d=1,b,x,c)的后面（sigma表示对“求和”的称谓），但由于P(s)和“d=1,b,x,c”都没关系，所以，可以提到式子的最前面。而且P(b|s)和x、c没关系，所以，也可以把它提出来，放到sigma(b)的后面，从而式子的右边剩下sigma(x)和sigma(c)。此外，图中Variable elimination表示的是变量消除的意思。为了更好的解决此类问题，咱们得引入因子图的概念。2.4.1 因子图的定义wikipedia上是这样定义因子图的：将一个具有多变量的全局函数因子分解，得到几个局部函数的乘积，以此为基础得到的一个双向图叫做因子图（Factor Graph）。

比如，假定对于函数，有下述式子成立：

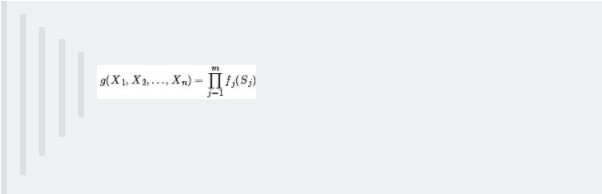
通俗来讲，所谓因子图就是对函数进行因子分解得到的一种概率图。一般内含两种节点：变量节点和函数节点。我们知道，一个全局函数通过因式分解能够分解为多个局部函数的乘积，这些局部函数和对应的变量关系就体现在因子图上。

（未完待续）

机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络相关推荐

贝叶斯方法和贝叶斯网络
从贝叶斯方法谈到贝叶斯网络 0 引言看到July的这篇文章,觉得写得很好,所以转载过来,留着慢慢看.原地址:https://blog.csdn.net/v_july_v/article/detail ...
LeetCode题库整理【Java】—— 3 无重复字符的最长子串
LeetCode题库整理[Java] ## 3 无重复字符的最长子串题目:给定一个字符串,请你找出其中不含有重复字符的最长子串的长度. 示例 1: 输入: "abcabcbb" ...
LeetCode题库整理【Java】—— 2 两数相加
LeetCode题库整理[Java] 2.两数相加题目:给出两个非空的链表用来表示两个非负的整数.其中,它们各自的位数是按照逆序的方式存储的,并且它们的每个节点只能存储一位数字. 如果, ...
LeetCode题库整理【Java】—— 7整数反转
LeetCode题库整理[Java] 7.整数反转题目:给出一个32位的有符号整数,你需要将这个这个整数中每位上的数字进行反转. 示例1: 输入: 123 输出: 321 示例2: 输入: -123 ...
LeetCode题库整理【Java】—— 1两数之和
LeetCode题库整理[Java] 1.两数之和题目:给定一个整数数组和一个目标值,找出数组中和为目标值的两个数.你可以假设每个输入只对应一种答案,且同样的元素不能被重复利用. 示例: 给定 nu ...
HCIP考试心得，题库整理
HCIP考试心得,题库整理. 本人整理的题库,结合了多版本题库,去重,修正错误,加入注解, 汇总而成,为方便刷题,进行了分类.需要的可以联系.qq:403391198,
太理java题库_2020年Java题库整理
2020年Java题库整理(WUST) 前言:去我的个人博客阅读效果更好哟. 知识点整理: 1.Java 语言具有跨平台性, 是一种面向对象的语言,程序具有可移植性,不可多继承. 2.Java的标准版 ...
mysql认证考试6_Mysql 8.0 OCP认证考试原题题库整理-第6题（CUUG内部资料）
Mysql 8.0 OCP认证考试原题题库整理(CUUG内部资料)-第6题 Choose the best answer. You are having performance issues with ...
mysql ocp 认证题库_Mysql 8.0 OCP认证考试原题题库整理（CUUG内部资料）-第1题
Mysql 8.0 OCP认证考试原题题库整理(CUUG内部资料)-第1题 1.Choose the best answer. Examine these statements and output: ...

机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络

机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络相关推荐

最新文章

热门文章

机器学习题库整理 通俗理解贝叶斯方法和贝叶斯网络

机器学习题库整理 通俗理解贝叶斯方法和贝叶斯网络相关推荐

最新文章

热门文章

机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络

机器学习题库整理通俗理解贝叶斯方法和贝叶斯网络相关推荐