【一文带你读懂机器学习】逻辑回归原理

一．逻辑回归简述

在【一文带你读懂机器学习】线性回归原理中我们已经详细的对线性回归的原理进行阐述，线性回归通常是用来解决回归问题的。

然而，我们现实生活中遇到的不仅有回归任务，同样我们也会遇到分类任务，比如根据邮件标题或者邮件的内容预测邮件是否为垃圾邮件，根据患者的病历预测肿瘤患者的疾病是阴性的还是阳性的等等。

线性回归一般能够很好解决回归问题的，但是往往不能很好解决分类任务。

如下图，我们拿Andrew Ng吴恩达老师的机器学习的课中的肿瘤预测的例子来看看，这个数据集中，横轴表示肿瘤的大小，纵轴上，我标出1和0表示是或者不是恶性肿瘤。我们之前见过的肿瘤，如果是恶性则记为1，用X表示，不是恶性，或者说良性记为0，用 O 表示。

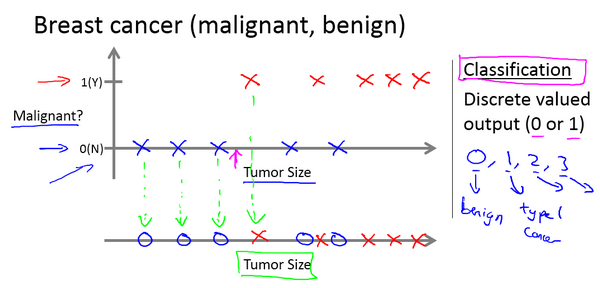
通常我们最为基础的分类模型为逻辑回归即logistics回归。

逻辑回归是应用非常广泛的一个分类机器学习算法，它将数据拟合到一个logit函数(或者叫做logistic函数)中，从而能够完成对事件发生的概率进行预测。

二．逻辑回归原理

逻辑回归的原理和线性回归的原理是相似的，按照我自己的理解，可以简单的描述为这样的过程：

（1）找一个合适的假设函数（Andrew Ng的公开课中称为hypothesis）

一般表示为h函数，该函数就是我们需要找的分类函数，它用来预测输入数据的判断结果。

在线性回归中，这个假设函数的公式为hθ(x)=θXh_\theta(x) = \theta Xhθ(x)=θX

而在逻辑回归中，我们的假设函数为hθ(x)=11+e−θXh_\theta(x) = \frac{1}{1+e^{-\theta X}}hθ(x)=1+e−θX1

在后面，我们将对该假设函数进行说明

（2）构造一个Cost函数（损失函数）

该函数表示预测的输出（h）与训练数据类别（y）之间的偏差。

在线性回归一文中我们已经知道其为：J(θ)=12∑i=1m(hθ(x(i))−y(i))2J(\theta)= \frac{1}{2}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2J(θ)=21∑i=1m(hθ(x(i))−y(i))2

而逻辑回归中其损失函数为：J(θ)=−1m∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))J(\theta)= -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})))J(θ)=−m1∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))

在后面我们将对该假设函数进行推导

（3）利用梯度下降法，求得使得损失函数最小时候的θ\thetaθ值

显然，J(θ)函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要做的是找到J(θ)函数的最小值。

找函数的最小值有不同的方法，逻辑回归实现时有的是梯度下降法（Gradient Descent）。

三.逻辑回归的假设函数

3.1假设函数的说明

在上一部分我们讲到逻辑回归的假设函数为
z=θXz =\theta X z=θX
hθ(x)=11+e−zh_\theta(x) = \frac{1}{1+e^{-z}}hθ(x)=1+e−z1

其表示的含义如下：hθ(x)＝p(y(i)=1∣x(i);θ)h_\theta(x) ＝p(y^{(i)}=1|x^{(i)};\theta)hθ(x)＝p(y(i)=1∣x(i);θ)

即在给定θ\thetaθ值的情况下，当我们已知样本的属性值x(i)x^{(i)}x(i)的情况下，y(i)=1y^{(i)}=1y(i)=1的条件概率

例如hθ(x)＝0.7h_\theta(x) ＝0.7hθ(x)＝0.7，如果对于给定x(i)x^{(i)}x(i)的，通过已经确定的参数θ\thetaθ计算得出，则表示有70%的几率为正向类，相应地为负向类的几率为1-0.7=0.3。

我们来看看其函数图像如下：

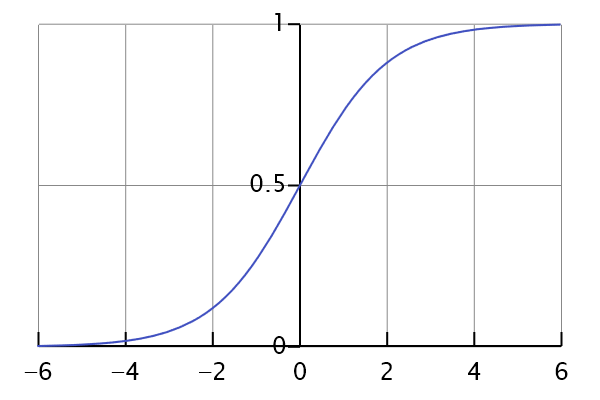
从图像中我们可以看到，它平滑地从０走向１，并且曲线与纵轴的交点的值为0.5

在zzz这里是一个实数，下面我们对于zzz的两种情况来分析这个函数图像：

hθ(x)=11+e−zh_\theta(x) = \frac{1}{1+e^{-z}}hθ(x)=1+e−z1

①ｚ非常大，趋近于正无穷：

如果ｚ非常大，趋近于正无穷,那么e−ze^{-z}e−z将会接近于0，

关于hθ(x)h_\theta(x)hθ(x)将会近似等于1除以1加上某个非常接近于0的项，那么hθ(x)h_\theta(x)hθ(x)函数会非常接近1。

②ｚ非常小，趋近于负无穷：

如果ｚ非常小，趋近于负无穷,那么e−ze^{-z}e−z将会接近于正无穷，

关于hθ(x)h_\theta(x)hθ(x)将会近似等于1除以1加上某个非常接近于大的数，那么hθ(x)h_\theta(x)hθ(x)函数会非常接近０。

3.２决策边界(decision boundary)

3.２.1线性决策边界

现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。

在逻辑回归中，我们预测：

当hθ(x)>0.5h_\theta(x) >0.5hθ(x)>0.5 时，ｙ＝１ｙ＝１ｙ＝１，为正例

当hθ(x)<0.5h_\theta(x) <0.5hθ(x)<0.5 时，ｙ＝０ｙ＝０ｙ＝０，为负例

根据上面绘制出的 S 形函数图像，我们知道当

z=0z = 0z=0 时，hθ(x)=0.5h_\theta(x) =0.5hθ(x)=0.5

z>0z > 0z>0 时，hθ(x)>0.5h_\theta(x) >0.5hθ(x)>0.5

z<0z < 0z<0 时，hθ(x)<0.5h_\theta(x) < 0.5hθ(x)<0.5

又$z =\theta X ,即当,即当,即当\theta X>0时，我们预测时，我们预测时，我们预测y=1,当,当,当\theta X<0时，我们预测时，我们预测时，我们预测y=0$

现在我们假设有一个模型

并且参数θ\thetaθ 是向量[−311]\begin{bmatrix} -3 & 1 & 1 \end{bmatrix}[−311]即θ1=−3\theta1= -3θ1=−3,θ2=1\theta2= 1θ2=1,θ3=1\theta3= 1θ3=1。则

当−3+x1+x2≥0-3+x_1+x_2\geq 0−3+x1+x2≥0时，，模型将预测y=1y=1y=1 。

当−3+x1+x2≤0-3+x_1+x_2\leq 0−3+x1+x2≤0时，，模型将预测y=0y=0y=0 。

我们可以绘制直线−3+x1+x2=0-3+x_1+x_2=0−3+x1+x2=0，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。

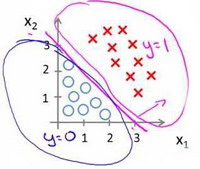
这条线我们称之为决策边界(decision boundary)。

3.２.２非线性决策边界

假如我们的数据我们分布如图所示，无法用一条直线将其分开，即非线性可分的话

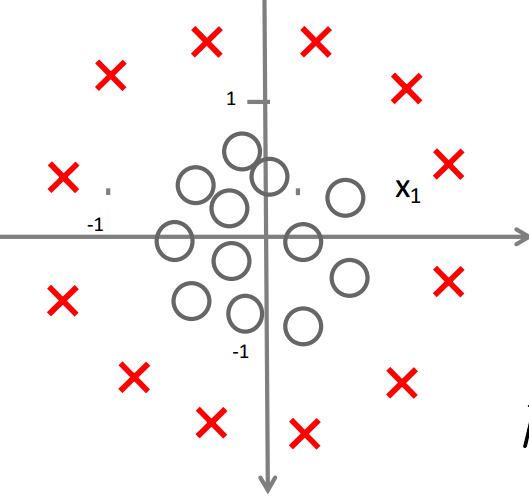
怎样的模型才能很好的将二者区分开来呢？

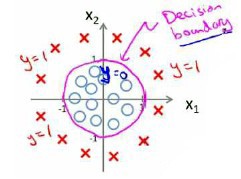
因为需要用曲线才能分隔y=0y=0y=0的区域和y=1y=1y=1的区域，

我们需要二次方特征hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x22)：

并且参数θ\thetaθ 是向量[−１００1]\begin{bmatrix} -１ & ０ & ０& 1 \end{bmatrix}[−１００1]即θ1=−1\theta1= -1θ1=−1,θ2=0\theta2= 0θ2=0,θ3=0\theta3= 0θ3=0,θ3=1\theta3= 1θ3=1。则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。

我们推广之，对于更复杂的模型hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x12x2+θ5x12x22+θ6x13x2+...)h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_1^2x_2+\theta_5x_1^2x_2^2+\theta_6x_1^3x_2+...)hθ(x)=g(θ0+θ1x1+θ2x2+θ3x12+θ4x12x2+θ5x12x22+θ6x13x2+...)

我们可同样可以找到其判定边界为θ0+θ1x1+θ2x2+θ3x12+θ4x12x2+θ5x12x22+θ6x13x2+...＝０\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_1^2x_2+\theta_5x_1^2x_2^2+\theta_6x_1^3x_2+...＝０θ0+θ1x1+θ2x2+θ3x12+θ4x12x2+θ5x12x22+θ6x13x2+...＝０

四.逻辑回归的损失函数

4.1 逻辑回归的损失函数概述

在线性回归一文中，我们已经知道我们的损失函数为

J(θ)=12∑i=1m(hθ(x(i))−y(i))2J(\theta)= \frac{1}{2}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2J(θ)=21i=1∑m(hθ(x(i))−y(i))2

但是问题在于，当我们将hθ(x)=11+e−θXh_\theta(x) = \frac{1}{1+e^{-\theta X}}hθ(x)=1+e−θX1带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）。函数图像大致如下

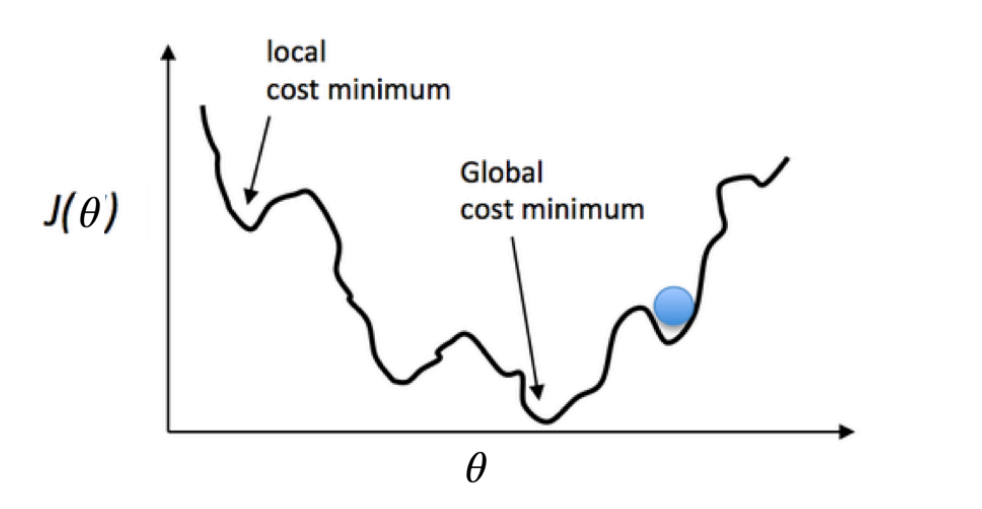
我们很容易得到局部最优解，而无法得到全局最优解。

我们重新定义逻辑回归的代价函数为：

J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})J(θ)=m1i=1∑mCost(hθ(x(i)),y(i))

其中
KaTeX parse error: Got function '\newline' as argument to '\left' at position 1: \̲n̲e̲w̲l̲i̲n̲e̲

其函数图像如下

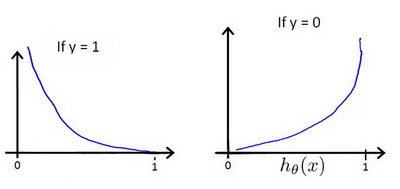
我们可以将损失函数简化如下：

J(θ)=−1m∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))J(\theta)= -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)})))J(θ)=−m1i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))

此函数即为逻辑回归的损失函数

为什么要用这个函数作为逻辑损失函数？

当我们使用平方误差作为损失函数的时候，你会想要让这个误差尽可能地小。

对于这个逻辑回归损失函数，我们也想让它尽可能地小，为了更好地理解这个损失函数怎么起作用，我们举两个例子：

当标签y(i)=0y^{(i)}=0y(i)=0时，J(θ)=−1m∑i=1m(log(1−hθ(x(i))))J(\theta)= -\frac{1}{m}\sum_{i=1}^{m}(log(1-h_\theta(x^{(i)})))J(θ)=−m1∑i=1m(log(1−hθ(x(i))))，如果想要损失函数J(θ)J(\theta)J(θ)尽可能得大，那么y(i)y^{(i)}y(i)就要尽可能小，因为hθh_\thetahθ函数取值范围为[0,1]\left[0,1\right][0,1]，所以会无限接近于０。

当标签y(i)=1y^{(i)}=1y(i)=1时，J(θ)=−1m∑i=1m(log(hθ(x(i))))J(\theta)= -\frac{1}{m}\sum_{i=1}^{m}(log(h_\theta(x^{(i)})))J(θ)=−m1∑i=1m(log(hθ(x(i))))，如果想要损失函数J(θ)J(\theta)J(θ)尽可能得小，那么y(i)y^{(i)}y(i)就要尽可能大，因为hθh_\thetahθ函数取值范围为[0,1]\left[0,1\right][0,1]，所以会无限接近于1。

4.1 逻辑回归的损失函数推导（极大似然估计）

在线性回归中，我们已经利用极大似然估计推导过其损失函数，那么对于逻辑回归，我们同样用极大似然估计对其进行推导。

我们之前已经说到表示的意思为hθ(x)h_\theta(x)hθ(x)在给定θ\thetaθ值的情况下，当我们已知样本的属性值x(i)x^{(i)}x(i)的情况下，y(i)=1y^{(i)}=1y(i)=1的条件概率，则

p(y(i)=1∣x(i);θ)＝hθ(x)p(y^{(i)}=1|x^{(i)};\theta)＝h_\theta(x)p(y(i)=1∣x(i);θ)＝hθ(x)
p(y(i)=０∣x(i);θ)＝１－hθ(x)p(y^{(i)}=０|x^{(i)};\theta)＝１－h_\theta(x)p(y(i)=０∣x(i);θ)＝１－hθ(x)

因此，我们可以将以上两式子整合为

p(y(i)∣x(i);θ)＝hθ(x)y(i)(１－hθ(x))1−y(i)p(y^{(i)}|x^{(i)};\theta)＝h_\theta(x)^{y^{(i)}}(１－h_\theta(x))^{{1-y^{(i)}}}p(y(i)∣x(i);θ)＝hθ(x)y(i)(１－hθ(x))1−y(i)

取似然函数为：

L(θ)=∏i=1mhθ(x)y(i)(１－hθ(x))1−y(i)L(\theta) = \prod_{i=1}^{m}h_\theta(x)^{y^{(i)}}(１－h_\theta(x))^{{1-y^{(i)}}}L(θ)=i=1∏mhθ(x)y(i)(１－hθ(x))1−y(i)

为了运算方便，我们同样将两边取logloglog，将连乘转化为连加

我们记

l(θ)=logL(θ)l(\theta)=logL(\theta) l(θ)=logL(θ)

则

l(θ)=log∏i=1mhθ(x)y(i)(１－hθ(x))1−y(i)=∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))\begin{aligned} l(\theta)　&= log\prod_{i=1}^{m}h_\theta(x)^{y^{(i)}}(１－h_\theta(x))^{{1-y^{(i)}}}\\\\ &= \sum_{i=1}^{m}(y^{(i)}log h_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))) \end{aligned}l(θ)　=logi=1∏mhθ(x)y(i)(１－hθ(x))1−y(i)=i=1∑m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i))))

最大似然估计就是要求得使l(θ)l(\theta)l(θ)取最大值时的θ\thetaθ的值。

我们知道损失函数的定义是预测值与真实值的差。损失函数越小，模型越好。

因此我们对l(θ)l(\theta)l(θ)取负系数，并取平均值，因此乘一个负的系数-1/m，就得到逻辑回归的损失函数：

五．梯度下降法求解Ｊ(θ)Ｊ(\theta)Ｊ(θ)最小值

对于逻辑回归的损失函数极小化求θ\thetaθ值，同样，我们使用的是梯度下降法。

关于梯度下降法，详情请看我们的线性回归一课

我们的损失函数如下:
J(θ)=−1m∑i=1m[y(i)log⁡(hθ(x(i)))+(1−y(i))log⁡(1−hθ(x(i)))]J(\theta)=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]

如果我们要最小化这个关于的函数值，这就是我们通常用的梯度下降法的模板。

如果我们要最小化这个关于θ\thetaθ的函数值，这就是我们通常用的梯度下降法的公式：

θj:=θj−α∂∂θjJ(θ)=θj−α1m∑i=1m(hθ(x(i)−y(i))xj(i)\theta_{j} :=\theta_{j}-\alpha \frac{\partial}{\partial_{\theta_{j}}} J(\theta)=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}-y^{(i)}\right) x_{j}^{(i)}\right. θj:=θj−α∂θj∂J(θ)=θj−αm1i=1∑m(hθ(x(i)−y(i))xj(i)

六．二分类与多分类

逻辑回归通常是一个传统的二分类模型，但是它同样可以用于多分类任务。

其基本思想是：将多分类任务拆分成若干个二分类任务，然后对每个二分类任务训练一个模型，最后将多个模型的结果进行集成以获得最终的分类结果。

一般来说，可以采取的拆分策略有one vs one策略和one vs rest策略

6.1 one vs one策略

假设我们有NNN个类别，该策略基本思想就是不同类别两两之间训练一个分类器。

这时我们一共会训练出CN2C_{N}^{2}CN2种不同的分类器。

在预测时，我们将样本提交给所有的分类器，一共会获得N(N−1)N(N−1)N(N−1)个结果，最终结果通过投票产生。

6.1 one vs one策略

该策略基本思想就是：将第iii种类型的所有样本作为正例，将剩下的所有样本作为负例，进行训练得到一个分类器。

假设有N种类别

正例：第iii种类型的所有样本。

负例：剩下的除了第iii类的（N−1）（N-1）（N−1）类的所有样本、

这样我们就一共可以得到NNN个分类器。

在预测时，我们将样本提交给所有的分类器，一共会获得NNN个结果，我们选择其中概率值最大的那个作为最终分类结果。