Ellipse（椭圆）

原滋原味的英文介绍，挺有意思！

http://mathworld.wolfram.com/Ellipse.html

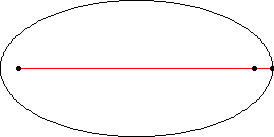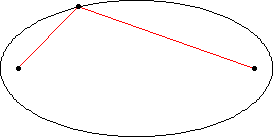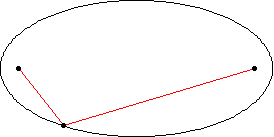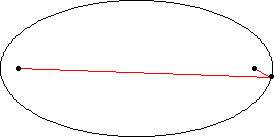
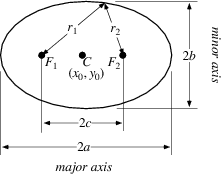
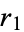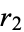An ellipse is a curve that is the locus of all points in the plane the sum of whose distances and from two fixed points 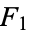and 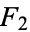(the foci) separated by a distance of 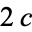is a given positive constant 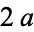(Hilbert and Cohn-Vossen 1999, p. 2). This results in the two-center bipolar coordinate equation

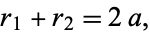
(1)

where 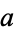is the semimajor axis and the origin of the coordinate system is at one of the foci. The corresponding parameter 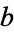is known as the semiminor axis.

The ellipse is a conic section and a Lissajous curve.

An ellipse can be specified in the Wolfram Language using Circle[x, y, a, b].

If the endpoints of a segment are moved along two intersecting lines, a fixed point on the segment (or on the line that prolongs it) describes an arc of an ellipse. This is known as the trammel construction of an ellipse (Eves 1965, p. 177).

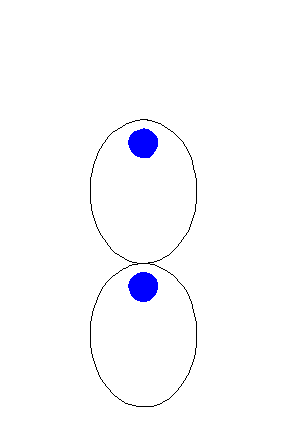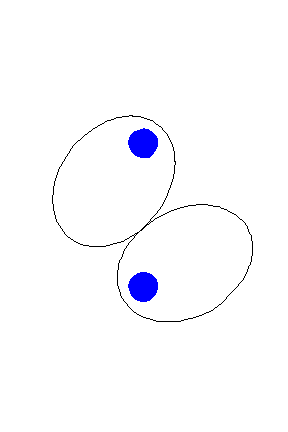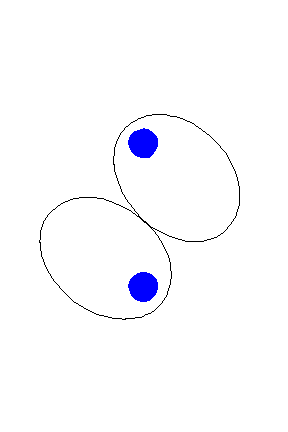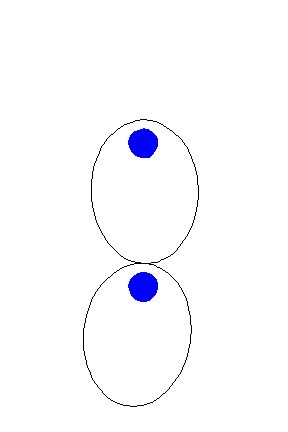
It is possible to construct elliptical gears that rotate smoothly against one another (Brown 1871, pp. 14-15; Reuleaux and Kennedy 1876, p. 70; Clark and Downward 1930; KMODDL).

The ellipse was first studied by Menaechmus, investigated by Euclid, and named by Apollonius. The focus and conic section directrix of an ellipse were considered by Pappus. In 1602, Kepler believed that the orbit of Mars was oval; he later discovered that it was an ellipse with the Sun at one focus. In fact, Kepler introduced the word "focus" and published his discovery in 1609. In 1705 Halley showed that the comet now named after him moved in an elliptical orbit around the Sun (MacTutor Archive). An ellipse rotated about its minor axis gives an oblate spheroid, while an ellipse rotated about its major axis gives a prolate spheroid.

A ray of light passing through a focus will pass through the other focus after a single bounce (Hilbert and Cohn-Vossen 1999, p. 3). Reflections not passing through a focus will be tangent to a confocal hyperbola or ellipse, depending on whether the ray passes between the foci or not.

Let an ellipse lie along the x-axis and find the equation of the figure (1) where and are at 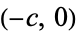and 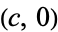. In Cartesian coordinates,

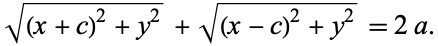
(2)

Bring the second term to the right side and square both sides,

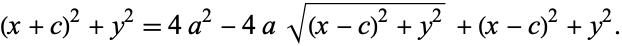
(3)

Now solve for the square root term and simplify

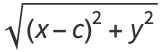
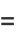
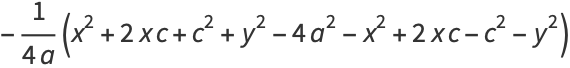
			(4)
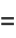
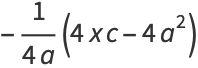
			(5)
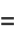
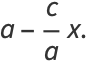
			(6)

Square one final time to clear the remaining square root,

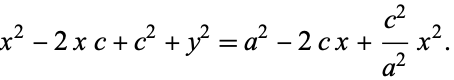
(7)

Grouping the 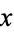terms then gives

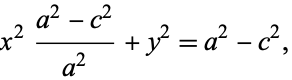
(8)

which can be written in the simple form

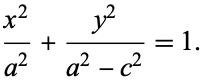
(9)

Defining a new constant

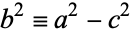
(10)

puts the equation in the particularly simple form

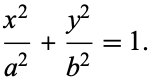
(11)

The parameter 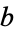is called the semiminor axis by analogy with the parameter 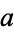, which is called the semimajor axis (assuming 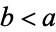). The fact that 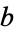as defined above is actually the semiminor axis is easily shown by letting 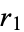and 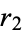be equal. Then two right triangles are produced, each with hypotenuse 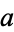, base 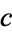, and height 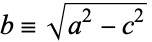. Since the largest distance along the minor axis will be achieved at this point, 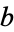is indeed the semiminor axis.

If, instead of being centered at (0, 0), the center of the ellipse is at (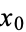, 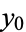), equation (◇) becomes

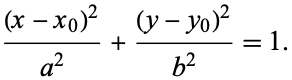
(12)

As can be seen from the Cartesian equation for the ellipse, the curve can also be given by a simple parametric form analogous to that of a circle, but with the 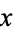and 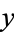coordinates having different scalings,

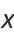
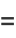
			(13)
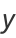
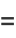
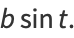
			(14)

The general quadratic curve

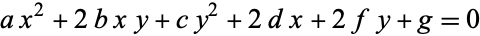
(15)

is an ellipse when, after defining

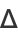
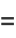
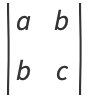
			(16)
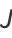
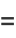
			(17)
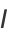
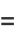
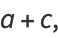
			(18)

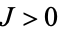, , and 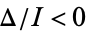. Also assume the ellipse is nondegenerate (i.e., it is not a circle, so 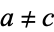, and we have already established is not a point, since 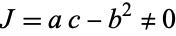). In that case, the center of the ellipse 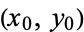is given by

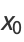
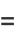
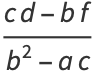
			(19)
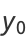
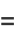
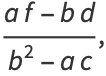
			(20)

the semi-axis lengths are

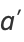
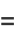
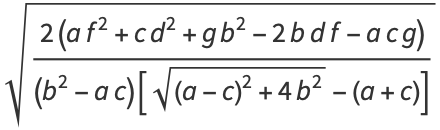
			(21)
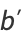
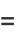
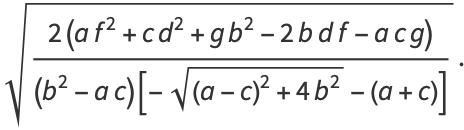
			(22)

and the counterclockwise angle of rotation from the 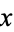-axis to the major axis of the ellipse is

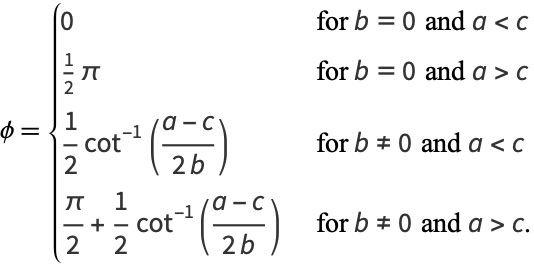
(23)

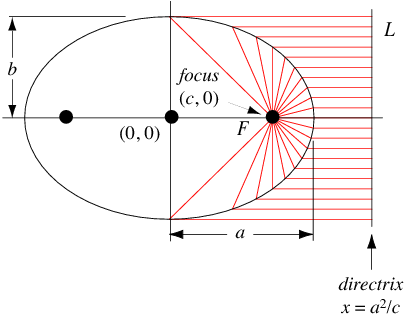
The ellipse can also be defined as the locus of points whose distance from the focus is proportional to the horizontal distance from a vertical line known as the conic section directrix, where the ratio is 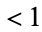. Letting 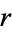be the ratio and 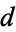the distance from the center at which the directrix lies, then in order for this to be true, it must hold at the extremes of the major and minor axes, so

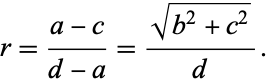
(24)

Solving gives

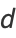
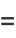
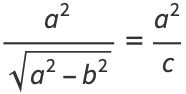
			(25)
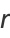
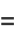
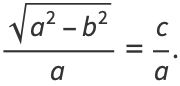
			(26)

The focal parameter of the ellipse is

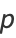
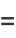
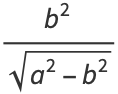
			(27)
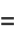
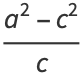
			(28)
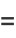
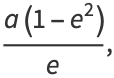
			(29)

where 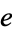is a characteristic of the ellipse known as the eccentricity, to be defined shortly.

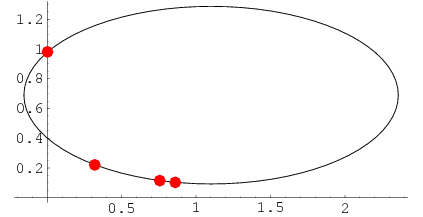
An ellipse whose axes are parallel to the coordinate axes is uniquely determined by any four non-concyclic points on it, and the ellipse passing through the four points 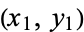, , 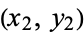, 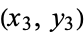and 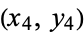has equation

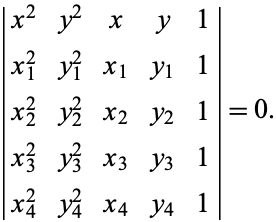
(30)

Let four points on an ellipse with axes parallel to the coordinate axes have angular coordinates 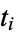for 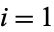, 2, 3, and 4. Such points are concyclic when

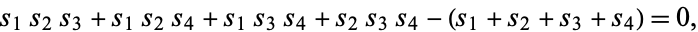
(31)

where the intermediate variable 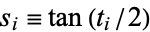has been defined (Berger et al. 1984; Trott 2006, pp. 39-40). Rather surprisingly, this same relationship results after simplification of the above where 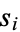is now interpreted as 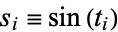. An equivalent, but more complicated, condition is given by

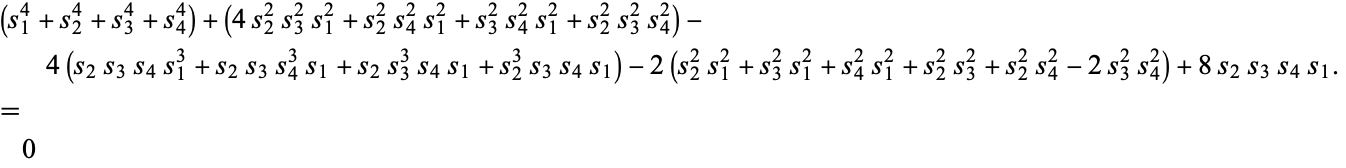
(32)

Like hyperbolas, noncircular ellipses have two distinct foci and two associated directrices, each conic section directrix being perpendicular to the line joining the two foci (Eves 1965, p. 275).

Define a new constant 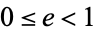called the eccentricity (where 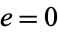is the case of a circle) to replace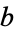

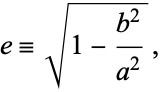
(33)

from which it follows that

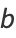
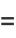
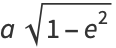
			(34)
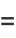
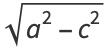
			(35)
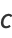
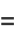
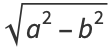
			(36)
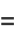
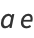
			(37)
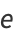
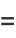
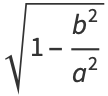
			(38)
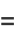
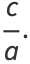
			(39)

The eccentricity can therefore be interpreted as the position of the focus as a fraction of the semimajor axis.

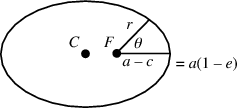
If 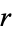and 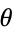are measured from a focus 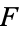instead of from the center 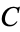(as they commonly are in orbital mechanics) then the equations of the ellipse are

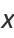
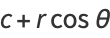
			(40)
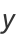
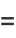
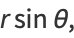
			(41)

and (◇) becomes

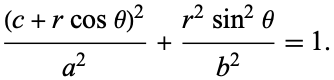
(42)

Clearing the denominators gives

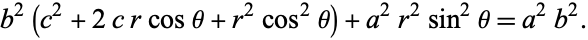
(43)

Substituting in 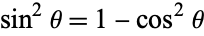gives

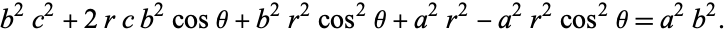
(44)

Plugging in to re-express 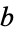and 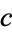in terms of 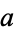and ,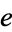

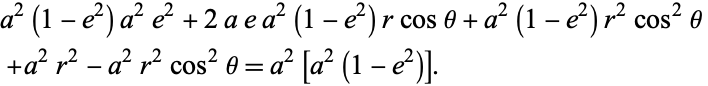
(45)

Dividing by 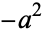and simplifying gives

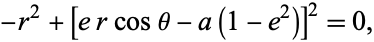
(46)

which can be solved for 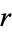to obtain

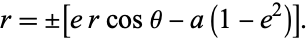
(47)

The sign can be determined by requiring that 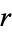must be positive. When 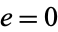, (47) becomes 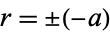, but since 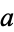is always positive, we must take the negative sign, so (47) becomes

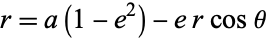
(48)

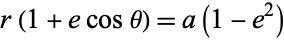
(49)

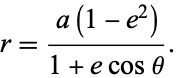
(50)

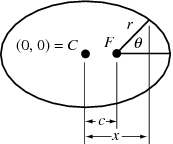
The distance from a focus to a point with horizontal coordinate 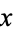(where the origin is taken to lie at the center of the ellipse) is found from

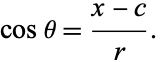
(51)

Plugging this into (50) yields

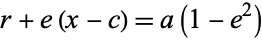
(52)

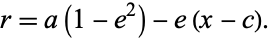
(53)

In pedal coordinates with the pedal point at the focus, the equation of the ellipse is

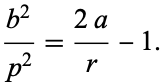
(54)

The arc length of the ellipse is

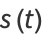
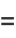
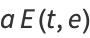
			(55)
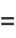
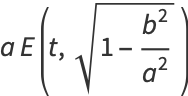
			(56)
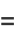
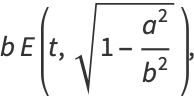
			(57)

where 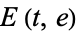is an incomplete elliptic integral of the second kind with elliptic modulus 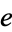(the eccentricity).

The relationship between the polar angle from the ellipse center 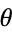and the parameter 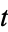follows from

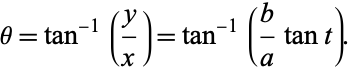
(58)

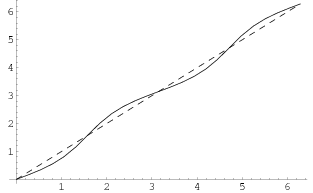
This function is illustrated above with 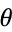shown as the solid curve and 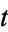as the dashed, with 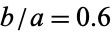. Care must be taken to make sure that the correct branch of the inverse tangent function is used. As can be seen, 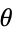weaves back and forth around 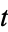, with crossings occurring at multiples of 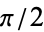. The curvature and tangential angle of the ellipse are given by

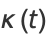
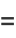
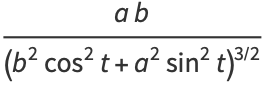
			(59)
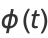
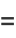
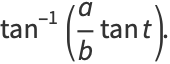
			(60)

The entire perimeter 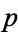of the ellipse is given by setting 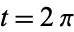(corresponding to 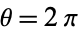), which is equivalent to four times the length of one of the ellipse's quadrants,

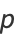
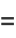
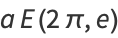
			(61)
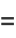
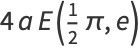
			(62)
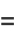
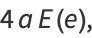
			(63)

where 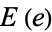is a complete elliptic integral of the second kind with elliptic modulus 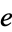(the eccentricity). The perimeter can be computed using the rapidly converging Gauss-Kummer series as

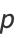
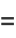
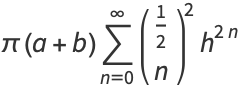
			(64)
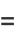
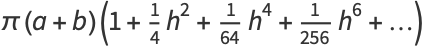
			(65)

(OEIS A056981 and A056982), where 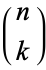is a binomial coefficient and

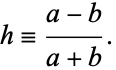
(66)

This can also be written analytically as

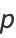
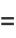
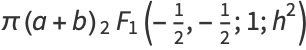
			(67)
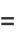
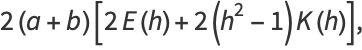
			(68)

where 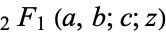is a hypergeometric function, 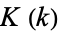is a complete elliptic integral of the first kind.

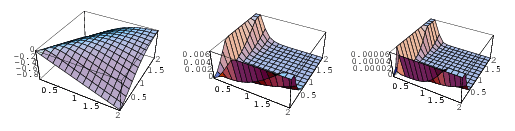
Approximations to the perimeter include

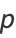
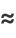
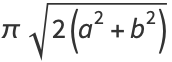
			(69)
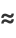
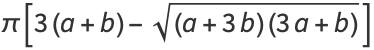
			(70)
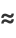
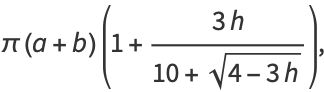
			(71)

where the last two are due to Ramanujan (1913-1914), and (71) has a relative error of 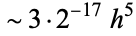for small values of 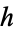. The error surfaces are illustrated above for these functions.

The maximum and minimum distances from the focus are called the apoapsis and periapsis, and are given by

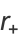
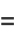
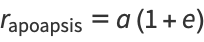
			(72)
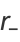
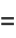
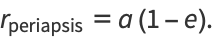
			(73)

The area of an ellipse may be found by direct integration

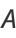
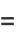
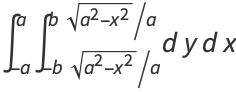
			(74)
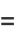
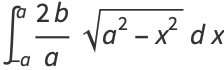
			(75)
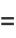
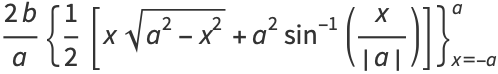
			(76)
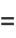
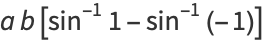
			(77)
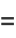
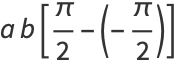
			(78)
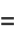
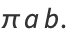
			(79)

The area can also be computed more simply by making the change of coordinates 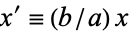and 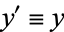from the elliptical region 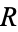to the new region 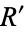. Then the equation becomes

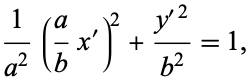
(80)

or 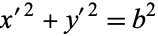, so 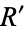is a circle of radius 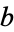. Since

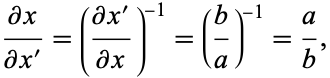
(81)

the Jacobian is

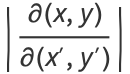
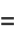
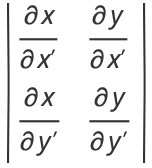
			(82)
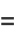
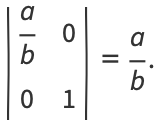
			(83)

The area is therefore

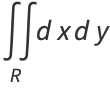
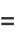
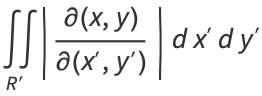
			(84)
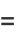
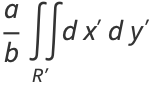
			(85)
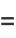
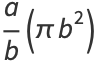
			(86)
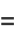
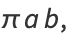
			(87)

as before. The area of an arbitrary ellipse given by the quadratic equation

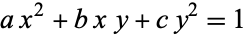
(88)

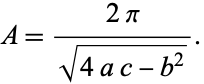
(89)

The area of an ellipse with semiaxes 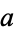and 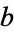with respect to a pedal point 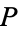is

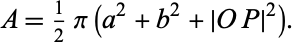
(90)

The unit tangent vector of the ellipse so parameterized is

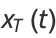
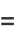
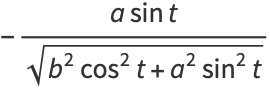
			(91)
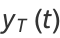
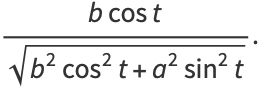
			(92)

A sequence of normal and tangent vectors are plotted above for the ellipse.

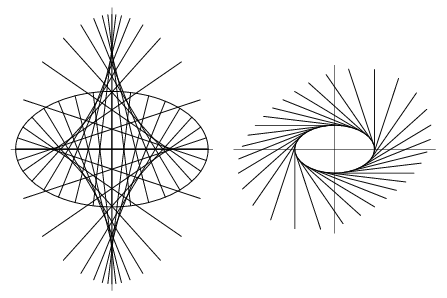
The locus of the apex of a variable cone containing an ellipse fixed in three-space is a hyperbola through the foci of the ellipse. In addition, the locus of the apex of a cone containing that hyperbola is the original ellipse. Furthermore, the eccentricities of the ellipse and hyperbola are reciprocals. The locus of centers of a Pappus chainof circles is an ellipse. Surprisingly, the locus of the end of a garage door mounted on rollers along a vertical track but extending beyond the track is a quadrant of an ellipse (Wells 1991, p. 66). (The envelope of the door's positions is an astroid.)

REFERENCES:

Abbott, P. "On the Perimeter of an Ellipse." Mathematica J. 11, 172-185, 2009.

Berger, M.; Pansu, P.; Berry, J.-P.; and Saint-Raymond, X. Problems in Geometry. New York: Springer-Verlag, 1984.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 126, 198-199, and 217, 1987.

Brown, H. T. Five Hundred and Seven Mechanical Movements. Embracing All Those Which Are Most Important in Dynamics, Hydraulics, Hydrostatics, Pneumatics, Steam Engines, Mill and Other Gearing ... and Including Many Movements Never Before Published, and Several Which Have Only Recently Come Into Use. New York: Brown, Coombs & Co., 1871.

Casey, J. "The Ellipse." Ch. 6 in A Treatise on the Analytical Geometry of the Point, Line, Circle, and Conic Sections, Containing an Account of Its Most Recent Extensions, with Numerous Examples, 2nd ed., rev. enl. Dublin: Hodges, Figgis, & Co., pp. 201-249, 1893.

Clark, W. M. and Downward, V. Mechanical Models: A Series of Working Models on the Art and Science of Mechanics. Newark, NJ: Newark Museum, 1930.

Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 75, 1996.

Coxeter, H. S. M. "Conics" §8.4 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 115-119, 1969.

Eves, H. A Survey of Geometry, rev. ed. Boston, MA: Allyn & Bacon, 1965.

Fukagawa, H. and Pedoe, D. "Ellipses," "Ellipses and One Circle," "Ellipses and Two Circles," "Ellipses and Three Circles," "Ellipses and Many Circles," "Ellipses and Triangles," "Ellipses and Quadrilaterals," "Ellipses, Circles, and Rectangles," and "Ellipses, Circles and Rhombuses." §5.1, 6.1-8.2 in Japanese Temple Geometry Problems. Winnipeg, Manitoba, Canada: Charles Babbage Research Foundation, pp. 50-68, 135-160, 1989.

Harris, J. W. and Stocker, H. "Ellipse." §3.8.7 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 93, 1998.

Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, pp. 2-3, 1999.

Kern, W. F. and Bland, J. R. Solid Mensuration with Proofs, 2nd ed. New York: Wiley, p. 4, 1948.

KMODDL: Kinetic Models for Design Digital Library. "Model: 067 Elliptical Gears." http://kmoddl.library.cornell.edu/model.php?m=557.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 72-78, 1972.

Lockwood, E. H. "The Ellipse." Ch. 2 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 13-24, 1967.

MacTutor History of Mathematics Archive. "Ellipse." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Ellipse.html.

Ramanujan, S. "Modular Equations and Approximations to 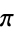." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.

Reuleaux, F. and Kennedy, A. B. W. (Eds.). Kinematics of Machinery: Outlines of a Theory of Machines. London: Macmillan, 1876. Reprinted by New York: Dover, 1976.

Sloane, N. J. A. Sequences A056981 and A056982 in "The On-Line Encyclopedia of Integer Sequences."

Trott, M. The Mathematica GuideBook for Symbolics. New York: Springer-Verlag, 2006. http://www.mathematicaguidebooks.org/.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 63-67, 1991.

Yates, R. C. "Conics." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 36-56, 1952.

CITE THIS AS:

Weisstein, Eric W. "Ellipse." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Ellipse.html

Ellipse（椭圆）相关推荐

iOS 2D绘图详解（Quartz 2D）之路径(点,直线,虚线,曲线,圆弧,椭圆,矩形)
前言:一个路径可以包含由一个或者多个shape以及子路径subpath,quartz提供了很多方便的shape可以直接调用.例如:point,line,Arc(圆弧),Curves(曲线),Ellip ...
椭圆 / 椭圆的画法
原文链接: https://www.lfhacks.com/t/draw-ellipse 在现实生活中如何画椭圆 ?椭圆并不是由圆压扁而来,而是要符合一定的规则才能称为椭圆.现实生活中如果有画椭圆的 ...
css 形状_在CSS形状之外思考
css 形状 CSS is based off a box model. If you have an image that is a circle that you want to wrap tex ...
R语言绘图：28个实用程序包
本文转载自" 阿虎定量笔记",作者郑连虎,转载己获授权.其他人转载请联系原作者,点我跳转原文. 全文注释 # 示例参考帮助文档 # 我用Rstudio重现了所有示例 # 初识R语言 ...
LISP 图层前后缀_lisp获取qleader端点_lisp以一个图层来做定义快名称怎么实现
★快捷命令的命名规律 1. 快捷命令通常是该命令英文单词的第一个或前面两个字母,有的是前三个字母. 比如,直线(Line)的快捷命令是"L":复制(COpy)的快捷命令是" ...
butter滤波器是iir吗_如何快速设计一个IIR滤波器
在文章如何快速设计一个FIR滤波器(一)以及如何快速设计一个FIR滤波器(二)等文章中,我们讨论了如何设计FIR(Finite Impulse Response Filter),FIR有很多优点,比如 ...
db2top详细使用方法_Py之PIL：Python的PIL库的简介、安装、使用方法详细攻略
Py之PIL:Python的PIL库的简介.安装.使用方法详细攻略目录 PIL库的简介 PIL库的安装 PIL库的用方法 1.几何图形的绘制与文字的绘制 2.绘制图形的各种案例 PIL库的简介 PI ...
收藏 | 28个R语言绘图的实用程序包！
作者:郑连虎来源:阿虎定量笔记本文约2500字,建议阅读20+分钟. 本文为大家介绍了关于R语言绘图方面28个实用程序包. cartogram 扭曲的地图,以传达统计信息开发 Sebastian ...
Direct2D教程（三）简单几何图形
从本章开始,我们介绍D2D几何图形. D2D图形分类 Direct2D支持多种类型的几何图形,包括 Simple Geometry(简单几何图形) 矩形圆角矩形椭圆 Path Geometry(路 ...
cad 快捷键命令大全
目录符号键(CTRL开头) 控制键组合键功能键换挡键首字母前两个字母两个字母(间隔) 三个字母(间隔) JOG 无规律的个别符号键(CTRL开头) CTRL+1 PROPCLOSEOR ...

Ellipse（椭圆）

Ellipse（椭圆）相关推荐

最新文章

热门文章