凸函数、凸规划的定义及学习

1、计算几何是研究什么的？

计算几何研究的对象是几何图形。早期人们对于图像的研究一般都是先建立坐标系，把图形转换成函数，然后用插值和逼近的数学方法，特别是用样条函数作为工具来分析图形，取得了可喜的成功。然而，这些方法过多地依赖于坐标系的选取，缺乏几何不变性，特别是用来解决某些大挠度曲线及曲线的奇异点等问题时，有一定的局限性。

2、计算几何理论中过两点的一条直线的表达式，是如何描述的？
通过以下公式模型进行对平面几何形象化的描述：
我们假设有两个点:A(x1,y1)、B(x2,y2)
那么这两个点确定的直线方程我们假设如下:
Ax+By+C=0
那么其中A为:y2−y1
其中B为:x2−x1
最后可得出常数c的结果:C=−Ax1−By1=x2y1−x1y2
python代码如下：

def LineMake(X,Y):a = B[1]-A[1]b = A[0]-B[0]c = B[0] * A[1] - A[0] * B[1]l="确定的直线方程为："+str(a)+"x+"+str(b)+"y+"+str(c)+"=0"return l
}

3.1、凸集是什么？
在凸几何中，凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说，在欧氏空间中，凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。例如，立方体是凸集，但是任何中空的或具有凹痕的例如月牙形都不是凸集。
特别的，凸集，实数R上（或复数C上）的向量空间中，如果集合S中任两点的连线上的点都在S内，则称集合S为凸集。
3.2、直线是凸集吗？

凸集是单点或一条不间断的线（包括直线、射线、线段）；二、三维空间中的凸集就是直观上凸的图形。（例如：在二维中有扇面、圆、椭圆等，在三维中有实心球体等；多数情况下，两个凸集的交集也是凸集，空集也是凸集）
**3.3、直线是仿射集吗？**
非空间射集M的维数定义为，上述子空间L的维数。空集的维数定义为-1。维数分别为0、1,以及2的仿射集为点、直线和平
面。R"中n-.维点仿射集称为超平面。
**4、三维空间中的一个平面，如何表达**
三维空间中的平面主要通过建立公式模型来解答，例如
我们假设三维的直线方程为:Ax+By+Cz+D=0显而易见，我们需要的求解的便是其中的A、B、C、D的未知参量
那么我们如何求解其中的未知参量呢？便要通过特定的求解方法啦！
求解未知参量A、B、C、D的方法：最原始的解法是根据已知的三个点，建立3个联合方程组,来消元高斯消元法克莱姆法则(适用于变量和方程数目相等)
**5、更高维度的“超平面”，如何表达？**
1、什么是超平面？
超平面的数学定义是这样的：超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。因为是子空间，所以超平面一定过原点。
2、高维度超平面的表达
在数学中，超平面（Hyperplane）是n维欧氏空间中余维度等于1的线性子空间。这是平面中的直线、空间中的平面之推广。设F为域其中
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200422163711893.png)超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。设d是n维欧式空间R中的一个非零向量，a是实数，则R中满足条件dX=a的点X所组成的集合称为R中的一张超平面。
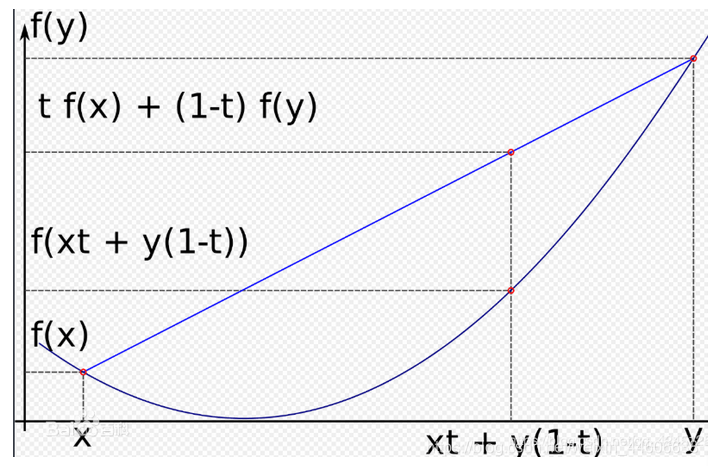
**6.1、什么是“凸函数”定义？**
任意两点的函数值的连线上的点都在曲线的上方，我们成为凸函数。数学模型如下：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200422163850410.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NDYwNjYzOA==,size_16,color_FFFFFF,t_70)
**6.2、什么是Hessen矩阵？**
Hessian Matrix（黑塞矩阵、海森矩阵、海瑟矩阵、海塞矩阵 etc.）,它是一个多元函数的二阶偏导数构成的方阵，用以描述函数的局部曲率。黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出，并以其名字命名。黑塞矩阵常用于牛顿法解决优化问题。
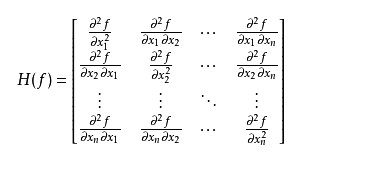
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200422163938712.png)
**6.3、 如何判别一个函数是凸函数？**
1、一元函数的判别
对于一元函数f(x)f(x)，我们可以通过其二阶导数f′′(x)f″(x) 的符号来判断。如果函数的二阶导数总是非负，即f′′(x)≥0f″(x)≥0 ，则f(x)f(x)是凸函数
2、多元函数的判别
对于多元函数f(X)f(X)，我们可以通过其Hessian矩阵（Hessian矩阵是由多元函数的二阶导数组成的方阵）的正定性来判断。如果Hessian矩阵是半正定矩阵，则是f(X)f(X)凸函数**6.4、f(x)=x^3 函数是凸函数吗？**
该数学模型图的python代码如下所示：
```python
import matplotlib.pyplot as plt
import numpy as np
x=np.array([])
y=np.array([])
for i in range(-50,51,1):x=np.insert(x,len(x),i)y=np.insert(y,len(y),x[len(y)]**3)
h=1000*x
plt.plot(x,y)
plt.plot(x,h)
plt.grid()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('f(x)-y')
plt.show()

由图可以看出来直线y=1000x去截去该函数时，直线上的所有点，不都在曲线的上方，因此，该公式模型不是凸函数。
7.1、什么是“凸规划”？
凸规划的数学定义如下所示：
7.2、如何判别一个规划问题是凸规划问题
凸规划有三点附加条件：
（1）目标函数f(x)f(x)必须是凸函数；
（2）不等式约束函数gi(x)gi(x)必须是凸函数，不等式gi(x)≤0gi(x)≤0组成的区域为凸集；
（3）等式约束函数hj(x)=aTjx−bjhj(x)=ajTx−bj必须是仿射的（即线性函数和常函数的和函数）。
因此我们得出以下结论：凸规划的可行域是凸集。因为每个约束条件的点集都是凸集，它们的交集也是凸集。
7.3、验证下图例题是凸规划
例题：
判断该例题的python代码如下:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
x1=np.array([])
x2=np.array([])
x3=np.array([])
for i in range(-100,100,1):x1=np.insert(x1,len(x1),i)x2=np.insert(x2,len(x2),i)x3=np.insert(x3,len(x3),i)
h=2*x1**2+x2**2+2*x3**2+x1*x3-x1*x2+x1+2*x2
h1=x1**2+x2**2-x3
h2=x1+x2+x3*2-16
h3=-x1-x1+x3
ax=plt.figure().add_subplot(111,projection='3d')
ax.scatter(x1,x2,h,c='r',marker='o')
ax.plot(x1,x2,h1)
ax.plot(x1,x2,h2)
ax.plot(x1,x2,h3)
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel("fx")
plt.show()

结果显示：
由此可以直接看出该方程为凸规划。

凸函数、凸规划的定义及学习相关推荐

关于函数式宏定义的学习
题记:回头看看原本学过的知识,发现那些原本以为理解了的皮毛都突然让自己变得陌生.逐步学习,不懈努力. 测试题目时发现得出的结论与自己给出的不同,于是查阅资料,重新学习宏定义相关的文章.在C与C++编程 ...
python变量如何用循环定义_Python学习日记1（变量定义，分支，循环）
学习历程按照Github上jackfrued的100天学习python的进度来进行,再辅上一些自己查找的相关资料. 对应传送门:https://github.com/jackfrued/Python- ...
自己定义View学习之12/7(进度条之混合模式)
今天重点内容是我们学习自己定义view里面的混合模式.事实上我们的画布就跟photoshop一样.是个图层关系,一层盖着一层.这样就导致有非常多种覆盖模式,这就是我们今天的主题."混合模式& ...
html 超链接 javascript 函数 java 未定义_JavaScript 学习笔记（一）
本系列适合作为JS的复习文档. 学习JavaScript,不要以为会做一两个如图片切换.tabs选项卡这样特效,就是精通JavaScript了.JavaScript不仅仅是用来做一两个特效,它更大的用 ...
shell中文件路径用变量定义_shell学习笔记01（概述amp;变量）
Shell概述为什么要学习Shell呢? 因为有用. Shell脚本入门 1．脚本格式脚本以#!/bin/bash开头(指定解析器) 2．第一个Shell脚本:helloworld (1)需求:创 ...
oracle 隐藏视图定义,【学习笔记】show hidden parameter 创建查看隐藏参数视图
天萃荷净分享一篇开发DBA常用的show hidden parameter,创建查看隐藏参数视图的案例步骤 1.创建查看隐藏参数视图(show_hidden_v$parameter) --conn ...
mysql 浮点数定义2_MySQL学习笔记（二）：数据类型
MySQL的数据类型还是较为简单的,总共有四种:整数类型.浮点数类型.字符串类型.时间和日期类型. 整数类型从小到大有tinyint.smallint.mediumint.int.bigint五种,区 ...
七、MySQL DDL数据定义语言学习笔记（库和表的创建、修改、删除详解 + 强化复习）
DDL语言数据定义语言库和表的管理: 一.库的管理: 创建.修改.删除二.表的管理: 创建.修改.删除创建: create 修改: alter 删除: drop 一.库的管理 1.库的创建: ...
python 单一继承定义_Python学习之单继承与多继承
继承面向对象编程语言的一个主要功能就是"继承". 继承是指这样一种能力:它可以使用现有类的所有功能,并在无需重新编写原来的类的情况下对这些功能进行扩展. (1)单继承:pytho ...

凸函数、凸规划的定义及学习

凸函数、凸规划的定义及学习相关推荐

最新文章

热门文章