链接：http://blog.csdn.net/zwlforever/archive/2008/03/14/2183049.aspx
一篇不错的FFT 文章，收藏一下。
DFT的的正变换和反变换分别为（1）和（2）式。假设有N个数据，则计算一个频率点需要N次复数乘法和N-1次复数加法，整个DFT需要N*N次复数乘法和N（N-1）次复数加法；由于一次的复数乘法需要进行4次的实数乘法和2次的复数加法，一次的复数加法需要两次的实数加法，因此整个DFT需要4*N*N次的实数乘法和2*N（N-1）+2*N*N≈4*N*N次的复数加法。当N比较大时，所需的计算工作量相当大，例如N=1024时大约需要400万次乘法运算，对于实时信号处理来说，将对计算设备提出非常苛刻的要求，于是就提出如何能够减少计算DFT的运算量的问题。

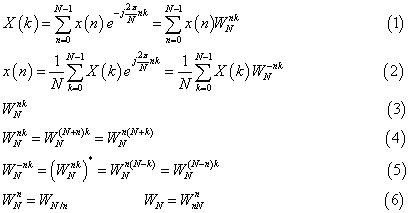
1965年，库力和图基在《计算数学》杂志上发表《机器计算傅立叶级数的一种算法》，此文是最早提出FFT算法的。此后关于DFT的快速算法称为人们研究的热点课题，也正是FFT算法的出现，才使得数字信号处理能够应用于实时场合并进一步推动数字信号处理的发展和应用。

大多数的FFT算法都是利用（3）式的周期性、共轭对称性、可压缩和扩展性的特点来压缩计算量。。

1）、根据DFT定义进行计算的代码

//Data为输入数据指针，Log2N=log2(length),flag=-1时为正变换，flag=1时为反变换，变换结果同样由指针Data指向的空间返回
void dft(complex<double>*Data,int Log2N,int flag)

{

int i,j,length;

complex<double> wn;

length=1<<Log2N;

complex<double>*temp=new complex<double>(length);

for(i=0;i<length;i++)

{

temp[i]=0;

for(j=0;j<length;j++)

{

wn=complex<double>(cos(2.0*pi/length*i*j),sin(flag*2.0*pi/length*i*j));

temp[i]+=Data[j]*wn;

}

if(flag==1)

for(i=0;i<length;i++)

Data[i]=temp[i]/length;

delete[] temp;

}

2）、基2时间抽选FFT

把时域的数字信号序列按照奇偶进行分组计算，可以进行如下的变换，从变换结果可以知道，一个长度为N的DFT可以变换成长度为N/2的两个子序列的组合。依次类推，可以直到转为N/2个2点的傅立叶变化的组合。不过这时的输入应该为以2为基的倒位序。

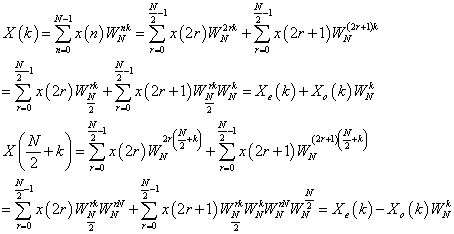
由于经过多次的奇偶抽选，输入数据要按照基2倒序的原则进行重排，输出数据为正常顺序，倒序算法另外叙述。下面首先用递归的形式进行算法的描述，由于递归方法没有充分利用DIT2算法的优点---原位计算，因此递归形式只是为了描述的清晰。

void dit2rec(complex<double>*InData,complex<double>*OutData,int length,int sign)

{

complex<double>*EvenData=new complex<double>(length/2);

complex<double>*OddData =new complex<double>(length/2);

complex<double>*EvenResult=new complex<double>(length/2);

complex<double>*OddResult=new complex<double>(length/2);

int i,j;

if(length==1)

{

OutData[0]=InData[0]/N;

return;

}

for(i=0;i<length/2;i++)

{

EvenData[i]=InData[2*i];

OddData[i]=InData[2*i+1];

}

dit2rec(EvenData,EvenResult,length/2,sign);

dit2rec(OddData,EvenResult,length/2,sign);

for(i=0;i<length/2;i++)

{

OutData[i]=EvenData+OddData*complex<double>(cos(2*pi*i/length),sin(sign*2*pi*i/length));

OutData[i+length/2]=EvenData- OddData*complex<double>(cos(2*pi*i/length),sin(sign*2*pi*i/length));

}

delete[] EvenData,OddData,EvenResult,OddResult;

return;

}

非递归实现如下（现不考虑输入的倒序数问题）：

void dit2(complex<double>*Data,int Log2N,int sign)

{

int i,j,k,step,length;

complex<double> wn,temp,deltawn;

length=1<<Log2N;

for(i=1;i<=Log2N;i++)

{

wn=1;step=1<<i;deltawn=complex<double>(cos(2*pi/step),sin(sign*2.0*pi/step))；

for(j=0;j<step/2;j++)

{

for(i=0;i<length/step;i++)

{

temp=Data[i*step+step/2+j]*wn;

Data[i*step+step/2+j]=Data[i*step+j]-temp;

Data[i*step+j]=Data[i*step+j]+temp;

}

wn=wn*deltawn;

}

if(sign==-1)

for(i=0;i<length;i++)

Data[i]/=length;

}

当i=1时，也就是第一次循环并没有必要进行复数运算，因为j只能取1，wn为实数，这个时间可以节省。因此可以改进为:

void dit2(complex<double>*Data,int Log2N,int sign)

{

int i,j,k,step,length;

complex<double> wn,temp,deltawn;

length=1<<Log2N;

for(i=0;i<length;i+=2)

{

temp=Data[i];

Data[i]=Data[i]+Data[i+1];

Data[i+1]=temp-Data[i+1];

}

for(i=2;i<=Log2N;i++)

{

wn=1;step=1<<i;deltawn=complex<double>(cos(2.0*pi/step),sin(sign*2.0*pi/step));；

for(j=0;j<step/2;j++)

{

for(i=0;i<length/step;i++)

{

temp=Data[i*step+step/2+j]*wn;

Data[i*step+step/2+j]=Data[i*step+j]-temp;

Data[i*step+j]=Data[i*step+j]+temp;

}

wn=wn*deltawn;

}

if(sign==1)

for(i=0;i<length;i++)

Data[i]/=length;

}

3）、基2频率抽选FFT

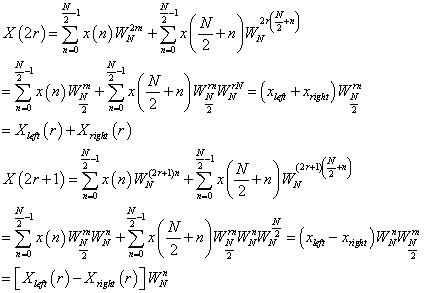
//DIF2的递归版本实现：

void dif2rec(complex<double>*InData,complex<double>*OutData,int length,int sign)

{

complex<double>* LData=new complex<double>(length/2);

complex<double>* LResult=new complex<double>(length/2);

complex<double>* RData=new complex<double>(length/2);

complex<double>* RResult=new complex<double>(length/2);

complex<double> temp;

int i;

if(length==1)

{

OutData[0]=InData[0];

return;

}

for(i=0;i<length/2;i++)

{

LData[i]=InData[i];

RData[i]=InData[i+length/2];

}

for(i=0;i<length/2;i++)

{

temp=LData[i];

LData[i]=LData[i]+RData[i];

RData[i]=(temp-RData[i])* complex<double>(cos(2*pi*i/length),sin(sign*2*pi*i/length))

}

dit2rec(LData,LResult,length/2,sign);

dit2rec(RData,RResult,length/2,sign);

for(i=0;i<length/2;i++)

{

OutData[2*i]=LResult[i];

OutData[2*i+1]=RResult[i];

}

return;

}

//非递归实现如下（现不考虑输入的倒序数问题）：

void dif2(complex<double>*InData,int r,int sign)

{

int length=1<<r;

int i,j,k,step;

complex<double> temp,wn;

for(i=1;i<=r;i++)

{

step=1<<(r-i+1);

wn=1;

for(j=0;j<step/2;j++)

{

for(k=0;k<step/2;k++)

{

temp=InData[k*step+j];

InData[k*step+j]=InData[k*step+j]-InData[k*step+step/2+j];

InData[k*step+step/2+j]=(temp-InData[k*step+step/2+j])*wn;

}

wn=wn*complex<double>(cos(2*pi/step*j),sin(sign*2*pi/step*j));

}

和DIT一样，最外层的最后一个循环可以另外独立出来，因为最后一个循环没有必要进行复数运算，这样可以减少复数运算的次数。

基四时间抽选快速傅立叶算法

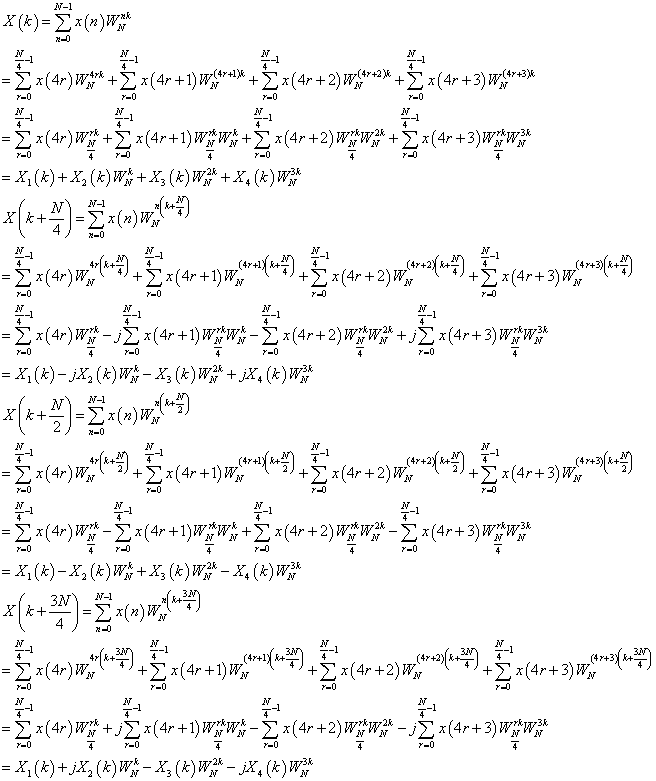
转载于:https://www.cnblogs.com/Free-Thinker/p/4759955.html

几种快速傅里叶变换(FFT)的C++实现相关推荐

基于python的快速傅里叶变换FFT（二）
基于python的快速傅里叶变换FFT(二) 本文在上一篇博客的基础上进一步探究正弦函数及其FFT变换. 知识点 FFT变换,其实就是快速离散傅里叶变换,傅立叶变换是数字信号处理领域一种很重要的算 ...
Java中实现快速傅里叶变换FFT
Java中实现快速傅里叶变换FFT 一.概述 1.傅里叶变换(FT) 2.离散傅里叶变换(DFT) 3.快速傅里叶变换(FFT) 1)单位根 2)快速傅里叶变换的思想 3)蝶形图 4)快速傅里叶变换的 ...
OpenCV快速傅里叶变换(FFT)用于图像和视讯流的模糊检测
OpenCV快速傅里叶变换(FFT)用于图像和视频流的模糊检测翻译自[OpenCV Fast Fourier Transform (FFT) for blur detection in images ...
Matlab如何进行利用离散傅里叶变换DFT (快速傅里叶变换FFT)进行频谱分析
文章目录 1. 定义 2. 变换和处理 3. 函数 4. 实例演示例1:单频正弦信号(整数周期采样) 例2:单频正弦信号(非整数周期采样) 例3:含有直流分量的单频正弦信号例4:正弦复合信号例5 ...
Java编程实现快速傅里叶变换FFT
快速傅里叶变换的时间复杂度分析 1 快速傅里叶变换FFT 1.1 理论分析 1.1.1 离散傅里叶变换 1.1.2 快速傅里叶变换 1.2 编程实现 1.2.1 算法思想 1.2.2 实验结果 1 快 ...
快速傅里叶变换python_基于python的快速傅里叶变换FFT（二）
基于python的快速傅里叶变换FFT(二) 本文在上一篇博客的基础上进一步探究正弦函数及其FFT变换. 知识点 FFT变换,其实就是快速离散傅里叶变换,傅立叶变换是数字信号处理领域一种很重要的算法. ...
离散傅里叶变换 (DFT)、快速傅里叶变换 (FFT)
目录离散傅里叶变换 (DFT) 离散傅里叶变换的基离散傅里叶变换快速傅里叶变换 (FFT) 卷积线性时不变系统傅里叶级数参考文献离散傅里叶变换 (DFT) 离散傅里叶变换的基对于周期为 ...
matlab cftool光滑曲线导出为什么就不光滑了_快速傅里叶变换(FFT)中为什么要“补零”？...
为了大家能够复现各个图中的结果,我附上了所有我编写的MATLAB代码. 创作不易,未经允许,禁止转载. 另外,说明一下,用MATLAB做FFT并不要求数据点个数必须为以2为基数的整数次方.之所以很多资 ...
[模板] 快速傅里叶变换(FFT)
快速傅里叶变换FFT 多项式转换快速傅里叶变换铺垫定理算法构建 IFFT 递归版FFT&IFFT 迭代版FFT&IFFT 蝴蝶效应 Code 后记多项式假设有nnn次多项 ...

几种快速傅里叶变换(FFT)的C++实现

2）、基2时间抽选FFT

几种快速傅里叶变换(FFT)的C++实现相关推荐

最新文章

热门文章