四边形不等式优化动态规划原理:

1.当决策代价函数w[i][j]满足w[i][j]+w[i’][j’]<=w[I;][j]+w[i][j’](i<=i’<=j<=j’)时,称w满足四边形不等式.当函数w[i][j]满足w[i’][j]<=w[i][j’] i<=i’<=j<=j’)时,称w关于区间包含关系单调.

2.如果状态转移方程m为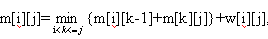且决策代价w满足四边形不等式的单调函数(可以推导出m亦为满足四边形不等式的单调函数),则可利用四边形不等式推出最优决策s的单调函数性,从而减少每个状态的状态数,将算法的时间复杂度由原来的O(n^3)降低为O(n^2).方法是通过记录子区间的最优决策来减少当前的决策量.令:

s[i][j]=max{k | ma[i][j] = m[i][k-1] + m[k][j] + w[i][j]}

由于决策s具有单调性,因此状态转移方程可修改为:

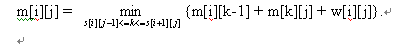
证明过程: (转载)

设m[i,j]表示动态规划的状态量。

m[i,j]有类似如下的状态转移方程：

m[i,j]=opt{m[i,k]+m[k,j]}(i≤k≤j)

如果对于任意的a≤b≤c≤d，有m[a,c]+m[b,d]≤m[a,d]+m[b,c]，那么m[i,j]满足四边形不等式。

以上是适用这种优化方法的必要条件

对于一道具体的题目，我们首先要证明它满足这个条件，一般来说用数学归纳法证明，根据题目的不同而不同。

通常的动态规划的复杂度是O(n³)，我们可以优化到O(n²)

设s[i,j]为m[i,j]的决策量，即m[i,j]=m[i,s[i,j]]+m[s[i,j]+j]

我们可以证明，s[i,j-1]≤s[i,j]≤s[i+1,j]  （证明过程见下）

那么改变状态转移方程为：

m[i,j]=opt{m[i,k]+m[k,j]}      (s[i,j-1]≤k≤s[i+1,j])

复杂度分析：不难看出，复杂度决定于s的值，以求m[i,i+L]为例，

(s[2,L+1]-s[1,L])+(s[3,L+2]-s[2,L+1])…+(s[n-L+1,n]-s[n-L,n-1])=s[n-L+1,n]-s[1,L]≤n

所以总复杂度是O(n²)

对s[i,j-1]≤s[i,j]≤s[i+1,j]的证明：

设m_k[i,j]=m[i,k]+m[k,j]，s[i,j]=d

对于任意k<d，有m_k[i,j]≥m_d[i,j]（这里以m[i,j]=min{m[i,k]+m[k,j]}为例,max的类似），接下来只要证明m_k[i+1,j]≥m_d[i+1,j]，那么只有当s[i+1,j]≥s[i,j]时才有可能有m_s[i+1,j][i+1,j]≤m_d[i+1,j]

(m_k[i+1,j]-m_d[i+1,j]) - (m_k[i,j]-m_d[i,j])

=(m_k[i+1,j]+m_d[i,j]) - (m_d[i+1,j]+m_k[i,j])

=(m[i+1,k]+m[k,j]+m[i,d]+m[d,j]) - (m[i+1,d]+m[d,j]+m[i,k]+m[k,j])

=(m[i+1,k]+m[i,d]) - (m[i+1,d]+m[i,k])

∵m满足四边形不等式，∴对于i<i+1≤k<d有m[i+1,k]+m[i,d]≥m[i+1,d]+m[i,k]

∴(m_k[i+1,j]-m_d[i+1,j])≥(m_k[i,j]-m_d[i,j])≥0

∴s[i,j]≤s[i+1,j]，同理可证s[i,j-1]≤s[i,j]

证毕

扩展：

以上所给出的状态转移方程只是一种比较一般的，其实，很多状态转移方程都满足四边形不等式优化的条件。

解决这类问题的大概步骤是：

0.证明w满足四边形不等式，这里w是m的附属量，形如m[i,j]=opt{m[i,k]+m[k,j]+w[i,j]}，此时大多要先证明w满足条件才能进一步证明m满足条件

1.证明m满足四边形不等式

2.证明s[i,j-1]≤s[i,j]≤s[i+1,j]

pku 1160 Post Office 解题报告

题意: 给出m个村庄及其距离，给出n个邮局，要求怎么建n个邮局使代价最小.

算法:很显然用到动态规划,那么假设:

d[i…n],各邮局的坐标

w[i][j]表示在d[i][j]之间建立一个邮局的村庄为k,则k为i与j之和的一半(很显然在中间建一个邮局距离最小),那么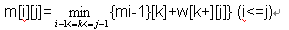

m[i][j]为在前j个村庄建立i个邮局的最小距离和.

那么状态转移方程为:

边界条件: m[1][j]=w[1][j]  (1<=j<=m)

状态转移方程: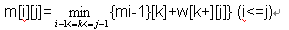 

那么思路则为:

for i=2 to p do      //递推邮局数

{

//m:在前j个村庄建立i个邮局的最小距离和

for j=n dwonto i+1 do    //按递减顺序枚举尾指针

m[i][j]=inf;

for k=1 to n do

{

temp = m[i-1][k]+calcw(k+1,j);

if(temp<m[i][j]) m[i][j]=temp;

}

}

这样时间复杂度显然为O(n^3),这是不能接受的.

仔细分析这dp算法,关键是决策变量k枚举数太多, 联系到四边形不等式原理,w[i][j]与m[i][j]很明显符合四边形不等式,我们假设决策变量s[i][j],如果在1到10的村庄中,建立1个邮局的最佳位置为8,那么在决定见多一个邮局的话,当然是在1到8之间了(根据四边形不等式原理猜想到),所以就在dp的过程中,用s[i][j]记录前i-1个邮局的村庄数. 那么我们第三次搜索的时候,就需要根据决策表s[i-1][j]<=k<=s[i][j+1]的范围内枚举.而可以证明s[i][j]具有单调性,那么我们就可以利用s[i][j]单调性限制了上下界然后把 O(n^3)弄成了 O(n^2)。

以sample为例:

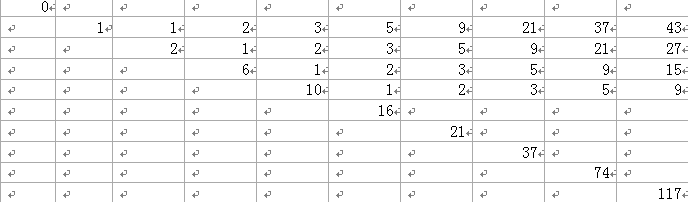
状态方程m:

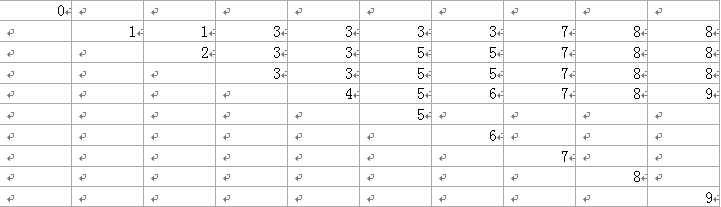
决策表s:

那么状态转移方程为:

边界条件: m[1][j]=w[1][j]  (1<=j<=m)

边界条件: m[1][j]=w[1][j]  (1<=j<=m)

状态转移方程: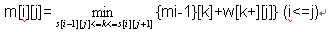 

决策记录表: s[i][j]=k

代码:

View Code

//#pragma comment(linker,"/STACK:327680000,327680000")
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#include <algorithm>
#include <string>
#include <set>
#include <functional>
#include <numeric>
#include <sstream>
#include <stack>
#include <map>
#include <queue>#define CL(arr, val)    memset(arr, val, sizeof(arr))
#define REP(i, n)       for((i) = 0; (i) < (n); ++(i))
#define FOR(i, l, h)    for((i) = (l); (i) <= (h); ++(i))
#define FORD(i, h, l)   for((i) = (h); (i) >= (l); --(i))
#define L(x)    (x) << 1
#define R(x)    (x) << 1 | 1
#define MID(l, r)   (l + r) >> 1
#define Min(x, y)   (x) < (y) ? (x) : (y)
#define Max(x, y)   (x) < (y) ? (y) : (x)
#define E(x)        (1 << (x))
#define iabs(x)     (x) < 0 ? -(x) : (x)
#define OUT(x)  printf("%I64d\n", x)
#define Read()  freopen("data.in", "r", stdin)
#define Write() freopen("data.out", "w", stdout);typedef long long LL;
const double eps = 1e-8;
const double PI = acos(-1.0);
const int inf = ~0u>>2;using namespace std;const int N = 310;
const int M = 33;int dp[N][N];
int s[N][N];
int d[N];
int sum[N][N];int dis(int i, int j) {if(i >= j)  return 0;if(sum[i][j] != 0)  return sum[i][j];int a = i, b = j;while(a < b) {sum[i][j] += (d[b--] - d[a++]);}return sum[i][j];
}int main() {//Read();int i, j, k, V, P, tmp;while(~scanf("%d%d", &V, &P)) {for(i = 1; i <= V; ++i) {scanf("%d", d + i);}CL(sum, 0);CL(dp, 0);for(i = 1;  i <= V; ++i) {dp[1][i] = dis(1, i);s[i][i] = i-1;}for(i = 2; i <= P; ++i) {s[i][V+1] = V-1;for(j = V; j >= i; --j) {dp[i][j] = inf;for(k = s[i-1][j]; k <= s[i][j+1]; ++k) {tmp = dp[i-1][k] + dis(k + 1, j);if(tmp < dp[i][j]) {dp[i][j] = tmp;s[i][j] = k;}}}}printf("%d\n", dp[P][V]);}return 0;
}