数学-泰勒展开和拉格朗日

欧拉公式

$e^{ix}=\cos x+i\sin x$
基础思想：不断运动中藏着完美的果实。
通俗描述：泰勒展开映射到多维空间的宏？
$e^{i\pi}=\cos\pi+isin\pi=-1\Rightarrow e^{i\pi}+1=0$

泰勒展开

基础思想：无限的努力可以逼近成功。
通俗描述：仿造一条曲线，首先仿造它的初始点，然后是它的斜率，然后是它的二阶斜率。。不断递进。
数学定理:
链接：https://www.zhihu.com/question/25627482/answer/313088784
来源：知乎

先算个一阶的。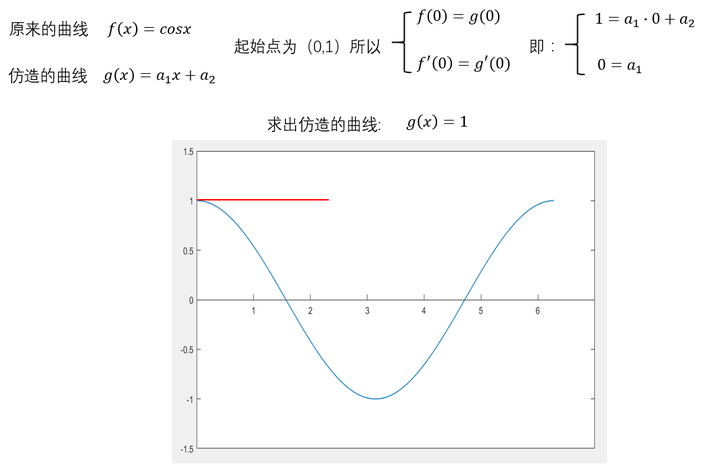可以看出，除了在这个点，其他的都不重合，不满意。再来个二阶的。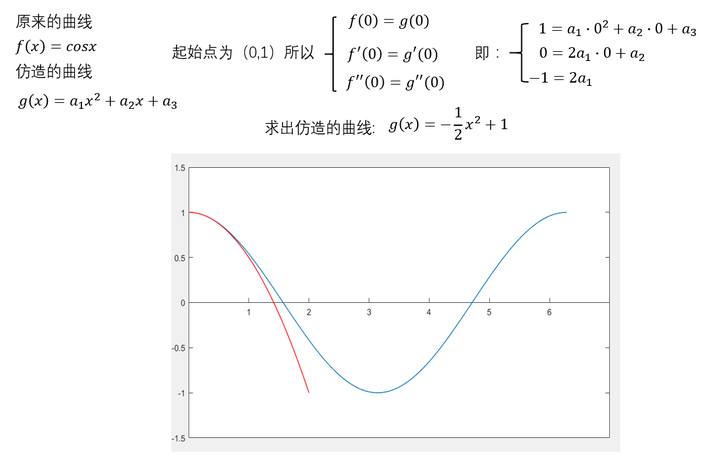可以看出，在这个点附近的一个小范围内，二者都比较相近。再来个四阶的。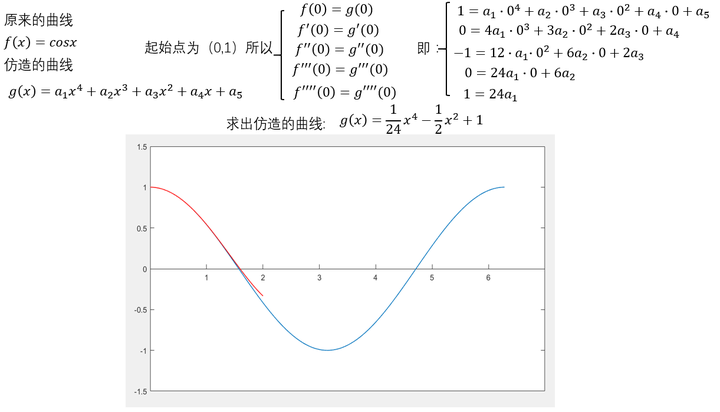可以看出，仍然是在这个点附近的一个范围内二者很相近。只是，此时二者重合的部分扩大了。到这里，不光是泰勒，我们普通人也能大概想象得到，如果继续继续提高阶数，相似范围继续扩大，无穷高阶后，整个曲线都无限相似。插个图，利用计算机可以快速实现。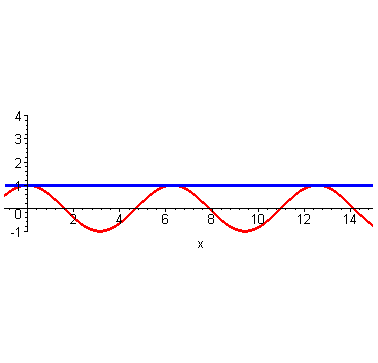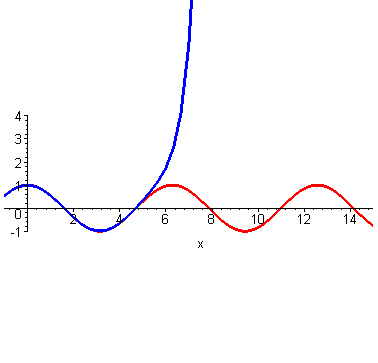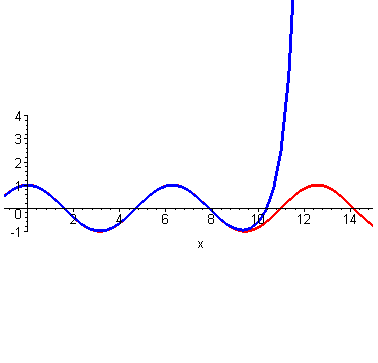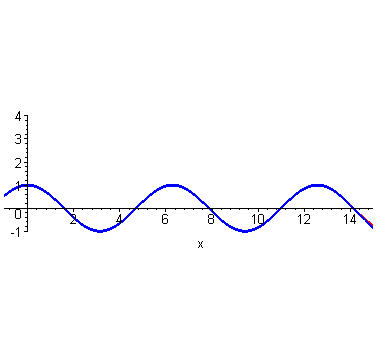

有一条解析式很复杂的曲线，我可以用多项式仿造一条曲线, 那么
f(x)≈g(x)=g(x0)+f1(x0)1！(x−x0)+f2(x0)2！(x−x0)2+......+fn(x0)n！(x−x0)nf(x) \approx g(x) =g(x_0)+\frac{f^1(x_0)}{1！}(x-x_0)+\frac{f^2(x_0)}{2！}(x-x_0)^2+......+\frac{f^n(x_0)}{n！}(x-x_0)^nf(x)≈g(x)=g(x0)+1！f1(x0)(x−x0)+2！f2(x0)(x−x0)2+......+n！fn(x0)(x−x0)n
泰勒指出：在实际操作过程中，可根据精度要求选择n值，只要n不是正无穷，那么，一定要保留上式中的约等号。若想去掉约等号，可写成下面形式：
f(x)=g(x)=g(x0)+f1(x0)1！(x−x0)+f2(x0)2！(x−x0)2+......f(x) = g(x) =g(x_0)+\frac{f^1(x_0)}{1！}(x-x_0)+\frac{f^2(x_0)}{2！}(x-x_0)^2+......f(x)=g(x)=g(x0)+1！f1(x0)(x−x0)+2！f2(x0)(x−x0)2+......

佩亚诺然后将误差的值通过泰勒展开中最小的一项进行限定。并求坐商。
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210301104318490.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L20wXzM4MDI0MDk3,size_16,color_FFFFFF,t_70

拉格朗日

基础思想：只要事物曾经运动过，这其中必然有一个可以衡量它运动状态的已知量。->只要问题存在解决方案，则必然在其中存在一个合理评价标准下的最优解。
同等量级的无穷小可以相互替换以尝试简化结果。
通俗描述：
平均速度存在于斜率之中

数学定理:
作者：「已注销」
链接：https://www.zhihu.com/question/25627482/answer/313088784
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

首先，跟佩亚诺一样，先把误差项写出来，并设误差项为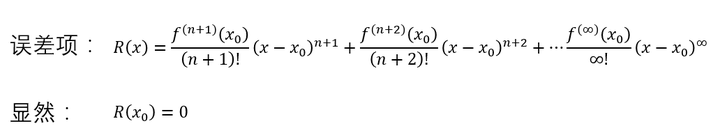：误差项中每一项都是俩数的乘积，假如是你，你肯定是想两边同时除掉一个，对吧，为了简单，把设为 :所以除过之后，就成了：等等，这一串东西看着怎么眼熟？咦？这不是柯西老哥推广的我的中值定理么？剩下的不就是……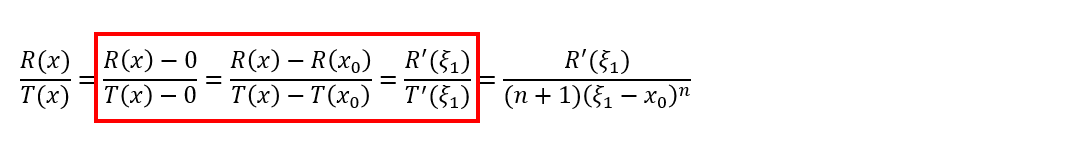：红框中，脑路之清奇、操作之风骚、画风之诡异、场面之震撼，让我们不禁感慨，拉格朗到底日了什么，脑海里才会想到柯西。拉格朗日写到这里卡住了，不知道你们有没有这种经验，反正我思考一道数学题的时候，会尝试着把思路进行到底，直到完全进了死胡同才会否定这种思路。有了前面的脑洞，拉格朗日继续复制这种思路，想看看能不能继续往下写：先看分子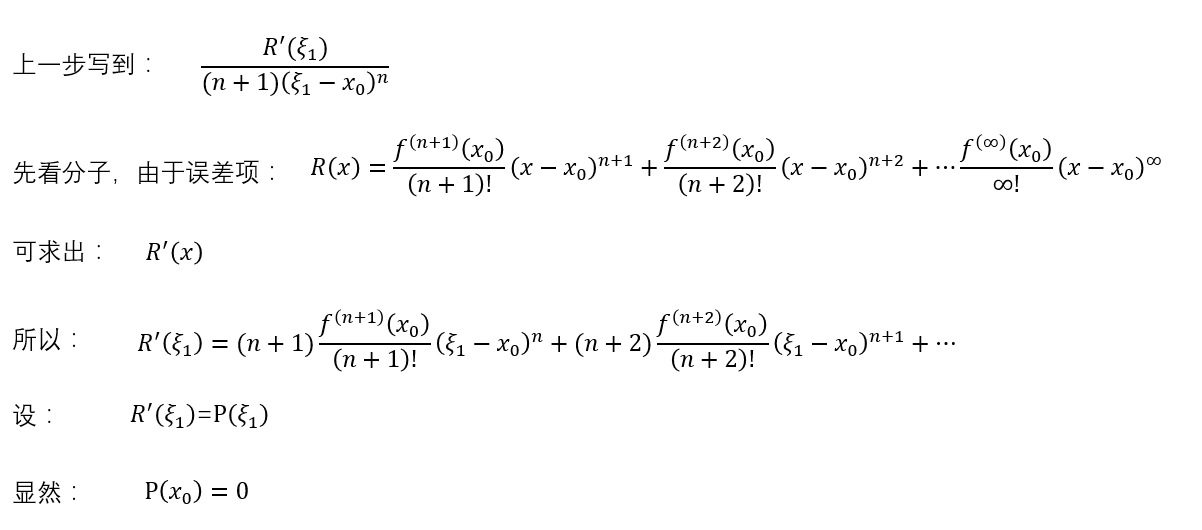再看分母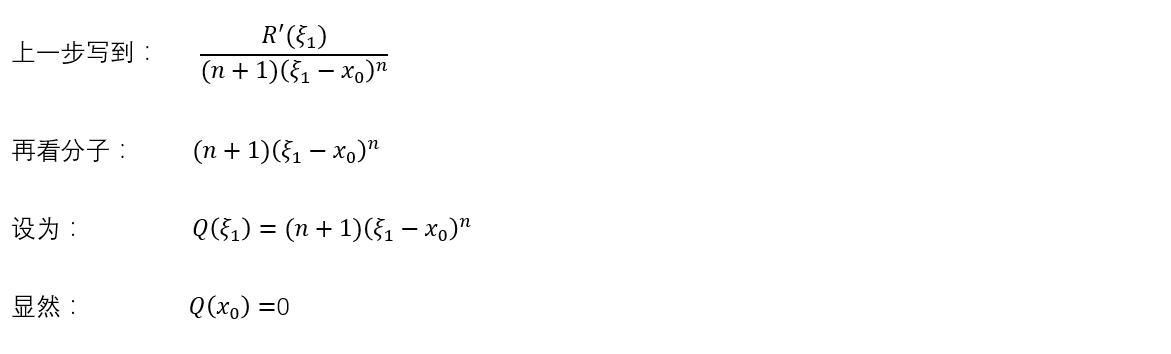好巧合，又可以用一次柯西的中值定理了。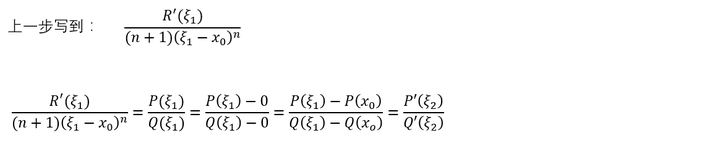总之，按照这种方法，可以一直求解下去，最终的结果就是：至此，拉格朗日把后面无数多的误差项给整合成了一项，而且比配诺亚更加先进的地方在于，不一定非要让趋近于，可以在二者之间的任何一个位置处展开，及其好用。

总结

数学家很有可能也是哲学家，遇到不懂的公式，尽量搜索一下其原理，这样也会便于理解和使用。