Beta分布及其应用

贝塔分布（Beta Distribution）是一个连续的概率分布，它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中，我们使用Beta分布作为描述。

原文地址：http://www.datalearner.com/blog/1051505532393058

一、Beta分布的定义及其简介

Beta分布是一个定义在[0,1]区间上的连续概率分布族，它有两个正值参数，称为形状参数，一般用 α \alpha和 β \beta表示。在贝叶斯推断中，Beta分布是Bernoulli、二项分布、负二项分布和几何分布的共轭先验分布。Beta分布的概率密度函数形式如下：

这里的 Γ \Gamma表示gamma函数。
Beta分布的均值是：

αα+β

\frac{\alpha}{\alpha+\beta}

方差是：

αβ(α+β)2(α+β+1)

\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}

下面我们看一下Beta分布的图形：
beta分布的R语言实例
　　首先，我们可以画一个beta分布的概率密度函数。

set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='probability density function',xlim=c(0,1),ylim=c(0,2.5),ylab='PDF')
lines(x,dbeta(x,0.5,0.5),col='red')
lines(x,dbeta(x,1,2),col='green')
lines(x,dbeta(x,2,2),col='pink')
lines(x,dbeta(x,2,5),col='orange')
lines(x,dbeta(x,1,3),col='blue')
lines(x,dbeta(x,5,1),col='black')
legend('top',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)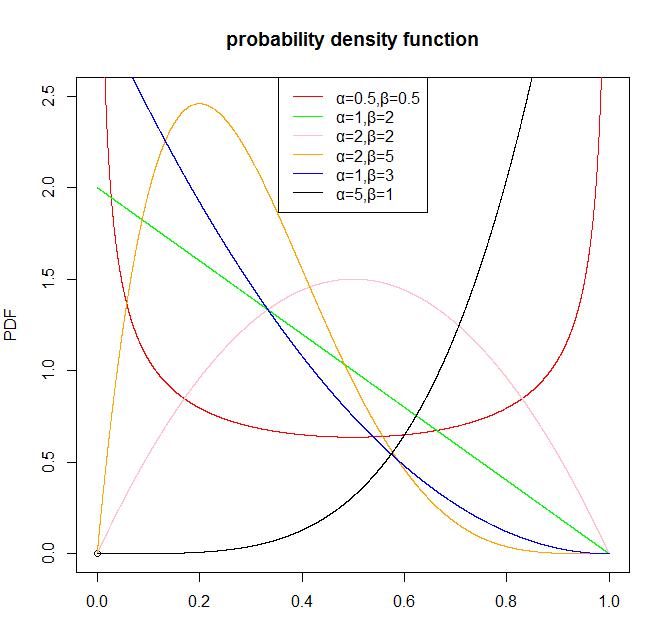

　　我们再来画一个beta分布的累计概率密度函数

set.seed(1)
x<-seq(0,1,length.out=10000)
plot(0,0,main='cumulative distribution function',xlim=c(0,1),ylim=c(0,1),ylab='PDF')
lines(x,pbeta(x,0.5,0.5),col='red')
lines(x,pbeta(x,1,2),col='green')
lines(x,pbeta(x,2,2),col='pink')
lines(x,pbeta(x,2,5),col='orange')
lines(x,pbeta(x,1,3),col='blue')
lines(x,pbeta(x,5,1),col='black')
legend('topleft',legend=c('α=0.5,β=0.5','α=1,β=2','α=2,β=2','α=2,β=5','α=1,β=3','α=5,β=1'),col=c('red','green','pink','orange','blue','black'),lwd=1)

从Beta分布的概率密度函数的图形我们可以看出，Beta分布有很多种形状，但都是在0-1区间内，因此Beta分布可以描述各种0-1区间内的形状（事件）。因此，它特别适合为某件事发生或者成功的概率建模。同时，当 α=1 \alpha=1， β=1 \beta=1的时候，它就是一个均匀分布。

下面我们使用三个例子来描述Beta分布的应用。

二、为实验成功概率建模（为棒球运动员的击球率建模）

Statlect网站上给出了一个简单的解释。假设一个概率实验只有两种结果，一个是成功，概率是 X X，另一个是失败，概率为(1−X)(1-X)。其中， X X的值我们是不知道的，但是它所有可能的情况也是等概率的。如果我们对XX的不确定性用一种方式描述，那么，可以认为 X X是一个来自于[0,1][0,1]区间的均匀分布的样本。这是很合理的，因为 X X只可能是[0,1][0,1]之间的某个值。同时，我们对 X X也一无所知，认为它是[0,1][0,1]之间任何一个可能的值。这些都与 [0,1] [0,1]均匀分布的性质契合。现在，假设我们做了 n n次独立重复的实验，我们观察到kk次成功， n−k n-k次失败。这时候我们就可以使用这些实验结果来修订之前的假设了。换句话说，我们就要计算 X X的条件概率，其条件是我们观察到的成功次数和失败次数。这里计算的结果就是Beta分布了。在这里，在总共nn次实验， k k次成功的条件下，XX的条件概率是一个Beta分布，其参数是 k+1 k+1和 n−k+1 n-k+1。

在Cross Validated的问题：What is the intuition behind beta distribution?中，David Robinson给出了另外一个关于击中棒球的例子。在棒球运动中，有个叫平均击球率的概念。就是用一个运动员击中棒球的次数除以他总的击球数量。一般情况下，棒球运动员的击球概率在 0.266 0.266左右。高于这个值就是不错的运动员了。假设我们要预测一个运动员在某个赛季的击球率，我们可以使用已有的数据计算。但是在赛季刚开始的时候，他击球次数少，因此无法准确预测。比如他只打了一次球，那击球率就是1或者0，这个显然是不对的，我们也不会这么预测。因为我们都有一个先验期望。即根据历史情况，我们认为一个运动员大概的击球率应当是在0.215到0.360之间。因此，当一个运动员在赛季开始就被三振出局，那么我们可以预期这个运动员的击球率可能会略低于平均值，但他不可能是0。那么，在这个运动员的例子中，关于在赛季开始的击球情况，可以使用二项式分布表示，也就是一系列击球成功和失败的实验（假设之间相互独立）。同时，我们也会给这个数据一个先验期望（即统计中的先验知识），这个先验的分布一般就是Beta分布。这里的Beta分布就是用来修正我们观测到的运动员的击球率的（简单来说就是即便开始这个运动员被三振出局了，我们也只会预测他的击球率可能低于平均水平，但不会是0）。

图1 Beta分布作为先验

如上图1所示，我们使用Beta分布作为先验来解决这个问题。这个图是这个问题的概率图模型，假设该用户的击球率的分布是一个参数为 θ \theta的分布（这里 θ \theta既表示一个分布，也是这个分布的参数。因为在概率图模型中，我们经常使用某个分布的参数来代替说明某个模型），也就是说 θ \theta是用户击球成功的概率。假设，到目前为止，用户在这个赛季总共打了 n n次球，击中的次数是xx，这是一个二项式分布，即 p(y|θ)=Binomial(x;n,θ) p(y|\theta) = \text{Binomial}(x;n,\theta)。我们的目标就是推导 θ \theta分布的形式并估算这个参数的值。这就变成了在贝叶斯推断中的求后验概率的问题了：

p(θ|y,α,β)=p(y|θ)p(θ|α,β)p(y)

p(\theta|y,\alpha,\beta)= \frac{p(y|\theta)p(\theta|\alpha,\beta)}{p(y)}

在这里，分母 p(y) p(y)是数据结果，也就是常数。分子第一个项是二项式分布，即 p(y|θ)=θx(1−θ)(n−x) p(y|\theta)=\theta^{x}(1-\theta)^{(n-x)}，分子的第二项是Beta分布的结果了。详细结果后面再说。在这里，最后我们会发现 θ \theta也是一个Beta分布。其结果为 Beta(α+x,β+(n−x)) \text{Beta}(\alpha+x,\beta+(n-x))

比如，假设所有的运动员击球率在0.27左右，范围一般是0.21到0.35之间。这个可以用参数 α=81 \alpha=81和 β=219 \beta=219的Beta分布表示，即 Beta(81,219) \text{Beta}(81,219)。为什么参数取这两个值呢？因为这两个参数的Beta分布的均值是0.27，主要的区间是[0.2,0.35]。假设某个用户击球300次，成功100次，那么，根据计算的结果，用户的击球率的分布应当是 Beta(181,419) \text{Beta}(181,419)，其概率大约是均值0.303，要比平均水平略高。

从上面这两个例子中我们可以看出，对于某个事件发生的可能的概率，当我们只有一些大概的了解，但无法知道确切的概率的时候，可以使用Beta分布表示这个概率分布。也就是说，Beta分布是用来为某些具有一定范围的事情建模的，例如0-1之间的概率。

三、为顺序统计量建模

假设有个机器可以随机产生[0,1]之间的随机数，机器运行10次，第7大的数是什么，偏离不超过0.01？这个问题的数学化表达如下：

X_1,X_2,...,X_n∼Uniform(0,1),i.i.d.

X\_{1},X\_{2},...,X\_{n} \sim Uniform(0,1),i.i.d.
　　2.将这n个随机变量排序得到顺序统计量

X_(1),X_(2),...,X_(n)

X\_{(1)},X\_{(2)},...,X\_{(n)}
　　3.问

X_(k)

X\_{(k)}的分布是什么？

　　我们可以假设计算

X_k

X\_{k}落在

[x,x+Δx]

[x,x+\Delta x]区间上的概率：

P(x≤Xk≤x+Δx)=?

P(x \leq X_{k} \leq x+\Delta x)=?
　　我们将区间分成三个部分

[0,x),[x,x+Δx],(x+Δx,1]

[0,x),[x,x+\Delta x],(x+\Delta x,1]。假设只有1个数落在区间

[x,x+Δx]

[x,x+\Delta x]内，那么该事件可以表示：

E={X1∈[x,x+Δx],Xi∈[0,x)],Xj∈(x+Δx,1]}

E=\{ X_{1} \in [x,x+\Delta x], X_{i} \in [0,x)] ,X_{j} \in (x+\Delta x,1]\}
　　其中，

i=2,...,k,j=k+1,...,n

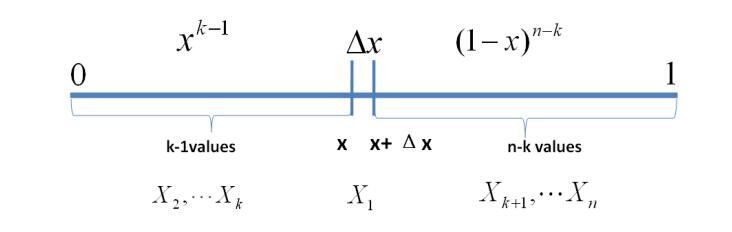
　　从而有：

P(E)=∏i=1nP(xi)=xk−1(1−x−Δx)n−kΔx=xk−1(1−x)n−kΔx+o(Δx)

P(E)=\prod_{i=1}^{n}P(x_{i})=x^{k-1}(1-x-\Delta x)^{n-k}\Delta x=x^{k-1}(1-x)^{n-k}\Delta x+o(\Delta x)
　　其中

o(Δx)

o(\Delta x)表示

Δx

\Delta x的高阶无穷小。根据推断，落在

[x,x+Δx]

[x,x+\Delta x]区间的事件超过一个，则对应的事件概率就是

o(Δx)

o(\Delta x)。进而我们可以得到

X_k

X\_{k}的概率密度为：

f(x)=limΔx→0P(x≤Xk≤x+Δx)Δx

f(x)=\lim_{\Delta x \to 0}\frac{P(x\leq X_{k}\leq x+\Delta x)}{\Delta x}

=n!(k−1)!(n−k)!xk−1(1−x)n−k

= \frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k}

=Γ(n+1)Γ(k)Γ(n−k+1)xk−1(1−x)n−k

= \frac{\Gamma(n+1)}{\Gamma(k)\Gamma(n-k+1)}x^{k-1}(1-x)^{n-k}

=Γ(α+β)Γ(α)Γ(β)xα−1(1−x)β−1

= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}
　　上式即为一般意义上的beta分布。具体的推导过程可以参见《LDA数学八卦》。

四、旧货商服务质量推断

假设亚马逊上有三家旧货商，其评价结果分别如下：

商家一：85193个评论，94%的正向
商家二：20785个评论，98%的正向
商家三：840个评论，99%的正向

那么这三个商家中，哪一家的服务质量最好呢？假设这三家的服务质量分别是 θX \theta_X、 θY \theta_Y和 θZ \theta_Z。假设我们对三家旧货商的信息一无所知，那么这些参数的先验可以认为是一个均匀分布，也可以等同于 beta(1,1) \text{beta}(1,1)。根据之前的知识，我们知道，最终这三家旧货商的服务质量应当服从三个不同参数的Beta分布，即 beta(80082,5113) \text{beta}(80082,5113)、 beta(20370,417) \text{beta}(20370,417)和 beta(833,9) \text{beta}(833,9)（把正向的和负向的评论书算出来，分别加1就是参数了，参考上面公式）。注意，当Beta分布的参数很大的时候，我们可以使用相同均值和方差的正态分布代替这个beta分布。因此，最终这三家供货商，商家3的服务质量的标准差是0.003，是最大的。其他两家的标准差比这个还小。因此，我们可以认为这三家供货商的服务质量都高度聚焦于他们的均值。因此，从第一个或第二个分布中抽取的样本不太可能比第三个样本的值高。也就是说前两个服务商不太可能质量比第三个高。

参考1：https://stats.stackexchange.com/questions/47771/what-is-the-intuition-behind-beta-distribution
参考2：https://www.johndcook.com/blog/2011/09/27/bayesian-amazon/#comments
参考3：https://en.wikipedia.org/wiki/Beta_distribution
参考4：《LDA数学八卦》