期末作业

物基一班　　陈天懿

学号：2013301020146

计算圆周率 蒙特卡罗方法 设计物理模型计算圆周率

摘要：

圆周率 是圆的周长与直径的比值，数学家已严格证明 是一个无理数。自从发现以来,它便成为了数学与物理学等自然科学中的重要常数，在生产生活中占有极为重要的地位。因此，如何精确计算圆周率就一直是人们研究的重要课题。如今，在高度发展的电子计算机的帮助下，圆周率 的计算速度和精度都达到了前所未有的高度。

本文利用python，分别从几何逼近，概率计算，幂级数展开直接计算和设计物理模型计算这4个角度探讨并实现了 的理论计算和数值模拟。前几个方法较为基础，本文重点在于最后一个方法，它同时也是物理理论模型和数值模拟拟合的一次成功尝试

背景：

是第十六个希腊字母的小写。 这个符号，亦是希腊语 περιφρεια (表示周边，地域，圆周等意思)的首字母。1706年英国数学家威廉·琼斯(William Jones ，1675－1749)最先使用“”来表示圆周率 。1736年，瑞士大数学家欧拉也开始用 表示圆周率。从此， 便成了圆周率的代名词。此后的几百年间，数学家们对 值更为精确的计算从未停止过。

正文：

计算圆周率的四种方法：几何逼近——割圆术：

早在公元263年，中国数学家刘徽用“割圆术”计算圆周率，原理就是：当圆内接多边形的边数无限增加时，多边形的周长和面积可以无限接近圆。他先从圆内接正六边形，逐次分割一直算到圆内接正192边形。他说“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这已包含了求极限的思想。刘徽给出 的圆周率近似值。

公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率 和约率 。在之后的800年里祖冲之计算出的π值都是最准确的。其中的密率在西方直到1573年才由德国人奥托(Valentinus Otho)得到，1625年发表于荷兰工程师安托尼斯(Metius)的著作中，欧洲称之为Metius' number。

已割圆术计算圆周率的具体思路如下：

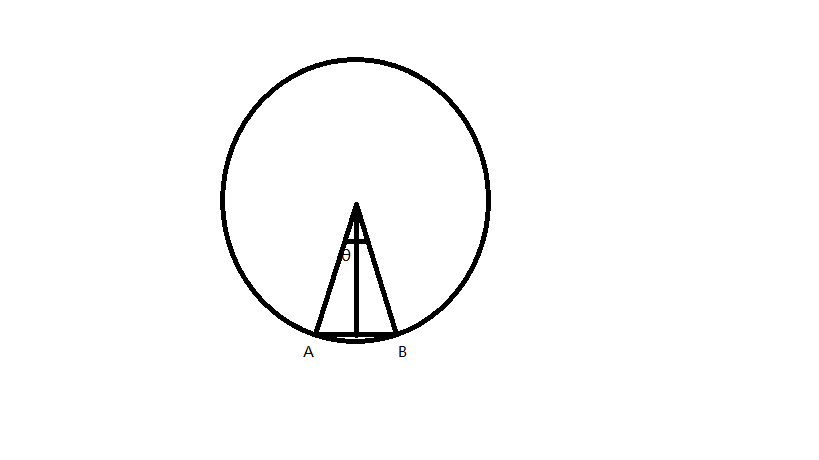
如图：这是一个圆和其内接正多边形的一部分，易知：

当 趋向于无穷大时，圆周长

So

计算结果如下：

…………

虽然这种方法的效率并不低，但是有一点极为严重：采用这种方法，我们必须事先知道 的值以计算 本身，这显然存在因果上的矛盾，因此这只能作为验证 值的手段，而不能作为计算 的方法。

概率法:

蒙特 · 卡罗方法 (Monte Carlo method)，也称统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。它的基本思想是：当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。

计算圆周率时，我们可以利用几何概型的概率原理，通过投点法算得投点扔进正方形内接圆内的频率估计这一概率的大小，亦即 的大小:

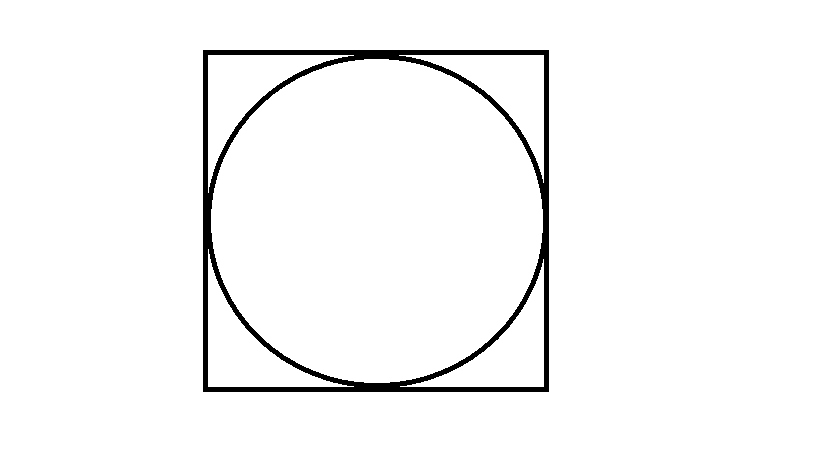
计算机模拟的效果如下：

代码如下

显然，频率并不直接等于概率，只是随着随机试验次数的增加，频率向着概率逼近，所以概率法的精度并不高。同时，因为计算机是根据随机数表生成的伪随机数，并不能保证每一个点能被随机取到，同时随着取的点越来越多，耗时越来越长，这些因素限制了此方法的精度和实用性。

幂级数展开直接计算:

说到 ，最先联想到的函数即为 利用微积分的知识，我们可以从反正切函数的泰勒级数得到 的逼近值：

取 即可一步一步计算 。但是这种方法的计算效率并不高，算至第10项才仅能获得前少数几位的精度。

因此，后人总结经验，又提出了许多精准快速的算法，圆周率的计算效率得以突破。

如：

bailey-borwein-plouffe算法：

这个公式简称BBP公式，由David Bailey, Peter Borwein和Simon Plouffe于1995年共同发表。它打破了传统的圆周率的算法，可以计算圆周率的任意第 位，而不用计算前面的 位。这为圆周率的分布式计算提供了可行性。

丘德诺夫斯基公式：

这是由丘德诺夫斯基兄弟发现的，十分适合计算机编程，是目前计算机使用较快的一个公式。

设计物理模型——小球的完全弹性碰撞和 的关系:

假设地面上有一堵墙，墙的右边某处有一物体B，它的右边某处又有一物体A。理想情况下地面无限长无限光滑，A，B两物体都可视为质点，AB之间，B和墙之间的碰撞都视为完全弹性碰撞。

假设B开始时静止。我们朝左推一下A，使A具有向左的初速度。

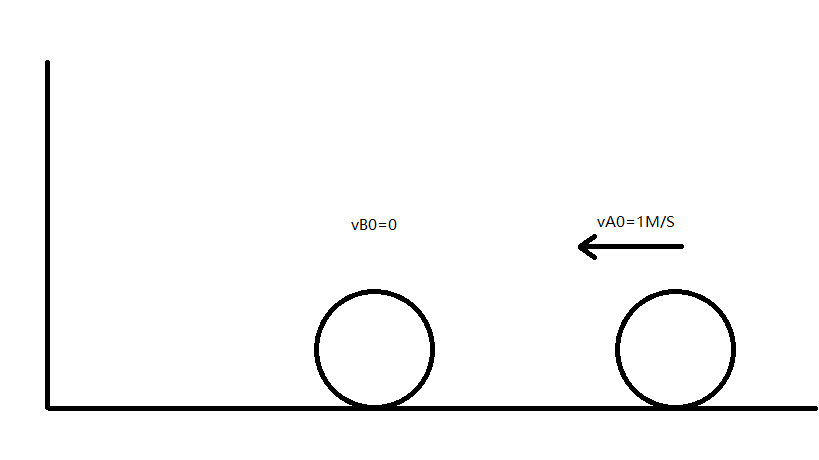
为了简化讨论，设水平向左为正方向，A获得的初速度为，物体A和B的质量比值为 ，即：

由动量和能量守恒，我们有可以推导碰撞之后的速度变化，设A和B第一次碰撞之后的速度为 ，，有动量能量守恒：

带入，化简并求解，可得：

在第一次试验中，我们令A与B质量相等，即 。 这样，A运动一段时间后撞到B(第一次)，由于动能守恒和动量守恒的缘故，A完全停止，而B以原先A的速度向左运动。B撞到墙(第二次)后以原速率向右弹回，运动后又撞到A(第三次)。接下去B完全停止，A向右一直运动。我们看到这样一共会发生3次碰撞。

我们发现次数和圆周率 的第一位数字一致，但如果仅从一次试验就断言碰撞次数和圆周率有着内在联系未免太牵强和不负责。因此我们继续试验。这时，我们保持其他假设不变，将A与B的质量比提高到100。即：

此时仅从计算分析得出碰撞次数就十分困难了，因此我们利用python进行迭代的数值模拟：

进行迭代的时候，只需对上面的速度公式进行略微变形，注意到B和墙碰撞之后速度反向，大小不变，则有：

为使公式进一步简洁，令

有:

碰撞结束的条件一定为：某次A和B碰撞后，A向右运动，B的速度大小小于A的速度大小。

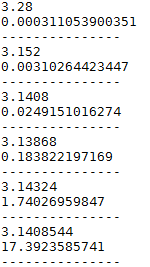
综合利用上述条件，我们通过数值模拟分别给出质量比 时总的碰撞次数：

真的就是：

3，

31，

314，

3141，

31415，

……

代码如下

显然为 的对应前几位数字。这可能让人感到惊奇！为什么会如此呢？显然这其中有着某种内在规律。

该实验最早在1995年由美国东伊利诺大学的数学家Gregory Galperin在一次关于小球碰撞的数学报告上提出。当他在报告中公布这个发现时，开始听众们都觉得难以置信。但在给出证明后，听众们又纷纷表示信服。

我们这次从几何角度给出更为直观的理论分析。

回到能量守恒：

亦即：

我们做一个拉伸变化，令

这意味着在任意时刻，点 都在单位圆 上。

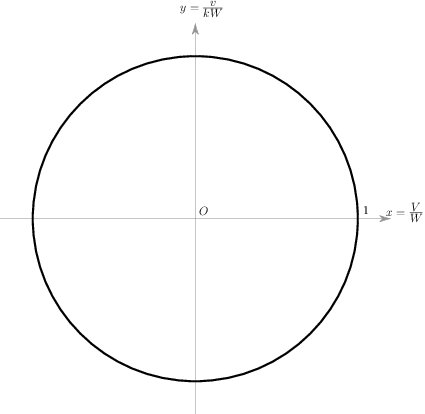
我们注意到，当在某段时间 到 之间没有发生过碰撞，那么这段时间里的 和 都是不变的，于是这段时间里点 也是不变的。在整个过程中只会发生有限次碰撞，所以 在坐标系中的图像将只有有限个点。下面我们将考察在某次碰撞前后，点 会怎样变化。

如果是物体B和墙的碰撞，那么在碰撞前B向左运动，碰撞后则向右运动，而速度大小相同；物体A则保持原来的运动状态。这意味着在碰撞前 处于 轴上方，碰撞后则处于 轴下方，和原来的点以 轴对称。

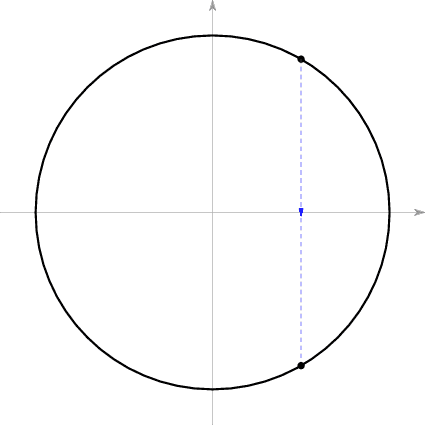
如果是物体A和B的碰撞，那么在碰撞前B必定静止或是在向右运动，不存在A和B都向左运动且A的速度大于B而与B相撞的可能，指出一点：如果B正在向左运动，表明前一次碰撞发生在A和B之间)，这意味着在碰撞前 处于 轴上或是在它的下方。碰撞前后动量守恒，即

化简：

亦即：

这意味着碰撞前后的 在同一条斜率为 的直线上。综合上述结论，碰撞前后的 的图像变化应该如下图所示，其中虚线的斜率为 。

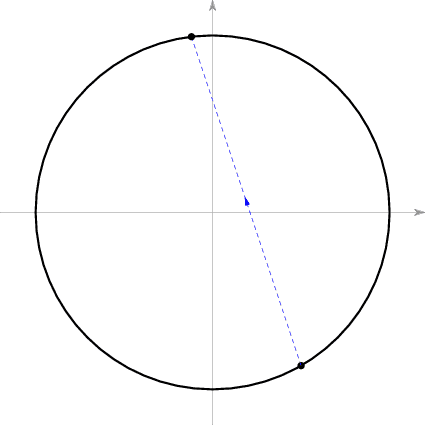
于是我们就得到了整个过程中 变换模式：从点 开始(对应着A刚开始以速度 向左运动，还未撞上B时的状态)，交替地以斜率为 的直线和以平行于y轴的直线成之字形在圆周上截出的点。下图是 的情形。每一条蓝色虚线段代表一次碰撞，箭头方向则代表了此次碰撞前后系统状态(即点 )转换的方向。

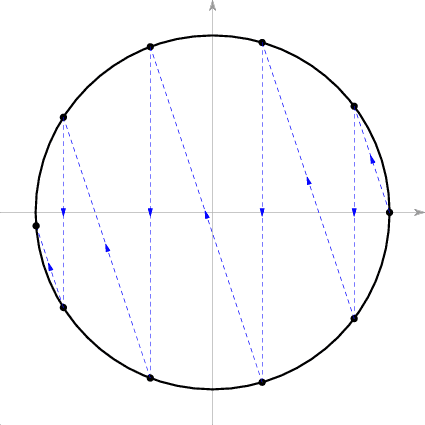
于是碰撞次数就是蓝色虚线段的数量，或者说是圆周上的 图像的点数减1。这样，一个物理问题被转化为一个几何问题：从点 开始，按照上述方法，交替地以斜率为 的直线和以平行于 轴的直线成之字形在圆周上截出的点会有几个？

顺便要指出的是，我们发现转换后的问题仅和 的值有关，或者说仅和物体B和物体A的质量比有关，而和物体A和物体B的具体质量、初始的推动速度W或是物体A和墙的距离等值无关。

接下来考察碰撞会在什么时候结束：

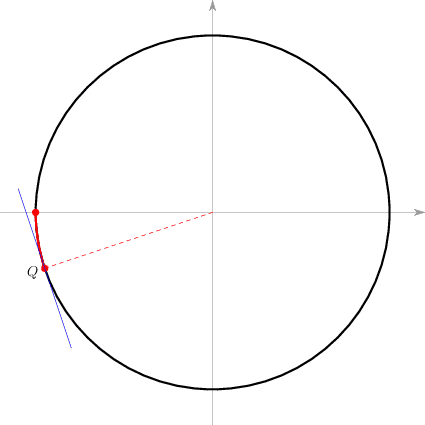
显然，不再发生碰撞的充要条件是物体A和物体B均处于静止或向右运动的状态，而且B的速率小于等于A的速率，即 ，且。翻译成 和 的关系，就是 ，对应到圆周上，就是下图里的红弧。因此，之字形截点过程终结，碰撞结束，当且仅当截点出现在上述的红弧上。

而截出终结点的方式有两种，下面我们分别讨论。

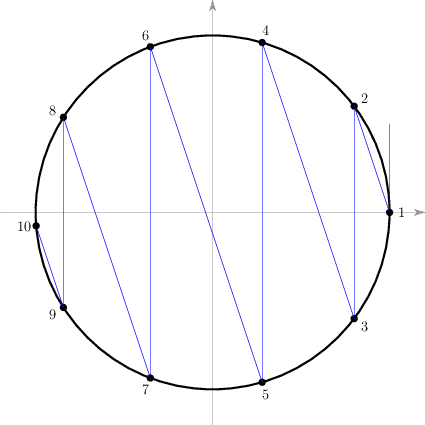
第一种方式是终结点被斜率为 的直线所截出。在物理上对应的过程是倒数第二次物体B和墙相撞向右弹回，并追上正向右运动的物体A，进行了最后一次撞击；撞击后物体A和B仍朝右运动，只是B的速率小于等于A。第一节中质量比为100的动画中的撞击过程就是这样结束的。在 时终结点也是这样被截出，下面我们以此为例说明。在图像中我们将每个点标了号，并通过初始点1作了切线。这样除了最后一点10外，每一点都对应着以它为顶点，由两条蓝色射线形成的角。因为所有斜率为 的直线都平行，所有平行于y轴的直线都平行，于是角1到角9依次两两都是平行直线的内错角，它们均相等，其正切是 ，故等于 。它们是圆周角(角1是弦切角，可以看作是圆周角的特殊情况)。从中学平面几何里我们知道，它们对应的圆弧长度均相等；因为圆半径为1，它们所对应的弧长是两倍的圆周角大小，即 。在 时，弧1-2、弧1-3、弧2-4、弧3-5、弧4-6、弧5-7、弧6-8、弧7-9，弧8-10的长度均是 ；而弧9-10的长度小于此值。出现最后这段弧长会等于前面的弧长的情况仅当终结点正好是点 ，这就是物体A和物体B质量相等的情况。

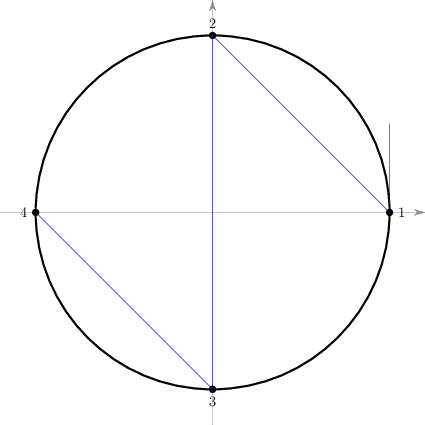
第二种方式是终结点被平行于 轴的直线所截出。在物理上对应的过程是倒数第二次物体B与物体A相撞后向左运动，最后撞在墙上向右弹回，但此时它的速率已小于A的速率，再也追不上A。这是第一节中质量比为10000的动画中的撞击过程结束的方式，同样也是 时的情况。下面我们以 为例说明。

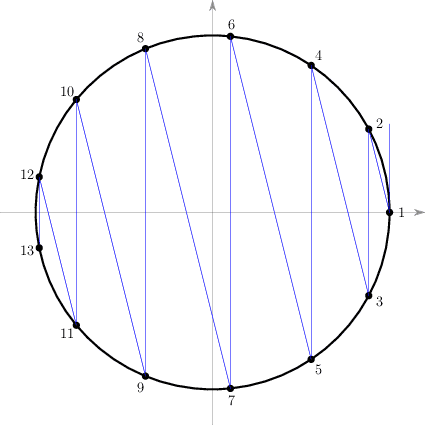
和 的情况很相似，圆上的截点把圆周截成了若干段长度为 的弧，以及最后一段弧12-13。最后这段弧的长度总是小于等于两倍的红弧(因为最后一点须在红弧内)，也就是 。

综合上述两种方式，我们就得到结论：之字形在半径为1的圆周上截出的点的个数，正是圆周的长度除以 的结果的整数部分再加1，这个1对应着那段比较短的弧。(严格地说，如果圆周的长度除以 的结果恰好是整数，如当k=1时，那么就不用加这个1了，这一点将在后面补充说明)。或者说，碰撞的次数(它等于点的个数减1)就是圆周的长度除以 的结果的整数部分。但半径为1的圆周的长度正是 。这一下，碰撞次数和圆周率的关系可谓昭然若揭，剩下的只不过是一点计算细节罢了。

碰撞的次数为圆周长 除以 的整数部分，也就是，其中 代表对 进行取整运算。当 时， 总比 大一点，但差不了多少；更精确地， 和 差不多大小， 越大，这个差就越小。这一点可对 在零点附近作泰勒展开并作估计即可，这里就不具体进行了。于是 和一般来说是相等的。

总的来说，在理论上 和 有极小的可能差1。一种可能是上述的圆周的长度除以 的结果恰好是整数的情况，因为 总比 大一点，于是 等于，正是圆周上的点个数减1。

另一种可能则相当麻烦。如果 和 恰好在某个整数的两侧，就如2.00001和1.99999在2的两侧那样，相差极少，取整结果却差1。但对于我们来说，即便 和 真的差1也不是太有所谓，因为这无非是在说，碰撞的次数和π的前几位数几乎一样，最多差1。这并不影响结果的漂亮，也不影响我们对为何初始的碰撞问题会和圆周率有出人意料却在数理之中的联系的理解。所以我们接下来就当这种可能性不存在。

这样我们就知道，总的碰撞次数是 。于是最终结论就显而易见了，在 时碰撞次数是 ， 时碰撞次数是 ，以此类推，它们就是圆周率 的对应位数的数字。

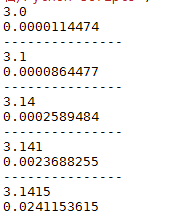
然而这种方法精确程度虽高，计算速度却很慢，本人电脑在算到 时便已无法继续。耗费的时间如图所示：

结论：

本文已四种方法从理论和数值模拟计算了圆周率的近似值，其中着重讲解和证明了完全弹性碰撞的两个小球和墙壁之间碰撞的总次数和 的深刻内在联系，虽然计算效率并不高，但重点在于实现理论和数值模拟的结合，从这点看最后一个方法具有重要意义。

参考文献：

百度百科圆周率词条；

Gary Antonick, The Pi Machine, Numberplay, Wordplay Blog, http://wordplay.blogs.nytimes.com/2014/03/10/pi/；

Gregory Galperin, Playing pool with π (the number π from a billiard point of view), Regular and Chaotic Dynamics, Volume 8, Number 4, Pages 375–394 (2003).