(以下内容搬运自 PaddleSpeech)

Derivative of CTC Loss

关于CTC的介绍已经有很多不错的教程了，但是完整的描述CTCLoss的前向和反向过程的很少，而且有些公式推导省略和错误。本文主要关注CTC Loss的梯度是如何计算的，关于CTC的介绍这里不做过多赘述，具体参看文末参考。

CTC主要应用于语音和OCR中，已语音Deepspeech2模型为例，CTC的网络一般如下图所示，包含softmax和CTCLoss两部分。反向传播需要求得loss L相对于logits u i u^i ui的梯度。下面先介绍CTCLoss的前向计算。

图片来源于文末参考

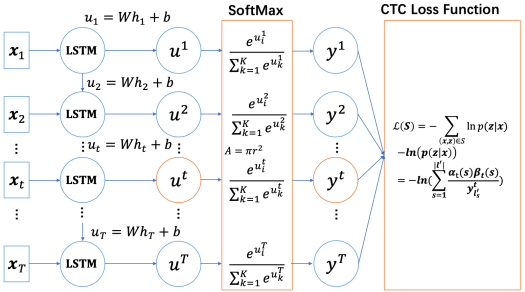
CTC Loss 的计算

CTC中path的定义与概率的计算如下：

path 是 $ L’^T$的元素，用 π \pi π表示。 x \textbf{x} x 是输入特征， y \textbf{y} y 是输出label，都是序列。 L L L 是输出的 vocab, L‘ 是 L ∪ b l a n k L \cup {blank} L∪blank。 y π t t y_{\pi_{t}}^t yπtt 表示在t时刻， π t \pi_{t} πt label时的观察概率。其中 π t \pi_{t} πt 表示 π \pi π path在t时刻的label。 π \pi π 是 y \textbf{y} y 与 x \textbf{x} x 的一个alignment，长度是 T T T，取值空间为 L ′ L' L′。path也称为alignment。

公式（2）解释了给定输入 x \textbf{x} x ，输出 π \pi π path 的概率，即从时间t=1到T每个时间点的概率 y π t t y_{\pi_{t}}^t yπtt 相乘。

求出单条path后，就可以计算 p ( l ∣ x ) p(l \mid x) p(l∣x) 的概率，计算如下：

这里边 B \mathcal{B} B 就是映射，即所有多对一的映射（many-to-one mapping )的集合。这样就算出来对应一个真正的 label l \textbf{l} l 的概率了，这里是求和。求和的原因就是 aab 和 abb 都是对应成ab, 所以 aab 的概率 + abb 的概率才是生成ab的概率。

公式（3）解释了给定输入 x \mathbf{x} x ，求输出 l \mathbf{l} l 的概率，即所有集合 B − 1 ( l ) \mathcal{B}^{-1} (\mathbf{l}) B−1(l) 中 path的概率和。

CTC forward-backward 算法

CTC的优化采用算最大似然估计MLE (maximum likelihood estimation), 这个和神经网络本身的训练过程是一致的。

这个CTC 计算过程类似HMM的 forward-backward algorithm，下面就是这个算法的推导过程：

上图中的定义很清楚，但是 α t − 1 ( s ) \alpha_{t-1}(s) αt−1(s) and α t − 1 ( s − 1 ) \alpha_{t-1}(s-1) αt−1(s−1) 和 α t ( s ) \alpha_t(s) αt(s) 的关系也不那么好看出来，下图给出了具体的关于 α t ( s ) \alpha_t(s) αt(s) 的推导过程：

这里的公式比较适合用下面的图来理解， α 1 ( 1 ) \alpha_1(1) α1(1) 其实对应的就是下图中左上角白色的圆圈。就是上来第一个是blank 的概率，而 α 1 ( 2 ) \alpha_1(2) α1(2)是label l 的第一个字母。这里边我们假设每个字母之间都插入了空白，即label l扩展成l’，例如，l=[a, b, b, c]， l’=[-, a, -, b, -, b, -, c, -]。然后对于其他圆点，在时间是1 的情况下概率都是 0. Figure 3中横轴是时间 t，从左到右是1到T；纵轴是s（sequence），从上到下是 1 到 ∣ l ′ ∣ \mathbf{\mid l' \mid} ∣l′∣.

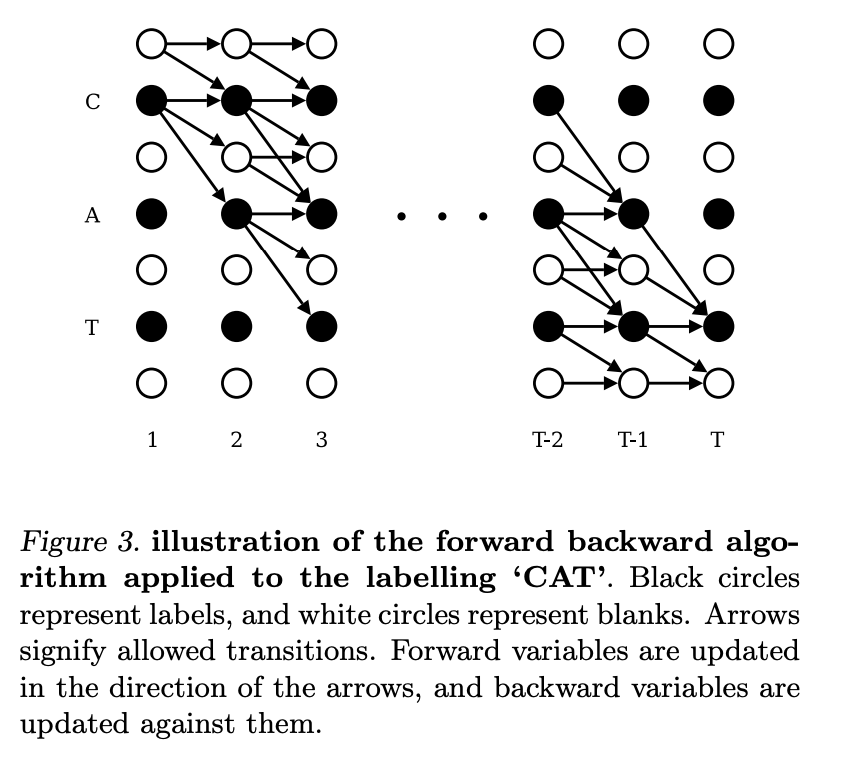
接下来我们分析递归公式 (resursion)，更多介绍可以参看 [2]. 公式6分情况考虑:

第一种情况就是当前的label是blank，或者 l ′ s = l ′ s − 2 \mathbf{l'}_{s}= \mathbf{l'}_{s-2} l′s=l′s−2(相邻是重复字符)：

这个时候他的概率来自于过去t-1的两个label 概率，也就是 a t − 1 ( s ) a_{t-1} (s) at−1(s) 和 a t − 1 ( s − 1 ) a_{t-1} (s-1) at−1(s−1) 。

a t − 1 ( s ) a_{t-1} (s) at−1(s) 就是说当前的 sequence 已经是 s 了，figure 3中表现为横跳， blank -->blank（例如t=3, s=3）；

而 a t − 1 ( s − 1 ) a_{t-1} (s-1) at−1(s−1)是说明当前的字符还不够，需要再加一个，所以在figure 3中就是斜跳，从黑色圆圈到白色圆圈（例如，t=3, s=5）。

仔细观察figure 3，除了第一排的白色圆圈，其他白色圆圈都有两个输入，就是上述的两种情况。当然判断blank 的方法也可以是判断 I s − 2 ′ = I s ′ I'_{s-2} = I'_{s} Is−2′=Is′. 这种情况也是说明 I s ′ I'_{s} Is′ 是blank, 因为每一个字符必须用 blank 隔开，即使是相同字符。

第二章情况也可以用类似逻辑得出，只不过当前的状态s 是黑色圆圈，有三种情况输入。

最终的概率就如公式8 所示，这个计算过程就是 CTC forward algroirthm，基于 Fig. 3 的左边的初始条件。

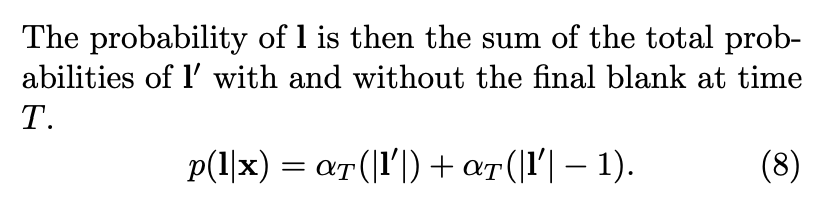
基于Fig. 3 右边的初始条件，我们还是可以计算出一个概率，那个就是 CTC backward. 这里我就不详细介绍了，直接截图。

这样一直做乘法，数字值越来越小，很快就会underflow。这个时候就需要做 scaling.

算出了forward probability 和 backward probability 有什么用呢，解释如下图。

上图是说 forward probability and backward probability 的乘积，代表了这个 sequence l \mathbf{l} l t时刻，是s label 的所有paths 的概率。这样的话我们就计算了 Fig. 3 中的每个圆圈的概率。为什么 α t ( s ) β t ( s ) \alpha_t(s)\beta_t(s) αt(s)βt(s) 中多出一个 y l s ′ t y^t_{\mathbf{l'_s}} yls′t ，这是因为它在 α \alpha α 和 β \beta β 中都包含该项，合并公式后就多出一项。

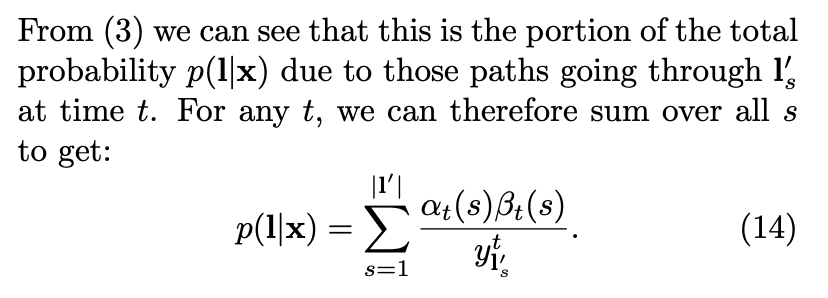
p ( l ∣ x ) p(\mathbf{l}|\mathbf{x}) p(l∣x) 可以通过任意时刻 t 的所有 s 的 foward-backward 概率计算得来。取负对数后就是单个样本的NLL（Negative Log Likelihood）。

总结

总结一下，根据前向概率计算CTCLoss函数，可以得出如下结论：

对于时序长度为T的输入序列x和输出序列z，前向概率：
α t ( s ) = ∑ π ∈ B − 1 ( z ) π t = l s ′ p ( π 1 : t ∣ x ) α 1 ( 1 ) = y − 1 ; α 1 ( 2 ) = y l 2 ′ 1 , α 1 ( s ) = 0 , ∀ s > 2 α t ( s ) = 0 , ∀ s < ∣ l ′ ∣ − 2 ( T − t ) − 1 , or ∀ s < 1 α t ( s ) = { ( α t − 1 ( s ) + α t − 1 ( s − 1 ) ) y l s ′ t if l s ′ = b or l s − 2 ′ = l s ′ ( α t − 1 ( s ) + α t − 1 ( s − 1 ) + α t − 1 ( s − 2 ) ) y l s ′ t otherwise \begin{split} \alpha_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{1:t}|x) \newline \alpha_1(1) &= y_{-}^1 ; \quad \alpha_1(2)=y^1_{l'_2}, \quad \alpha_1(s)=0, \forall s > 2 \newline \alpha_t(s) &= 0, \quad \forall s < |l'| - 2(T-t) - 1 ,\quad \text{or} \quad \forall s < 1 \newline \alpha_t(s) &= \begin{cases} (\alpha_{t-1}(s) + \alpha_{t-1}(s-1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s-2} = l'_s$} \newline (\alpha_{t-1}(s) + \alpha_{t-1}(s-1) + \alpha_{t-1}(s-2))y^t_{l'_s} & \text{otherwise}\newline \end{cases} \end{split} αt(s)α1(1)αt(s)αt(s)=πt=ls′π∈B−1(z)∑p(π1:t∣x)=y−1;α1(2)=yl2′1,α1(s)=0,∀s>2=0,∀s<∣l′∣−2(T−t)−1,or∀s<1={(αt−1(s)+αt−1(s−1))yls′t(αt−1(s)+αt−1(s−1)+αt−1(s−2))yls′tif ls′=b or ls−2′=ls′otherwise
利用 α t ( s ) \alpha_t(s) αt(s) 计算CTCLoss：
− l n ( p ( l ∣ x ) ) = − l n ( α T ( ∣ l ′ ∣ ) + α T ( ∣ l ′ ∣ − 1 ) ) -ln(p(l \mid x)) = -ln(\alpha_{T}(|l'|)+\alpha_{T}(|l'|-1)) −ln(p(l∣x))=−ln(αT(∣l′∣)+αT(∣l′∣−1))

根据后向概率计算CTCLoss函数，可以得出如下结论：

对于时序长度为T的输入序列x和输出序列z，后向概率：
β t ( s ) = ∑ π ∈ B − 1 ( z ) π t = l s ′ p ( π t : T ∣ x ) β T ( ∣ l ′ ∣ ) = y − T ; β T ( ∣ l ′ ∣ − 1 ) = y l ∣ l ′ ∣ − 1 ′ T , β T ( s ) = 0 , ∀ s < ∣ l ′ ∣ − 1 β t ( s ) = 0 , ∀ s > 2 t or ∀ s < ∣ l ′ ∣ β t ( s ) = { ( β t + 1 ( s ) + β t + 1 ( s + 1 ) ) y l s ′ t if l s ′ = b or l s + 2 ′ = l s ′ ( β t + 1 ( s ) + β t + 1 ( s + 1 ) + β t + 1 ( s + 2 ) ) y l s ′ t otherwise \begin{split} \beta_t(s) &= \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(z)} } p(\pi_{t:T}|x) \newline \beta_T(|l'|) &= y_{-}^T ; \quad \beta_T(|l'|-1)=y^T_{l'_{|l'|-1}}, \quad \beta_T(s)=0, \forall s < |l'| - 1 \newline \beta_t(s) &= 0, \text{$\forall s > 2t$ or $\forall s < |l'|$} \newline \beta_t(s) &= \begin{cases} (\beta_{t+1}(s) + \beta_{t+1}(s+1) ) y^t_{l'_s} & \text{if $l'_s=b$ or $l'_{s+2} = l'_s$} \newline (\beta_{t+1}(s) + \beta_{t+1}(s+1) + \beta_{t+1}(s+2))y^t_{l'_s} & \text{otherwise}\newline \end{cases} \end{split} βt(s)βT(∣l′∣)βt(s)βt(s)=πt=ls′π∈B−1(z)∑p(πt:T∣x)=y−T;βT(∣l′∣−1)=yl∣l′∣−1′T,βT(s)=0,∀s<∣l′∣−1=0,∀s>2t or ∀s<∣l′∣={(βt+1(s)+βt+1(s+1))yls′t(βt+1(s)+βt+1(s+1)+βt+1(s+2))yls′tif ls′=b or ls+2′=ls′otherwise
利用 β t ( s ) \beta_t(s) βt(s)计算CTCLoss：

− l n ( p ( l ∣ x ) ) = − l n ( β 1 ( 1 ) + β 1 ( 2 ) ) -ln(p(l \mid x)) = -ln(\beta_{1}(1)+\beta_{1}(2)) \newline −ln(p(l∣x))=−ln(β1(1)+β1(2))

根据任意时刻的前向概率和后向概率计算CTC Loss函数，得到如下结论：

对于任意时刻t，利用前向概率和后向概率计算CTCLoss：

p ( l ∣ x ) = ∑ s = 1 ∣ l ′ ∣ α t ( s ) β t ( s ) y l s ′ t − l n ( p ( l ∣ x ) ) = − l n ( ∑ s = 1 ∣ l ′ ∣ α t ( s ) β t ( s ) y l s ′ t ) p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \newline -ln(p(l \mid x)) = -ln( \sum_{s=1}^{|l'|} \frac{\alpha_t(s) \beta_t(s)}{y_{l'_s}^t} ) p(l∣x)=s=1∑∣l′∣yls′tαt(s)βt(s)−ln(p(l∣x))=−ln(s=1∑∣l′∣yls′tαt(s)βt(s))
我们已经得到CTCLoss的计算方法，接下来对其进行求导。

CTC梯度计算

微分公式

在计算梯度前，我们先回顾下基本的微分公式：
C ′ = 0 x ′ = 1 x n = n ⋅ x n − 1 ( e x ) ′ = e x l o g ( x ) ′ = 1 x ( u + v ) ′ = u ′ + v ′ ( u v ) ′ = u ′ v − u v ′ v 2 d f ( g ( x ) ) d x = d f ( g ( x ) ) d g ( x ) ⋅ d g ( x ) d x C' = 0 \\ x' = 1 \newline x^n = n \cdot x^{n-1} \newline (e^x)' = e^x \newline log(x)' = \frac{1}{x} \newline (u + v)' = u' + v' \newline (\frac{u}{v})' = \frac{u'v-uv'}{v^2} \newline \frac{\mathrm{d}f(g(x))}{\mathrm{d}x} = \frac{\mathrm{d}f(g(x))}{\mathrm{d}g(x)} \cdot \frac{\mathrm{d}g(x)}{\mathrm{d}x} C′=0x′=1xn=n⋅xn−1(ex)′=exlog(x)′=x1(u+v)′=u′+v′(vu)′=v2u′v−uv′dxdf(g(x))=dg(x)df(g(x))⋅dxdg(x)

CTC梯度

最大似然估计训练就是最大化训练集中每一个分类的对数概率，即最小化Eq. 12。

最后就是算微分了，整个推导过程就是加法和乘法，都可以微分。 O M L \mathit{O}^{ML} OML关于神经网络的输出 y k t y^t_k ykt的梯度见Eq. 13。因为训练样本是相互独立的，所以可以单独考虑每个样本，公式如Eq.13。

下面是CTCLoss的梯度计算：

### CTC梯度推导

回顾下之前的公式，便于理解后续推导过程。

p ( l ∣ x ) = ∑ s = 1 ∣ l ′ ∣ α t ( s ) β t ( s ) y l s ′ t α t ( s ) β t ( s ) = ∑ π ∈ B − 1 ( l ) : π t = l s ′ y l s ′ t ∏ t = 1 T y π t t p(l \mid x) = \sum_{s=1}^{|l'|} \frac{\alpha_t(s)\beta_t(s)}{y_{l'_s}^t} \\ \begin{equation} \alpha_t(s) \beta_t(s) = \sum_{ \underset{\pi_t=l'_s}{\pi \in \mathcal{B}^{-1}(l):} } y^t_{l'_s} \prod_{t=1}^T y^t_{\pi_t} \end{equation} p(l∣x)=s=1∑∣l′∣yls′tαt(s)βt(s)αt(s)βt(s)=πt=ls′π∈B−1(l):∑yls′tt=1∏Tyπtt

其中Eq. 15的计算过程如下：

∂ p ( l ∣ x ) ∂ y k t = ∑ s ∈ l a b ( z , k ) ∂ α t ( s ) β t ( s ) y k t ∂ y k t = ∑ s ∈ l a b ( z , k ) ( α t ( s ) β t ( s ) ) ’ y k t − α t ( s ) β t ( s ) y k t ′ y k t 2 = ∑ s ∈ l a b ( z , k ) ( ∏ t ′ = 1 t − 1 y π t ′ t ′ ⋅ y k t ⋅ y k t ⋅ ∏ t ′ = t + 1 T y π t ′ t ′ ) ’ y k t − α t ( s ) β t ( s ) y k t ′ y k t 2 = ∑ s ∈ l a b ( z , k ) 2 α t ( s ) β t ( s ) − α t ( s ) β t ( s ) y k t 2 = ∑ s ∈ l a b ( z , k ) α t ( s ) β t ( s ) y k t 2 = 1 y k t 2 ∑ s ∈ l a b ( z , k ) α t ( s ) β t ( s ) \begin{align*} \frac{\partial p( l \mid x)}{\partial y_k^t} & = \sum_{s \in lab(z,k)} \frac{ \partial \frac{ \alpha_t(s) \beta_t(s)}{y_{k}^t}}{\partial y_k^t} \newline & = \sum_{s \in lab(z,k)} \frac{(\alpha_t(s)\beta_t(s))’y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2} \newline &= \sum_{s \in lab(z,k)} \frac{( \prod_{t'=1}^{t-1} y^{t'}_{\pi_{t'}} \cdot y_k^t \cdot y_k^t \cdot \prod_{t'=t+1}^{T} y^{t'}_{\pi_{t'}} )’ y_k^t - \alpha_t(s)\beta_t(s){y_k^t}'}{{y_k^t}^2} \newline &= \sum_{s \in lab(z,k)} \frac{2\alpha_t(s)\beta_t(s) - \alpha_t(s)\beta_t(s)}{{y_k^t}^2} \newline &= \sum_{s \in lab(z,k)} \frac{\alpha_t(s)\beta_t(s)}{{y_k^t}^2} \newline &= \frac{1}{{y_k^t}^2} \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \tag{1} \newline \end{align*} ∂ykt∂p(l∣x)=s∈lab(z,k)∑∂ykt∂yktαt(s)βt(s)=s∈lab(z,k)∑ykt2(αt(s)βt(s))’ykt−αt(s)βt(s)ykt′=s∈lab(z,k)∑ykt2(∏t′=1t−1yπt′t′⋅ykt⋅ykt⋅∏t′=t+1Tyπt′t′)’ykt−αt(s)βt(s)ykt′=s∈lab(z,k)∑ykt22αt(s)βt(s)−αt(s)βt(s)=s∈lab(z,k)∑ykt2αt(s)βt(s)=ykt21s∈lab(z,k)∑αt(s)βt(s)(1)

NLL的公式推导如下：
∂ l n ( p ( l ∣ x ) ) ∂ y k t = 1 p ( l ∣ x ) ∂ p ( l ∣ x ) ∂ y k t = 1 p ( l ∣ x ) y k t 2 ∑ s ∈ l a b ( z , k ) α t ( s ) β t ( s ) (2) \begin{split} \frac{\partial {ln(p(l \mid x))} }{ \partial y^t_k } &= \frac{1}{p(l \mid x)} \frac{ \partial{p(l \mid x)} }{ \partial y_k^t } \newline &= \frac{1}{p(l \mid x) {y^t_k}^2 } \sum_{s \in lab(z,k)} \alpha_t(s)\beta_t(s) \end{split} \tag{2} ∂ykt∂ln(p(l∣x))=p(l∣x)1∂ykt∂p(l∣x)=p(l∣x)ykt21s∈lab(z,k)∑αt(s)βt(s)(2)

已经算出了CTCLoss对于 y k t y_k^t ykt 的梯度，接下来我们需要计算 CTCLoss对于 u k t u^t_k ukt（logits）的梯度。套用链式法则，并替换 y k t y^t_k ykt 为 y k ′ t y^t_{k'} yk′t，结果如下图。图中 k ′ k' k′ 表示vocab中的某一个token， K K K 是vocab的大小。

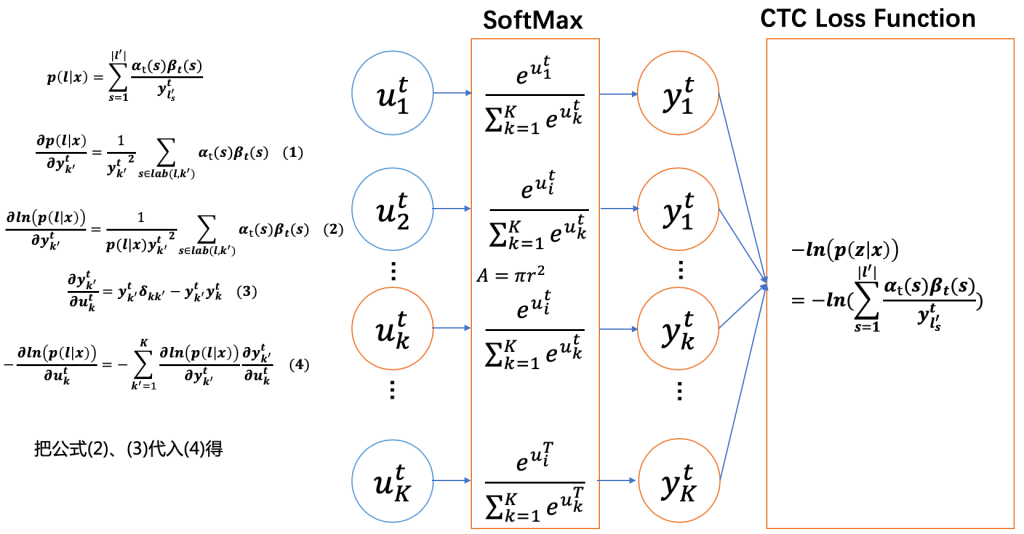
图中公式4根据链式法则得到：
$$

\frac{ \partial ln(p(l \mid x)) }{ \partial u^t_k }
= - \sum_{k’=1}^{K} \frac{ \partial ln(p(l \mid x)) }{ \partial y^t_{k’} } \frac{ \partial y^t_{k’} }{ \partial u^t_k } \tag{4}
$$

图中公式3是softmax的梯度，参考 [4]，计算过程如下：
s o f t m a x ( j ) = S j = e a j ∑ k = 1 K e a k , ∀ j ∈ 1 … K softmax(j) = S_j = \frac{ e^{a_j} }{ \sum_{k=1}^K e^{a_k} }, \enspace \forall j \in 1 \dots K softmax(j)=Sj=∑k=1Keakeaj,∀j∈1…K

∂ S i ∂ a j = ∂ ( e a i ∑ k e a k ) ∂ a j = { e i a ∑ − e j a e i a ∑ 2 = e i a ∑ ∑ − e j a ∑ = S i ( 1 − S j ) i = j, ∑ stands for ∑ k = 1 K e k a 0 − e j a e i a ∑ 2 = − e j a ∑ e i a ∑ = − S j S i i ≠ j, ∑ stands for ∑ k = 1 K e k a = { S i ( 1 − S j ) i = j − S j S i = S i ( 0 − S j ) i ≠ j = S i ( δ i j − S j ) (3) \begin{split} \frac{ \partial S_i }{ \partial a_j} &= \frac{ \partial (\frac{ e^{ a_i } }{ \sum_k e^{ a_k } }) } { \partial a_j } \newline &= \begin{cases} \frac{ e^a_i \sum - e^a_j e^a_i }{ \sum^2 } &= \frac{ e^a_i }{ \sum } \frac{ \sum - e^a_j }{ \sum } \newline &= S_i(1-S_j) & \text{i = j, $\sum$ stands for $\sum_{k=1}^K e^a_k$} \newline \frac{ 0 - e^a_j e^a_i }{ \sum^2 } &= - \frac{ e^a_j }{ \sum } \frac{ e^a_i }{ \sum } \newline &= -S_j S_i & \text{i $\neq$ j, $\sum$ stands for $\sum_{k=1}^K e^a_k$} \end{cases} \newline &= \begin{cases} S_i(1 - S_j) & \text{$i = j$} \newline -S_j S_i = S_i (0 - S_j) & \text{$i \neq j$} \end{cases} \newline &= S_i (\delta_{ij} - S_j ) \end{split} \tag{3} ∂aj∂Si=∂aj∂(∑keakeai)=⎩ ⎨ ⎧∑2eia∑−ejaeia∑20−ejaeia=∑eia∑∑−eja=Si(1−Sj)=−∑eja∑eia=−SjSii = j, ∑ stands for ∑k=1Kekai = j, ∑ stands for ∑k=1Keka={Si(1−Sj)−SjSi=Si(0−Sj)i=ji=j=Si(δij−Sj)(3)
δ i j = { 1 if i = j 0 otherwise \delta_{ij} = \begin{cases} 1 & \text{if i = j} \newline 0 & \text{otherwise} \end{cases} δij={10if i = jotherwise

下图中黄色框中的部分表示公式（1），即遍历所有的vocab中的token，其结果是 p ( l ∣ x ) p(l \mid x) p(l∣x)。这是因为label l l l 中的token一定在vocab中，且 s ∈ l a b ( l , k ′ ) s \in lab(l, k') s∈lab(l,k′) 可以是空集。当 k ′ k' k′ 在 l 中，s 则为label中token是 k ′ k' k′的概率；当 k ′ k' k′不在l中，s为空，概率为0。

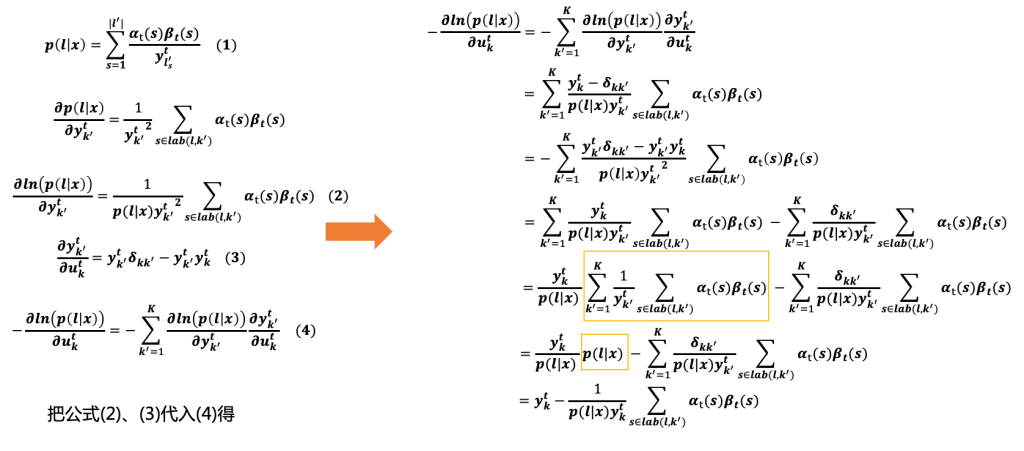
公式（2），（3）带入（4），并结合公式（1）的结果如上图右边，即：
− ∂ l n ( p ( l ∣ x ) ) ∂ u k t = − ∑ k ′ = 1 K ∂ l n ( p ( l ∣ x ) ) ∂ y k ′ t ∂ y k ′ t ∂ u k t = − ∑ k ′ = 1 K y k ′ t ( δ k k ′ − y k t ) p ( l ∣ x ) y k ′ t 2 ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = − ∑ k ′ = 1 K δ k k ′ − y k t p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = ∑ k ′ = 1 K y k t − δ k k ′ p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = ∑ k ′ = 1 K y t p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) − ∑ k ′ = 1 K δ k k ′ p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = y k t p ( l ∣ x ) ( ∑ k ′ = 1 K 1 y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) ) − ∑ k ′ = 1 K δ k k ′ p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = y k t p ( l ∣ x ) p ( l ∣ x ) − ∑ k ′ = 1 K δ k k ′ p ( l ∣ x ) y k ′ t ∑ s ∈ l a b ( l , k ′ ) α t ( s ) β t ( s ) = y k t − 1 p ( l ∣ x ) y k t ∑ s ∈ l a b ( l , k ) α t ( s ) β t ( s ) \begin{split} - \frac{ \partial ln(p(l \mid x)) }{ \partial u^t_k } &= - \sum_{k'=1}^K \frac{ \partial ln(p(l \mid x)) }{ \partial y^t_{k'} } \frac{ \partial y^t_{k'}}{ \partial u^t_k } \newline &= - \sum_{k'=1}^K \frac{ y^t_{k'}( \delta_{kk'} - y^t_k ) }{ p(l \mid x) {y^t_{k'}}^2 } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= - \sum_{k'=1}^K \frac{ \delta_{kk'} - y^t_k }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= \sum_{k'=1}^K \frac{ y^t_k - \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= \sum_{k'=1}^K \frac{ y^t }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= \frac{ y^t_k }{ p(l \mid x) } ( \sum_{k'=1}^K \frac{1}{y^t_{k'}} \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) ) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= \frac{ y^t_k }{ p(l \mid x) } p(l \mid x) - \sum_{k'=1}^K \frac{ \delta_{kk'} }{ p(l \mid x) y^t_{k'} } \sum_{s \in lab(l, k') } \alpha_t(s) \beta_t(s) \newline &= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline \end{split} −∂ukt∂ln(p(l∣x))=−k′=1∑K∂yk′t∂ln(p(l∣x))∂ukt∂yk′t=−k′=1∑Kp(l∣x)yk′t2yk′t(δkk′−ykt)s∈lab(l,k′)∑αt(s)βt(s)=−k′=1∑Kp(l∣x)yk′tδkk′−ykts∈lab(l,k′)∑αt(s)βt(s)=k′=1∑Kp(l∣x)yk′tykt−δkk′s∈lab(l,k′)∑αt(s)βt(s)=k′=1∑Kp(l∣x)yk′tyts∈lab(l,k′)∑αt(s)βt(s)−k′=1∑Kp(l∣x)yk′tδkk′s∈lab(l,k′)∑αt(s)βt(s)=p(l∣x)ykt(k′=1∑Kyk′t1s∈lab(l,k′)∑αt(s)βt(s))−k′=1∑Kp(l∣x)yk′tδkk′s∈lab(l,k′)∑αt(s)βt(s)=p(l∣x)yktp(l∣x)−k′=1∑Kp(l∣x)yk′tδkk′s∈lab(l,k′)∑αt(s)βt(s)=ykt−p(l∣x)ykt1s∈lab(l,k)∑αt(s)βt(s)

最终，为了通过softmax层传播CTCLoss的梯度，需要计算目标函数与 logits u k t u^t_k ukt 的偏微分，即Eq. 16:

α ^ t ( s ) = d e f α t ( s ) C t , C t = d e f ∑ s α t ( s ) β ^ t ( s ) = d e f β t ( s ) D t , D t = d e f ∑ s β t ( s ) − ∂ l n ( p ( l ∣ x ) ) ∂ u k t = y k t − 1 y k t ∑ s = 1 ∣ l ′ ∣ α ^ t ( s ) β ^ t ( s ) y l s ′ t ∑ s ∈ l a b ( l , k ) α ^ t ( s ) β ^ t ( s ) \begin{align*} \hat{\alpha}_t(s) & \overset{def}{=} \frac{ \alpha_t(s) }{ C_t } ,\enspace C_t \overset{def}{=} \sum_s \alpha_t(s) \newline \hat{\beta}_t(s) & \overset{def}{=} \frac{ \beta_t(s) }{ D_t } ,\enspace D_t \overset{def}{=} \sum_s \beta_t(s) \newline - \frac{ \partial ln(p(l \mid x)) }{ \partial u^t_k } &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \tag{16} \newline \end{align*} α^t(s)β^t(s)−∂ukt∂ln(p(l∣x))=defCtαt(s),Ct=defs∑αt(s)=defDtβt(s),Dt=defs∑βt(s)=ykt−ykt∑s=1∣l′∣yls′tα^t(s)β^t(s)1s∈lab(l,k)∑α^t(s)β^t(s)(16)

总结

通过动态规划算法计算 α t ( s ) \alpha_t(s) αt(s) 和 β t ( s ) \beta_t(s) βt(s)
通过 α t ( s ) \alpha_t(s) αt(s) 计算 p ( l ∣ x ) = α T ( ∣ l ′ ∣ ) + α T ( ∣ l ′ ∣ − 1 ) p(l \mid x)=\alpha_T(\mid l' \mid) + \alpha_T(\mid l' \mid -1) p(l∣x)=αT(∣l′∣)+αT(∣l′∣−1)
通过 α t ( s ) \alpha_t(s) αt(s) 和 β t ( s ) \beta_t(s) βt(s)
计算CTcLoss函数的导数:

− ∂ l n ( p ( l ∣ x ) ) ∂ u k t = y k t − 1 p ( l ∣ x ) y k t ∑ s ∈ l a b ( l , k ) α t ( s ) β t ( s ) = y k t − 1 y k t ∑ s = 1 ∣ l ′ ∣ α ^ t ( s ) β ^ t ( s ) y l s ′ t ∑ s ∈ l a b ( l , k ) α ^ t ( s ) β ^ t ( s ) (16) \begin{split} - \frac{ \partial ln(p(l \mid x)) }{ \partial u^t_k } &= y^t_k - \frac{ 1 }{ p(l \mid x) y^t_k } \sum_{s \in lab(l, k)} \alpha_t(s) \beta_t(s) \newline &= y^t_k - \frac{1}{y^t_k \sum_{s=1}^{\mid l' \mid} \frac{ \hat{\alpha}_t(s) \hat{\beta}_t(s) }{ y^t_{l'_s} } } \sum_{s \in lab(l, k)} \hat{\alpha}_t(s) \hat{\beta}_t(s) \newline \end{split} \tag{16} −∂ukt∂ln(p(l∣x))=ykt−p(l∣x)ykt1s∈lab(l,k)∑αt(s)βt(s)=ykt−ykt∑s=1∣l′∣yls′tα^t(s)β^t(s)1s∈lab(l,k)∑α^t(s)β^t(s)(16)

P.S. 欢迎关注我们的 github repo PaddleSpeech, 是基于飞桨 PaddlePaddle 的语音方向的开源模型库，用于语音和音频中的各种关键任务的开发，包含大量基于深度学习前沿和有影响力的模型。

语音识别 CTC Loss相关推荐

语音识别：深入理解CTC Loss原理
最近看了百度的Deep Speech,看到语音识别使用的损失函数是CTC loss.便整理了一下有关于CTC loss的一些定义和推导.由于个人水平有限,如果文章有错误,还恳请各位指出,万分感谢~ ...
深入浅出CTC loss
前言本片博客主要学习了CTC并在动态规划求CTC loss的理解上学习了这篇博客由于在看的过程中,还是花了很长时间反复推敲作者的理解,因此在这边用更加简单的话来解释一下CTC loss 背 ...
【项目实践】中英文文字检测与识别项目（CTPN+CRNN+CTC Loss原理讲解）
点击上方"小白学视觉",选择加"星标"或"置顶" 重磅干货,第一时间送达本文转自:opencv学堂 OCR--简介文字识别也是图像领域一 ...
DL之CNN：利用CNN(keras, CTC loss, {image_ocr})算法实现OCR光学字符识别
DL之CNN:利用CNN(keras, CTC loss)算法实现OCR光学字符识别目录输出结果实现的全部代码输出结果更新-- 实现的全部代码部分代码源自:GitHub https://r ...
CTC Loss (一）
论文:https://mediatum.ub.tum.de/doc/1292048/file.pdf 在文本识别模型CRNN中,一张包含单行文本的图片输入模型经过CNN.LSTM后输出大小的featu ...
【OCR】CTC loss原理
1 CTC loss出现的背景在图像文本识别.语言识别的应用中,所面临的一个问题是神经网络输出与ground truth的长度不一致,这样一来,loss就会很难计算,举个例子来讲,如果网络的输出是& ...
『OCR_recognition』CTC loss几种解码方式
文章目录前言一.贪心搜索 (greedy search) 1.1 原理解释 1.2 图示说明 1.3 代码实现二.束搜索(Beam Search) 2.1 原理解释 2.2 图示说明 2.3 代 ...
10万元奖金语音识别赛进行中！CTC 模型 Baseline 助你轻松上分
随着互联网.智能硬件的普及,智能音箱和语音助手已经深入人们的日常生活,家居场景下的语音识别技术已成为企业和研究机构竞相追逐的关键技术. 目前,由北京智源人工智能研究院.爱数智慧.biendata 共同 ...
分享本周所学——人工智能语音识别模型CTC、RNN-T、LAS详解
本人是一名人工智能初学者,最近一周学了一下AI语音识别的原理和三种比较早期的语音识别的人工智能模型,就想把自己学到的这些东西都分享给大家,一方面想用浅显易懂的语言让大家对这几个模型有所了解,另一方面也 ...

语音识别 CTC Loss